《第4章 对圆的进一步认识》复习学案

《第4章 对圆的进一步认识》复习学案
【学习目标】
1、了解圆的有关概念，探索并理解垂径定理，探索并认识圆心角、弧、弦之间的相等关系的定理，探索并理解圆周角和圆心角的关系定理．
2、探索并理解点和圆、直线与圆以及圆与圆的位置关系：了解切线的概念，探索切线与过切点的直径之间的关系，能判定一条直线是否为圆的切线，会过圆上一点画圆的切线．
3、熟练掌握弧长和扇形面积公式及其它们的应用；理解圆锥的侧面展开图并熟练掌握圆锥的侧面积和全面积的计算．
【重难点】
重点：1、垂径定理；2、与圆有关的位置关系；3、弧长公式与扇形面积公式的应用．
难点：1、垂径定理；2、切线的性质与判定．
【知识网络】
【典例解析】
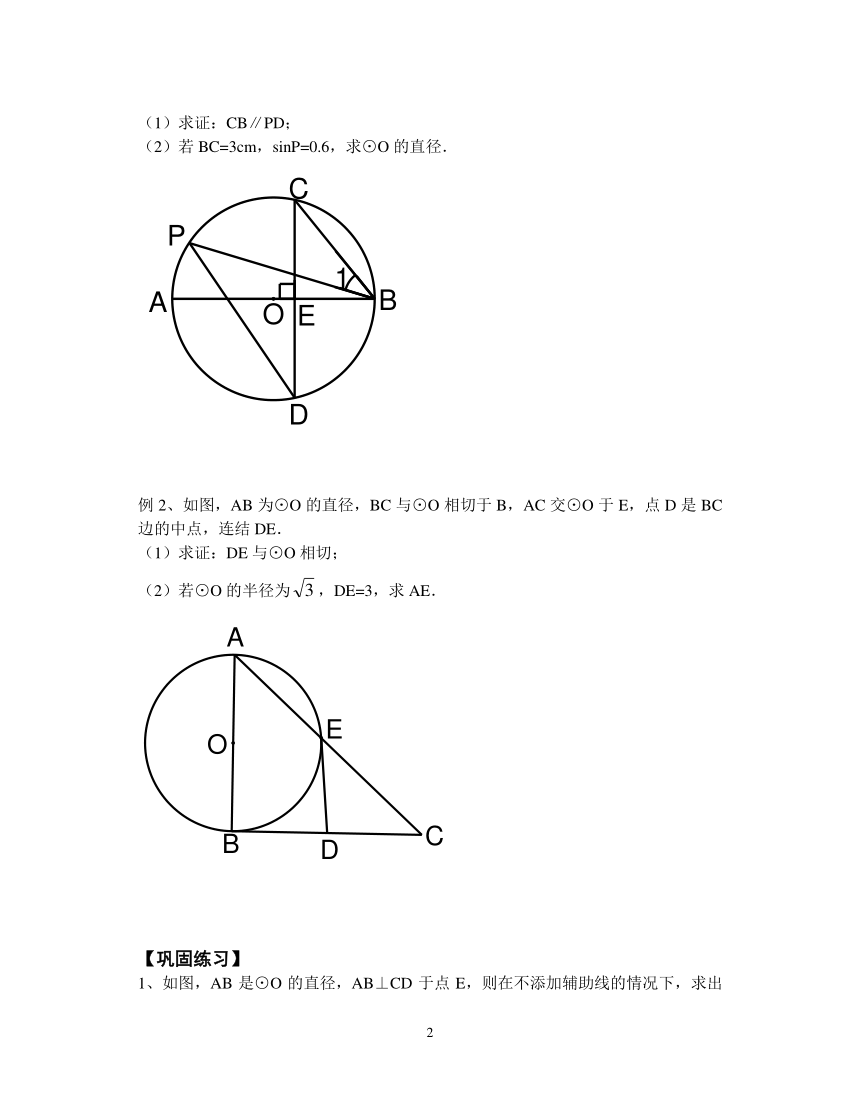
例1、如图，AB是⊙O的直径，弦CD⊥AB于点E，点P在⊙O上，∠1=∠C．
（1）求证：CB∥PD；
（2）若BC=3cm，sinP=0.6，求⊙O的直径．
例2、如图，AB为⊙O的直径，BC与⊙O相切于B，AC交⊙O于E，点D是BC边的中点，连结DE．
（1）求证：DE与⊙O相切；
（2）若⊙O的半径为，DE=3，求AE．
【巩固练习】
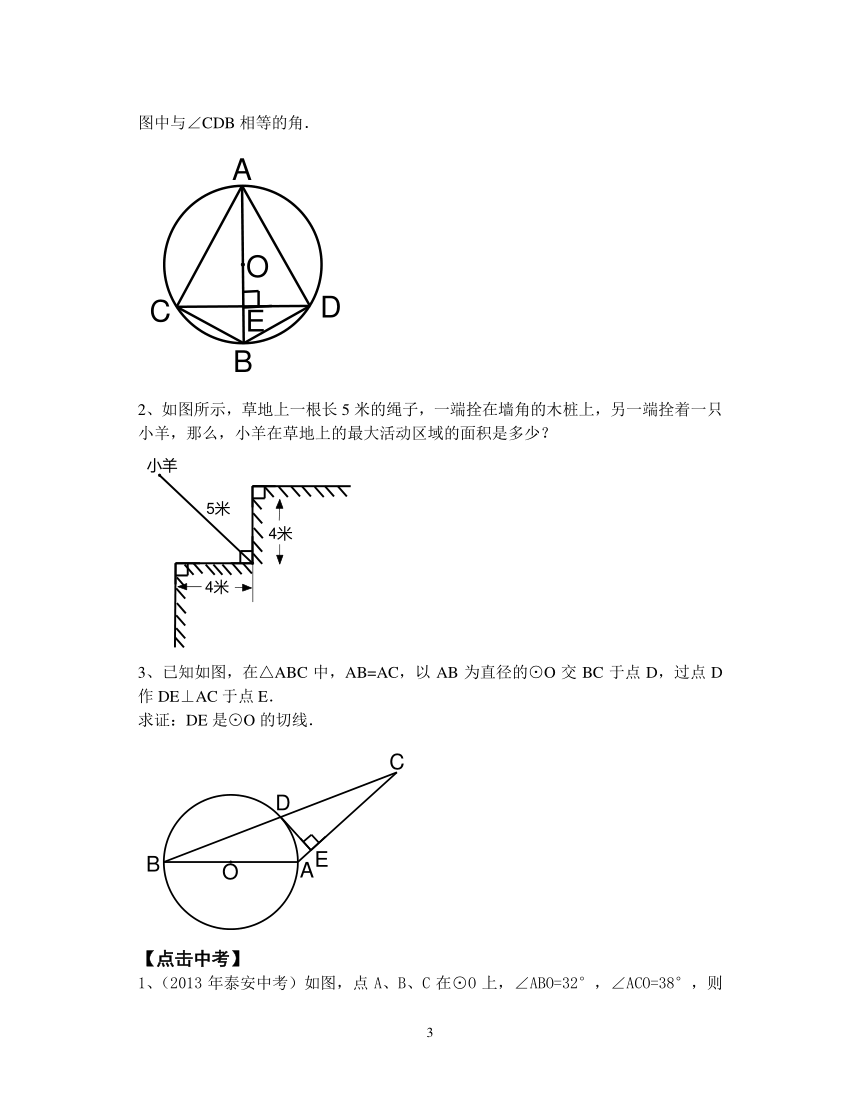
1、如图，AB是⊙O的直径，AB⊥CD于点E，则在不添加辅助线的情况下，求出图中与∠CDB相等的角．
2、如图所示，草地上一根长5米的绳子，一端拴在墙角的木桩上，另一端拴着一只小羊，那么，小羊在草地上的最大活动区域的面积是多少？
3、已知如图，在△ABC中，AB=AC，以AB为直径的⊙O交BC于点D，过点D作DE⊥AC于点E．
求证：DE是⊙O的切线．
【点击中考】
1、（2013年泰安中考）如图，点A、B、C在⊙O上，∠ABO=32°，∠ACO=38°，则∠BOC等于（ ）．
（A）60° （B）70° （C）120° （D）140°
2、（2013年泰安中考）如图，已知AB是⊙O的直径，AD切⊙O于点A，点C是的中点，则下列结论不成立的是（ ）．
（A）OC∥AE （B）EC=BC （C）∠DAE=∠ABE （D）AC⊥OE
【布置作业】
1、如图，⊙O的弦AB＝8，M是AB的中点，且OM＝3，则⊙O的半径等于（ ）
（A）8 （B）2 （C）10 （D）5
2、如图，∠AOB=100°，点C在⊙O上，且点C不与A，B重合，则∠ACB的度数为（ ）
（A）50° （B）50°或80° （C）130° （D）50°或130°
3、已知两圆的半径分别为3和7，且这两圆有公共点，则这两圆的圆心距d为（ ）
（A）4 （B）10 （C）4或10 （D）4《d《10
4、如图，⊙O是△ABC的外接圆，CD是直径，∠B＝40°，则∠ACD的度数是　　　．
5、如图，以O为圆心的两个同心圆中，大圆的弦AB是小圆的切线，C为切点。若两圆的半径分别为3cm和5cm，则AB的长为______cm．
6、如图，点C、D分别在扇形AOB的半径OA、OB的延长线上，且OA＝3，AC＝2，CD平行于AB，并与弧AB相交于点M、N．
（1）求线段OD的长；
（2）若，求弦MN的长．
弧长和扇形面积的计算
三角形的内切圆
三角形的外接圆
圆与圆的位置关系
直线与圆的位置关系
点与圆的位置关系
圆周角定理
圆心角、弧、弦
之间的关系定理
中心对称
垂径定理
轴对称
与圆有关的角的性质
圆的对称性
圆中的计算
三角形与圆
与圆有关的位置关系
圆的基本性质
圆
PAGE
6