专题2 尺规分析作图(含答案)- 2023年中考数学二轮专题复习
文档属性
| 名称 | 专题2 尺规分析作图(含答案)- 2023年中考数学二轮专题复习 |  | |
| 格式 | docx | ||
| 文件大小 | 638.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-11 17:42:33 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
专题2尺规分析作图
专题价值
尺规分析作图,是初中阶段几何的一个难点.它以五种基本作图为基础,结合许多定理性质,考查学生的几何综合素养.最近几年,各地中考中也多有涉及.我们在解题时,要认真分析题目中的已知条件,挖掘问题背后所考查的到底是什么知识点,许多问题就可以顺利解决.
常用解题思路
1.作一条线段等于已知线段;
已知线段,求作线段,使.
作法:
(1)作射线.
(2)在射线上截取,线段即为所求.
2.作一个角等于已知角;
已知,求作,使.
作法:
(1)作射线.
(2)以点为圆心,适当长为半径画弧,交于点,交于点.
(3)以点为圆心,长为半径画弧,交于点.
(4)以点为圆心,长为半径画弧,交(3)所作的弧于点.
(5)过点作射线即为所求.
3.作已知线段的垂直平分线;
已知线段,求作线段的垂直平分线.
作法:
(1)分别以为圆心,以大于一半的长为半径在两侧画弧,分别交于两点.
(2)作直线,即为所求.
4.作已知角的角平分线;
已知,求作内部射线,使.
作法:
(1)以点为圆心,适当长为半径画弧,交于点,交于点.
(2)分别以为圆心,大于一半的长为半径作弧,交内部一点.
(3)作射线,即为所求.
5.过一点作已知直线的垂线(直线上).
已知直线、及直线上一点,求作直线经过点,且.
作法:
(1)以点为圆心,适当长为半径画弧,交于两点.
(2)以点为圆心,以大于一半的长为半径画弧.
(3)以点为圆心,以大于一半的长为半径画弧,与(2)中所作的弧的交点记为点.
(4)经过点作直线,即为所求.
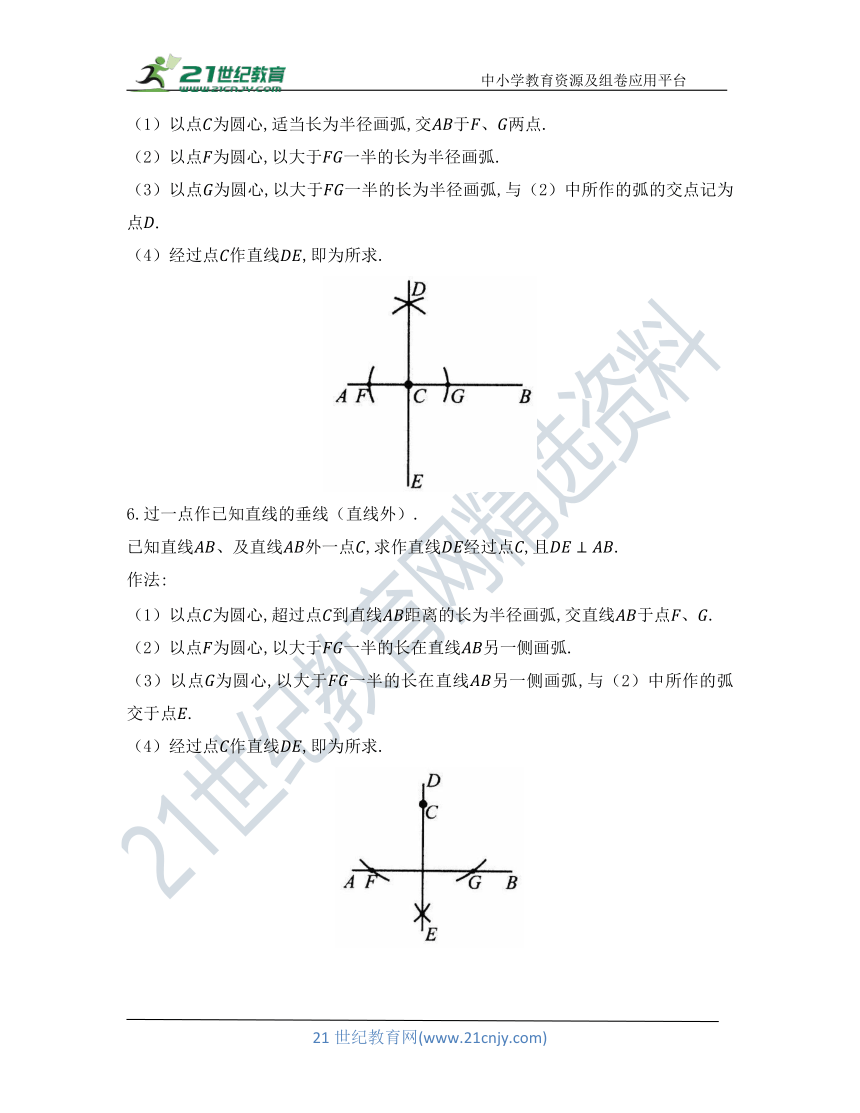
6.过一点作已知直线的垂线(直线外).
已知直线、及直线外一点,求作直线经过点,且.
作法:
(1)以点为圆心,超过点到直线距离的长为半径画弧,交直线于点.
(2)以点为圆心,以大于一半的长在直线另一侧画弧.
(3)以点为圆心,以大于一半的长在直线另一侧画弧,与(2)中所作的弧交于点.
(4)经过点作直线,即为所求.
曾经这么考!
一、结合勾股定理构造无理数
例1(1)如图1,Rt中,.现以为圆心、为半径画弧交边于,再以为圆心,长为半径画弧交边于.
求证:.(这个比值叫做与的黄金比.)
图1
(2)如果一等腰三角形的底边与腰的比等于黄金比,那么这个等腰三角形就叫做黄金三角形.请以图2中的线段为腰,用直尺和圆规,作一个黄金三角形.(注:直尺没有刻度!作图不要求写作法,但要保留作图痕迹,并对作图中涉及的点用字母进行标注.)
图2
【剖析】
(1)可以设,分别用含的代数式表示出的长,进而得出的长,则与之比可求.
(2)在图1的基础上,保证新作的长等于原来的长,长等于原来的长即可,实际操作时,分别以为圆心,长为半径作圆,以为圆心,原长为半径作圆,两圆交点即为.但在构造长的一半,作时,要用到基本作图(3),(5).
【解答】
(1)证明:Rt中,设,则,
.
(2)作的中垂线,确定的中点.
过点作的垂线,以为圆心,长为半径作弧,交所作垂线于点.
连接,以点为圆心,长为半径作弧,交于.
以点为圆心,长为半径作弧.
以点为圆心,长为半径作弧.两弧交于点,连接、即为所求.
二、利用线段成比例构造平行
例2如图,,以点为圆心1为半径画与的延长线交于点,过点画的垂线,垂线与的一个交点为,连.
(1)线段的长等于________.
(2)请在图中按下列要求逐一操作,并回答问题.
①以点_________为圆心、以线段________的长为半径画弧,与射线交于点,使线段的长等于;
②连,在上画出点,使的长等于,请写出画法,并说明理由.
【剖析】
(1)由圆的半径为1,可得出,在中利用勾股定理即可得出长;
(2)①由点在射线上,且,可知点在下方,在中,知道了长,长,可利用勾股定理求出的长度,从而确定点的位置,根据画图的步骤,找到圆心,确定半径长,在射线上截取点即可;
②由长是长的三分之二,可知点是上靠近点的三等分点,结合,可知点是上靠近点的三等分点,联想到平行线分线段成比例定理,则过点作的平行线,与的交点即为点.
【解答】
(1)在Rt中,.
(2)(1)在Rt中,,
.
如图1,以点为圆心,以线段的长为半径画弧,与射线交于点,使线段的长等于
图1 图2
(2),.
故作法如下:
如图2,连接,过点作交于点点即为所求.
三、借助图形性质构造对称
例3如图,平面直角坐标系中,已知点的坐标为.
(1)请用直尺(不带刻度)和圆规作一条直线,它与轴和轴的正半轴分别交于点和点,且使与的面积相等.(作图不必写作法,但要保留作图痕迹.)
(2)问:(1)中这样的直线是否唯一 若唯一,请说明理由;若不唯一,请在图中画出所有这样的直线,并写出与之对应的函数表达式.
【剖析】
(1)显然,要保证两个以公共边作为斜边的直角三角形面积相等,则斜边上的高也相等,根据等积法,两条直角边的乘积也相等,而两条直角边的平方和也都等于的平方,利用完全平方公式可知,这两个直角三角形的直角边必然对应相等,则这两个直角三角形必然全等.
因此,若,则两个三角形成中心对称.作矩形,作对角线,满足条件;若,则两个三角形成轴对称.作线段的垂直平分线,满足条件.
(2)分别求出点,点的坐标,即可求出函数表达式;
【解答】
(1)如图1,图2,即为所求.
图1 图2 图3
(2)①当与成中心对称时,如图1可得点坐标为,点坐标为,设,把代入得,.
②当与成轴对称时,如图3,过点作轴于,过点作交延长线于点.
设,Rt中,,
,
设,Rt中,,
,
设,把代入得,,
综上,函数表达式为或.
四、借助图形变化,将非共线线段转化
例4如图,在Rt中,,点是的中点,.
(1)试用无刻度的直尺和圆规,在上作一点,使得直线平分Rt的周长;(不要求写作法,但要保留作图痕迹).
(2)在(1)的条件下,若分Rt面积为两部分,请探究与的数量关系.
【剖析】
(1)由于点为中点,则,要使得平分Rt的周长,则要平分的长,可以考虑将转化到同一直线上,拼成一条线段,作出这条线段的中垂线即可.则可将绕点顺时针旋转到,作的中垂线交于点即可.
(2)显然,若连接,则面积为面积的一半,面积小于面积,则,可设,建立关于的方程求解.
【解答】
(1)如图1,点即为所求.
图1 图2
(2)设,如图2,作于,则.
还会怎么考
1.如图,为上一点,请用直尺(不带刻度)和圆规作出的内接正方形;不要求写作法,但要保留作图痕迹.
第1题图
2.如图,已知,请根据“”基本事实作出,使.(只保留作图痕迹,不要求写出作法)
第2题图
3.如图,已知:在中,.
(1)求作:的外接圆.(要求:尺规作图,保留作图痕迹,不写作法)
(2)若的外接圆的圆心到边的距离为,则_________.
第3题图
4.如图,已知在中,.
(1)请用圆规和直尺作出,使圆心在边上,且与两边都相切(保留作图痕迹,不写作法和证明).
(2)在(1)的条件下,若切于点,求劣弧的长.
第4题图
5.如图,在中,,点在上.
(1)求作:,使点在上,且(要求:尺规作图,保留作图痕迹,不写作法)
(2)在的条件下,若,求证:.
第5题图
6.在Rt中,.
(1)如图1,点在斜边上,以点为圆心,长为半径的圆交于点,交于点,与边相切于点.求证:;
(2)在图2中作,使它满足以下条件:
①圆心在边上;②经过点;③与边相切.
(尺规作图,只保留作图痕迹,不要求写出作法)
图1 图2
第6题图
7.如图,已知,请用无刻度直尺和圆规(不要求写作法,但要保留作图痕迹).在边上找一点,使得:将沿着过点的某一条直线折叠,点能落在边上的点处,且,请在图中作出点.
第7题图
8.如图,已知,请用直尺(不带刻度)和圆规,按下列要求作图(不要求写作法,但要保留作图痕迹):
(1)在边上确定一点,使得;
(2)作出一个,使得:①是直角三角形;②的周长等于边的长.
第8题图
【回归课本】
我们曾学习过一个基本事实:两条直线被一组平行线所截,所得的对应线段成比例.
【初步体验】
(1)如图1,在中,点在上,在上,.
若,则________,________
图1 图2
(2)如图2,在中,点在上,在上,且.以为边构造(即;以为边构造(即).
求证:.
【深入探究】
上述基本事实启发我们可以用“平行线分线段成比例”解决下列问题:
(3)如图3,已知和线段,请用直尺与圆规作.
满足:(1);(2)的周长等于线段的长度.(保留作图痕迹,并写出作图步骤)
图3
10.如图,已知矩形是上一点.
(1)利用尺规分别在上确定点,使得四边形是特殊的平行四边形;(提示:(1)保留作图痕迹,不写作法;(2)只需作出一种情况即可.)
(2)在(1)的条件下,若,则所作四边形的周长为____________.
第10题图
11.如图,已知矩形,点为线段上任一点.
(1)若,请在下图中用尺规作图画出符合要求的点;(保留作图痕迹,不要求写做法)
(2)若符合(1)中要求的点必定存在,求的取值范围.
第11题图
12.如图,等腰直角中,,请用直尺与圆规,作出符合下列条件的各点,不写作法,但保留必要的作图痕迹.
(1)作上一点上一点,使得,且最大.
(2)在第一问的条件下,作上一点上一点,使得,且最小,并直接写出这个最小值.
第12题图
专题2尺规分析作图
1.如图,连接并延长交于点,作的中垂线交于点,四边形即为所求.
第1题图
2.如图,作,在的两边分别截取,连接即为所求.
第2题图
3.(1)如图,分别作线段的垂直平分线,交于点,以为圆心,为半径作,即为所求.(2)设线段的垂直平分线交于点.由题意得,,在Rt中,.
第3题图
4.(1)作的角平分线交于点,以点为圆心,为半径作圆.
(2)连接,易证
第4题图
5.(1),故作即可,如图即为所求.
(2),
.
第5题图
6.(1)证明:如图1,连接,
是的切线,,
.
(2)如图2,作的平分线交于点,作的垂直平分线交于,以为圆心,为半径作圆,即为所求.
第6题图1
第6题图2
7.方法1:
如图1,过点作交延长线于点,作的平分线交于.
原理:角平分线上的点到角两边的距离相等.
方法2:
如图2,过点作于点,作的平分线交于,作的中垂线交于.原理:平行加角平分构造等腰三角形.
第7题图1
第7题图2
8.(1)如图1,作的垂直平分线交于点,点即为所求;
(2)如图2,在上取点,过点作的垂线,在垂线上取点使,连接,作的垂直平分线交于点,连接即为所求.
第8题图1
第8题图2
9.(1)3,2;(2)证明,,
.
(3)第一步:作射线,在射线上截取,
第二步:在射线上截取,连接,作,
第三步:截取,将点看作点,则即为所求.
第9题图
10.(1)如图1,可作一种菱形,如图2,图3,可作两种矩形.
第10题图1
第10题图2
第10题图3
(2)(1)如图1,设,易知,所作四边形的周长为.
(2)如图2,易证,
,所作四边形的周长为.
(3)如图3,易证,
,
所作四边形的周长为.
11.(1)如图1,以为边分别作等边三角形,交于点,以点为圆心,为半径作圆,交于点和,就是符合要求的点,作为圆心角,则为圆周角,是.
第11题图1
第11题图2
第11题图3
(2)如图2,当点和与点,点分别重合时,,
.
如图3,当与相切时,只有一个这样的点,连接并延长,交于,易证.
12.(1)要使最大,则最小,由垂线段最短可知,要满足,由于是等腰直角三角形,三线合一.如图1,作的角平分线,与交于点,以为圆心,长为半径画弧,交延长线于.以为圆心,长为半径画弧,与交点即为点.
第12题图1
第12题图2
第12题图3
(2)法1:如图2,过点作的平行线,在平行线上取点使得,易证,最小值为.
法2:如图3,连接,由(1)得,,即易证,最小值为.
21世纪教育网(www.21cnjy.com)
专题2尺规分析作图
专题价值
尺规分析作图,是初中阶段几何的一个难点.它以五种基本作图为基础,结合许多定理性质,考查学生的几何综合素养.最近几年,各地中考中也多有涉及.我们在解题时,要认真分析题目中的已知条件,挖掘问题背后所考查的到底是什么知识点,许多问题就可以顺利解决.
常用解题思路
1.作一条线段等于已知线段;
已知线段,求作线段,使.
作法:
(1)作射线.
(2)在射线上截取,线段即为所求.
2.作一个角等于已知角;
已知,求作,使.
作法:
(1)作射线.
(2)以点为圆心,适当长为半径画弧,交于点,交于点.
(3)以点为圆心,长为半径画弧,交于点.
(4)以点为圆心,长为半径画弧,交(3)所作的弧于点.
(5)过点作射线即为所求.
3.作已知线段的垂直平分线;
已知线段,求作线段的垂直平分线.
作法:
(1)分别以为圆心,以大于一半的长为半径在两侧画弧,分别交于两点.
(2)作直线,即为所求.
4.作已知角的角平分线;
已知,求作内部射线,使.
作法:
(1)以点为圆心,适当长为半径画弧,交于点,交于点.
(2)分别以为圆心,大于一半的长为半径作弧,交内部一点.
(3)作射线,即为所求.
5.过一点作已知直线的垂线(直线上).
已知直线、及直线上一点,求作直线经过点,且.
作法:
(1)以点为圆心,适当长为半径画弧,交于两点.
(2)以点为圆心,以大于一半的长为半径画弧.
(3)以点为圆心,以大于一半的长为半径画弧,与(2)中所作的弧的交点记为点.
(4)经过点作直线,即为所求.
6.过一点作已知直线的垂线(直线外).
已知直线、及直线外一点,求作直线经过点,且.
作法:
(1)以点为圆心,超过点到直线距离的长为半径画弧,交直线于点.
(2)以点为圆心,以大于一半的长在直线另一侧画弧.
(3)以点为圆心,以大于一半的长在直线另一侧画弧,与(2)中所作的弧交于点.
(4)经过点作直线,即为所求.
曾经这么考!
一、结合勾股定理构造无理数
例1(1)如图1,Rt中,.现以为圆心、为半径画弧交边于,再以为圆心,长为半径画弧交边于.
求证:.(这个比值叫做与的黄金比.)
图1
(2)如果一等腰三角形的底边与腰的比等于黄金比,那么这个等腰三角形就叫做黄金三角形.请以图2中的线段为腰,用直尺和圆规,作一个黄金三角形.(注:直尺没有刻度!作图不要求写作法,但要保留作图痕迹,并对作图中涉及的点用字母进行标注.)
图2
【剖析】
(1)可以设,分别用含的代数式表示出的长,进而得出的长,则与之比可求.
(2)在图1的基础上,保证新作的长等于原来的长,长等于原来的长即可,实际操作时,分别以为圆心,长为半径作圆,以为圆心,原长为半径作圆,两圆交点即为.但在构造长的一半,作时,要用到基本作图(3),(5).
【解答】
(1)证明:Rt中,设,则,
.
(2)作的中垂线,确定的中点.
过点作的垂线,以为圆心,长为半径作弧,交所作垂线于点.
连接,以点为圆心,长为半径作弧,交于.
以点为圆心,长为半径作弧.
以点为圆心,长为半径作弧.两弧交于点,连接、即为所求.
二、利用线段成比例构造平行
例2如图,,以点为圆心1为半径画与的延长线交于点,过点画的垂线,垂线与的一个交点为,连.
(1)线段的长等于________.
(2)请在图中按下列要求逐一操作,并回答问题.
①以点_________为圆心、以线段________的长为半径画弧,与射线交于点,使线段的长等于;
②连,在上画出点,使的长等于,请写出画法,并说明理由.
【剖析】
(1)由圆的半径为1,可得出,在中利用勾股定理即可得出长;
(2)①由点在射线上,且,可知点在下方,在中,知道了长,长,可利用勾股定理求出的长度,从而确定点的位置,根据画图的步骤,找到圆心,确定半径长,在射线上截取点即可;
②由长是长的三分之二,可知点是上靠近点的三等分点,结合,可知点是上靠近点的三等分点,联想到平行线分线段成比例定理,则过点作的平行线,与的交点即为点.
【解答】
(1)在Rt中,.
(2)(1)在Rt中,,
.
如图1,以点为圆心,以线段的长为半径画弧,与射线交于点,使线段的长等于
图1 图2
(2),.
故作法如下:
如图2,连接,过点作交于点点即为所求.
三、借助图形性质构造对称
例3如图,平面直角坐标系中,已知点的坐标为.
(1)请用直尺(不带刻度)和圆规作一条直线,它与轴和轴的正半轴分别交于点和点,且使与的面积相等.(作图不必写作法,但要保留作图痕迹.)
(2)问:(1)中这样的直线是否唯一 若唯一,请说明理由;若不唯一,请在图中画出所有这样的直线,并写出与之对应的函数表达式.
【剖析】
(1)显然,要保证两个以公共边作为斜边的直角三角形面积相等,则斜边上的高也相等,根据等积法,两条直角边的乘积也相等,而两条直角边的平方和也都等于的平方,利用完全平方公式可知,这两个直角三角形的直角边必然对应相等,则这两个直角三角形必然全等.
因此,若,则两个三角形成中心对称.作矩形,作对角线,满足条件;若,则两个三角形成轴对称.作线段的垂直平分线,满足条件.
(2)分别求出点,点的坐标,即可求出函数表达式;
【解答】
(1)如图1,图2,即为所求.
图1 图2 图3
(2)①当与成中心对称时,如图1可得点坐标为,点坐标为,设,把代入得,.
②当与成轴对称时,如图3,过点作轴于,过点作交延长线于点.
设,Rt中,,
,
设,Rt中,,
,
设,把代入得,,
综上,函数表达式为或.
四、借助图形变化,将非共线线段转化
例4如图,在Rt中,,点是的中点,.
(1)试用无刻度的直尺和圆规,在上作一点,使得直线平分Rt的周长;(不要求写作法,但要保留作图痕迹).
(2)在(1)的条件下,若分Rt面积为两部分,请探究与的数量关系.
【剖析】
(1)由于点为中点,则,要使得平分Rt的周长,则要平分的长,可以考虑将转化到同一直线上,拼成一条线段,作出这条线段的中垂线即可.则可将绕点顺时针旋转到,作的中垂线交于点即可.
(2)显然,若连接,则面积为面积的一半,面积小于面积,则,可设,建立关于的方程求解.
【解答】
(1)如图1,点即为所求.
图1 图2
(2)设,如图2,作于,则.
还会怎么考
1.如图,为上一点,请用直尺(不带刻度)和圆规作出的内接正方形;不要求写作法,但要保留作图痕迹.
第1题图
2.如图,已知,请根据“”基本事实作出,使.(只保留作图痕迹,不要求写出作法)
第2题图
3.如图,已知:在中,.
(1)求作:的外接圆.(要求:尺规作图,保留作图痕迹,不写作法)
(2)若的外接圆的圆心到边的距离为,则_________.
第3题图
4.如图,已知在中,.
(1)请用圆规和直尺作出,使圆心在边上,且与两边都相切(保留作图痕迹,不写作法和证明).
(2)在(1)的条件下,若切于点,求劣弧的长.
第4题图
5.如图,在中,,点在上.
(1)求作:,使点在上,且(要求:尺规作图,保留作图痕迹,不写作法)
(2)在的条件下,若,求证:.
第5题图
6.在Rt中,.
(1)如图1,点在斜边上,以点为圆心,长为半径的圆交于点,交于点,与边相切于点.求证:;
(2)在图2中作,使它满足以下条件:
①圆心在边上;②经过点;③与边相切.
(尺规作图,只保留作图痕迹,不要求写出作法)
图1 图2
第6题图
7.如图,已知,请用无刻度直尺和圆规(不要求写作法,但要保留作图痕迹).在边上找一点,使得:将沿着过点的某一条直线折叠,点能落在边上的点处,且,请在图中作出点.
第7题图
8.如图,已知,请用直尺(不带刻度)和圆规,按下列要求作图(不要求写作法,但要保留作图痕迹):
(1)在边上确定一点,使得;
(2)作出一个,使得:①是直角三角形;②的周长等于边的长.
第8题图
【回归课本】
我们曾学习过一个基本事实:两条直线被一组平行线所截,所得的对应线段成比例.
【初步体验】
(1)如图1,在中,点在上,在上,.
若,则________,________
图1 图2
(2)如图2,在中,点在上,在上,且.以为边构造(即;以为边构造(即).
求证:.
【深入探究】
上述基本事实启发我们可以用“平行线分线段成比例”解决下列问题:
(3)如图3,已知和线段,请用直尺与圆规作.
满足:(1);(2)的周长等于线段的长度.(保留作图痕迹,并写出作图步骤)
图3
10.如图,已知矩形是上一点.
(1)利用尺规分别在上确定点,使得四边形是特殊的平行四边形;(提示:(1)保留作图痕迹,不写作法;(2)只需作出一种情况即可.)
(2)在(1)的条件下,若,则所作四边形的周长为____________.
第10题图
11.如图,已知矩形,点为线段上任一点.
(1)若,请在下图中用尺规作图画出符合要求的点;(保留作图痕迹,不要求写做法)
(2)若符合(1)中要求的点必定存在,求的取值范围.
第11题图
12.如图,等腰直角中,,请用直尺与圆规,作出符合下列条件的各点,不写作法,但保留必要的作图痕迹.
(1)作上一点上一点,使得,且最大.
(2)在第一问的条件下,作上一点上一点,使得,且最小,并直接写出这个最小值.
第12题图
专题2尺规分析作图
1.如图,连接并延长交于点,作的中垂线交于点,四边形即为所求.
第1题图
2.如图,作,在的两边分别截取,连接即为所求.
第2题图
3.(1)如图,分别作线段的垂直平分线,交于点,以为圆心,为半径作,即为所求.(2)设线段的垂直平分线交于点.由题意得,,在Rt中,.
第3题图
4.(1)作的角平分线交于点,以点为圆心,为半径作圆.
(2)连接,易证
第4题图
5.(1),故作即可,如图即为所求.
(2),
.
第5题图
6.(1)证明:如图1,连接,
是的切线,,
.
(2)如图2,作的平分线交于点,作的垂直平分线交于,以为圆心,为半径作圆,即为所求.
第6题图1
第6题图2
7.方法1:
如图1,过点作交延长线于点,作的平分线交于.
原理:角平分线上的点到角两边的距离相等.
方法2:
如图2,过点作于点,作的平分线交于,作的中垂线交于.原理:平行加角平分构造等腰三角形.
第7题图1
第7题图2
8.(1)如图1,作的垂直平分线交于点,点即为所求;
(2)如图2,在上取点,过点作的垂线,在垂线上取点使,连接,作的垂直平分线交于点,连接即为所求.
第8题图1
第8题图2
9.(1)3,2;(2)证明,,
.
(3)第一步:作射线,在射线上截取,
第二步:在射线上截取,连接,作,
第三步:截取,将点看作点,则即为所求.
第9题图
10.(1)如图1,可作一种菱形,如图2,图3,可作两种矩形.
第10题图1
第10题图2
第10题图3
(2)(1)如图1,设,易知,所作四边形的周长为.
(2)如图2,易证,
,所作四边形的周长为.
(3)如图3,易证,
,
所作四边形的周长为.
11.(1)如图1,以为边分别作等边三角形,交于点,以点为圆心,为半径作圆,交于点和,就是符合要求的点,作为圆心角,则为圆周角,是.
第11题图1
第11题图2
第11题图3
(2)如图2,当点和与点,点分别重合时,,
.
如图3,当与相切时,只有一个这样的点,连接并延长,交于,易证.
12.(1)要使最大,则最小,由垂线段最短可知,要满足,由于是等腰直角三角形,三线合一.如图1,作的角平分线,与交于点,以为圆心,长为半径画弧,交延长线于.以为圆心,长为半径画弧,与交点即为点.
第12题图1
第12题图2
第12题图3
(2)法1:如图2,过点作的平行线,在平行线上取点使得,易证,最小值为.
法2:如图3,连接,由(1)得,,即易证,最小值为.
21世纪教育网(www.21cnjy.com)
同课章节目录
