广东省湛江市雷州市三校2023届九年级下册第一次月考数学试卷(pdf版含解析)
文档属性
| 名称 | 广东省湛江市雷州市三校2023届九年级下册第一次月考数学试卷(pdf版含解析) |  | |
| 格式 | |||
| 文件大小 | 845.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-12 15:20:00 | ||
图片预览


文档简介
雷州市第八中学 2022-2023 学年
九年级第一次模拟考试数学试卷
考试时间:90 分钟;
一、单选题(每小题 3 分,共 30 分)
1.﹣2022的倒数是( )
A 2022 B 1 C 2022 D 1. .﹣ .﹣ .
2022 2022
2.下列计算正确的是
A 2.a2 a6 a12 B. 3a 9a2 C.2a2 3a2 5a4 D. a b 2 a 2 b 2
3.下列说法正确的是( )
A.了解一批灯泡的使用寿命,应采用抽样调查的方式
B.为了直观地介绍某款牛奶各营养成分的百分比,最适合使用的统计图是条形统计图
1
C.一个抽奖活动中,中奖概率为 ,表示抽奖 20次必有 1次中奖
20
D.“投掷一枚质地均匀的硬币一次,结果正面朝上”为必然事件
4.下列各式中,是最简二次根式的是( )
A. 2 4 B. a2 C. 27 D. 2
5.2020年,新冠肺炎疫情席卷全球,截至 2022年 5月 14日,累计确诊人数超过 520000000例,抗
击疫情成为全人类共同的战役.确诊病例“520000000”用科学记数法可表示为( )
A.5.2 109 B.5.2 108 C.52 107 D.0.52 109
6.如图,点 A、B、C都在⊙O上,若∠C=40°,则∠AOB的度数为( )
第 6题图 第 7题图 第 8题图 第 9题图
A.40° B.50° C.80° D.140°
k
7.如图,P为反比例数 y= x的图象上一点,PA⊥x轴于点 A,△PAO的面积为 6,则 k的值是( )
A.6 B.12 C. - 12 D. 6
答案第 1页,共 4页
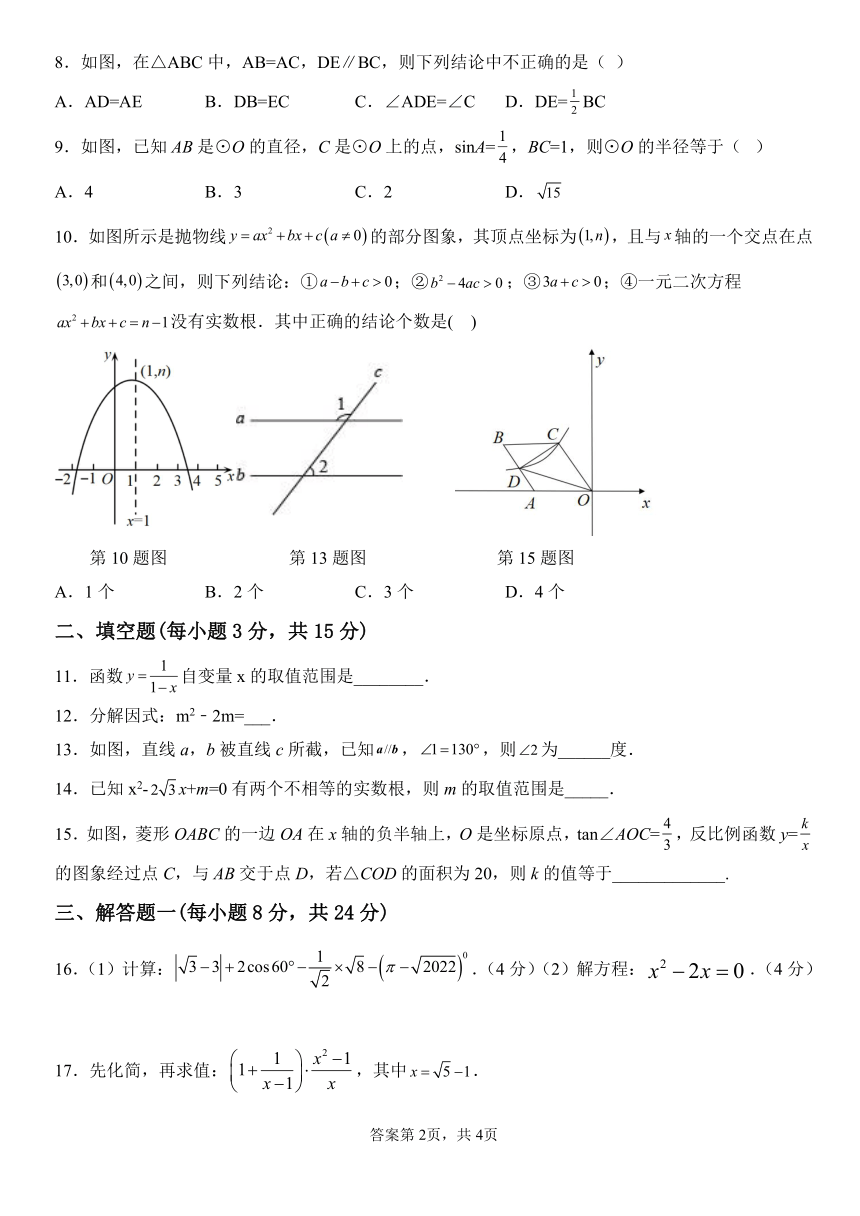
8.如图,在△ABC中,AB=AC,DE∥BC,则下列结论中不正确的是( )
A AD=AE B DB=EC C ADE= C D DE= 1. . .∠ ∠ . 2 BC
1
9.如图,已知 AB是⊙O的直径,C是⊙O上的点,sinA= ,BC=1,则⊙O的半径等于( )
4
A.4 B.3 C.2 D. 15
10 y ax2.如图所示是抛物线 bx c a 0 的部分图象,其顶点坐标为 1,n ,且与 x轴的一个交点在点
3,0 和 4,0 之间,则下列结论:①a b c 0;②b2 4ac 0;③3a c 0;④一元二次方程
ax2 bx c n 1没有实数根.其中正确的结论个数是( )
第 10题图 第 13题图 第 15题图
A.1个 B.2个 C.3个 D.4个
二、填空题(每小题 3 分,共 15 分)
1
11.函数 y 自变量 x的取值范围是________.
1 x
12.分解因式:m2﹣2m=___.
13.如图,直线 a,b被直线 c所截,已知 a //b, 1 130 ,则 2为______度.
14.已知 x2- 2 3 x+m=0有两个不相等的实数根,则 m的取值范围是_____.
4
15 k.如图,菱形 OABC的一边 OA在 x轴的负半轴上,O是坐标原点,tan∠AOC= 3,反比例函数 y= x
的图象经过点 C,与 AB交于点 D,若△COD的面积为 20,则 k的值等于_____________.
三、解答题一(每小题 8 分,共 24 分)
1 0
16.(1)计算: 3 3 2cos60 8 2022 .(4分)(2)解方程: 2
2 x 2x 0.(4分)
1 x2 117.先化简,再求值: 1 ,其中 x 5 1.
x 1 x
答案第 2页,共 4页
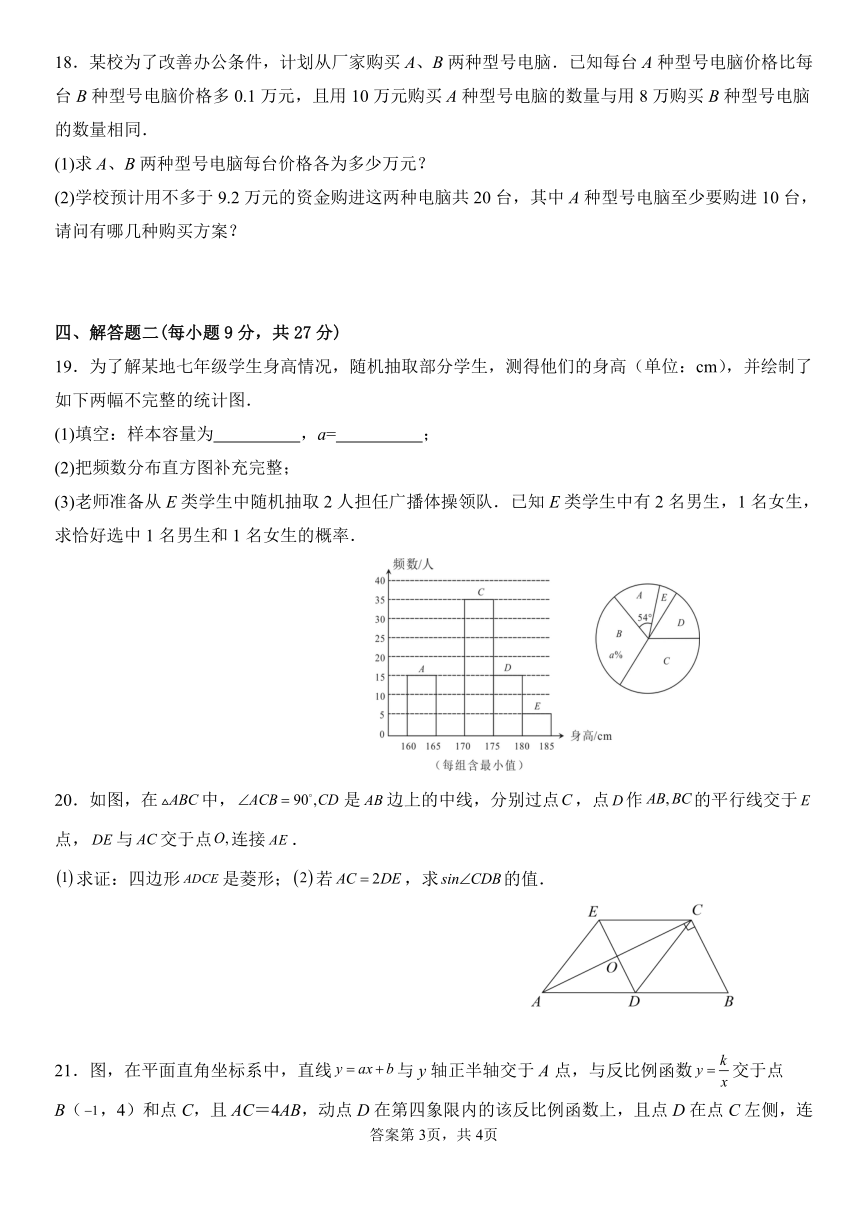
18.某校为了改善办公条件,计划从厂家购买 A、B两种型号电脑.已知每台 A种型号电脑价格比每
台 B种型号电脑价格多 0.1万元,且用 10万元购买 A种型号电脑的数量与用 8万购买 B种型号电脑
的数量相同.
(1)求 A、B两种型号电脑每台价格各为多少万元?
(2)学校预计用不多于 9.2万元的资金购进这两种电脑共 20台,其中 A种型号电脑至少要购进 10台,
请问有哪几种购买方案?
四、解答题二(每小题 9 分,共 27 分)
19.为了解某地七年级学生身高情况,随机抽取部分学生,测得他们的身高(单位:cm),并绘制了
如下两幅不完整的统计图.
(1)填空:样本容量为 ,a= ;
(2)把频数分布直方图补充完整;
(3)老师准备从 E类学生中随机抽取 2人担任广播体操领队.已知 E类学生中有 2名男生,1名女生,
求恰好选中 1名男生和 1名女生的概率.
20.如图,在 ABC中, ACB 90 ,CD 是 AB边上的中线,分别过点C,点D作 AB,BC的平行线交于 E
点,DE与 AC交于点O,连接 AE.
1 求证:四边形 ADCE是菱形; 2 若 AC 2DE,求 sin CDB的值.
21.图,在平面直角坐标系中,直线 y ax b k与 y轴正半轴交于 A点,与反比例函数 y 交于点
x
B( 1,4)和点 C,且 AC=4AB,动点 D在第四象限内的该反比例函数上,且点 D在点 C左侧,连
答案第 3页,共 4页
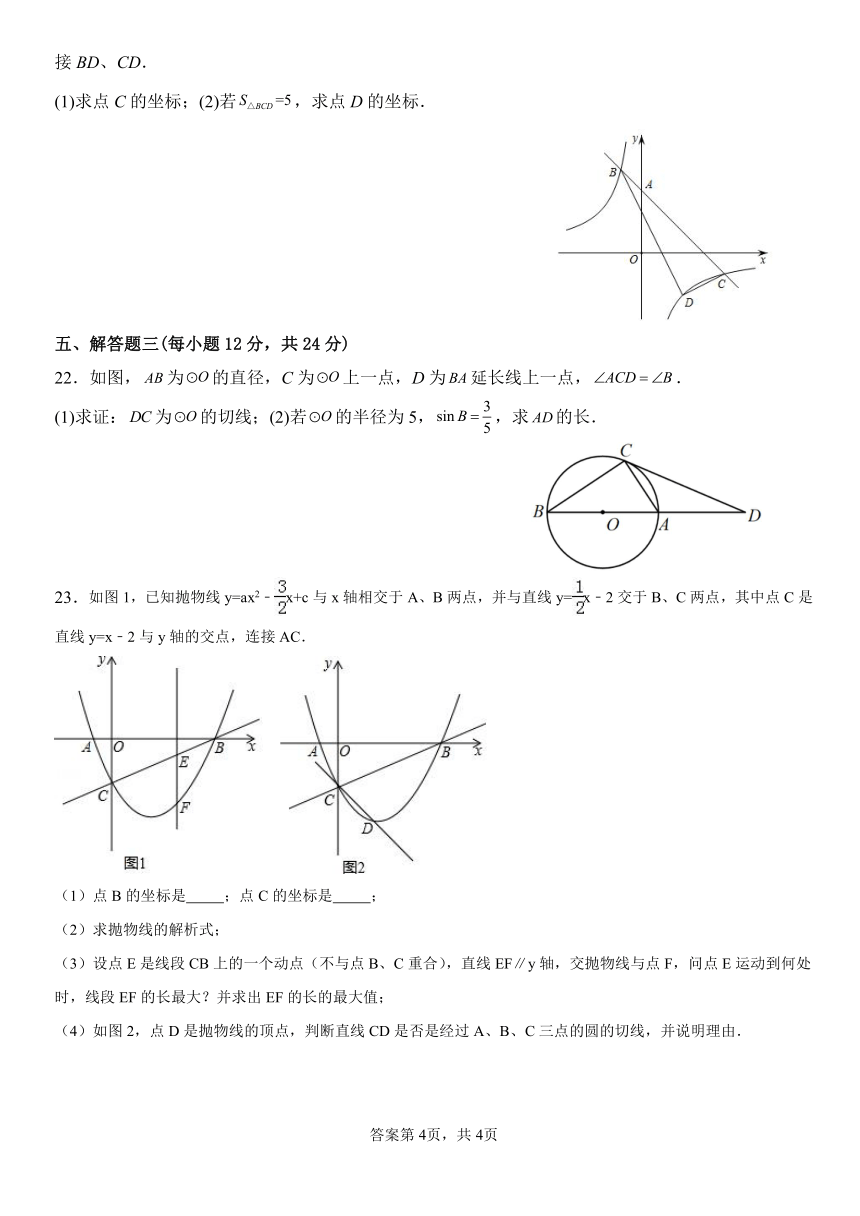
接 BD、CD.
(1)求点 C的坐标;(2)若 S△BCD =5,求点 D的坐标.
五、解答题三(每小题 12 分,共 24 分)
22.如图, AB为 O的直径,C为 O上一点,D为 BA延长线上一点, ACD B.
3
(1)求证:DC为 O的切线;(2)若 O的半径为 5, sin B ,求 AD的长.
5
23.如图 1,已知抛物线 y=ax2﹣ x+c与 x轴相交于 A、B两点,并与直线 y= x﹣2交于 B、C两点,其中点 C是
直线 y=x﹣2与 y轴的交点,连接 AC.
(1)点 B的坐标是 ;点 C的坐标是 ;
(2)求抛物线的解析式;
(3)设点 E是线段 CB上的一个动点(不与点 B、C重合),直线 EF∥y轴,交抛物线与点 F,问点 E运动到何处
时,线段 EF的长最大?并求出 EF的长的最大值;
(4)如图 2,点 D是抛物线的顶点,判断直线 CD是否是经过 A、B、C三点的圆的切线,并说明理由.
答案第 4页,共 4页
雷州市第八中学 2022-2023 学年
九年级第一次模拟考试数学试卷答案
参考答案:
1
1.B 【详解】解:﹣2022的倒数是: .
2022
故选:B.
2.B
【详解】解:A. a2 a6 a8,故该选项不正确,不符合题意;
B. 3a 2 9a2,故该选项正确,符合题意;
C. 2a2 3a2 5a2,故该选项不正确,不符合题意;
D. a b 2 a2 2ab b2,故该选项不正确,不符合题意;
故选:B.
3.A
【详解】解:A. 了解一批灯泡的使用寿命,应采用抽样调查的方式,故该选项正确,符合题意;
B. 为了直观地介绍某款牛奶各营养成分的百分比,最适合使用的统计图是扇形统计图,故该选项不正确,
不符合题意;
1
C. 一个抽奖活动中,中奖概率为 ,表示抽奖 20次可能有 1次中奖,故该选项不正确,不符合题意;
20
D. “投掷一枚质地均匀的硬币一次,结果正面朝上”为随机事件,故该选项不正确,不符合题意;
故选:A.
4.D
【详解】解:A、 2 4 2 2 2 4 2 ,不是最简二次根式,故本选项不符合题意;
B、 a2 a ,不是最简二次根式,故本选项不符合题意;
C、 27 3 3 ,不是最简二次根式,故本选项不符合题意;
D、 2是最简二次根式,故本选项符合题意;
故选:D.
5.B
【详解】解:520000000=5.2×108
故选:B.
答案第 1页,共 13页
6.C
【详解】∵∠C=40°,
∴∠AOB=2∠C=80°.
故选 C.
7.C
k
【详解】∵P为反比例数 y= 的图象上一点,PA⊥x轴于点 A,△PAO的面积为 6,
x
k
∴S△PAO= =6,
2
∵反比例函数的图象在二、四象限,
∴k<0,
∴k=-12.
故选 C.
8.D
【详解】试题分析:由 DE与 BC平行,得到△ADE∽△ABC,由相似得比例,根据 AB=AC,得到 AD=AE,
进而确定出 DB=EC,再由两直线平行同位角相等,以及等腰三角形的底角相等,等量代换得到∠ADE=∠C,
而 DE不一定为中位线,即 DE不一定为 BC的一半,即可得到正确选项.
故选 D.
考点:1、等腰三角形的判定与性质;2、平行线的性质
9.C
【详解】解:∵AB是⊙O的直径,
∴∠C=90°,
1
∵sinA= ,BC=1,
4
BC 1
∴ = ,
AB 4
∴AB=4,
∴⊙O的半径等于 2.
故选 C.
10.C
【详解】解:∵抛物线与 x轴的一个交点在点 3,0 和 4,0 之间,而抛物线的对称轴为直线 x 1,
答案第 2页,共 13页
∴抛物线与 x轴的另一个交点在点 2,0 和 1,0 之间.
∴当 x 1时, y 0,
即a b c 0,所以①正确;
∵抛物线与 x轴有两个交点,则b2 4ac 0,所以②正确;
b
∵抛物线的对称轴为直线 x 1,即b 2a,
2a
a b c 0,
a b c a 2a c 3a c 0,所以③正确;
∵抛物线与直线 y n有一个公共点,
∴由图象可得,抛物线与直线 y n 1有两个公共点,
∴一元二次方程 ax2 bx c n 1有两个实数根,所以④错误.
故选:C.
11. x 1
【详解】由题意得:1 x 0, x 1
12.m m 2 .
2
【详解】解:m 2m m m 2 .
故答案为:m m 2 .
13.50
【分析】先根据平行线的性质得出∠3=130°,再由邻补角得到∠2=50°.
【详解】解:如图,
∵ a / /b, 1 130 ,
∴∠3=130°,
又∵∠2+∠3=180°,
∴∠2=180°-∠3=180°-130°=50°.
故答案为:50.
答案第 3页,共 13页
14.m<3
【详解】解:∵x- 2 3 x+m=0有两个不相等的实数根,
∴Δ=(-2 3 )2-4m>0
解得:m<3,
故答案为: m<3.
15.﹣24
【详解】如下图,过点 C作 CF⊥AO于点 F,过点 D作 DE∥OA交 CO于点 E,设 CF=4x,
∵四边形 ABCO是菱形,
∴AB//CO,AO//BC,
∵DE//AO,
∴四边形 AOED和四边形 DECB都是平行四边形,
∴S△AOD=S△DOE,S△BCD=S△CDE,
∴S 菱形ABCD=2S△DOE+2S△CDE=2S△COD=40,
4
∵tan∠AOC= ,CF=4x,
3
∴OF=3x,
∴在 Rt△COF中,由勾股定理可得 OC=5x,
∴OA==OC=5x,
∴S 菱形ABCO=AO·CF=5x·4x=20x2=40,解得:x= 2,
∴OF=3 2,CF= 4 2,
∴点 C的坐标为 ( 3 2,4 2),
k
∵点 C在反比例函数 y 的图象上,
x
∴k= 3 2 4 2 24 .
故答案为:-24.
答案第 4页,共 13页
16.(1)1 3;(2)
1 1
【详解】解:原式=3 3 2 8 1
2 2
=3 3 1﹣2﹣1
=1 3.
16.(2). x1 0, x2 2.
【详解】解: x2 2x 0,
x x 2 0,
x 0或 x 2 0,
∴ x1 0, x2 2.
17. x 1, 5
1 x2 1
【详解】解: 1
x 1 x
x 1 1 (x 1)(x 1)
x 1 x
x x 1
x
x 1
当 x 5 1时,原式 5 1 1 5 .
答案第 5页,共 13页
18.(1)A、B两种型号电脑每台价格分别是 0.5万元和 0.4万元
(2)有 3种方案,即:购买 A种型号电脑 10台、购买 B种型号电脑 10台;购买 A种型号电脑 11台、购买
B种型号电脑 9台;购买 A种型号电脑 12台、购买 B种型号电脑 8台
【详解】(1)解:设 A种型号电脑每台价格为 x万元,则 B种型号电脑每台价格(x﹣0.1)万元.
根据题意得:
10 8
,解得 x 0.5,
x x 0.1
经检验:x=0.5是原方程的解,
x﹣0.1=0.4,
答:A、B两种型号电脑每台价格分别是 0.5万元和 0.4万元.
(2)解:设购买 A种型号电脑 y台,则购买 B种型号电脑(20﹣y)台.
根据题意得:0.5y+0.4(20﹣y)≤9.2,
解得:y≤12,
又∵A种型号电脑至少要购进 10台,
∴10≤y≤12,y的整数解为 10、11、12,
∴有 3种方案.
即:购买 A种型号电脑 10台、购买 B种型号电脑 10台;
购买 A种型号电脑 11台、购买 B种型号电脑 9台;
购买 A种型号电脑 12台、购买 B种型号电脑 8台.
19.(1)100,32;
(2)见解析;
2
(3) 3
54
【详解】(1))15÷ =100,
360
所以样本容量为 100;
B组的人数为 100-15-35-15-5=30,
30
所以 a%= ×100%=30%,则 a=30;
100
故答案为 100,30;
(2)补全频数分布直方图为:
答案第 6页,共 13页
(3)画树状图为:
4 2
共有 6种等可能的结果数,其中“1男 1女”的结果数为 4,所以恰好选中“1男 1女”的概率
6 3
sin CDB 420.(1)详见解析;(2)
5
【详解】(1)证明: CE / /BD,DE / /BC,
四边形 BDEC是平行四边形.
CE BD,
CD是 AB边上的中线,
AD BD,
CE AD,
四边形 ADCE是平行四边形.
ACB 90 ,DE / /BC,
AOD ACB 90 ,
AC DE,
四边形 ADCE是菱形.
(2)解:过点C作CF AB于 F .
答案第 7页,共 13页
平行四边形 BDEC,
DE BC,
AC 2DE,
AC 2BC,
设 BC x,
则 AC 2x,
在 Rt ACB中, ACB 90 ;
AB AC2 BC2 5x.
ACB 90 ,CF AB,
S 1 ABC AC BC
1
AB CF,
2 2
CF 2 5 x,
5
ACB 90;CD是 AB边上的中线,
CD 1 AB 5 x,
2 2
在 Rt CDF中,∠CFD 90 ,
sin CDB CF 4 .
CD 5
21.(1)C坐标为 4,-1
(2) 1 17 1 17( , )
2 2
【详解】(1)解:如图, 过点 B作 BE⊥y轴于点 E,过点 C作 CF⊥y轴于点 F
k
∵反比例函数 y 经过点 B( 1,4),
x
4 k∴ = ,
- 1
解得, k 4
答案第 8页,共 13页
4
∴反比例函数为 y
x
∵BE⊥y轴,CF⊥y轴,
∴BE∥CF,
∴△BEA∽△CFA
∵AC=4AB ,
BE AB 1
∴
CF AC 4
∴CF=4
4
∵反比例函数 y 经过点 C
x
∴当 x 4时, y 1,即点 C坐标为(4, 1)
(2)过点 D作 DG∥y轴,交 AC于点 G.
将点 B( 1,4),点 C(4, 1)代入 y ax b ,解得 a 1,b 3
∴直线的函数解析式为 y x 3
4
设点 D(t, ),点 G(t, t 3)
t
∵ S△BCD =5,
1
∴ 4 -1
-t
4
3 -
52 t
t 1 17 t 1 17解得, 1 , ,2 2 2
∵0 t 4,
t 1 17∴ 1 2
1 17 1 17
此时,点 D的坐标为( , ).
2 2
答案第 9页,共 13页
22.(1)证明见解析
90
(2)
7
【详解】(1)证明:如图所示,连接OC,
∵ AB为 O的直径,
∴ BCA 90 ,
∴∠OBC+∠OCA=90°
∵OC OB,
∴ B OCB,
又∵ ACD B,
∴ ACD OCB,
∴ OCA ACD 90 ,即 OCD 90 ,
∴DC为 O的切线;
(2)解:在Rt△ABC中, AB 10,∠ACB 90 ,sinB
3
,
5
∴ AC AB sin B 6,
∴ BC AB2 AC2 8,
∵∠ACD ∠B,∠D ∠D,
∴△ACD∽△CBD,
答案第 10页,共 13页
AC AD AD 6 3
∴ ,即 ,
BC CD CD 8 4
设 AD 3x,CD 4x ,则OD OA AD 3x 5,
在Rt△OCD中,由勾股定理得:OC2 CD 2 OD2,
52 4x 2 3x 5 2∴ ,
x 30解得 (不合题意的值舍去),
7
∴ AD 3x
90
.
7
23.(1)B(4,0),C(0,﹣2),(2)y= ;(3)E(2,﹣1),EF的最大值为 2;(4)直线
CD是经过 A、B、C三点的圆的切线,理由见解析.
解:(1)由题意知直线 y= x﹣2交 x轴、y轴于点 B、C两点,
∴B(4,0),C(0,﹣2),
(2)∵y=ax2﹣ x+c经过点 B,C,
∴ ,
解得 ,
∴y= ;
(3)如图 1:
答案第 11页,共 13页
设点 E(x, x﹣2),
∵直线 EF∥y轴,
∴点 F(x, ),
EF= x﹣2﹣( ),
EF= = ,
所以当 x=2时,EF有最大值是 2,
此时 E(2,﹣1),EF的最大值为 2;
(4)如图 2:
∵y=ax2﹣ x+c与 x轴相交于 A、B两点,
令 y=0,得 ax2﹣ x+c=0,
解得:x=﹣1,或 x=4,
∴A(﹣1,0),B(4,0),C(0,﹣2),
∴OA=1,OC=2,0B=4,
∴tan∠ACO=tan∠CBO= ,
答案第 12页,共 13页
∴∠ACO=∠CBO,
∵∠OCB+∠CBO=90°,
∴∠ACO+∠OCB=90°,
∴∠ACB=90°,
∴AB是经过 A、B、C三点的圆的直径,
设圆心 Q,则 Q( ,0),连接 QC,过点 D作 DE⊥y轴,垂足为 E,连接 QD,
y= 顶点坐标为 D( , ),
可求 CE=﹣2﹣( )= ,ED= ,CD= ,CQ= = ,QD= ,
计算得:CD2+CQ2=DQ2,
∴∠QCD=90°,
∴直线 CD是经过 A、B、C三点的圆的切线.
答案第 13页,共 13页
九年级第一次模拟考试数学试卷
考试时间:90 分钟;
一、单选题(每小题 3 分,共 30 分)
1.﹣2022的倒数是( )
A 2022 B 1 C 2022 D 1. .﹣ .﹣ .
2022 2022
2.下列计算正确的是
A 2.a2 a6 a12 B. 3a 9a2 C.2a2 3a2 5a4 D. a b 2 a 2 b 2
3.下列说法正确的是( )
A.了解一批灯泡的使用寿命,应采用抽样调查的方式
B.为了直观地介绍某款牛奶各营养成分的百分比,最适合使用的统计图是条形统计图
1
C.一个抽奖活动中,中奖概率为 ,表示抽奖 20次必有 1次中奖
20
D.“投掷一枚质地均匀的硬币一次,结果正面朝上”为必然事件
4.下列各式中,是最简二次根式的是( )
A. 2 4 B. a2 C. 27 D. 2
5.2020年,新冠肺炎疫情席卷全球,截至 2022年 5月 14日,累计确诊人数超过 520000000例,抗
击疫情成为全人类共同的战役.确诊病例“520000000”用科学记数法可表示为( )
A.5.2 109 B.5.2 108 C.52 107 D.0.52 109
6.如图,点 A、B、C都在⊙O上,若∠C=40°,则∠AOB的度数为( )
第 6题图 第 7题图 第 8题图 第 9题图
A.40° B.50° C.80° D.140°
k
7.如图,P为反比例数 y= x的图象上一点,PA⊥x轴于点 A,△PAO的面积为 6,则 k的值是( )
A.6 B.12 C. - 12 D. 6
答案第 1页,共 4页
8.如图,在△ABC中,AB=AC,DE∥BC,则下列结论中不正确的是( )
A AD=AE B DB=EC C ADE= C D DE= 1. . .∠ ∠ . 2 BC
1
9.如图,已知 AB是⊙O的直径,C是⊙O上的点,sinA= ,BC=1,则⊙O的半径等于( )
4
A.4 B.3 C.2 D. 15
10 y ax2.如图所示是抛物线 bx c a 0 的部分图象,其顶点坐标为 1,n ,且与 x轴的一个交点在点
3,0 和 4,0 之间,则下列结论:①a b c 0;②b2 4ac 0;③3a c 0;④一元二次方程
ax2 bx c n 1没有实数根.其中正确的结论个数是( )
第 10题图 第 13题图 第 15题图
A.1个 B.2个 C.3个 D.4个
二、填空题(每小题 3 分,共 15 分)
1
11.函数 y 自变量 x的取值范围是________.
1 x
12.分解因式:m2﹣2m=___.
13.如图,直线 a,b被直线 c所截,已知 a //b, 1 130 ,则 2为______度.
14.已知 x2- 2 3 x+m=0有两个不相等的实数根,则 m的取值范围是_____.
4
15 k.如图,菱形 OABC的一边 OA在 x轴的负半轴上,O是坐标原点,tan∠AOC= 3,反比例函数 y= x
的图象经过点 C,与 AB交于点 D,若△COD的面积为 20,则 k的值等于_____________.
三、解答题一(每小题 8 分,共 24 分)
1 0
16.(1)计算: 3 3 2cos60 8 2022 .(4分)(2)解方程: 2
2 x 2x 0.(4分)
1 x2 117.先化简,再求值: 1 ,其中 x 5 1.
x 1 x
答案第 2页,共 4页
18.某校为了改善办公条件,计划从厂家购买 A、B两种型号电脑.已知每台 A种型号电脑价格比每
台 B种型号电脑价格多 0.1万元,且用 10万元购买 A种型号电脑的数量与用 8万购买 B种型号电脑
的数量相同.
(1)求 A、B两种型号电脑每台价格各为多少万元?
(2)学校预计用不多于 9.2万元的资金购进这两种电脑共 20台,其中 A种型号电脑至少要购进 10台,
请问有哪几种购买方案?
四、解答题二(每小题 9 分,共 27 分)
19.为了解某地七年级学生身高情况,随机抽取部分学生,测得他们的身高(单位:cm),并绘制了
如下两幅不完整的统计图.
(1)填空:样本容量为 ,a= ;
(2)把频数分布直方图补充完整;
(3)老师准备从 E类学生中随机抽取 2人担任广播体操领队.已知 E类学生中有 2名男生,1名女生,
求恰好选中 1名男生和 1名女生的概率.
20.如图,在 ABC中, ACB 90 ,CD 是 AB边上的中线,分别过点C,点D作 AB,BC的平行线交于 E
点,DE与 AC交于点O,连接 AE.
1 求证:四边形 ADCE是菱形; 2 若 AC 2DE,求 sin CDB的值.
21.图,在平面直角坐标系中,直线 y ax b k与 y轴正半轴交于 A点,与反比例函数 y 交于点
x
B( 1,4)和点 C,且 AC=4AB,动点 D在第四象限内的该反比例函数上,且点 D在点 C左侧,连
答案第 3页,共 4页
接 BD、CD.
(1)求点 C的坐标;(2)若 S△BCD =5,求点 D的坐标.
五、解答题三(每小题 12 分,共 24 分)
22.如图, AB为 O的直径,C为 O上一点,D为 BA延长线上一点, ACD B.
3
(1)求证:DC为 O的切线;(2)若 O的半径为 5, sin B ,求 AD的长.
5
23.如图 1,已知抛物线 y=ax2﹣ x+c与 x轴相交于 A、B两点,并与直线 y= x﹣2交于 B、C两点,其中点 C是
直线 y=x﹣2与 y轴的交点,连接 AC.
(1)点 B的坐标是 ;点 C的坐标是 ;
(2)求抛物线的解析式;
(3)设点 E是线段 CB上的一个动点(不与点 B、C重合),直线 EF∥y轴,交抛物线与点 F,问点 E运动到何处
时,线段 EF的长最大?并求出 EF的长的最大值;
(4)如图 2,点 D是抛物线的顶点,判断直线 CD是否是经过 A、B、C三点的圆的切线,并说明理由.
答案第 4页,共 4页
雷州市第八中学 2022-2023 学年
九年级第一次模拟考试数学试卷答案
参考答案:
1
1.B 【详解】解:﹣2022的倒数是: .
2022
故选:B.
2.B
【详解】解:A. a2 a6 a8,故该选项不正确,不符合题意;
B. 3a 2 9a2,故该选项正确,符合题意;
C. 2a2 3a2 5a2,故该选项不正确,不符合题意;
D. a b 2 a2 2ab b2,故该选项不正确,不符合题意;
故选:B.
3.A
【详解】解:A. 了解一批灯泡的使用寿命,应采用抽样调查的方式,故该选项正确,符合题意;
B. 为了直观地介绍某款牛奶各营养成分的百分比,最适合使用的统计图是扇形统计图,故该选项不正确,
不符合题意;
1
C. 一个抽奖活动中,中奖概率为 ,表示抽奖 20次可能有 1次中奖,故该选项不正确,不符合题意;
20
D. “投掷一枚质地均匀的硬币一次,结果正面朝上”为随机事件,故该选项不正确,不符合题意;
故选:A.
4.D
【详解】解:A、 2 4 2 2 2 4 2 ,不是最简二次根式,故本选项不符合题意;
B、 a2 a ,不是最简二次根式,故本选项不符合题意;
C、 27 3 3 ,不是最简二次根式,故本选项不符合题意;
D、 2是最简二次根式,故本选项符合题意;
故选:D.
5.B
【详解】解:520000000=5.2×108
故选:B.
答案第 1页,共 13页
6.C
【详解】∵∠C=40°,
∴∠AOB=2∠C=80°.
故选 C.
7.C
k
【详解】∵P为反比例数 y= 的图象上一点,PA⊥x轴于点 A,△PAO的面积为 6,
x
k
∴S△PAO= =6,
2
∵反比例函数的图象在二、四象限,
∴k<0,
∴k=-12.
故选 C.
8.D
【详解】试题分析:由 DE与 BC平行,得到△ADE∽△ABC,由相似得比例,根据 AB=AC,得到 AD=AE,
进而确定出 DB=EC,再由两直线平行同位角相等,以及等腰三角形的底角相等,等量代换得到∠ADE=∠C,
而 DE不一定为中位线,即 DE不一定为 BC的一半,即可得到正确选项.
故选 D.
考点:1、等腰三角形的判定与性质;2、平行线的性质
9.C
【详解】解:∵AB是⊙O的直径,
∴∠C=90°,
1
∵sinA= ,BC=1,
4
BC 1
∴ = ,
AB 4
∴AB=4,
∴⊙O的半径等于 2.
故选 C.
10.C
【详解】解:∵抛物线与 x轴的一个交点在点 3,0 和 4,0 之间,而抛物线的对称轴为直线 x 1,
答案第 2页,共 13页
∴抛物线与 x轴的另一个交点在点 2,0 和 1,0 之间.
∴当 x 1时, y 0,
即a b c 0,所以①正确;
∵抛物线与 x轴有两个交点,则b2 4ac 0,所以②正确;
b
∵抛物线的对称轴为直线 x 1,即b 2a,
2a
a b c 0,
a b c a 2a c 3a c 0,所以③正确;
∵抛物线与直线 y n有一个公共点,
∴由图象可得,抛物线与直线 y n 1有两个公共点,
∴一元二次方程 ax2 bx c n 1有两个实数根,所以④错误.
故选:C.
11. x 1
【详解】由题意得:1 x 0, x 1
12.m m 2 .
2
【详解】解:m 2m m m 2 .
故答案为:m m 2 .
13.50
【分析】先根据平行线的性质得出∠3=130°,再由邻补角得到∠2=50°.
【详解】解:如图,
∵ a / /b, 1 130 ,
∴∠3=130°,
又∵∠2+∠3=180°,
∴∠2=180°-∠3=180°-130°=50°.
故答案为:50.
答案第 3页,共 13页
14.m<3
【详解】解:∵x- 2 3 x+m=0有两个不相等的实数根,
∴Δ=(-2 3 )2-4m>0
解得:m<3,
故答案为: m<3.
15.﹣24
【详解】如下图,过点 C作 CF⊥AO于点 F,过点 D作 DE∥OA交 CO于点 E,设 CF=4x,
∵四边形 ABCO是菱形,
∴AB//CO,AO//BC,
∵DE//AO,
∴四边形 AOED和四边形 DECB都是平行四边形,
∴S△AOD=S△DOE,S△BCD=S△CDE,
∴S 菱形ABCD=2S△DOE+2S△CDE=2S△COD=40,
4
∵tan∠AOC= ,CF=4x,
3
∴OF=3x,
∴在 Rt△COF中,由勾股定理可得 OC=5x,
∴OA==OC=5x,
∴S 菱形ABCO=AO·CF=5x·4x=20x2=40,解得:x= 2,
∴OF=3 2,CF= 4 2,
∴点 C的坐标为 ( 3 2,4 2),
k
∵点 C在反比例函数 y 的图象上,
x
∴k= 3 2 4 2 24 .
故答案为:-24.
答案第 4页,共 13页
16.(1)1 3;(2)
1 1
【详解】解:原式=3 3 2 8 1
2 2
=3 3 1﹣2﹣1
=1 3.
16.(2). x1 0, x2 2.
【详解】解: x2 2x 0,
x x 2 0,
x 0或 x 2 0,
∴ x1 0, x2 2.
17. x 1, 5
1 x2 1
【详解】解: 1
x 1 x
x 1 1 (x 1)(x 1)
x 1 x
x x 1
x
x 1
当 x 5 1时,原式 5 1 1 5 .
答案第 5页,共 13页
18.(1)A、B两种型号电脑每台价格分别是 0.5万元和 0.4万元
(2)有 3种方案,即:购买 A种型号电脑 10台、购买 B种型号电脑 10台;购买 A种型号电脑 11台、购买
B种型号电脑 9台;购买 A种型号电脑 12台、购买 B种型号电脑 8台
【详解】(1)解:设 A种型号电脑每台价格为 x万元,则 B种型号电脑每台价格(x﹣0.1)万元.
根据题意得:
10 8
,解得 x 0.5,
x x 0.1
经检验:x=0.5是原方程的解,
x﹣0.1=0.4,
答:A、B两种型号电脑每台价格分别是 0.5万元和 0.4万元.
(2)解:设购买 A种型号电脑 y台,则购买 B种型号电脑(20﹣y)台.
根据题意得:0.5y+0.4(20﹣y)≤9.2,
解得:y≤12,
又∵A种型号电脑至少要购进 10台,
∴10≤y≤12,y的整数解为 10、11、12,
∴有 3种方案.
即:购买 A种型号电脑 10台、购买 B种型号电脑 10台;
购买 A种型号电脑 11台、购买 B种型号电脑 9台;
购买 A种型号电脑 12台、购买 B种型号电脑 8台.
19.(1)100,32;
(2)见解析;
2
(3) 3
54
【详解】(1))15÷ =100,
360
所以样本容量为 100;
B组的人数为 100-15-35-15-5=30,
30
所以 a%= ×100%=30%,则 a=30;
100
故答案为 100,30;
(2)补全频数分布直方图为:
答案第 6页,共 13页
(3)画树状图为:
4 2
共有 6种等可能的结果数,其中“1男 1女”的结果数为 4,所以恰好选中“1男 1女”的概率
6 3
sin CDB 420.(1)详见解析;(2)
5
【详解】(1)证明: CE / /BD,DE / /BC,
四边形 BDEC是平行四边形.
CE BD,
CD是 AB边上的中线,
AD BD,
CE AD,
四边形 ADCE是平行四边形.
ACB 90 ,DE / /BC,
AOD ACB 90 ,
AC DE,
四边形 ADCE是菱形.
(2)解:过点C作CF AB于 F .
答案第 7页,共 13页
平行四边形 BDEC,
DE BC,
AC 2DE,
AC 2BC,
设 BC x,
则 AC 2x,
在 Rt ACB中, ACB 90 ;
AB AC2 BC2 5x.
ACB 90 ,CF AB,
S 1 ABC AC BC
1
AB CF,
2 2
CF 2 5 x,
5
ACB 90;CD是 AB边上的中线,
CD 1 AB 5 x,
2 2
在 Rt CDF中,∠CFD 90 ,
sin CDB CF 4 .
CD 5
21.(1)C坐标为 4,-1
(2) 1 17 1 17( , )
2 2
【详解】(1)解:如图, 过点 B作 BE⊥y轴于点 E,过点 C作 CF⊥y轴于点 F
k
∵反比例函数 y 经过点 B( 1,4),
x
4 k∴ = ,
- 1
解得, k 4
答案第 8页,共 13页
4
∴反比例函数为 y
x
∵BE⊥y轴,CF⊥y轴,
∴BE∥CF,
∴△BEA∽△CFA
∵AC=4AB ,
BE AB 1
∴
CF AC 4
∴CF=4
4
∵反比例函数 y 经过点 C
x
∴当 x 4时, y 1,即点 C坐标为(4, 1)
(2)过点 D作 DG∥y轴,交 AC于点 G.
将点 B( 1,4),点 C(4, 1)代入 y ax b ,解得 a 1,b 3
∴直线的函数解析式为 y x 3
4
设点 D(t, ),点 G(t, t 3)
t
∵ S△BCD =5,
1
∴ 4 -1
-t
4
3 -
52 t
t 1 17 t 1 17解得, 1 , ,2 2 2
∵0 t 4,
t 1 17∴ 1 2
1 17 1 17
此时,点 D的坐标为( , ).
2 2
答案第 9页,共 13页
22.(1)证明见解析
90
(2)
7
【详解】(1)证明:如图所示,连接OC,
∵ AB为 O的直径,
∴ BCA 90 ,
∴∠OBC+∠OCA=90°
∵OC OB,
∴ B OCB,
又∵ ACD B,
∴ ACD OCB,
∴ OCA ACD 90 ,即 OCD 90 ,
∴DC为 O的切线;
(2)解:在Rt△ABC中, AB 10,∠ACB 90 ,sinB
3
,
5
∴ AC AB sin B 6,
∴ BC AB2 AC2 8,
∵∠ACD ∠B,∠D ∠D,
∴△ACD∽△CBD,
答案第 10页,共 13页
AC AD AD 6 3
∴ ,即 ,
BC CD CD 8 4
设 AD 3x,CD 4x ,则OD OA AD 3x 5,
在Rt△OCD中,由勾股定理得:OC2 CD 2 OD2,
52 4x 2 3x 5 2∴ ,
x 30解得 (不合题意的值舍去),
7
∴ AD 3x
90
.
7
23.(1)B(4,0),C(0,﹣2),(2)y= ;(3)E(2,﹣1),EF的最大值为 2;(4)直线
CD是经过 A、B、C三点的圆的切线,理由见解析.
解:(1)由题意知直线 y= x﹣2交 x轴、y轴于点 B、C两点,
∴B(4,0),C(0,﹣2),
(2)∵y=ax2﹣ x+c经过点 B,C,
∴ ,
解得 ,
∴y= ;
(3)如图 1:
答案第 11页,共 13页
设点 E(x, x﹣2),
∵直线 EF∥y轴,
∴点 F(x, ),
EF= x﹣2﹣( ),
EF= = ,
所以当 x=2时,EF有最大值是 2,
此时 E(2,﹣1),EF的最大值为 2;
(4)如图 2:
∵y=ax2﹣ x+c与 x轴相交于 A、B两点,
令 y=0,得 ax2﹣ x+c=0,
解得:x=﹣1,或 x=4,
∴A(﹣1,0),B(4,0),C(0,﹣2),
∴OA=1,OC=2,0B=4,
∴tan∠ACO=tan∠CBO= ,
答案第 12页,共 13页
∴∠ACO=∠CBO,
∵∠OCB+∠CBO=90°,
∴∠ACO+∠OCB=90°,
∴∠ACB=90°,
∴AB是经过 A、B、C三点的圆的直径,
设圆心 Q,则 Q( ,0),连接 QC,过点 D作 DE⊥y轴,垂足为 E,连接 QD,
y= 顶点坐标为 D( , ),
可求 CE=﹣2﹣( )= ,ED= ,CD= ,CQ= = ,QD= ,
计算得:CD2+CQ2=DQ2,
∴∠QCD=90°,
∴直线 CD是经过 A、B、C三点的圆的切线.
答案第 13页,共 13页
同课章节目录
