5.3 第一课时 诱导公式二、三、四-高一年级数学人教版(2019)必修一 课件(共20张PPT)
文档属性
| 名称 | 5.3 第一课时 诱导公式二、三、四-高一年级数学人教版(2019)必修一 课件(共20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-11 16:36:19 | ||
图片预览







文档简介
(共20张PPT)
新教材人教版·高中必修第一册
数学
5.3 诱导公式
5.3第一课时 诱导公式二、三、四
第五章 三角函数
要求
1.了解三角函数的诱导公式的意义与作用.
2.理解诱导公式的推导过程.
3.能运用有关诱导公式解决一些三角函数的求值、化简和证明问题.
借助单位圆的对称性,利用定义推导诱导公式,重点提升学生的逻辑推理、数学运算素养.
复习引入
前面利用圆的几何性质,得到了同角三角函数之间的基本关系,我们知道,圆的最重要的性质是对称性,而对称性(如奇偶性)也是函数的重要性质,由此想到,可以利用圆的对称性,研究三角函数的对称性.
研究诱导公式一时我们已经知道它作用是把求任意角的三角函数值问题转化为求[0,2 π ]间的角的三角函数值问题,诱导公式的推导过程,体现了“数形结合”和复杂到简单的“转化”的数学思想方法,反映了从特殊到一般的归纳思维形式.
复习引入
在学习过程中,我们已习惯与[0 , ]的三角函数求值问题。那么,任意角的三角函数,能否都能转化为[0 , ]上的三角函数呢?
问题1
sin( +k 2 )= sin ,
cos( +k 2 )= cos ,
tan( +k 2 )= tan ,
其中k∈Z.
回顾公式一
它的主要作用将任意角的三角函数,转化为[0 , 2 )上的三角函数。
复习引入
那么如何继续将 [0,2 )间的角的三角函数值转化到我们熟悉的[0 , )间的角的三角函数值呢?
我们发现,有一些角,它们的终边具有某种特殊关系,如关于坐标轴对称、关于原点对称等,那么它们的三角函数值有何关系呢?
如图5.3-1,在直角坐标系内,设任意角 的终边与单位圆交于点P1.
(1)作P1关于原点的对称点P2,以OP2为终边的角序与角 有什么关系?角 , 的三角函数值之间有什么关系?
(2)如果作P1关于x轴(或y轴)的对称点P3(或P4),那么又可以得到什么结论?
公式引入
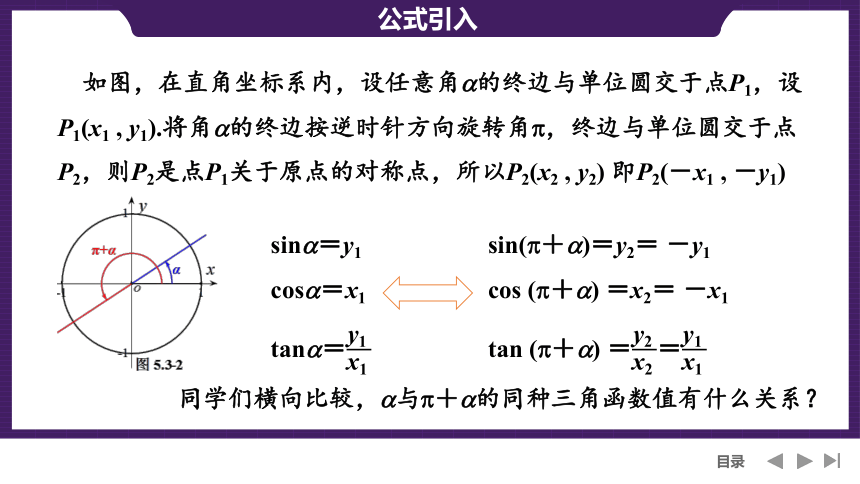
如图,在直角坐标系内,设任意角 的终边与单位圆交于点P1,设P1(x1 , y1).将角 的终边按逆时针方向旋转角 ,终边与单位圆交于点P2,则P2是点P1关于原点的对称点,所以P2(x2 , y2) 即P2(-x1 , -y1)
sin =y1
cos =x1
tan =
sin( + )=y2= -y1
cos ( + ) =x2= -x1
tan ( + ) ==
同学们横向比较, 与 + 的同种三角函数值有什么关系?
公式引入
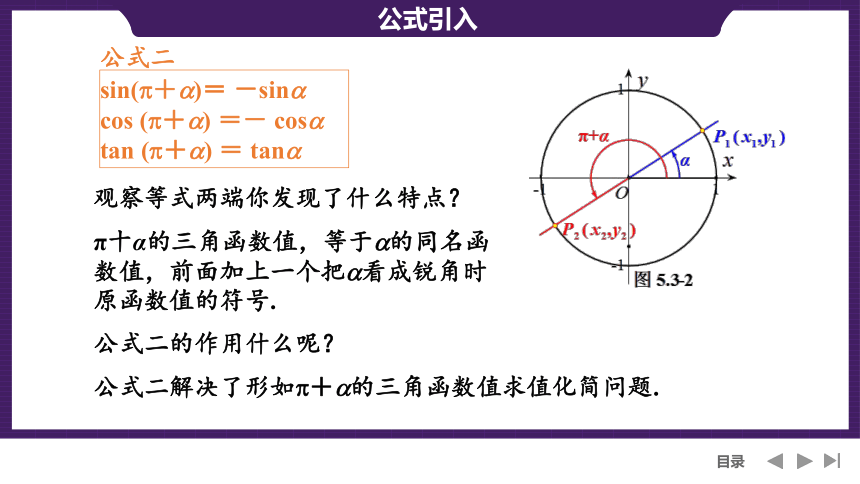
公式二
sin( + )= -sin
cos ( + ) =- cos
tan ( + ) = tan
观察等式两端你发现了什么特点?
π十α的三角函数值,等于 的同名函数值,前面加上一个把 看成锐角时原函数值的符号.
公式二的作用什么呢?
公式二解决了形如 + 的三角函数值求值化简问题.
公式引入
如图5.3-3,作P关于x轴的对称点P3,则以OP3为终边的角为- ,并且有x3=x1 , y3=-y1
公式三
sin(- )= -sin
cos (- ) =cos
tan (- ) = -tan
如图5.3-4,作P关于y轴的对称点P4,则以OP4为终边的角为 - ,并且有x4=-x1 , y4=y1
公式四
sin( - )= sin
cos ( - ) =-cos
tan ( - ) = -tan
公式引入
sin( +k 2 )= sin ,
cos( +k 2 )= cos ,
tan( +k 2 )= tan ,
其中k∈Z.
公式一
公式二
sin( + )= -sin
cos ( + ) =- cos
tan ( + ) = tan
公式三
sin(- )= -sin
cos (- ) =cos
tan (- ) = -tan
公式四
sin( - )= sin
cos ( - ) =-cos
tan ( - ) = -tan
观察每组公式左右两端结构特征,你有什么发现?
公式理解
1、四组公式中, 是任意的,而一般情况下为锐角。
2、左右两端三角函数名称不变, 角不变,只是前面加一个符号;符号的判断方法:把 看成锐角时原函数值的符号,既然 看成锐角,那么进而判断的符号。
即口诀:函数名不变,符号看象限.
巩固与练习
巩固与练习
规律方法
巩固与练习
巩固与练习
规律方法
巩固与练习
深化与思考
√
×
√
×
小结
限时小练
简解答:
课堂作业
教科书P191
2、3、4
本节内容结束
THANKS
新教材人教版·高中必修第一册
数学
5.3 诱导公式
5.3第一课时 诱导公式二、三、四
第五章 三角函数
要求
1.了解三角函数的诱导公式的意义与作用.
2.理解诱导公式的推导过程.
3.能运用有关诱导公式解决一些三角函数的求值、化简和证明问题.
借助单位圆的对称性,利用定义推导诱导公式,重点提升学生的逻辑推理、数学运算素养.
复习引入
前面利用圆的几何性质,得到了同角三角函数之间的基本关系,我们知道,圆的最重要的性质是对称性,而对称性(如奇偶性)也是函数的重要性质,由此想到,可以利用圆的对称性,研究三角函数的对称性.
研究诱导公式一时我们已经知道它作用是把求任意角的三角函数值问题转化为求[0,2 π ]间的角的三角函数值问题,诱导公式的推导过程,体现了“数形结合”和复杂到简单的“转化”的数学思想方法,反映了从特殊到一般的归纳思维形式.
复习引入
在学习过程中,我们已习惯与[0 , ]的三角函数求值问题。那么,任意角的三角函数,能否都能转化为[0 , ]上的三角函数呢?
问题1
sin( +k 2 )= sin ,
cos( +k 2 )= cos ,
tan( +k 2 )= tan ,
其中k∈Z.
回顾公式一
它的主要作用将任意角的三角函数,转化为[0 , 2 )上的三角函数。
复习引入
那么如何继续将 [0,2 )间的角的三角函数值转化到我们熟悉的[0 , )间的角的三角函数值呢?
我们发现,有一些角,它们的终边具有某种特殊关系,如关于坐标轴对称、关于原点对称等,那么它们的三角函数值有何关系呢?
如图5.3-1,在直角坐标系内,设任意角 的终边与单位圆交于点P1.
(1)作P1关于原点的对称点P2,以OP2为终边的角序与角 有什么关系?角 , 的三角函数值之间有什么关系?
(2)如果作P1关于x轴(或y轴)的对称点P3(或P4),那么又可以得到什么结论?
公式引入
如图,在直角坐标系内,设任意角 的终边与单位圆交于点P1,设P1(x1 , y1).将角 的终边按逆时针方向旋转角 ,终边与单位圆交于点P2,则P2是点P1关于原点的对称点,所以P2(x2 , y2) 即P2(-x1 , -y1)
sin =y1
cos =x1
tan =
sin( + )=y2= -y1
cos ( + ) =x2= -x1
tan ( + ) ==
同学们横向比较, 与 + 的同种三角函数值有什么关系?
公式引入
公式二
sin( + )= -sin
cos ( + ) =- cos
tan ( + ) = tan
观察等式两端你发现了什么特点?
π十α的三角函数值,等于 的同名函数值,前面加上一个把 看成锐角时原函数值的符号.
公式二的作用什么呢?
公式二解决了形如 + 的三角函数值求值化简问题.
公式引入
如图5.3-3,作P关于x轴的对称点P3,则以OP3为终边的角为- ,并且有x3=x1 , y3=-y1
公式三
sin(- )= -sin
cos (- ) =cos
tan (- ) = -tan
如图5.3-4,作P关于y轴的对称点P4,则以OP4为终边的角为 - ,并且有x4=-x1 , y4=y1
公式四
sin( - )= sin
cos ( - ) =-cos
tan ( - ) = -tan
公式引入
sin( +k 2 )= sin ,
cos( +k 2 )= cos ,
tan( +k 2 )= tan ,
其中k∈Z.
公式一
公式二
sin( + )= -sin
cos ( + ) =- cos
tan ( + ) = tan
公式三
sin(- )= -sin
cos (- ) =cos
tan (- ) = -tan
公式四
sin( - )= sin
cos ( - ) =-cos
tan ( - ) = -tan
观察每组公式左右两端结构特征,你有什么发现?
公式理解
1、四组公式中, 是任意的,而一般情况下为锐角。
2、左右两端三角函数名称不变, 角不变,只是前面加一个符号;符号的判断方法:把 看成锐角时原函数值的符号,既然 看成锐角,那么进而判断的符号。
即口诀:函数名不变,符号看象限.
巩固与练习
巩固与练习
规律方法
巩固与练习
巩固与练习
规律方法
巩固与练习
深化与思考
√
×
√
×
小结
限时小练
简解答:
课堂作业
教科书P191
2、3、4
本节内容结束
THANKS
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
