5.2.1 第一课时 三角函数的定义-高一年级数学人教版(2019)必修一 课件(共24张PPT)
文档属性
| 名称 | 5.2.1 第一课时 三角函数的定义-高一年级数学人教版(2019)必修一 课件(共24张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 9.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-11 16:36:48 | ||
图片预览







文档简介
(共24张PPT)
新教材人教版·高中必修第一册
数学
5.2 三角函数的概念
5.2.1第一课时 三角函数的定义
第五章 三角函数
要求
1.借助单位圆理解任意角的三角函数定义.
2.能利用定义解决相关问题.
通过对正弦函数、余弦函数、正切函数定义的理解,重点提升学生的数学抽象和直观想象素养.
复习引入
定义中的三个三角函数,对于同样大的一个角来说,如果三角形的大小改变(相似变化),其三角函数值是否改变?
问题1
同学们回忆一下初中三角函数的概念.
提示 不变.
复习引入
在弧度制下,我们已经将角的范围扩展到全体实数.下面借助这些知识研究上一节开头提出的问题.不失一般性,先研究单位圆上点的运动,现在的任务是:如图5.2-1,单位圆⊙O上的点P以A为起点做逆时针方向旋转,建立一个数学模型,刻画点P的位置变化情况.
图5.2-1
概念引入
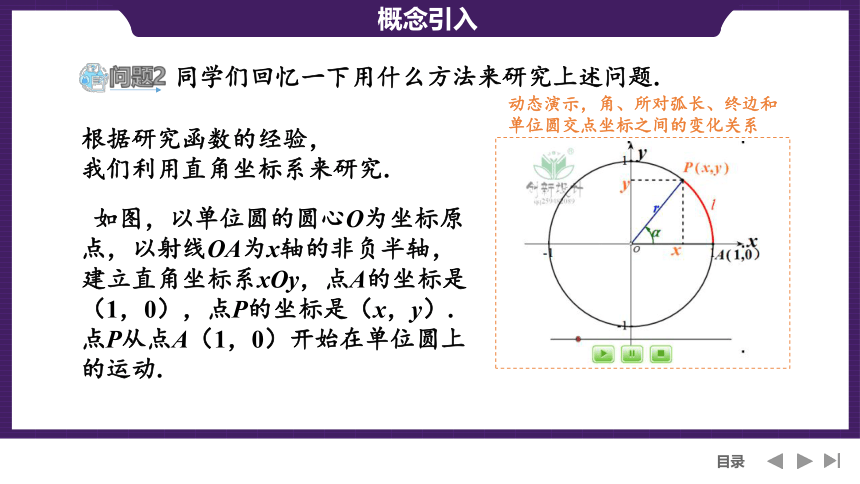
根据研究函数的经验,
我们利用直角坐标系来研究.
问题2
同学们回忆一下用什么方法来研究上述问题.
如图,以单位圆的圆心O为坐标原点,以射线OA为x轴的非负半轴,建立直角坐标系xOy,点A的坐标是(1,0),点P的坐标是(x,y).
点P从点A(1,0)开始在单位圆上的运动.
动态演示,角、所对弧长、终边和单位圆交点坐标之间的变化关系
概念引入
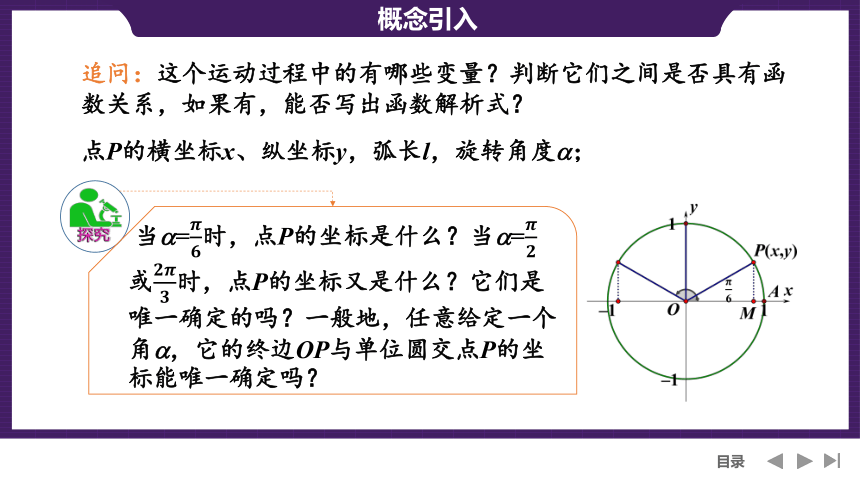
追问:这个运动过程中的有哪些变量?判断它们之间是否具有函数关系,如果有,能否写出函数解析式?
点P的横坐标x、纵坐标y,弧长l,旋转角度 ;
当 =时,点P的坐标是什么?当 =或时,点P的坐标又是什么?它们是唯一确定的吗?一般地,任意给定一个角 ,它的终边OP与单位圆交点P的坐标能唯一确定吗?
概念引入
当 =时,作PM⊥OA与M,
在Rt△OMP中,可得OM=,PM=
x=cos =cos=, x=sin =s=
即P( , );
问题2
同学们思考当 =,时它们的正余弦和P点坐标的关系是?
s=y,cos=,s=y,cos=
同理,当 =或时,P点的坐标分别是
(0 , 1) , (- , ) ,它们都是唯一确定的。
概念引入
一般地,任意给定一个角 ∈R,它的终边OP与单位圆交点P的坐标,无论是横坐标x还是纵坐标y,都是唯一确定的,所以,点P的横坐标x、纵坐标y都是角 的函数.下面给出这些函数的定义.
设 是一个任意角, ∈R ,它的终边OP与单位圆相交于点P(x,y).
(1)把点P的纵坐标y叫做 的正弦函数(sine function),
记作sin ,即y=sin ;
(2)把点P的横坐标x叫做 的余弦函数(cosine function),
记作cos ,即x= cos ;
(3)把点P的纵坐标与横坐标的比值一叫做 的正切,
记作tan ,即=tan (x≠0).
注意:P(x,y)必须是 的终边与单位圆的交点。
概念引入
正弦函数、余弦函数和正切函数统称为三角函数(trigonometric function),通常将它们记为:
正弦函数y=sinx,x∈R;
余弦函数y=cosx,x∈R;
正切函数y=tanx,x≠+k (k∈Z).
温馨提醒 (1)在任意角的三角函数的定义中,α是一个任意角,其范围是使函数有意义的实数集.
(2)由于角的集合与实数集之间可以建立一一对应的关系,所以三角函数可以看成是自变量为实数的函数.
概念理解
问题3
这个定义相对于锐角三角函数的定义有什么不同呢?
任意角的三角函数是通过角与单位圆交点的坐标定义的,锐角三角函数是通过直角三角形边长的比值定义的,在单位圆中直角三角形斜边为1,所以锐角三角函数也可用角的终边与单位圆交点的坐标定义,此时终边上的点都在第一象限,因此锐角三角函数值都是正数,而任意角的三角函数值可以是负数.
概念理解
巩固与练习
巩固与练习
规律方法
单位圆法求三角函数值方法:
首先求出角的终边与单位圆交点的坐标,然后利用任意角的三角函数的定义求解.
优点是交点到原点的距离是1,因此书写运算简洁。
巩固与练习
图5.2-4
图5.2-5
巩固与练习
图5.2-5
图5.2-4
巩固与练习
问题4
请观察右图r与x,y的关系是什么?
图5.2-4
M
r
|x|
|y|
巩固与练习
巩固与练习
巩固与练习
规律方法
深化与思考
小结
限时小练
简解答:
课堂作业
教科书P179练习第2,3题
本节内容结束
THANKS
新教材人教版·高中必修第一册
数学
5.2 三角函数的概念
5.2.1第一课时 三角函数的定义
第五章 三角函数
要求
1.借助单位圆理解任意角的三角函数定义.
2.能利用定义解决相关问题.
通过对正弦函数、余弦函数、正切函数定义的理解,重点提升学生的数学抽象和直观想象素养.
复习引入
定义中的三个三角函数,对于同样大的一个角来说,如果三角形的大小改变(相似变化),其三角函数值是否改变?
问题1
同学们回忆一下初中三角函数的概念.
提示 不变.
复习引入
在弧度制下,我们已经将角的范围扩展到全体实数.下面借助这些知识研究上一节开头提出的问题.不失一般性,先研究单位圆上点的运动,现在的任务是:如图5.2-1,单位圆⊙O上的点P以A为起点做逆时针方向旋转,建立一个数学模型,刻画点P的位置变化情况.
图5.2-1
概念引入
根据研究函数的经验,
我们利用直角坐标系来研究.
问题2
同学们回忆一下用什么方法来研究上述问题.
如图,以单位圆的圆心O为坐标原点,以射线OA为x轴的非负半轴,建立直角坐标系xOy,点A的坐标是(1,0),点P的坐标是(x,y).
点P从点A(1,0)开始在单位圆上的运动.
动态演示,角、所对弧长、终边和单位圆交点坐标之间的变化关系
概念引入
追问:这个运动过程中的有哪些变量?判断它们之间是否具有函数关系,如果有,能否写出函数解析式?
点P的横坐标x、纵坐标y,弧长l,旋转角度 ;
当 =时,点P的坐标是什么?当 =或时,点P的坐标又是什么?它们是唯一确定的吗?一般地,任意给定一个角 ,它的终边OP与单位圆交点P的坐标能唯一确定吗?
概念引入
当 =时,作PM⊥OA与M,
在Rt△OMP中,可得OM=,PM=
x=cos =cos=, x=sin =s=
即P( , );
问题2
同学们思考当 =,时它们的正余弦和P点坐标的关系是?
s=y,cos=,s=y,cos=
同理,当 =或时,P点的坐标分别是
(0 , 1) , (- , ) ,它们都是唯一确定的。
概念引入
一般地,任意给定一个角 ∈R,它的终边OP与单位圆交点P的坐标,无论是横坐标x还是纵坐标y,都是唯一确定的,所以,点P的横坐标x、纵坐标y都是角 的函数.下面给出这些函数的定义.
设 是一个任意角, ∈R ,它的终边OP与单位圆相交于点P(x,y).
(1)把点P的纵坐标y叫做 的正弦函数(sine function),
记作sin ,即y=sin ;
(2)把点P的横坐标x叫做 的余弦函数(cosine function),
记作cos ,即x= cos ;
(3)把点P的纵坐标与横坐标的比值一叫做 的正切,
记作tan ,即=tan (x≠0).
注意:P(x,y)必须是 的终边与单位圆的交点。
概念引入
正弦函数、余弦函数和正切函数统称为三角函数(trigonometric function),通常将它们记为:
正弦函数y=sinx,x∈R;
余弦函数y=cosx,x∈R;
正切函数y=tanx,x≠+k (k∈Z).
温馨提醒 (1)在任意角的三角函数的定义中,α是一个任意角,其范围是使函数有意义的实数集.
(2)由于角的集合与实数集之间可以建立一一对应的关系,所以三角函数可以看成是自变量为实数的函数.
概念理解
问题3
这个定义相对于锐角三角函数的定义有什么不同呢?
任意角的三角函数是通过角与单位圆交点的坐标定义的,锐角三角函数是通过直角三角形边长的比值定义的,在单位圆中直角三角形斜边为1,所以锐角三角函数也可用角的终边与单位圆交点的坐标定义,此时终边上的点都在第一象限,因此锐角三角函数值都是正数,而任意角的三角函数值可以是负数.
概念理解
巩固与练习
巩固与练习
规律方法
单位圆法求三角函数值方法:
首先求出角的终边与单位圆交点的坐标,然后利用任意角的三角函数的定义求解.
优点是交点到原点的距离是1,因此书写运算简洁。
巩固与练习
图5.2-4
图5.2-5
巩固与练习
图5.2-5
图5.2-4
巩固与练习
问题4
请观察右图r与x,y的关系是什么?
图5.2-4
M
r
|x|
|y|
巩固与练习
巩固与练习
巩固与练习
规律方法
深化与思考
小结
限时小练
简解答:
课堂作业
教科书P179练习第2,3题
本节内容结束
THANKS
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
