5.4.2 第二课时 单调性与最值-高一年级数学人教版(2019)必修一 课件(共26张PPT)
文档属性
| 名称 | 5.4.2 第二课时 单调性与最值-高一年级数学人教版(2019)必修一 课件(共26张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-11 16:37:13 | ||
图片预览





文档简介
(共26张PPT)
新教材人教版·高中必修第一册
数学
5.4.2 正弦函数、余弦函数的性质
5.4.2 第二课时 单调性与最值
第五章 三角函数
要求
1.掌握y=sin x,y=cos x的最大值与最小值,并会求简单三角函数的值域和最值.
2.掌握y=sin x,y=cos x的单调性并能利用单调性比较大小.
3.会求函数y=Asin(ωx+φ)及y=Acos(ωx+φ)的单调区间
借助y=sin x与y=cos x的图象,理清单调区间和取得最值的条件,构建直观模型,重点提升学生的直观想象、数学抽象、逻辑推理、数学运算素养.
复习引入
它们的周期都是T=
1、正余弦函数的周期是多少?
2、函数y=Asin( x+ )及函数y=Acos ( x+ )的周期是多少?
(其中A, , 为常数,且A≠0, >0)
它们的周期都是T=2
3、正余弦函数的奇偶性是什么?
y=sinx是奇函数 图像关于原点对称;
y=cosx是偶函数 图像关于y轴对称;
性质引入
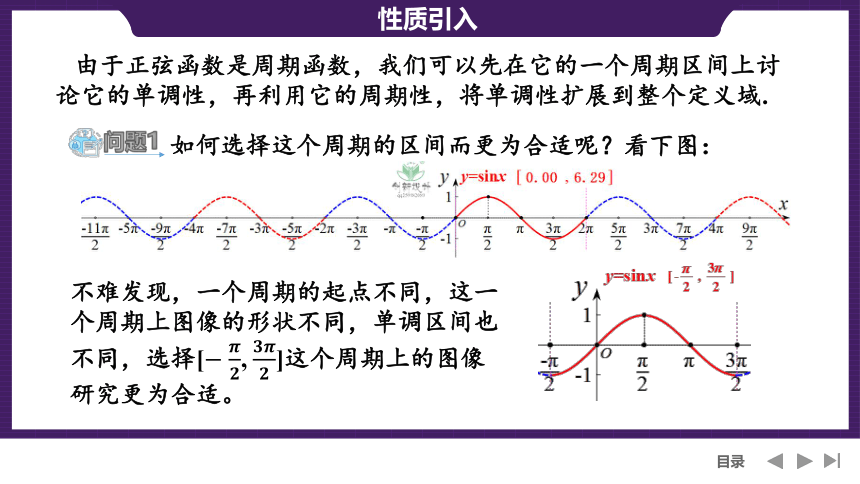
如何选择这个周期的区间而更为合适呢?看下图:
问题1
由于正弦函数是周期函数,我们可以先在它的一个周期区间上讨论它的单调性,再利用它的周期性,将单调性扩展到整个定义域.
不难发现,一个周期的起点不同,这一个周期上图像的形状不同,单调区间也不同,选择[, ]这个周期上的图像研究更为合适。
性质引入
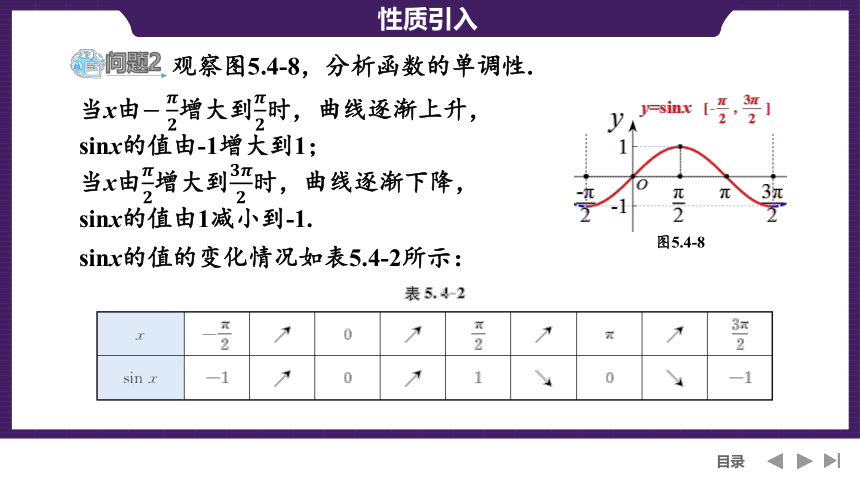
观察图5.4-8,分析函数的单调性.
问题2
当x由增大到时,曲线逐渐上升,sinx的值由-1增大到1;
当x由增大到时,曲线逐渐下降,
sinx的值由1减小到-1.
图5.4-8
sinx的值的变化情况如表5.4-2所示:
性质探究
这就是说,正弦函数y=sinx在区间[, ],上单调递增,
在区间[, ] ,上单调递减。由正弦函数的周期性可得,
正弦函数在
每一个闭区间[+2k , +2k ](k∈Z) 上都单调递增,
其值从-1增大到1;
每一个闭区间[+2k , +2k ](k∈Z) 上都单调递减,
其值从1减小到-1 ;
1、正弦函数的单调性
性质探究
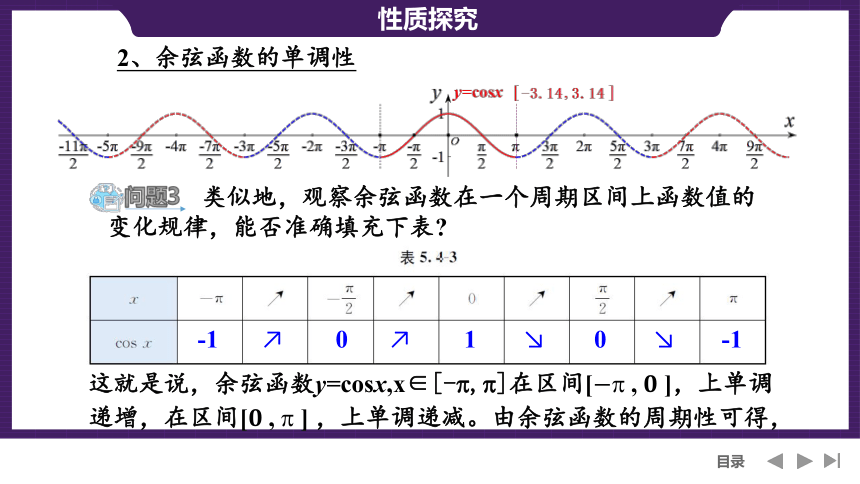
类似地,观察余弦函数在一个周期区间上函数值的变化规律,能否准确填充下表
问题3
-1
-1
1
0
0
↗
↗
↘
↘
这就是说,余弦函数y=cosx,x∈[- , ]在区间[, ],上单调递增,在区间[, ] ,上单调递减。由余弦函数的周期性可得,
2、余弦函数的单调性
性质探究
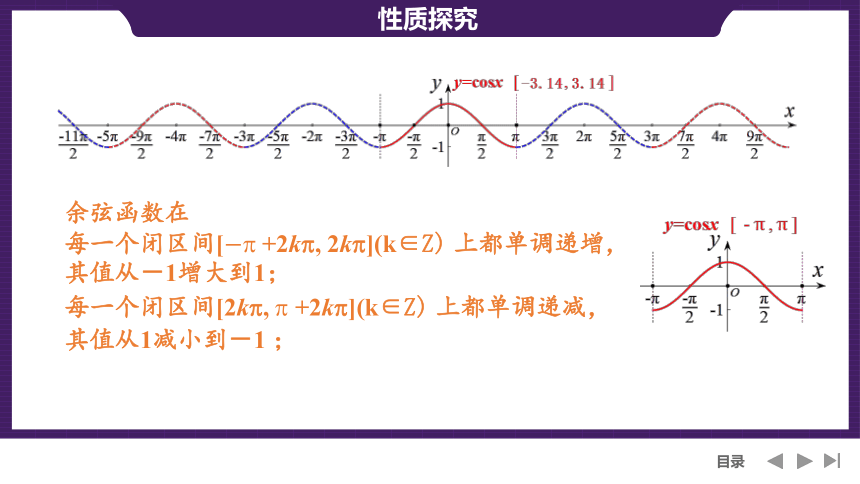
余弦函数在
每一个闭区间[+2k , 2k ](k∈Z) 上都单调递增,
其值从-1增大到1;
每一个闭区间[2k , +2k ](k∈Z) 上都单调递减,
其值从1减小到-1 ;
性质探究
正弦函数当且仅当_______________时取得最大值1,
当且仅当________________时取得最小值-1;
由正余弦函数的单调性的讨论,你能总结它们何时取得最大值,何时取得最小值?
问题4
余弦函数当且仅当____________时取得最大值1,
当且仅当 _______________时取得最小值-1;
x=+2k ,k∈Z
x=+2k ,k∈Z
x=2k ,k∈Z
x=2(k+1) ,k∈Z
3、三角函数的最值
巩固与练习
(1)使函数y=cosx+1,x∈R取得最大值的x的集合,就是使函数y=cosx, x∈R取得最大值的x的集合
函数y=cosx+1, x∈R的最大值是1+1=2;最小值是-1+1=0.
{x | x =2k ,k ∈Z};
使函数y=cosx+1,x∈R取得最小值的x的集合,就是使函数y=cosx, x∈R取得最小值的x的集合
{x | x =(2k+1) ,k ∈Z};
巩固与练习
(2)令z=2x,使函数y=-3sinz,z∈R取得最大值的z的集合,就是使y=sinz,z∈R取得最小值的z的集合
{x | x =-+2k ,k ∈Z};
由2x=z -+2k , 得x =-+k .
所以,使函数y=-3sin 2x,x∈R取得最大值的x的集合是
{x | x =+k ,k ∈Z}.
巩固与练习
函数y=-3sin 2x,x∈R的最大值是3,最小值是-3.
同理,使函数y=-3sin 2x, x∈R取得最小值的x的集合是
{x | x =+k ,k ∈Z}.
巩固与练习
此类函数,求单调区间,当自变量的系数为负时,尽量根据诱导公式将系数变为正。
巩固与练习
巩固与练习
规律方法
巩固与练习
分析:可利用三角函数的单调性比较两个同名三角函数值的大小,为此,先用诱导公式将已知角化为同一单调区间内的角,然后再比较大小.
巩固与练习
巩固与练习
规律方法
巩固与练习
巩固与练习
深化与思考
×
×
×
√
小结
小结
限时小练
简解答:
课堂作业
1、教科书P207 第2、4、5题
2、认真阅读208页“探索与发现”
本节内容结束
THANKS
新教材人教版·高中必修第一册
数学
5.4.2 正弦函数、余弦函数的性质
5.4.2 第二课时 单调性与最值
第五章 三角函数
要求
1.掌握y=sin x,y=cos x的最大值与最小值,并会求简单三角函数的值域和最值.
2.掌握y=sin x,y=cos x的单调性并能利用单调性比较大小.
3.会求函数y=Asin(ωx+φ)及y=Acos(ωx+φ)的单调区间
借助y=sin x与y=cos x的图象,理清单调区间和取得最值的条件,构建直观模型,重点提升学生的直观想象、数学抽象、逻辑推理、数学运算素养.
复习引入
它们的周期都是T=
1、正余弦函数的周期是多少?
2、函数y=Asin( x+ )及函数y=Acos ( x+ )的周期是多少?
(其中A, , 为常数,且A≠0, >0)
它们的周期都是T=2
3、正余弦函数的奇偶性是什么?
y=sinx是奇函数 图像关于原点对称;
y=cosx是偶函数 图像关于y轴对称;
性质引入
如何选择这个周期的区间而更为合适呢?看下图:
问题1
由于正弦函数是周期函数,我们可以先在它的一个周期区间上讨论它的单调性,再利用它的周期性,将单调性扩展到整个定义域.
不难发现,一个周期的起点不同,这一个周期上图像的形状不同,单调区间也不同,选择[, ]这个周期上的图像研究更为合适。
性质引入
观察图5.4-8,分析函数的单调性.
问题2
当x由增大到时,曲线逐渐上升,sinx的值由-1增大到1;
当x由增大到时,曲线逐渐下降,
sinx的值由1减小到-1.
图5.4-8
sinx的值的变化情况如表5.4-2所示:
性质探究
这就是说,正弦函数y=sinx在区间[, ],上单调递增,
在区间[, ] ,上单调递减。由正弦函数的周期性可得,
正弦函数在
每一个闭区间[+2k , +2k ](k∈Z) 上都单调递增,
其值从-1增大到1;
每一个闭区间[+2k , +2k ](k∈Z) 上都单调递减,
其值从1减小到-1 ;
1、正弦函数的单调性
性质探究
类似地,观察余弦函数在一个周期区间上函数值的变化规律,能否准确填充下表
问题3
-1
-1
1
0
0
↗
↗
↘
↘
这就是说,余弦函数y=cosx,x∈[- , ]在区间[, ],上单调递增,在区间[, ] ,上单调递减。由余弦函数的周期性可得,
2、余弦函数的单调性
性质探究
余弦函数在
每一个闭区间[+2k , 2k ](k∈Z) 上都单调递增,
其值从-1增大到1;
每一个闭区间[2k , +2k ](k∈Z) 上都单调递减,
其值从1减小到-1 ;
性质探究
正弦函数当且仅当_______________时取得最大值1,
当且仅当________________时取得最小值-1;
由正余弦函数的单调性的讨论,你能总结它们何时取得最大值,何时取得最小值?
问题4
余弦函数当且仅当____________时取得最大值1,
当且仅当 _______________时取得最小值-1;
x=+2k ,k∈Z
x=+2k ,k∈Z
x=2k ,k∈Z
x=2(k+1) ,k∈Z
3、三角函数的最值
巩固与练习
(1)使函数y=cosx+1,x∈R取得最大值的x的集合,就是使函数y=cosx, x∈R取得最大值的x的集合
函数y=cosx+1, x∈R的最大值是1+1=2;最小值是-1+1=0.
{x | x =2k ,k ∈Z};
使函数y=cosx+1,x∈R取得最小值的x的集合,就是使函数y=cosx, x∈R取得最小值的x的集合
{x | x =(2k+1) ,k ∈Z};
巩固与练习
(2)令z=2x,使函数y=-3sinz,z∈R取得最大值的z的集合,就是使y=sinz,z∈R取得最小值的z的集合
{x | x =-+2k ,k ∈Z};
由2x=z -+2k , 得x =-+k .
所以,使函数y=-3sin 2x,x∈R取得最大值的x的集合是
{x | x =+k ,k ∈Z}.
巩固与练习
函数y=-3sin 2x,x∈R的最大值是3,最小值是-3.
同理,使函数y=-3sin 2x, x∈R取得最小值的x的集合是
{x | x =+k ,k ∈Z}.
巩固与练习
此类函数,求单调区间,当自变量的系数为负时,尽量根据诱导公式将系数变为正。
巩固与练习
巩固与练习
规律方法
巩固与练习
分析:可利用三角函数的单调性比较两个同名三角函数值的大小,为此,先用诱导公式将已知角化为同一单调区间内的角,然后再比较大小.
巩固与练习
巩固与练习
规律方法
巩固与练习
巩固与练习
深化与思考
×
×
×
√
小结
小结
限时小练
简解答:
课堂作业
1、教科书P207 第2、4、5题
2、认真阅读208页“探索与发现”
本节内容结束
THANKS
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
