人教版七年级下册 第六章实数单元练习(含答案)
文档属性
| 名称 | 人教版七年级下册 第六章实数单元练习(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 199.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-12 16:57:39 | ||
图片预览


文档简介
第六章 实数 单元练习
一、单选题
1.在3.14,,,,π这五个数中,无理数的个数是( )
A.1 B.2 C.3 D.4
2.满足的整数x是( )
A.,,1,2,3 B.,0,1,2
C.,,0,1,2 D.,0,1,2,3
3.9的算术平方根是( ).
A.3 B. C. D.
4.下列说法正确的有( )个.
①任何实数都可以开立方;
②0的相反数、倒数、平方都是0;
③数轴上的点和有理数——对应;
④有限小数和无限循环小数都是有理数;
⑤无理数都是无限小数
A.1 B.2 C.3 D.4
5.一个正数的两个平方根分别是2m-1和4-3m,则这个正数是( )
A.25 B.15 C.4 D.8
6.若n是正整数,是整数.则n的最小值( )
A.1 B.2 C.3 D.12
7.的立方根是( )
A.
B.
C.
D.
8.-2的值在( )
A.1和2之间 B.2和3之间
C.3和4之间 D.4和5之间
9.下列各式正确的是
A. B. C. D.
10.若x,y都表示有理数,那么下列各式一定为正数的是( )
A. B. C. D.
11.下列说法错误的是( )
A.1的平方根是±1 B.-1的立方根是
C.是的平方根 D.是2的平方根
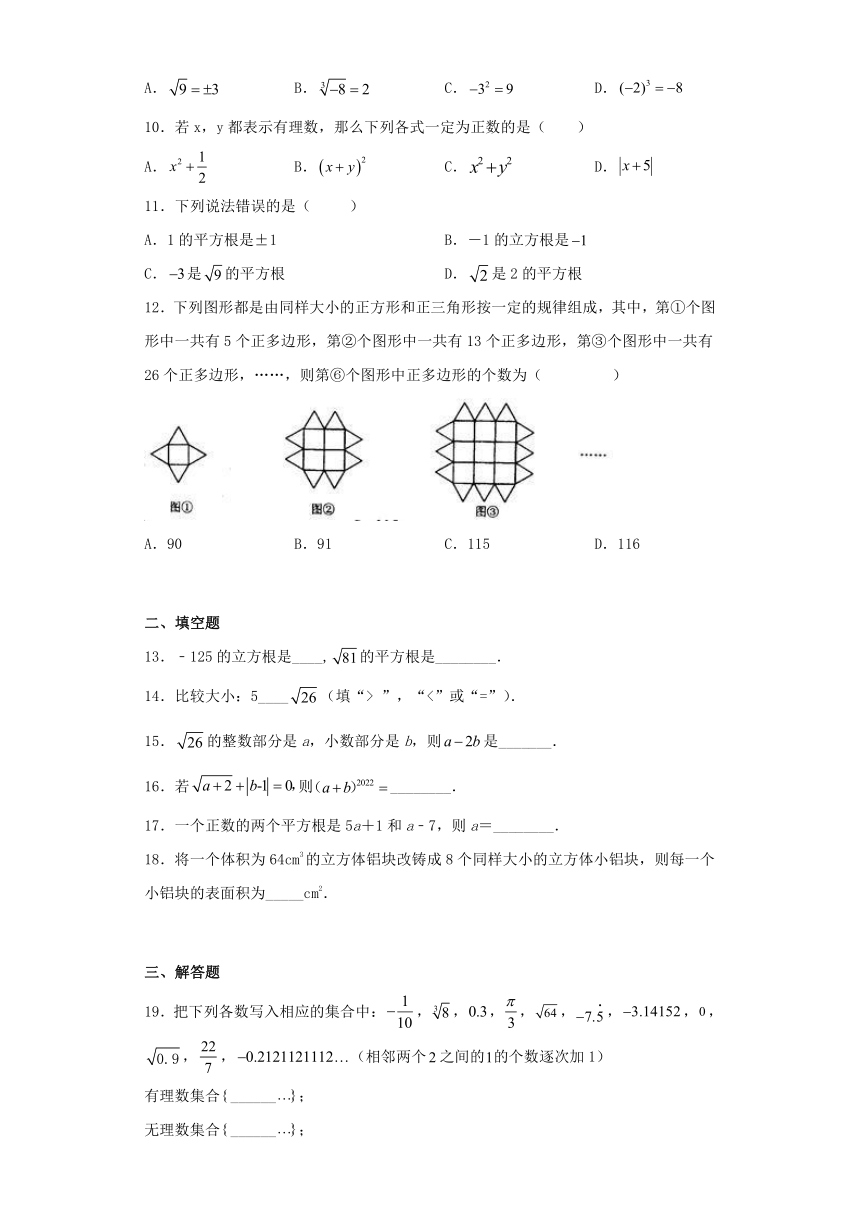
12.下列图形都是由同样大小的正方形和正三角形按一定的规律组成,其中,第①个图形中一共有5个正多边形,第②个图形中一共有13个正多边形,第③个图形中一共有26个正多边形,……,则第⑥个图形中正多边形的个数为( )
A.90 B.91 C.115 D.116
二、填空题
13.﹣125的立方根是____,的平方根是________.
14.比较大小:5____(填“> ”,“<”或“=”).
15.的整数部分是a,小数部分是b,则是_______.
16.若则________.
17.一个正数的两个平方根是5a+1和a﹣7,则a=________.
18.将一个体积为64cm3的立方体铝块改铸成8个同样大小的立方体小铝块,则每一个小铝块的表面积为_____cm2.
三、解答题
19.把下列各数写入相应的集合中:,,,,,,,,,,(相邻两个之间的的个数逐次加1)
有理数集合______;
无理数集合______;
正实数集合______;
负实数集合______.
20.计算:
(1)
(2)
21.计算: + ()-2 - 8sin60°
22.已知3m-2的算术平方根是2,2n-m-8的立方根是﹣2,求m2﹣n2的平方根.
23.求下列各式中的值:
(1);
(2).
24.先观察下列等式,再回答下列问题:
①;
②;
③.
(1)请你根据上面三个等式提供的信息,猜想的结果,并验证;
(2)请你按照上面各等式反映的规律,试写出用含n的式子表示的等式(n为正整数).
参考答案
1.B
2.B
3.A
4.C
5.A
6.C
7.A
8.B
9.D
10.A
11.C
12.C
13. -5, -3、3.
14.
15.-2+15
16.1
17.1
18.24
19解:有理数集合:,,,,,,,;
无理数集合:,,(相邻两个之间的的个数逐次加1);
正实数集合:,,,,,
负实数集合:,,,(相邻两个之间的的个数逐次加1).
故答案为:,,,,,,,;,,(相邻两个之间的的个数逐次加1);,,,,,;,,,(相邻两个之间的的个数逐次加1).
20.解:(1)
=
=;
(2),
∴,
∴,
解得:,.
21.原式=2+4- 8×= 2+4 - 4=4 - 2
22.由题意得:3m-2=4,2n-m-8=-8,解得m=2,n=1,
则m2﹣n2=4-1=3,则m2﹣n2的平方根为 .
23.(1)
直接开平方得:,
解得:,
(2)
两边同时除以3得:,
开立方得:.
24.解:
(1),
验证:=;
(2)(n为正整数).
一、单选题
1.在3.14,,,,π这五个数中,无理数的个数是( )
A.1 B.2 C.3 D.4
2.满足的整数x是( )
A.,,1,2,3 B.,0,1,2
C.,,0,1,2 D.,0,1,2,3
3.9的算术平方根是( ).
A.3 B. C. D.
4.下列说法正确的有( )个.
①任何实数都可以开立方;
②0的相反数、倒数、平方都是0;
③数轴上的点和有理数——对应;
④有限小数和无限循环小数都是有理数;
⑤无理数都是无限小数
A.1 B.2 C.3 D.4
5.一个正数的两个平方根分别是2m-1和4-3m,则这个正数是( )
A.25 B.15 C.4 D.8
6.若n是正整数,是整数.则n的最小值( )
A.1 B.2 C.3 D.12
7.的立方根是( )
A.
B.
C.
D.
8.-2的值在( )
A.1和2之间 B.2和3之间
C.3和4之间 D.4和5之间
9.下列各式正确的是
A. B. C. D.
10.若x,y都表示有理数,那么下列各式一定为正数的是( )
A. B. C. D.
11.下列说法错误的是( )
A.1的平方根是±1 B.-1的立方根是
C.是的平方根 D.是2的平方根
12.下列图形都是由同样大小的正方形和正三角形按一定的规律组成,其中,第①个图形中一共有5个正多边形,第②个图形中一共有13个正多边形,第③个图形中一共有26个正多边形,……,则第⑥个图形中正多边形的个数为( )
A.90 B.91 C.115 D.116
二、填空题
13.﹣125的立方根是____,的平方根是________.
14.比较大小:5____(填“> ”,“<”或“=”).
15.的整数部分是a,小数部分是b,则是_______.
16.若则________.
17.一个正数的两个平方根是5a+1和a﹣7,则a=________.
18.将一个体积为64cm3的立方体铝块改铸成8个同样大小的立方体小铝块,则每一个小铝块的表面积为_____cm2.
三、解答题
19.把下列各数写入相应的集合中:,,,,,,,,,,(相邻两个之间的的个数逐次加1)
有理数集合______;
无理数集合______;
正实数集合______;
负实数集合______.
20.计算:
(1)
(2)
21.计算: + ()-2 - 8sin60°
22.已知3m-2的算术平方根是2,2n-m-8的立方根是﹣2,求m2﹣n2的平方根.
23.求下列各式中的值:
(1);
(2).
24.先观察下列等式,再回答下列问题:
①;
②;
③.
(1)请你根据上面三个等式提供的信息,猜想的结果,并验证;
(2)请你按照上面各等式反映的规律,试写出用含n的式子表示的等式(n为正整数).
参考答案
1.B
2.B
3.A
4.C
5.A
6.C
7.A
8.B
9.D
10.A
11.C
12.C
13. -5, -3、3.
14.
15.-2+15
16.1
17.1
18.24
19解:有理数集合:,,,,,,,;
无理数集合:,,(相邻两个之间的的个数逐次加1);
正实数集合:,,,,,
负实数集合:,,,(相邻两个之间的的个数逐次加1).
故答案为:,,,,,,,;,,(相邻两个之间的的个数逐次加1);,,,,,;,,,(相邻两个之间的的个数逐次加1).
20.解:(1)
=
=;
(2),
∴,
∴,
解得:,.
21.原式=2+4- 8×= 2+4 - 4=4 - 2
22.由题意得:3m-2=4,2n-m-8=-8,解得m=2,n=1,
则m2﹣n2=4-1=3,则m2﹣n2的平方根为 .
23.(1)
直接开平方得:,
解得:,
(2)
两边同时除以3得:,
开立方得:.
24.解:
(1),
验证:=;
(2)(n为正整数).
