9.1.1 不等式及其解集(1)
文档属性
| 名称 | 9.1.1 不等式及其解集(1) |  | |
| 格式 | zip | ||
| 文件大小 | 133.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-05-23 16:29:48 | ||
图片预览





文档简介
课件13张PPT。不等式及其解集(1)想一想一辆匀速行驶的汽车在11:20距离A地50千米,
在12:00之前驶过A地,车速应满足什么条件?若设车速为X千米/小时,你能用一个式子表示吗?1、不等式的定义.2、不等式的解与不等式的解集的区别与 联系.3、不等式解集在数轴上的表示.一、确定目标,合作探究二、师生互动 理解新知
不等式:像这样,用“<”和“>”号表示大小关系 的式子,叫做不等式。
像a+2 ≠a-2这样用“≠”表示不等关系的式子也是不等式。
通常我们把用符号“≥”“≤”表示大小关系的式子也称为不等式。【不等式的解 】使不等式成立的未知数的值。【不等式的解集】 使不等式成立的未知数的取值范围叫做不等式的解的集合,简称解集。【解不等式】求不等式的解集的过程。(1)解集中包括了每一个解。
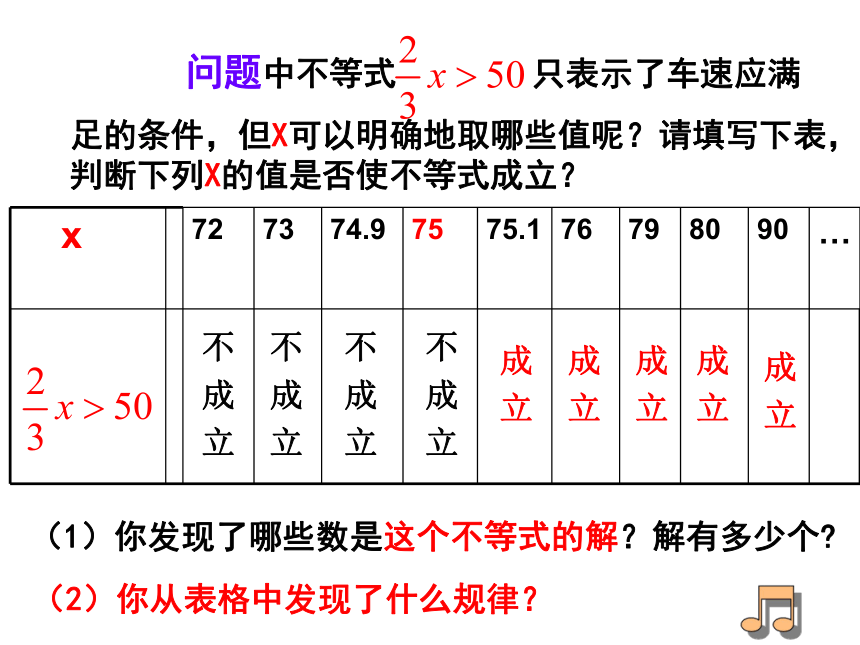
(2)解集是一个范围。 问题中不等式 只表示了车速应满
足的条件,但X可以明确地取哪些值呢?请填写下表,判断下列X的值是否使不等式成立?(2)你从表格中发现了什么规律?(1)你发现了哪些数是这个不等式的解?解有多少个?不
成
立不
成
立不
成
立不
成
立成
立成
立成
立成
立成
立空心圆圈“。”表示“>”或“<”
实心圆点“·”表示“≥”或“≤”即:若解集中含有等号的以实点圆点表示,若解集中不含等号的以空心圆圈表示。75 0X>75画一画: 利用数轴来表示下列不等式的解集.
(1)x>-1 (2)x< (3) x<3; (4)x≥2;
(5)1≤x≤4变 式: 已知x的取值范围如图所示,你能写出x的取值范围吗?空心圆圈“°”表示“>”或“<”
实心圆点“·”表示“≥”或“≤”即:若解集中含有等号则以实点圆点表示,若解集中不含等号的空心圆圈表示。(1)不等式x-1>0有无数个解。(3)x=1是不等式x+2<3的解(4) x=-2是不等式x+2<3的解集。(2)不等式2x <8的解集为x <4三、反馈检测(5)所有小于1的整数都是不等式X <1的解(对)(对)(错)(错)(对)1、2.下列数值哪些是不等式x+3>6的解?哪些不是?
-4, -2.5, 0, 1, 2.5, 3, 3.2, 4.8, 8, 12,3、用不等式表示:
(1)a是负数; (2)a是非负数;
(3)a与b的和小于5; (4)x与2的差大于-1;
(5)x的4倍不大于7; (6)y的一半不小于3.a<0a≥0a+b<5X-2>-14x ≤7≥34.将下列不等式的解集表示在数轴上:
(1)x > 4 ; (2)x < -1 ;
(3)x≥-2 ; (4) x ≤ 6。
5.在数轴上观察
(1) x ≥-2的负整数解有哪些?
(2) x ≤6的非负整数解有哪些?(2)写出适合不等式-1≤x≤5的所有整数,即不等式-1≤x≤5的整数解,其中哪些整数同时适合不等式-1<x<5?(1)找出不等式3x-1>5的五个解,并比较它们与方程3x-1=5的解的大小。四 拓展延伸通过本节的学习,你学到了什么?有什么收获?还有哪些不明白要老师帮助的?1、不等式,以及一元一次不等式的定义.2、不等式的解与不等式的解集的区别与联系.3、不等式解集在数轴上的表示.作业:128页 1,2,3五 知识小结
在12:00之前驶过A地,车速应满足什么条件?若设车速为X千米/小时,你能用一个式子表示吗?1、不等式的定义.2、不等式的解与不等式的解集的区别与 联系.3、不等式解集在数轴上的表示.一、确定目标,合作探究二、师生互动 理解新知
不等式:像这样,用“<”和“>”号表示大小关系 的式子,叫做不等式。
像a+2 ≠a-2这样用“≠”表示不等关系的式子也是不等式。
通常我们把用符号“≥”“≤”表示大小关系的式子也称为不等式。【不等式的解 】使不等式成立的未知数的值。【不等式的解集】 使不等式成立的未知数的取值范围叫做不等式的解的集合,简称解集。【解不等式】求不等式的解集的过程。(1)解集中包括了每一个解。
(2)解集是一个范围。 问题中不等式 只表示了车速应满
足的条件,但X可以明确地取哪些值呢?请填写下表,判断下列X的值是否使不等式成立?(2)你从表格中发现了什么规律?(1)你发现了哪些数是这个不等式的解?解有多少个?不
成
立不
成
立不
成
立不
成
立成
立成
立成
立成
立成
立空心圆圈“。”表示“>”或“<”
实心圆点“·”表示“≥”或“≤”即:若解集中含有等号的以实点圆点表示,若解集中不含等号的以空心圆圈表示。75 0X>75画一画: 利用数轴来表示下列不等式的解集.
(1)x>-1 (2)x< (3) x<3; (4)x≥2;
(5)1≤x≤4变 式: 已知x的取值范围如图所示,你能写出x的取值范围吗?空心圆圈“°”表示“>”或“<”
实心圆点“·”表示“≥”或“≤”即:若解集中含有等号则以实点圆点表示,若解集中不含等号的空心圆圈表示。(1)不等式x-1>0有无数个解。(3)x=1是不等式x+2<3的解(4) x=-2是不等式x+2<3的解集。(2)不等式2x <8的解集为x <4三、反馈检测(5)所有小于1的整数都是不等式X <1的解(对)(对)(错)(错)(对)1、2.下列数值哪些是不等式x+3>6的解?哪些不是?
-4, -2.5, 0, 1, 2.5, 3, 3.2, 4.8, 8, 12,3、用不等式表示:
(1)a是负数; (2)a是非负数;
(3)a与b的和小于5; (4)x与2的差大于-1;
(5)x的4倍不大于7; (6)y的一半不小于3.a<0a≥0a+b<5X-2>-14x ≤7≥34.将下列不等式的解集表示在数轴上:
(1)x > 4 ; (2)x < -1 ;
(3)x≥-2 ; (4) x ≤ 6。
5.在数轴上观察
(1) x ≥-2的负整数解有哪些?
(2) x ≤6的非负整数解有哪些?(2)写出适合不等式-1≤x≤5的所有整数,即不等式-1≤x≤5的整数解,其中哪些整数同时适合不等式-1<x<5?(1)找出不等式3x-1>5的五个解,并比较它们与方程3x-1=5的解的大小。四 拓展延伸通过本节的学习,你学到了什么?有什么收获?还有哪些不明白要老师帮助的?1、不等式,以及一元一次不等式的定义.2、不等式的解与不等式的解集的区别与联系.3、不等式解集在数轴上的表示.作业:128页 1,2,3五 知识小结
