人教版(2019)选择性必修一 1.4 弹性碰撞与非弹性碰撞 课件16张
文档属性
| 名称 | 人教版(2019)选择性必修一 1.4 弹性碰撞与非弹性碰撞 课件16张 | 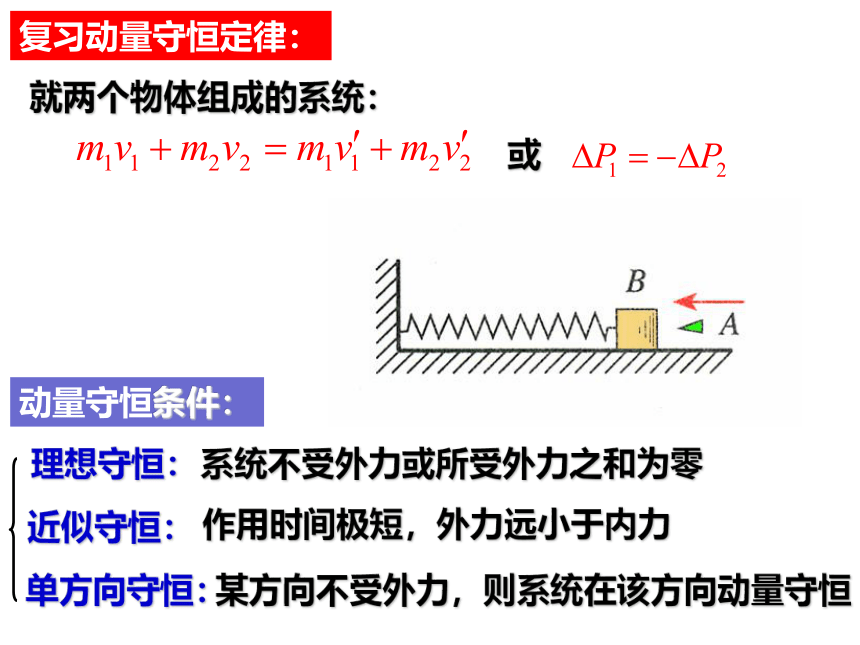 | |
| 格式 | ppt | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-04-11 22:07:07 | ||
图片预览






文档简介
(共16张PPT)
复习动量守恒定律:
就两个物体组成的系统:
或
系统不受外力或所受外力之和为零
作用时间极短,外力远小于内力
某方向不受外力,则系统在该方向动量守恒
理想守恒:
近似守恒:
单方向守恒:
动量守恒条件:
1.5 动量守恒定律应用(2)
---- 弹性碰撞和非弹性碰撞
物理选修1第一章:
一、生活中的碰撞:
最早发表有关碰撞问题研究成果的是布拉格大学校长、物理学教授马尔西(1595—1667),他在1639年发表的《运动的比例》中得出一些碰撞的结论。随后著名的物理学家如伽利略、马略特、牛顿、笛卡尔、惠更斯等都先后进行了一系列的实验总结出碰撞规律,为动量守恒定律的建立奠定了基础。
碰撞:
相对运动的物体相遇在极短时间内通过相互作用,
运动状态发生了明显变化的过程
范围:
宏观物体间的碰撞:
如星体撞击、列车相撞、球相撞
微观物体间的碰撞:
如电子碰撞、粒子轰击原子核等
即使是很小的物体,当运动速度变化很快时,瞬时力可以达到惊人的程度。有关资料介绍,一只重17.8N的飞鸟与运动着的飞机相撞,如果飞机速度是800km/h,碰撞力可高达3.56 105N,即为鸟重的2 104 倍!
一、生活中的碰撞:
不利因素:由于碰撞会损坏机械、仪器等物品。
有利方面:利用碰撞进行工作,如锻打金属,打桩等。
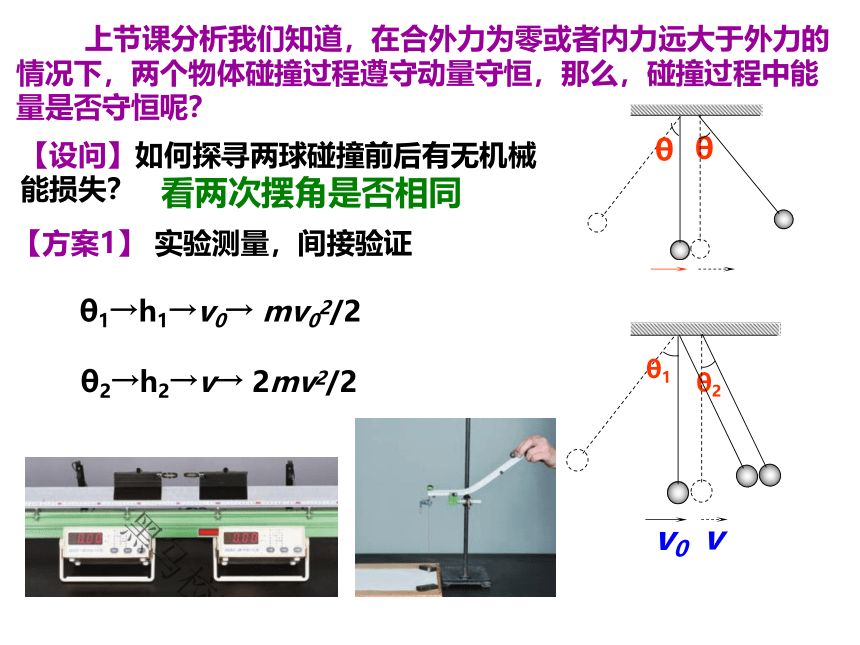
【方案1】 实验测量,间接验证
θ2
θ1
v
v0
θ1→h1→v0→ mv02/2
θ2→h2→v→ 2mv2/2
θ
θ
【设问】如何探寻两球碰撞前后有无机械能损失?
看两次摆角是否相同
上节课分析我们知道,在合外力为零或者内力远大于外力的情况下,两个物体碰撞过程遵守动量守恒,那么,碰撞过程中能量是否守恒呢?
由动量守恒定律:
碰撞前系统总动能:
碰撞后系统总动能:
碰撞过程中有机械能损失
【方案2】 :理论论证:
v
v0
m
2m
m
v1
v共
弹性碰撞
非弹性碰撞
完全非
弹性碰撞
二、碰撞的分类:
分类方式一:从能量变化角度分
碰撞过程中机械能守恒
碰撞过程中机械能不守恒
碰撞后粘在一起,以共同速度运动
1、弹性碰撞:
2、非弹性碰撞:
3、完全非弹性碰撞:
机械能损失最大!
碰撞过程中能量与形变量的演变:
【★讨论问题】
一维弹性碰撞的碰后速度的确定?
v1
v1/
m1
v2/
m2
m1
m2
(对心碰撞、正碰)
质量相等的两物体弹性碰撞后 交换速度
若A、B两物分别以v1、v2运动 则
质量相等的两物体弹性
碰撞后交换速度仍成立
θ
θ
例1、在光滑水平面上,动能为E0、动量的大小为P0的小钢球1与静止的小钢球2发生碰撞,碰撞前后球1的运动方向相反,将碰撞后球1的动能和动量的大小分别记为E1、P1,球2的动能和动量的大小分别记为E2、P2,则必有:
A、E1C、E2>E0 D、P2>P0
1、动量制约
2、动能制约
3、运动制约
——不增
——合理
碰撞规律总结
—— 守恒
二、碰撞的分类:
分类方式二:从碰撞速度方向分
1、对心碰撞——正碰:
2、非对心碰撞——斜碰:
碰前运动速度与两球心连线处于同一直线上,碰后,两球仍沿这条直线
碰前运动速度与两球心连线不在同一直线上,碰后,两球速度都会偏离原来两球的连线
3、散射:
中子的发现:1932年查德威克(英国)
中子减速剂:石墨、重水
微观世界碰撞现象简单介绍:
碰撞特点
相互作用时间极短;
平均作用力(内力)很大
系统所受外力之和通常远小于内力,可忽略。
宏观物体碰撞前后的位置可认为不变
系统总动能不可能增加,即:E K前≥E K后
因此,系统动量近似守恒
碰撞分类
弹性碰撞 →动量、机械能守恒
非弹性碰撞 →动量守恒、机械能有损失
完全非弹性碰撞 →动量守恒、机械能损失最大
对心碰撞(正碰)→碰撞前后速度沿球心连线
非对心碰撞(斜碰)→碰撞前后速度不共线
小结:
例3、质量为m速度为v的A球,跟质量为3m的静止B球发生正碰,碰撞可能是弹性,也可能非弹性,碰后B球的速度可能是以下值吗?
(A)0.6v (B)0.4v (C)0.2v
解:B球速度的最小值发生在完全非弹性碰撞情形
由动量守恒:
B球速度的最大值发生在弹性碰撞时:
∵所以,只有0.4v是速度可能值
复习动量守恒定律:
就两个物体组成的系统:
或
系统不受外力或所受外力之和为零
作用时间极短,外力远小于内力
某方向不受外力,则系统在该方向动量守恒
理想守恒:
近似守恒:
单方向守恒:
动量守恒条件:
1.5 动量守恒定律应用(2)
---- 弹性碰撞和非弹性碰撞
物理选修1第一章:
一、生活中的碰撞:
最早发表有关碰撞问题研究成果的是布拉格大学校长、物理学教授马尔西(1595—1667),他在1639年发表的《运动的比例》中得出一些碰撞的结论。随后著名的物理学家如伽利略、马略特、牛顿、笛卡尔、惠更斯等都先后进行了一系列的实验总结出碰撞规律,为动量守恒定律的建立奠定了基础。
碰撞:
相对运动的物体相遇在极短时间内通过相互作用,
运动状态发生了明显变化的过程
范围:
宏观物体间的碰撞:
如星体撞击、列车相撞、球相撞
微观物体间的碰撞:
如电子碰撞、粒子轰击原子核等
即使是很小的物体,当运动速度变化很快时,瞬时力可以达到惊人的程度。有关资料介绍,一只重17.8N的飞鸟与运动着的飞机相撞,如果飞机速度是800km/h,碰撞力可高达3.56 105N,即为鸟重的2 104 倍!
一、生活中的碰撞:
不利因素:由于碰撞会损坏机械、仪器等物品。
有利方面:利用碰撞进行工作,如锻打金属,打桩等。
【方案1】 实验测量,间接验证
θ2
θ1
v
v0
θ1→h1→v0→ mv02/2
θ2→h2→v→ 2mv2/2
θ
θ
【设问】如何探寻两球碰撞前后有无机械能损失?
看两次摆角是否相同
上节课分析我们知道,在合外力为零或者内力远大于外力的情况下,两个物体碰撞过程遵守动量守恒,那么,碰撞过程中能量是否守恒呢?
由动量守恒定律:
碰撞前系统总动能:
碰撞后系统总动能:
碰撞过程中有机械能损失
【方案2】 :理论论证:
v
v0
m
2m
m
v1
v共
弹性碰撞
非弹性碰撞
完全非
弹性碰撞
二、碰撞的分类:
分类方式一:从能量变化角度分
碰撞过程中机械能守恒
碰撞过程中机械能不守恒
碰撞后粘在一起,以共同速度运动
1、弹性碰撞:
2、非弹性碰撞:
3、完全非弹性碰撞:
机械能损失最大!
碰撞过程中能量与形变量的演变:
【★讨论问题】
一维弹性碰撞的碰后速度的确定?
v1
v1/
m1
v2/
m2
m1
m2
(对心碰撞、正碰)
质量相等的两物体弹性碰撞后 交换速度
若A、B两物分别以v1、v2运动 则
质量相等的两物体弹性
碰撞后交换速度仍成立
θ
θ
例1、在光滑水平面上,动能为E0、动量的大小为P0的小钢球1与静止的小钢球2发生碰撞,碰撞前后球1的运动方向相反,将碰撞后球1的动能和动量的大小分别记为E1、P1,球2的动能和动量的大小分别记为E2、P2,则必有:
A、E1
1、动量制约
2、动能制约
3、运动制约
——不增
——合理
碰撞规律总结
—— 守恒
二、碰撞的分类:
分类方式二:从碰撞速度方向分
1、对心碰撞——正碰:
2、非对心碰撞——斜碰:
碰前运动速度与两球心连线处于同一直线上,碰后,两球仍沿这条直线
碰前运动速度与两球心连线不在同一直线上,碰后,两球速度都会偏离原来两球的连线
3、散射:
中子的发现:1932年查德威克(英国)
中子减速剂:石墨、重水
微观世界碰撞现象简单介绍:
碰撞特点
相互作用时间极短;
平均作用力(内力)很大
系统所受外力之和通常远小于内力,可忽略。
宏观物体碰撞前后的位置可认为不变
系统总动能不可能增加,即:E K前≥E K后
因此,系统动量近似守恒
碰撞分类
弹性碰撞 →动量、机械能守恒
非弹性碰撞 →动量守恒、机械能有损失
完全非弹性碰撞 →动量守恒、机械能损失最大
对心碰撞(正碰)→碰撞前后速度沿球心连线
非对心碰撞(斜碰)→碰撞前后速度不共线
小结:
例3、质量为m速度为v的A球,跟质量为3m的静止B球发生正碰,碰撞可能是弹性,也可能非弹性,碰后B球的速度可能是以下值吗?
(A)0.6v (B)0.4v (C)0.2v
解:B球速度的最小值发生在完全非弹性碰撞情形
由动量守恒:
B球速度的最大值发生在弹性碰撞时:
∵所以,只有0.4v是速度可能值
