2023年中考数学复习: 二次函数训练 (含答案)
文档属性
| 名称 | 2023年中考数学复习: 二次函数训练 (含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 432.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-13 07:20:14 | ||
图片预览


文档简介
2023年中考数学复习: 二次函数
班级:_________ 姓名:_________ 学号:__________
选择题(本大题共10小题,在每小题列出的选项中,选出符合题目的一项)
1.抛物线的顶点坐标是( )
A. B. C. D.
2.把抛物线向右平移个单位,再向下平移个单位,得到抛物线( )
A. B.
C. D.
3.长为,宽为的矩形,四个角上剪去边长为的小正方形,然后把四边折起来,作成底面为的无盖的长方体盒子,则y与x的关系式为( )
A. B.
C. D.
4.若二次函数y=ax2+bx+c的x与y的部分对应值如下表:则下列说法错误的是( )
x … -1 0 1 2 3 …
y … …
A.二次函数图像与x轴交点有两个
B.x≥2时y随x的增大而增大
C.二次函数图像与x轴交点横坐标一个在-1~0之间,另一个在2~3之间
D.对称轴为直线x=1.5
5.已知点都在抛物线上,点A在点B左侧,下列选项正确的是( )
A.若,则 B.若,则
C.若,则 D.若,则
6.如图,抛物线与直线相交于点和,若,则的取值范围是( )
A. B. C.或 D.或
7.已知二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,对称轴为,且经过点(-1,0).下列结论:①3a+b=0;②若点,(3,y2)是抛物线上的两点,则y1A.1个 B.2个 C.3个 D.4个
8.已知实数a,b满足,则代数式的最小值等于( )
A.5 B.4 C.3 D.2
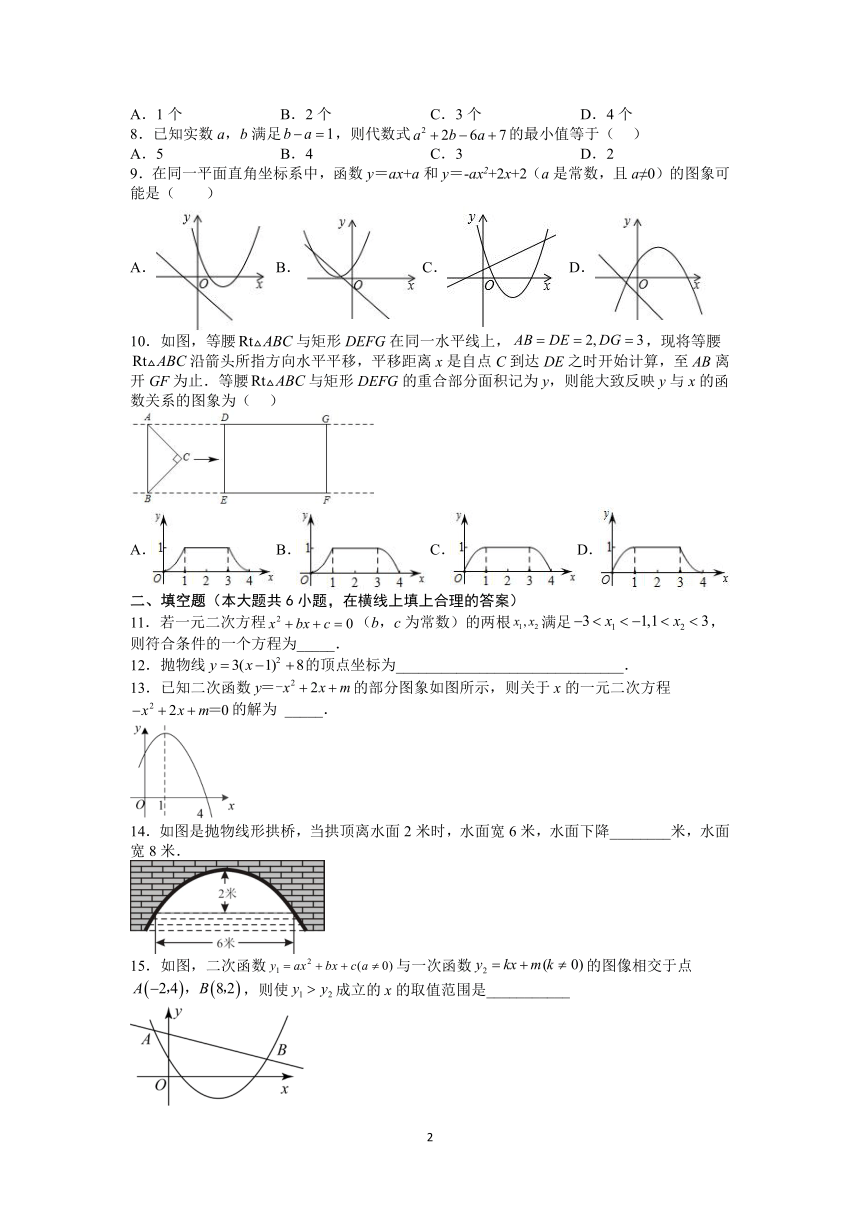
9.在同一平面直角坐标系中,函数y=ax+a和y=-ax2+2x+2(a是常数,且a≠0)的图象可能是( )
A.B.C.D.
10.如图,等腰与矩形DEFG在同一水平线上,,现将等腰沿箭头所指方向水平平移,平移距离x是自点C到达DE之时开始计算,至AB离开GF为止.等腰与矩形DEFG的重合部分面积记为y,则能大致反映y与x的函数关系的图象为( )
A.B.C.D.
二、填空题(本大题共6小题,在横线上填上合理的答案)
11.若一元二次方程(b,c为常数)的两根满足,则符合条件的一个方程为_____.
12.抛物线的顶点坐标为______________________________.
13.已知二次函数的部分图象如图所示,则关于x的一元二次方程的解为 _____.
14.如图是抛物线形拱桥,当拱顶离水面2米时,水面宽6米,水面下降________米,水面宽8米.
15.如图,二次函数与一次函数的图像相交于点,则使成立的x的取值范围是___________
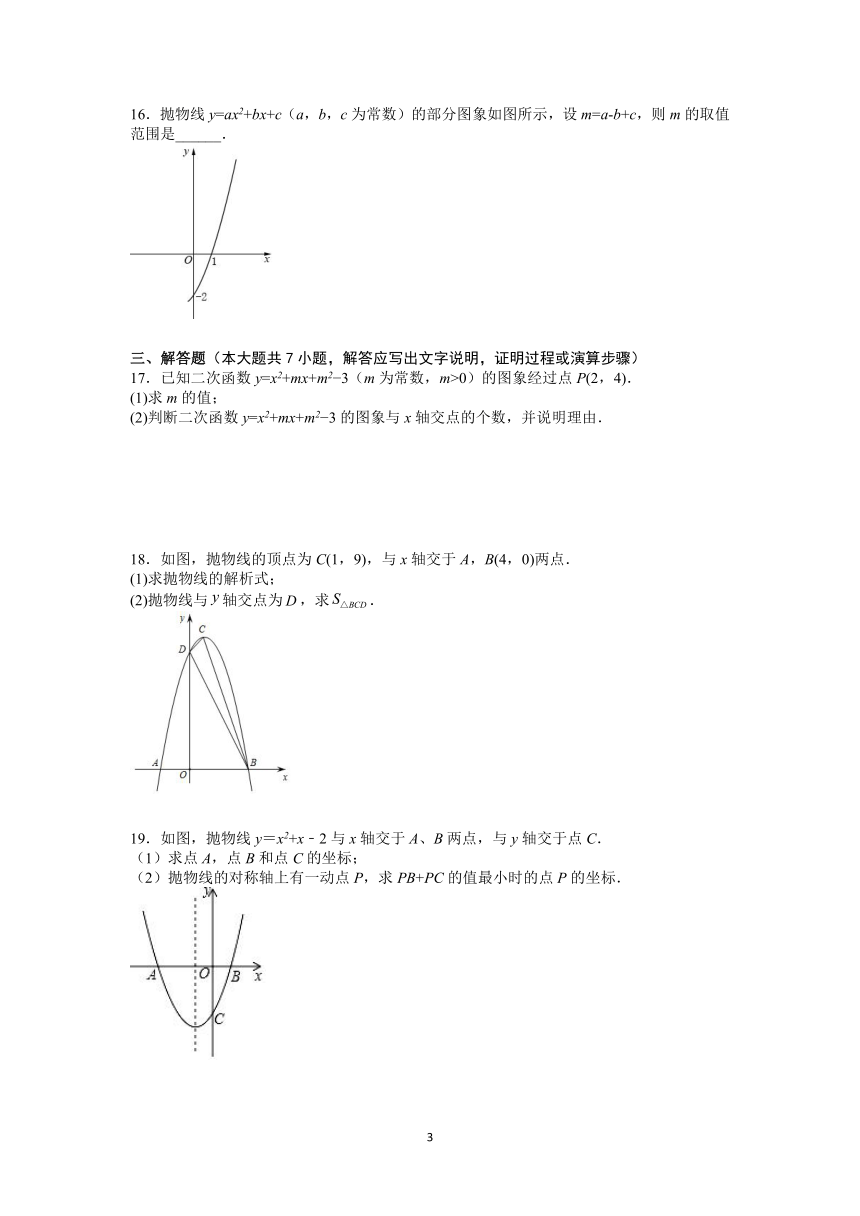
16.抛物线y=ax2+bx+c(a,b,c为常数)的部分图象如图所示,设m=a-b+c,则m的取值范围是______.
三、解答题(本大题共7小题,解答应写出文字说明,证明过程或演算步骤)
17.已知二次函数y=x2+mx+m2 3(m为常数,m>0)的图象经过点P(2,4).
(1)求m的值;
(2)判断二次函数y=x2+mx+m2 3的图象与x轴交点的个数,并说明理由.
18.如图,抛物线的顶点为C(1,9),与x轴交于A,B(4,0)两点.
(1)求抛物线的解析式;
(2)抛物线与轴交点为,求.
19.如图,抛物线y=x2+x﹣2与x轴交于A、B两点,与y轴交于点C.
(1)求点A,点B和点C的坐标;
(2)抛物线的对称轴上有一动点P,求PB+PC的值最小时的点P的坐标.
20.合肥某商场购进一批新型网红玩具.已知这种玩具进价为17元/件,且该玩具的月销售量y(件)与销售单价x(元)之间满足一次函数关系,下表是月销售量与销售单价的几组对应关系:
销售单价x/元 20 25 30 35
月销售量y/件 3300 2800 2300 1800
(1)求y关于x的函数关系式;
(2)当销售单价为多少元时,月销售利润最大,最大利润是多少?
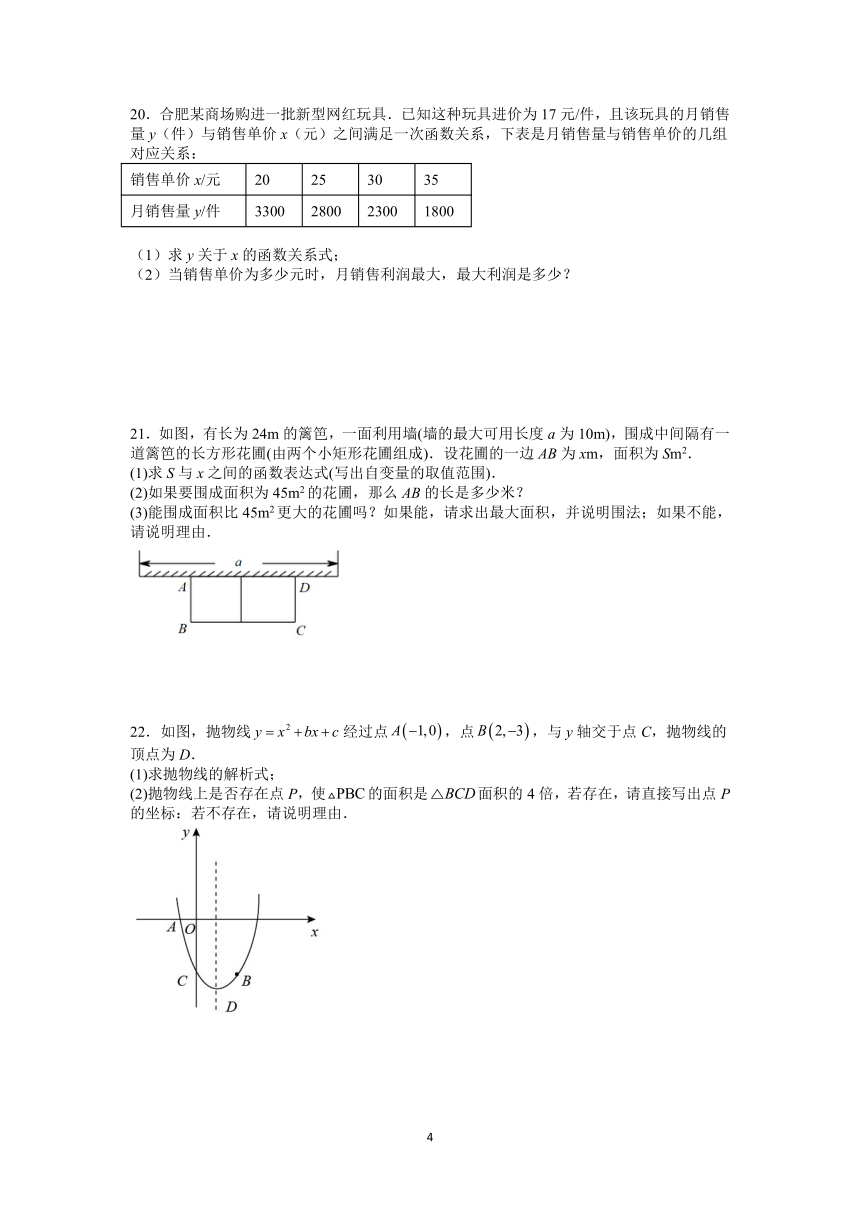
21.如图,有长为24m的篱笆,一面利用墙(墙的最大可用长度a为10m),围成中间隔有一道篱笆的长方形花圃(由两个小矩形花圃组成).设花圃的一边AB为xm,面积为Sm2.
(1)求S与x之间的函数表达式(写出自变量的取值范围).
(2)如果要围成面积为45m2的花圃,那么AB的长是多少米?
(3)能围成面积比45m2更大的花圃吗?如果能,请求出最大面积,并说明围法;如果不能,请说明理由.
22.如图,抛物线经过点,点,与y轴交于点C,抛物线的顶点为D.
(1)求抛物线的解析式;
(2)抛物线上是否存在点P,使的面积是面积的4倍,若存在,请直接写出点P的坐标:若不存在,请说明理由.
23.如图,在平面直角坐标系中,抛物线(a≠0)的图象与x轴交于A、C两点,与y轴交于点B,其中点B坐标为(0,-4),点C坐标为(2,0).
(1)求此抛物线的函数解析式.
(2)点D是直线AB下方抛物线上一个动点,连接AD、BD,探究是否存在点D,使得△ABD的面积最大?若存在,请求出点D的坐标;若不存在,请说明理由.
(3)点P为该抛物线对称轴上的动点,使得△PAB为直角三角形,请求出点P的坐标.
答案:
1.A 2.C 3.C 4.D 5.D 6.C 7.C 8.A 9.B 10.B
11.(答案不唯一) 12.(1,8) 13. 14.
15.或 16.
17(1)解:∵二次函数y= x2+mx+m2 3图象经过点P(2,4) ,
∴4=4+2m+m2 3,
即m2+2m 3=0,
解得:m1=1,m2= 3,
又∵m>0,
∴m=1;
(2)解:由(1)知二次函数y=x2+x 2,
∵Δ=b2 4ac=12+8=9>0,
∴二次函数y=x2+x 2的图象与x轴有两个交点.
18.(1)解:∵抛物线的顶点为C(1,9),
∴设抛物线的解析式为y=a(x-1)2+9,
∵抛物线与x轴交于点B(4,0),
∴a(4-1)2+9=0,
解得:a=-1,
∴抛物线的解析式为y=-(x-1)2+9=-x2+2x+8;
(2)解:过点C作CE⊥y轴于点E,
∵抛物线与y轴交点为D,
∴D(0,8),
∵B(4,0),C(1,9),
∴CE=1,OE=9,OD=8,OB=4,
∴S△BCD= S梯形OBCE-S△ECD-S△OBD
=(1+4)×9-×1×1-×4×8
=6.
19.解:(1)由 y=0,得 x2+x-2=0 解得 x=-2,x=1,
∴A(-2,0),B(1,0),
由 x=0,得 y=-2,
∴C(0,-2).
(2)连接AC与对称轴的交点即为点P.
设直线 AC 为 y=kx+b,
则﹣2k+b=0,b=﹣2:
得 k=﹣1,
y=﹣x﹣2.
对称轴为 x=,
当 x=时,
y=-2=,
∴P(,).
20.(1)设y关于x的函数关系式为y=kx+b(k≠0)
由题意得:
解得:
∴y关于x的函数关系式为y=﹣100x+5300.
(2)设月销售利润为w元,
则w=(x﹣17)(﹣100x+5300)
=﹣100x2+7000x﹣90100
=﹣100(x﹣35)2+32400
∵﹣100<0
∴当x=35时,w有最大值,最大值为32400.
答:当销售单价为35元时,月销售利润最大,最大利润是32400元.
21.解:(1) ∵0<24 3x≤10,
∴≤x<8
∴S=x(24-3x)=-3x2+24x(≤x<8).
(2)当S=45时,有-3x2+24x=45.
解得x1=3,x2=5.
∵≤x<8,
∴x=5,
即AB的长为5m.
(3)能围成面积比45m2更大的花圃.
∵S=-3x2+24x=-3(x-4)2+48,其函数图象开口向下,对称轴为直线x=4,当x>4时,y随x的增大而减小,
∴在≤x<8的范围内,当x=时,S取得最大值,S最大值=.
即最大面积为m2,
此时AB=m,BC=10m.
22.(1)解:∵抛物线过点,点,
∴,
解得,
∴抛物线的解析式为:.
(2)解:存在.
∵,
∴,
将代入得,,
∴,
又∵B(2,-3),
∴BC//x轴,
∴到线段的距离为1,,
∴,
∴,
设,由题意可知点P在直线BC上方,
则,
整理得,,
解得,或,
∴,,
∴存在点P,使的面积是面积的4倍,点P的坐标为,.
23.(1)解:将B(0,-4),C(2,0)代入,
得:,
解得:,
∴抛物线的函数解析式为:.
(2)向下平移直线AB,使平移后的直线与抛物线只有唯一公共点D时,此时点D到直线AB的距离最大,此时△ABD的面积最大,
∵时,,,
∴A点坐标为:(-4,0),
设直线AB关系式为:,
将A(-4,0),B(0,-4),代入,
得:,
解得:,
∴直线AB关系式为:,
设直线AB平移后的关系式为:,
则方程有两个相等的实数根,
即有两个相等的实数根,
∴,
即的解为:x=-2,
将x=-2代入抛物线解析式得,,
∴点D的坐标为:(-2,-4)时,△ABD的面积最大;
(3)①当∠PAB=90°时,
即PA⊥AB,则设PA所在直线解析式为:,
将A(-4,0)代入得,,
解得:,
∴PA所在直线解析式为:,
∵抛物线对称轴为:x=-1,
∴当x=-1时,,
∴P点坐标为:(-1,3);
②当∠PBA=90°时,
即PB⊥AB,则设PB所在直线解析式为:,
将B(0,-4)代入得,,
∴PA所在直线解析式为:,
∴当x=-1时,,
∴P点坐标为:(-1,-5);
③当∠APB=90°时,设P点坐标为:,
∴PA所在直线斜率为:,PB在直线斜率为:,
∵PA⊥PB,
∴=-1,
解得:,,
∴P点坐标为:,
综上所述,P点坐标为:(-1,3),(-1,-5),,时,△PAB为直角三角形.
班级:_________ 姓名:_________ 学号:__________
选择题(本大题共10小题,在每小题列出的选项中,选出符合题目的一项)
1.抛物线的顶点坐标是( )
A. B. C. D.
2.把抛物线向右平移个单位,再向下平移个单位,得到抛物线( )
A. B.
C. D.
3.长为,宽为的矩形,四个角上剪去边长为的小正方形,然后把四边折起来,作成底面为的无盖的长方体盒子,则y与x的关系式为( )
A. B.
C. D.
4.若二次函数y=ax2+bx+c的x与y的部分对应值如下表:则下列说法错误的是( )
x … -1 0 1 2 3 …
y … …
A.二次函数图像与x轴交点有两个
B.x≥2时y随x的增大而增大
C.二次函数图像与x轴交点横坐标一个在-1~0之间,另一个在2~3之间
D.对称轴为直线x=1.5
5.已知点都在抛物线上,点A在点B左侧,下列选项正确的是( )
A.若,则 B.若,则
C.若,则 D.若,则
6.如图,抛物线与直线相交于点和,若,则的取值范围是( )
A. B. C.或 D.或
7.已知二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,对称轴为,且经过点(-1,0).下列结论:①3a+b=0;②若点,(3,y2)是抛物线上的两点,则y1
8.已知实数a,b满足,则代数式的最小值等于( )
A.5 B.4 C.3 D.2
9.在同一平面直角坐标系中,函数y=ax+a和y=-ax2+2x+2(a是常数,且a≠0)的图象可能是( )
A.B.C.D.
10.如图,等腰与矩形DEFG在同一水平线上,,现将等腰沿箭头所指方向水平平移,平移距离x是自点C到达DE之时开始计算,至AB离开GF为止.等腰与矩形DEFG的重合部分面积记为y,则能大致反映y与x的函数关系的图象为( )
A.B.C.D.
二、填空题(本大题共6小题,在横线上填上合理的答案)
11.若一元二次方程(b,c为常数)的两根满足,则符合条件的一个方程为_____.
12.抛物线的顶点坐标为______________________________.
13.已知二次函数的部分图象如图所示,则关于x的一元二次方程的解为 _____.
14.如图是抛物线形拱桥,当拱顶离水面2米时,水面宽6米,水面下降________米,水面宽8米.
15.如图,二次函数与一次函数的图像相交于点,则使成立的x的取值范围是___________
16.抛物线y=ax2+bx+c(a,b,c为常数)的部分图象如图所示,设m=a-b+c,则m的取值范围是______.
三、解答题(本大题共7小题,解答应写出文字说明,证明过程或演算步骤)
17.已知二次函数y=x2+mx+m2 3(m为常数,m>0)的图象经过点P(2,4).
(1)求m的值;
(2)判断二次函数y=x2+mx+m2 3的图象与x轴交点的个数,并说明理由.
18.如图,抛物线的顶点为C(1,9),与x轴交于A,B(4,0)两点.
(1)求抛物线的解析式;
(2)抛物线与轴交点为,求.
19.如图,抛物线y=x2+x﹣2与x轴交于A、B两点,与y轴交于点C.
(1)求点A,点B和点C的坐标;
(2)抛物线的对称轴上有一动点P,求PB+PC的值最小时的点P的坐标.
20.合肥某商场购进一批新型网红玩具.已知这种玩具进价为17元/件,且该玩具的月销售量y(件)与销售单价x(元)之间满足一次函数关系,下表是月销售量与销售单价的几组对应关系:
销售单价x/元 20 25 30 35
月销售量y/件 3300 2800 2300 1800
(1)求y关于x的函数关系式;
(2)当销售单价为多少元时,月销售利润最大,最大利润是多少?
21.如图,有长为24m的篱笆,一面利用墙(墙的最大可用长度a为10m),围成中间隔有一道篱笆的长方形花圃(由两个小矩形花圃组成).设花圃的一边AB为xm,面积为Sm2.
(1)求S与x之间的函数表达式(写出自变量的取值范围).
(2)如果要围成面积为45m2的花圃,那么AB的长是多少米?
(3)能围成面积比45m2更大的花圃吗?如果能,请求出最大面积,并说明围法;如果不能,请说明理由.
22.如图,抛物线经过点,点,与y轴交于点C,抛物线的顶点为D.
(1)求抛物线的解析式;
(2)抛物线上是否存在点P,使的面积是面积的4倍,若存在,请直接写出点P的坐标:若不存在,请说明理由.
23.如图,在平面直角坐标系中,抛物线(a≠0)的图象与x轴交于A、C两点,与y轴交于点B,其中点B坐标为(0,-4),点C坐标为(2,0).
(1)求此抛物线的函数解析式.
(2)点D是直线AB下方抛物线上一个动点,连接AD、BD,探究是否存在点D,使得△ABD的面积最大?若存在,请求出点D的坐标;若不存在,请说明理由.
(3)点P为该抛物线对称轴上的动点,使得△PAB为直角三角形,请求出点P的坐标.
答案:
1.A 2.C 3.C 4.D 5.D 6.C 7.C 8.A 9.B 10.B
11.(答案不唯一) 12.(1,8) 13. 14.
15.或 16.
17(1)解:∵二次函数y= x2+mx+m2 3图象经过点P(2,4) ,
∴4=4+2m+m2 3,
即m2+2m 3=0,
解得:m1=1,m2= 3,
又∵m>0,
∴m=1;
(2)解:由(1)知二次函数y=x2+x 2,
∵Δ=b2 4ac=12+8=9>0,
∴二次函数y=x2+x 2的图象与x轴有两个交点.
18.(1)解:∵抛物线的顶点为C(1,9),
∴设抛物线的解析式为y=a(x-1)2+9,
∵抛物线与x轴交于点B(4,0),
∴a(4-1)2+9=0,
解得:a=-1,
∴抛物线的解析式为y=-(x-1)2+9=-x2+2x+8;
(2)解:过点C作CE⊥y轴于点E,
∵抛物线与y轴交点为D,
∴D(0,8),
∵B(4,0),C(1,9),
∴CE=1,OE=9,OD=8,OB=4,
∴S△BCD= S梯形OBCE-S△ECD-S△OBD
=(1+4)×9-×1×1-×4×8
=6.
19.解:(1)由 y=0,得 x2+x-2=0 解得 x=-2,x=1,
∴A(-2,0),B(1,0),
由 x=0,得 y=-2,
∴C(0,-2).
(2)连接AC与对称轴的交点即为点P.
设直线 AC 为 y=kx+b,
则﹣2k+b=0,b=﹣2:
得 k=﹣1,
y=﹣x﹣2.
对称轴为 x=,
当 x=时,
y=-2=,
∴P(,).
20.(1)设y关于x的函数关系式为y=kx+b(k≠0)
由题意得:
解得:
∴y关于x的函数关系式为y=﹣100x+5300.
(2)设月销售利润为w元,
则w=(x﹣17)(﹣100x+5300)
=﹣100x2+7000x﹣90100
=﹣100(x﹣35)2+32400
∵﹣100<0
∴当x=35时,w有最大值,最大值为32400.
答:当销售单价为35元时,月销售利润最大,最大利润是32400元.
21.解:(1) ∵0<24 3x≤10,
∴≤x<8
∴S=x(24-3x)=-3x2+24x(≤x<8).
(2)当S=45时,有-3x2+24x=45.
解得x1=3,x2=5.
∵≤x<8,
∴x=5,
即AB的长为5m.
(3)能围成面积比45m2更大的花圃.
∵S=-3x2+24x=-3(x-4)2+48,其函数图象开口向下,对称轴为直线x=4,当x>4时,y随x的增大而减小,
∴在≤x<8的范围内,当x=时,S取得最大值,S最大值=.
即最大面积为m2,
此时AB=m,BC=10m.
22.(1)解:∵抛物线过点,点,
∴,
解得,
∴抛物线的解析式为:.
(2)解:存在.
∵,
∴,
将代入得,,
∴,
又∵B(2,-3),
∴BC//x轴,
∴到线段的距离为1,,
∴,
∴,
设,由题意可知点P在直线BC上方,
则,
整理得,,
解得,或,
∴,,
∴存在点P,使的面积是面积的4倍,点P的坐标为,.
23.(1)解:将B(0,-4),C(2,0)代入,
得:,
解得:,
∴抛物线的函数解析式为:.
(2)向下平移直线AB,使平移后的直线与抛物线只有唯一公共点D时,此时点D到直线AB的距离最大,此时△ABD的面积最大,
∵时,,,
∴A点坐标为:(-4,0),
设直线AB关系式为:,
将A(-4,0),B(0,-4),代入,
得:,
解得:,
∴直线AB关系式为:,
设直线AB平移后的关系式为:,
则方程有两个相等的实数根,
即有两个相等的实数根,
∴,
即的解为:x=-2,
将x=-2代入抛物线解析式得,,
∴点D的坐标为:(-2,-4)时,△ABD的面积最大;
(3)①当∠PAB=90°时,
即PA⊥AB,则设PA所在直线解析式为:,
将A(-4,0)代入得,,
解得:,
∴PA所在直线解析式为:,
∵抛物线对称轴为:x=-1,
∴当x=-1时,,
∴P点坐标为:(-1,3);
②当∠PBA=90°时,
即PB⊥AB,则设PB所在直线解析式为:,
将B(0,-4)代入得,,
∴PA所在直线解析式为:,
∴当x=-1时,,
∴P点坐标为:(-1,-5);
③当∠APB=90°时,设P点坐标为:,
∴PA所在直线斜率为:,PB在直线斜率为:,
∵PA⊥PB,
∴=-1,
解得:,,
∴P点坐标为:,
综上所述,P点坐标为:(-1,3),(-1,-5),,时,△PAB为直角三角形.
同课章节目录
