19.2.2 第2课时 一次函数图象与性质 课件(共25张PPT)
文档属性
| 名称 | 19.2.2 第2课时 一次函数图象与性质 课件(共25张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 38.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-12 08:20:39 | ||
图片预览




文档简介
(共25张PPT)
一次函数的图象和性质
19.2.2 一次函数
| 第2课时|
情景引入
一次函数的图象和性质
一次函数图象与正比例图象有什么联系?
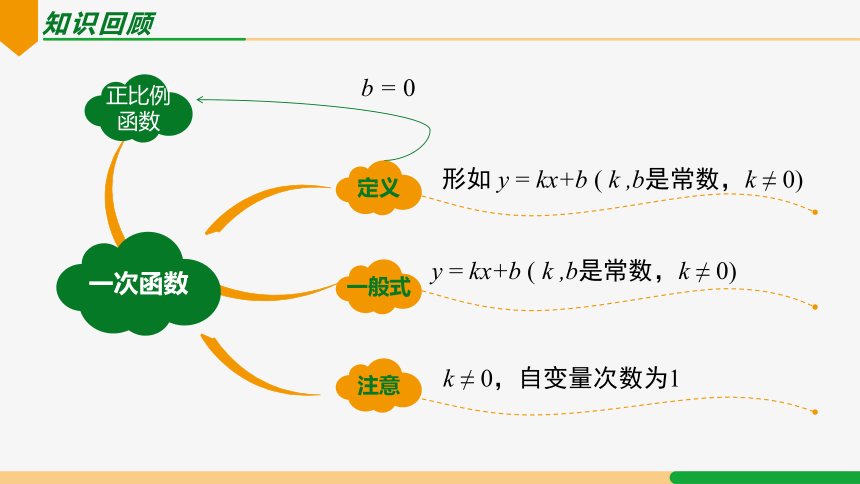
知识回顾
正比例
函数
注意
一般式
一次函数
形如 y = kx+b ( k ,b是常数,k ≠ 0)
y = kx+b ( k ,b是常数,k ≠ 0)
k ≠ 0,自变量次数为1
b = 0
定义
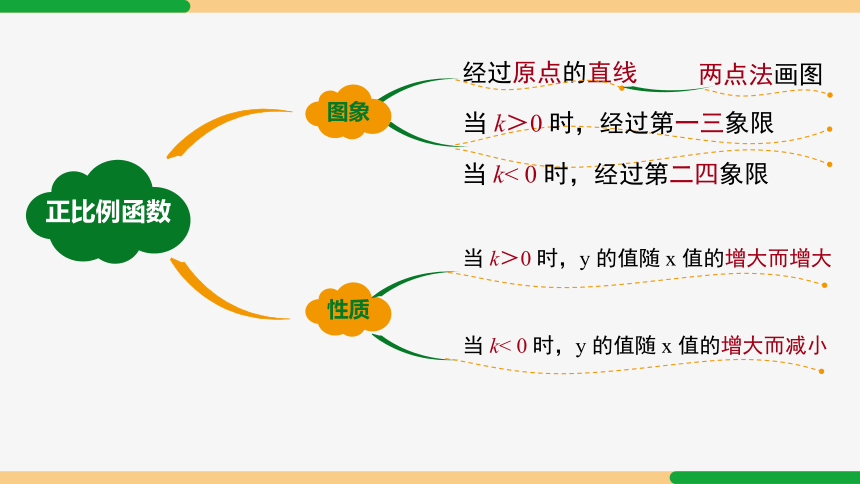
两点法画图
经过原点的直线
图象
性质
正比例函数
当 k>0 时,经过第一三象限
当 k< 0 时,经过第二四象限
当 k>0 时,y 的值随 x 值的增大而增大
当 k< 0 时,y 的值随 x 值的增大而减小
新知探究
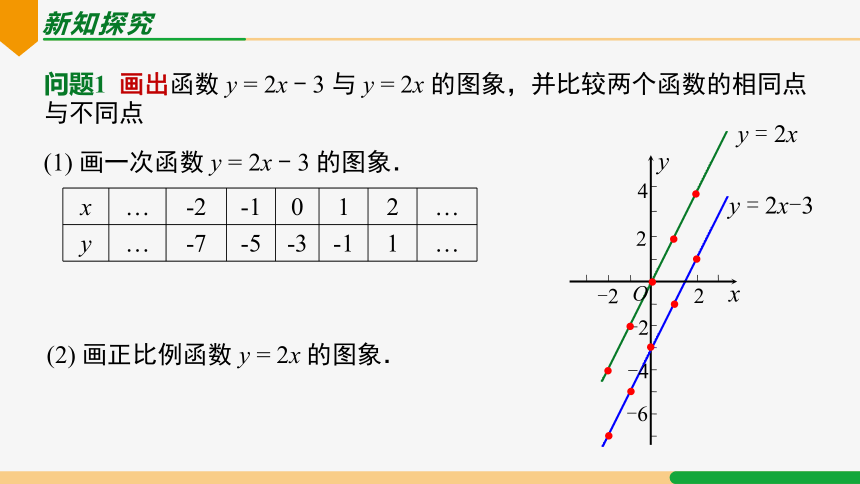
问题1 画出函数 y = 2x - 3 与 y = 2x 的图象,并比较两个函数的相同点与不同点
x … -2 -1 0 1 2 …
y … -7 -5 -3 -1 1 …
(1) 画一次函数 y = 2x - 3 的图象.
(2) 画正比例函数 y = 2x 的图象.
2
-2
-4
-6
-2
2
x
y
O
y = 2x-3
y = 2x
4
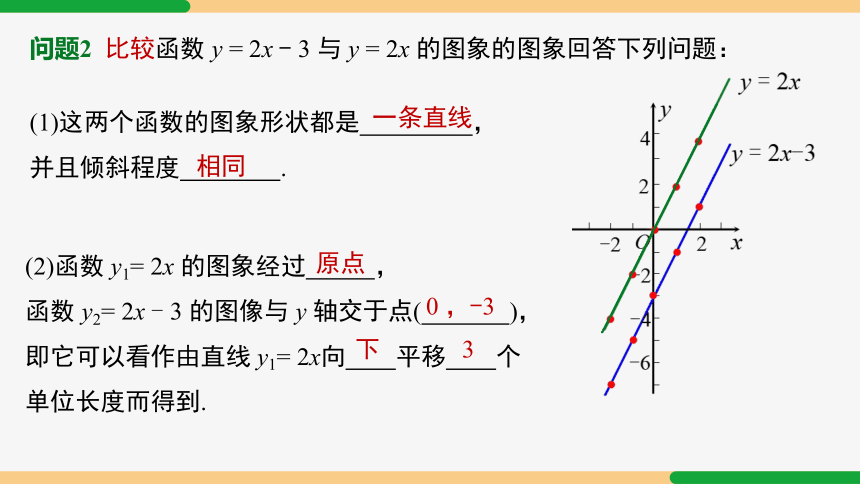
(2)函数 y1= 2x 的图象经过 ,
函数 y2= 2x - 3 的图像与 y 轴交于点( ),即它可以看作由直线 y1= 2x向 平移 个单位长度而得到.
(1)这两个函数的图象形状都是 ,
并且倾斜程度 .
原点
0 ,-3
下
3
一条直线
相同
问题2 比较函数 y = 2x - 3 与 y = 2x 的图象的图象回答下列问题:
向上平移
3 个单位
向上平移
3 个单位
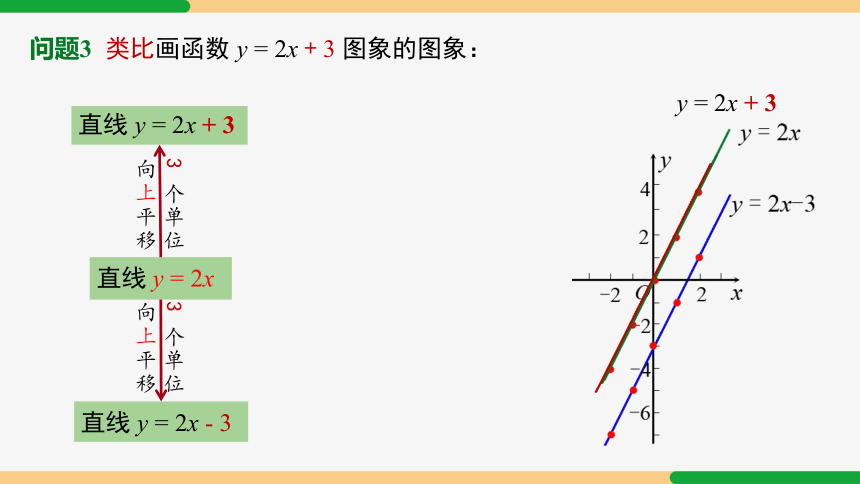
问题3 类比画函数 y = 2x + 3 图象的图象:
直线 y = 2x
直线 y = 2x + 3
直线 y = 2x - 3
y = 2x + 3
1
y
x
o
5
-6
-1
问题4 推广应用
在同一直角坐标系画一次函数 y = - 6x 与 y = - 6x + 5 的图象.
(3) 一次函数 y = - 6x + 5 的图象可以看作由直线y = - 6x 向 平移 个单位长度而得到.与 y 轴交于点 ,
上
5
(0,5)
平行
y = -6x+5
y = -6x
(1)这两个函数的图象形状都是 ,
并且倾斜程度 .
一条直线
相同
(2) 在同一直角坐标系中,直线 y = - 6x 与 y = - 6x + 5 的位置关系是 ______
知识要点1
一次函数的图象
1. 一次函数 y = kx+b (k ≠ 0) 的图象是一条直线,我们称它为直线 y = kx+b (k ≠ 0).
向上(或下)平移
|b| 个单位长度
2.直线 y = kx y = kx+b
(1)b>0 时,向上平移;
(2)b<0 时,向下平移.)
典例讲解
例1 用你认为最简单的方法画出下列函数的图象:
(1) y = -2x - 1;(2) y = 0.5x + 1
x 0 1
y = - 2x - 1
y = 0.5x + 1
-1
-3
1
1.5
也可以先画直线 y = -2x 与 y = 0.5x,再分别平移它们,也能得到直线y = -2x - 1与 y = 0.5x + 1.
y = -2x-1
y = 0.5x+1
方法一:两点法
方法二:平移法
(1) y = x + 1; (2) y = 2x + 1;
(3) y = -x + 1; (4) y = -2x + 1.
问题2 联想一次函数解析式 y = kx+b (k ≠ 0) k 的正负对函数图象有什么影响?
问题1 画出下列一次函数的图象。
y
x
O
1
1
-1
y = x+1
y = 2x+1
y = -x+1
y = -2x+1
当 k>0 时,经过第一三象限
当 k< 0 时,经过第二四象限
知识要点2
一次函数的图象与性质
当 k>0 时,y 的值随 x 值的增大而增大
当 k< 0 时,y 的值随 x 值的增大而减小
针对练习
1. 一次函数 y = x - 2 的大致图象为( )
C
A B C D
2.下列函数中,y 的值随 x 值的增大而增大的函数是( )
A. y = - 2x B. y = - 2x + 1
C. y = x - 2 D. y = - x - 2
C
y
x
o
y
x
o
y
x
o
y
x
o
典例讲解
例2 已知直线y=(1-3k )x+2k-1.
(1)k 为何值时,直线与y 轴交点的纵坐标是-2?
(2)k 为何值时,直线经过第二、三、四象限?
(3)k 为何值时,已知直线与直线 y=-3x-5平行?
(1)当x=0时,y=-2,
即当2k-1=-2,k= 时,直线与y 轴交点的纵坐标是-2.
(2)当 直线经过第二、三、四象限.
(3)当1-3k=-3,即当 时,2k-1= ≠-5,
此时,已知直线与直线 y=-3x-5平行.
解:
例2 P1(x1,y1),P2(x2,y2)是一次函数 y = - 0.5x + 3 图象上的两点,下列判断中,正确的是( )
A. y1>y2 C. 当 x1<x2 时,y1<y2
B. y1<y2 D. 当 x1<x2 时,y1>y2
D
两点法画图
课堂小结
图象
性质
一次函数
当 k>0 时,经过第一三象限
当 k< 0 时,经过第二四象限
当 k>0 时,y 的值随 x 值的增大而增大
当 k< 0 时,y 的值随 x 值的增大而减小
正比例函数
平移
一次函数y = kx+b (k ≠ 0) k ,b与函数图象
k 0,b 0
>
>
k 0,b 0
k 0,b 0
>
>
<
=
k 0,b 0
k 0,b 0
k 0,b 0
>
<
<
<
<
=
y
x
o
y
x
o
y
x
o
y
x
o
y
x
o
y
x
o
课堂练习
1.在平面直角坐标系中,一次函数 y=x-1的图象是( )
B
2.将一次函数 y=2x-3的图象沿y 轴向上平移8个单位长度,所得直线对应的函数解析式为( )
A.y=2x-5 B.y=2x+5
C.y=2x+8 D.y=2x-8
B
3.一次函数 y=(m-2)x+3的图象如图所示,则m 的取值范围是( )
A.m<2 B.0<m<2
C.m<0 D.m>2
A
4.已知点(-1,y1),(4,y2)在一次函数y=3x-2的图象上,则y1,y2,0的大小关系是( )
A.0<y1<y2 B.y1<0<y2
C.y1<y2<0 D.y2<0<y1
B
5.直线 y = 2x - 3 与 x 轴交点的坐标为________;与 y 轴交点的坐标为_______;图象经过第__________象限, y 随 x 的增大而________.
6. 若直线 y = kx + 2 与 y = 3x - 1平行,则 k = .
3
(0,-3)
一、三、四
增大
(1.5,0)
7 已知直线 y=(2m+4)x+m-3,求:
(1)当m 为何值时,y 随x 的增大而增大?
(2)当m 为何值时,图象与y 轴的交点在x 轴下方?
(3)当m 为何值时,函数图象经过原点?
(4)当m 为何值时,这条直线平行于直线y=-x?
(1)2m+4>0,∴m>-2.
(2)m-3<0,∴m<3.
(3)m-3=0,∴m=3.
(4)2m+4=-1,∴m=- .
8 平面直角坐标系xOy 中,点P 的坐标为(m+1,m-1).
(1)试判断点P 是否在一次函数y=x-2的图象上,并 说明理由;
(2)如图,一次函数y=- x+3的图象与x 轴、y 轴分 别相交于A、B,若点P 在△AOB 的内部,求m 的取值范围.
(1)∵当x=m+1时,y=m+1-2=m-1,
∴点P (m+1,m-1)在函数 y=x-2的图象上.
(2)∵函数 y=- x+3,∴A (6,0),B (0,3).
∵点P 在△AOB 的内部,
∴0<m+1<6,0<m-1<3,m-1<- (m+1)+3.
∴1<m< .
解:
6. 如图点 P (x,y) 第一象限内一个动点,且在直线 y = - 2x + 8 上,直线与 x 轴交于点 A.
(1) 当点 P 的横坐标为 3 时,△APO 的面积为多少
(2) 设△APO 面积为 S,含 x 的解析式表示 S,并写出 x 的取值范围.
解: (1) ∵令 y = 0,则 - 2x + 8 = 0,解得 x = 4,
∴OA = 4,
∵点 P (x,y) 是第一象限内一个动点,且在直线 y = - 2x + 8 上,
∴当 x = 3 时,y = (-2)×3 + 8 = 2,
∴S△APO = ×4×2 = 4.
6. 如图点 P (x,y) 第一象限内一个动点,且在直线 y = - 2x + 8 上,直线与 x 轴交于点 A.
(2) 设△APO 面积为 S,含 x 的解析式表示 S,并写出 x 的取值范围.
(2)∵点 P (x,-2x + 8),
∴S△APO = OA×(- 2x + 8) = ×4×(-2x + 8)
= - 4x + 16 (0<x<4 ).
一次函数的图象和性质
19.2.2 一次函数
| 第2课时|
情景引入
一次函数的图象和性质
一次函数图象与正比例图象有什么联系?
知识回顾
正比例
函数
注意
一般式
一次函数
形如 y = kx+b ( k ,b是常数,k ≠ 0)
y = kx+b ( k ,b是常数,k ≠ 0)
k ≠ 0,自变量次数为1
b = 0
定义
两点法画图
经过原点的直线
图象
性质
正比例函数
当 k>0 时,经过第一三象限
当 k< 0 时,经过第二四象限
当 k>0 时,y 的值随 x 值的增大而增大
当 k< 0 时,y 的值随 x 值的增大而减小
新知探究
问题1 画出函数 y = 2x - 3 与 y = 2x 的图象,并比较两个函数的相同点与不同点
x … -2 -1 0 1 2 …
y … -7 -5 -3 -1 1 …
(1) 画一次函数 y = 2x - 3 的图象.
(2) 画正比例函数 y = 2x 的图象.
2
-2
-4
-6
-2
2
x
y
O
y = 2x-3
y = 2x
4
(2)函数 y1= 2x 的图象经过 ,
函数 y2= 2x - 3 的图像与 y 轴交于点( ),即它可以看作由直线 y1= 2x向 平移 个单位长度而得到.
(1)这两个函数的图象形状都是 ,
并且倾斜程度 .
原点
0 ,-3
下
3
一条直线
相同
问题2 比较函数 y = 2x - 3 与 y = 2x 的图象的图象回答下列问题:
向上平移
3 个单位
向上平移
3 个单位
问题3 类比画函数 y = 2x + 3 图象的图象:
直线 y = 2x
直线 y = 2x + 3
直线 y = 2x - 3
y = 2x + 3
1
y
x
o
5
-6
-1
问题4 推广应用
在同一直角坐标系画一次函数 y = - 6x 与 y = - 6x + 5 的图象.
(3) 一次函数 y = - 6x + 5 的图象可以看作由直线y = - 6x 向 平移 个单位长度而得到.与 y 轴交于点 ,
上
5
(0,5)
平行
y = -6x+5
y = -6x
(1)这两个函数的图象形状都是 ,
并且倾斜程度 .
一条直线
相同
(2) 在同一直角坐标系中,直线 y = - 6x 与 y = - 6x + 5 的位置关系是 ______
知识要点1
一次函数的图象
1. 一次函数 y = kx+b (k ≠ 0) 的图象是一条直线,我们称它为直线 y = kx+b (k ≠ 0).
向上(或下)平移
|b| 个单位长度
2.直线 y = kx y = kx+b
(1)b>0 时,向上平移;
(2)b<0 时,向下平移.)
典例讲解
例1 用你认为最简单的方法画出下列函数的图象:
(1) y = -2x - 1;(2) y = 0.5x + 1
x 0 1
y = - 2x - 1
y = 0.5x + 1
-1
-3
1
1.5
也可以先画直线 y = -2x 与 y = 0.5x,再分别平移它们,也能得到直线y = -2x - 1与 y = 0.5x + 1.
y = -2x-1
y = 0.5x+1
方法一:两点法
方法二:平移法
(1) y = x + 1; (2) y = 2x + 1;
(3) y = -x + 1; (4) y = -2x + 1.
问题2 联想一次函数解析式 y = kx+b (k ≠ 0) k 的正负对函数图象有什么影响?
问题1 画出下列一次函数的图象。
y
x
O
1
1
-1
y = x+1
y = 2x+1
y = -x+1
y = -2x+1
当 k>0 时,经过第一三象限
当 k< 0 时,经过第二四象限
知识要点2
一次函数的图象与性质
当 k>0 时,y 的值随 x 值的增大而增大
当 k< 0 时,y 的值随 x 值的增大而减小
针对练习
1. 一次函数 y = x - 2 的大致图象为( )
C
A B C D
2.下列函数中,y 的值随 x 值的增大而增大的函数是( )
A. y = - 2x B. y = - 2x + 1
C. y = x - 2 D. y = - x - 2
C
y
x
o
y
x
o
y
x
o
y
x
o
典例讲解
例2 已知直线y=(1-3k )x+2k-1.
(1)k 为何值时,直线与y 轴交点的纵坐标是-2?
(2)k 为何值时,直线经过第二、三、四象限?
(3)k 为何值时,已知直线与直线 y=-3x-5平行?
(1)当x=0时,y=-2,
即当2k-1=-2,k= 时,直线与y 轴交点的纵坐标是-2.
(2)当 直线经过第二、三、四象限.
(3)当1-3k=-3,即当 时,2k-1= ≠-5,
此时,已知直线与直线 y=-3x-5平行.
解:
例2 P1(x1,y1),P2(x2,y2)是一次函数 y = - 0.5x + 3 图象上的两点,下列判断中,正确的是( )
A. y1>y2 C. 当 x1<x2 时,y1<y2
B. y1<y2 D. 当 x1<x2 时,y1>y2
D
两点法画图
课堂小结
图象
性质
一次函数
当 k>0 时,经过第一三象限
当 k< 0 时,经过第二四象限
当 k>0 时,y 的值随 x 值的增大而增大
当 k< 0 时,y 的值随 x 值的增大而减小
正比例函数
平移
一次函数y = kx+b (k ≠ 0) k ,b与函数图象
k 0,b 0
>
>
k 0,b 0
k 0,b 0
>
>
<
=
k 0,b 0
k 0,b 0
k 0,b 0
>
<
<
<
<
=
y
x
o
y
x
o
y
x
o
y
x
o
y
x
o
y
x
o
课堂练习
1.在平面直角坐标系中,一次函数 y=x-1的图象是( )
B
2.将一次函数 y=2x-3的图象沿y 轴向上平移8个单位长度,所得直线对应的函数解析式为( )
A.y=2x-5 B.y=2x+5
C.y=2x+8 D.y=2x-8
B
3.一次函数 y=(m-2)x+3的图象如图所示,则m 的取值范围是( )
A.m<2 B.0<m<2
C.m<0 D.m>2
A
4.已知点(-1,y1),(4,y2)在一次函数y=3x-2的图象上,则y1,y2,0的大小关系是( )
A.0<y1<y2 B.y1<0<y2
C.y1<y2<0 D.y2<0<y1
B
5.直线 y = 2x - 3 与 x 轴交点的坐标为________;与 y 轴交点的坐标为_______;图象经过第__________象限, y 随 x 的增大而________.
6. 若直线 y = kx + 2 与 y = 3x - 1平行,则 k = .
3
(0,-3)
一、三、四
增大
(1.5,0)
7 已知直线 y=(2m+4)x+m-3,求:
(1)当m 为何值时,y 随x 的增大而增大?
(2)当m 为何值时,图象与y 轴的交点在x 轴下方?
(3)当m 为何值时,函数图象经过原点?
(4)当m 为何值时,这条直线平行于直线y=-x?
(1)2m+4>0,∴m>-2.
(2)m-3<0,∴m<3.
(3)m-3=0,∴m=3.
(4)2m+4=-1,∴m=- .
8 平面直角坐标系xOy 中,点P 的坐标为(m+1,m-1).
(1)试判断点P 是否在一次函数y=x-2的图象上,并 说明理由;
(2)如图,一次函数y=- x+3的图象与x 轴、y 轴分 别相交于A、B,若点P 在△AOB 的内部,求m 的取值范围.
(1)∵当x=m+1时,y=m+1-2=m-1,
∴点P (m+1,m-1)在函数 y=x-2的图象上.
(2)∵函数 y=- x+3,∴A (6,0),B (0,3).
∵点P 在△AOB 的内部,
∴0<m+1<6,0<m-1<3,m-1<- (m+1)+3.
∴1<m< .
解:
6. 如图点 P (x,y) 第一象限内一个动点,且在直线 y = - 2x + 8 上,直线与 x 轴交于点 A.
(1) 当点 P 的横坐标为 3 时,△APO 的面积为多少
(2) 设△APO 面积为 S,含 x 的解析式表示 S,并写出 x 的取值范围.
解: (1) ∵令 y = 0,则 - 2x + 8 = 0,解得 x = 4,
∴OA = 4,
∵点 P (x,y) 是第一象限内一个动点,且在直线 y = - 2x + 8 上,
∴当 x = 3 时,y = (-2)×3 + 8 = 2,
∴S△APO = ×4×2 = 4.
6. 如图点 P (x,y) 第一象限内一个动点,且在直线 y = - 2x + 8 上,直线与 x 轴交于点 A.
(2) 设△APO 面积为 S,含 x 的解析式表示 S,并写出 x 的取值范围.
(2)∵点 P (x,-2x + 8),
∴S△APO = OA×(- 2x + 8) = ×4×(-2x + 8)
= - 4x + 16 (0<x<4 ).
