2023年中考数学复习:全等三角形练习 (含答案)
文档属性
| 名称 | 2023年中考数学复习:全等三角形练习 (含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 502.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-13 08:07:45 | ||
图片预览

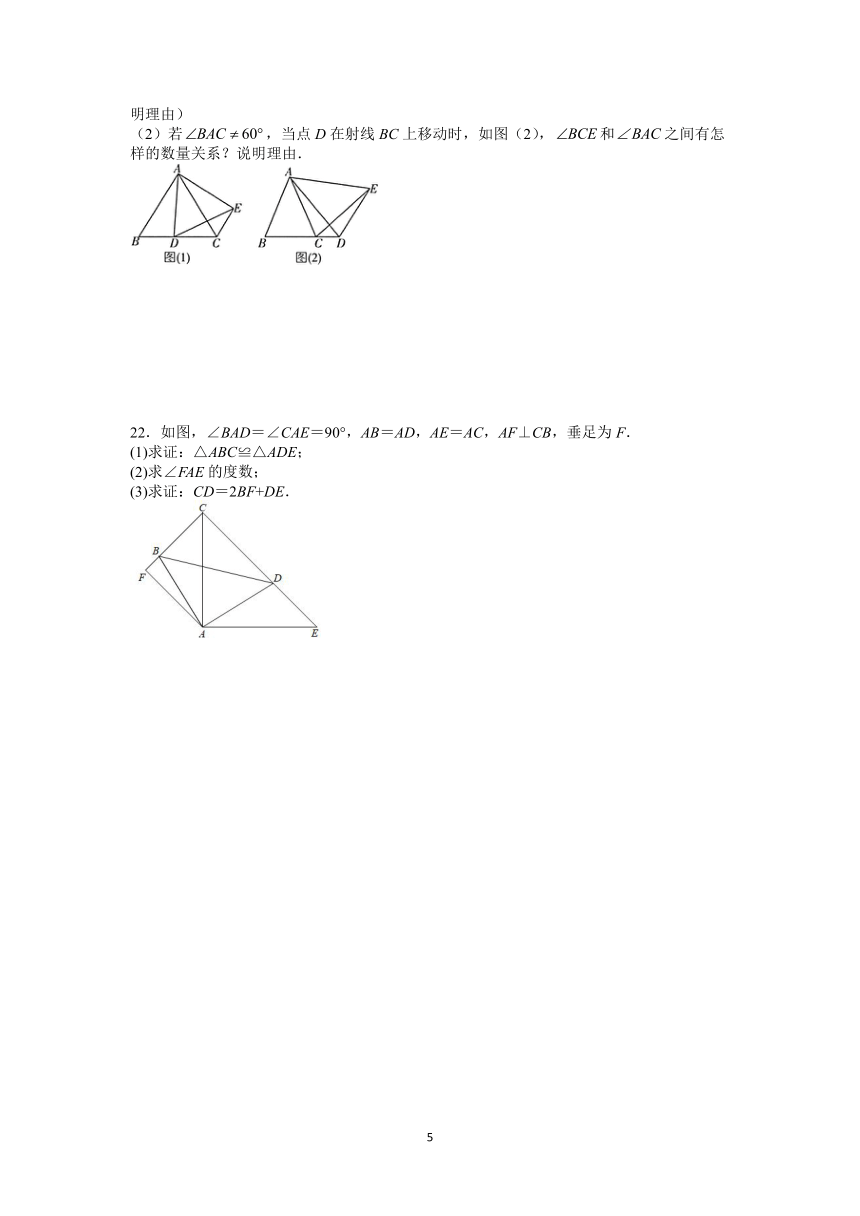
文档简介
2023年中考数学复习:全等三角形
班级:_________ 姓名:_________ 学号:__________
选择题(本大题共10小题,在每小题列出的选项中,选出符合题目的一项)
1.如图,已知△ABC≌△DCB,∠A=75°,∠DBC=40°,则∠DCB的度数为( )
A.75° B.65°
C.40° D.30°
2.如图,在Rt △ABC中,∠C=90°,AC=8m,,BD平分∠ABC,则点D到AB的距离为( )
A.2m B.3m C.4m D.6m
3.如图,小强利用全等三角形的知识测量池塘两端M、N的距离,如果△PQO≌△NMO,则只需测出其长度的线段是( )
A.PO B.PQ C.MO D.MQ
4.如图,平分,于,于,与的交点为,则图中全等三角形共有( )
A.2对 B.3对 C.4对 D.5对
5.如图,在方格纸中,以AB为一边作△ABP,使之与△ABC全等,从P1,P2,P3,P4四个点中找出符合条件的点P,则点P有( )
A.1个 B.2个 C.3个 D.4个
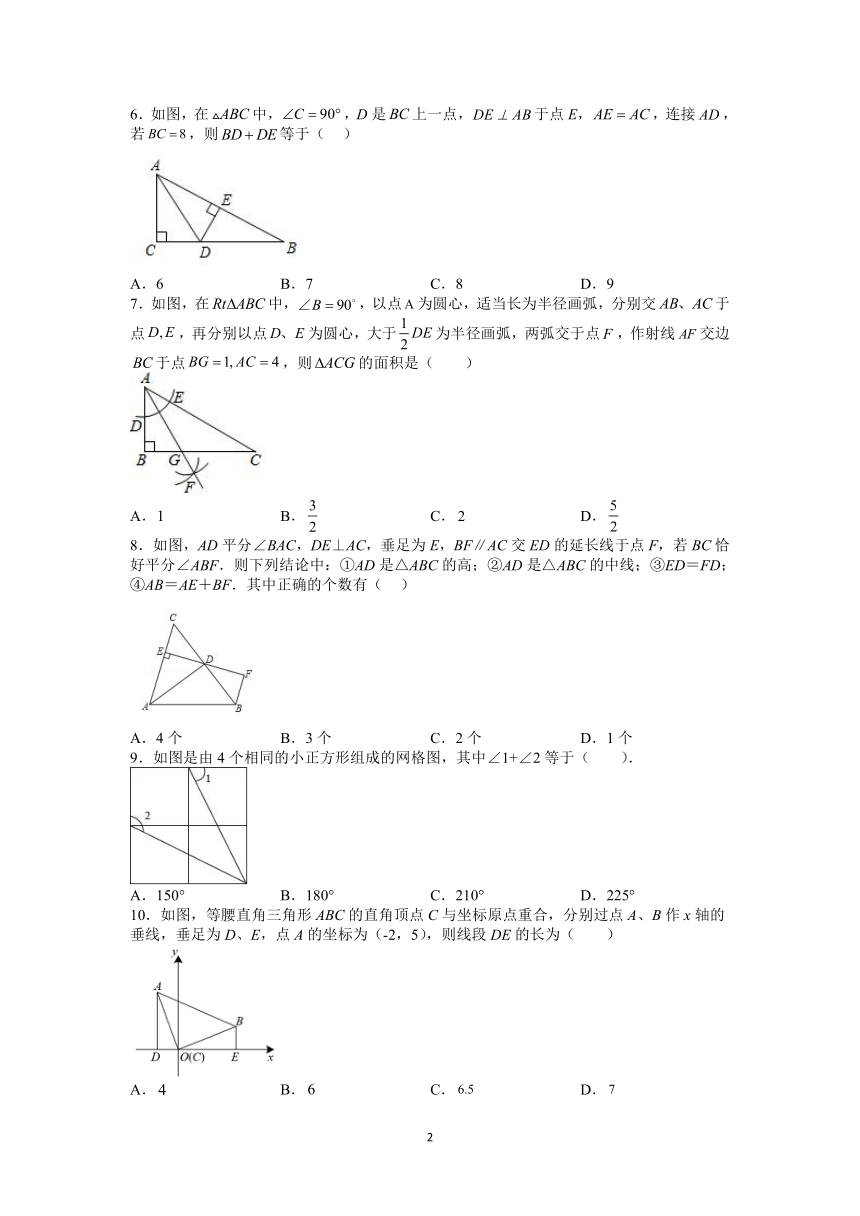
6.如图,在中,,D是上一点,于点E,,连接,若,则等于( )
A.6 B.7 C.8 D.9
7.如图,在中,,以点为圆心,适当长为半径画弧,分别交于点,再分别以点为圆心,大于为半径画弧,两弧交于点,作射线交边于点,则的面积是( )
A. B. C. D.
8.如图,AD平分∠BAC,DE⊥AC,垂足为E,BF∥AC交ED的延长线于点F,若BC恰好平分∠ABF.则下列结论中:①AD是△ABC的高;②AD是△ABC的中线;③ED=FD;④AB=AE+BF.其中正确的个数有( )
A.4个 B.3个 C.2个 D.1个
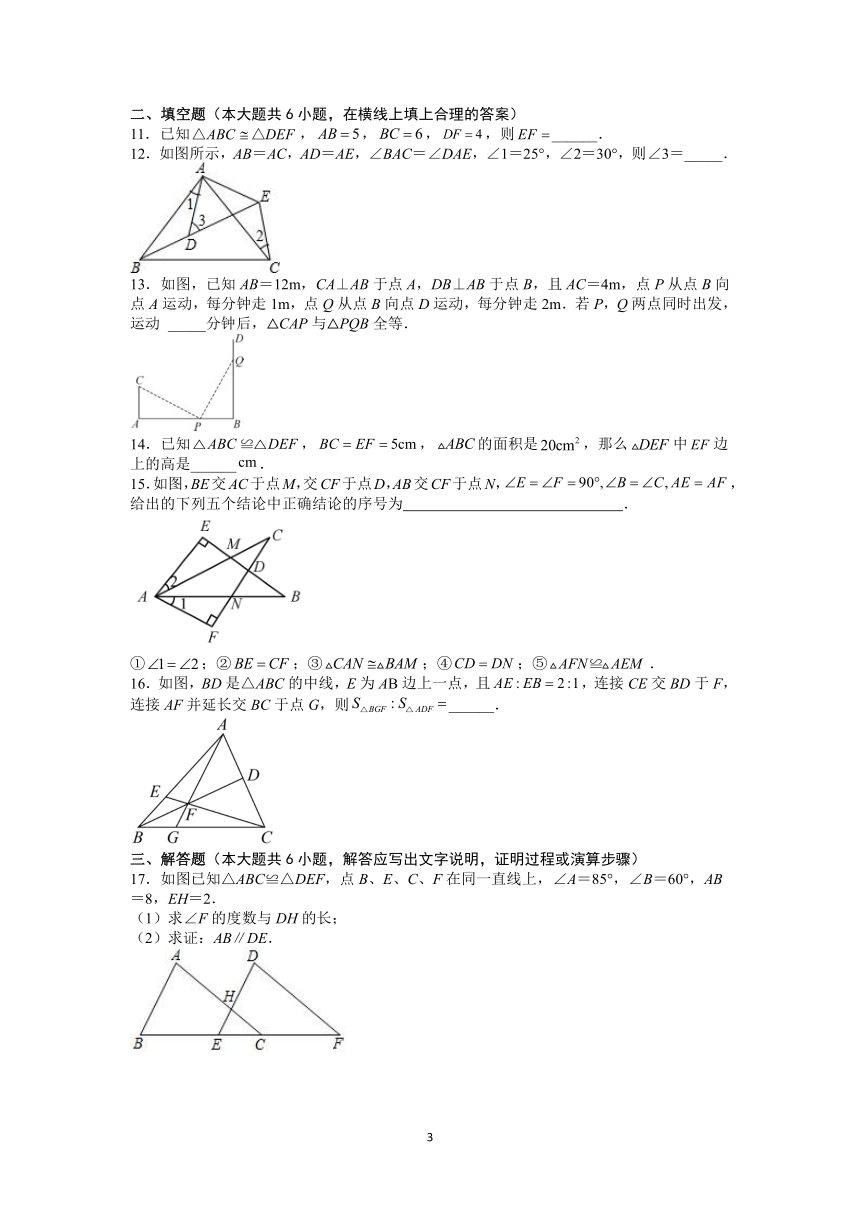
9.如图是由4个相同的小正方形组成的网格图,其中∠1+∠2等于( ).
A.150° B.180° C.210° D.225°
10.如图,等腰直角三角形ABC的直角顶点C与坐标原点重合,分别过点A、B作x轴的垂线,垂足为D、E,点A的坐标为(-2,5),则线段DE的长为( )
A. B. C. D.
二、填空题(本大题共6小题,在横线上填上合理的答案)
11.已知,,,,则______.
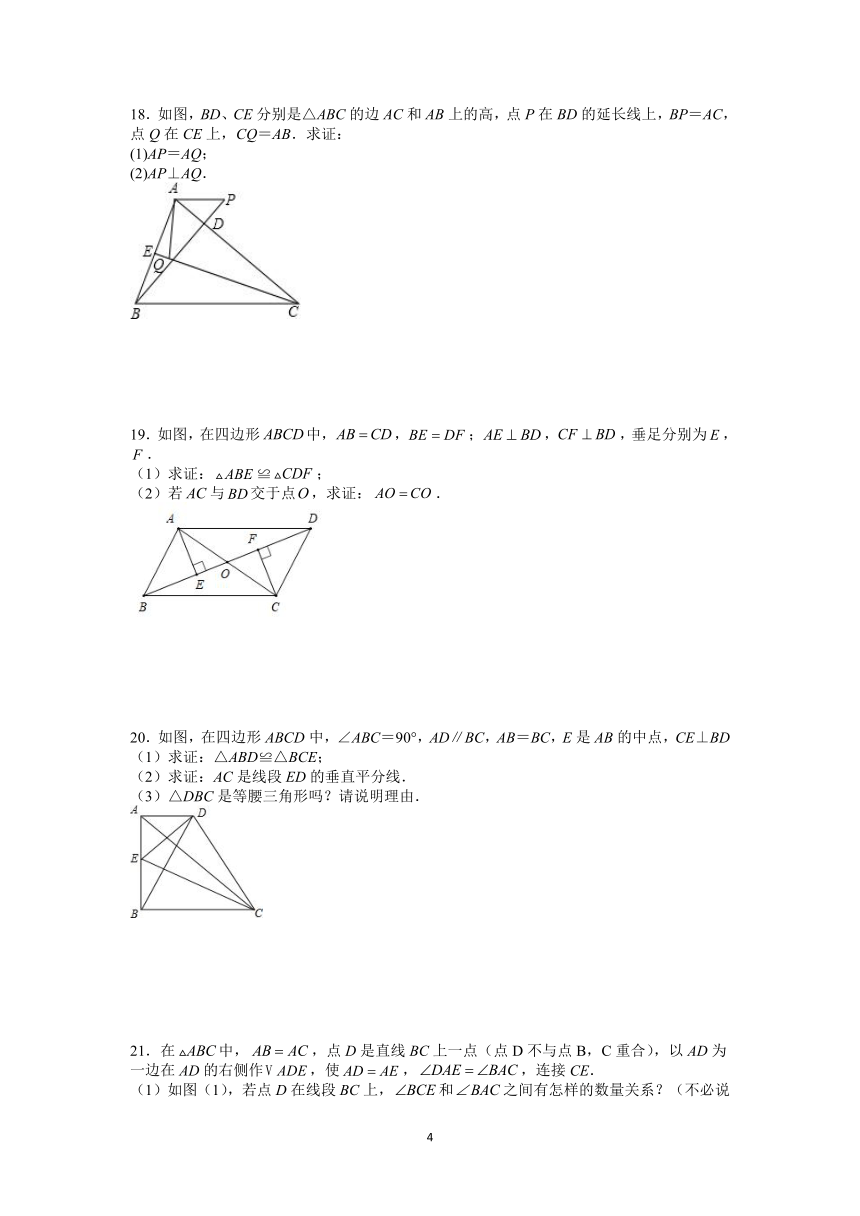
12.如图所示,AB=AC,AD=AE,∠BAC=∠DAE,∠1=25°,∠2=30°,则∠3=_____.
13.如图,已知AB=12m,CA⊥AB于点A,DB⊥AB于点B,且AC=4m,点P从点B向点A运动,每分钟走1m,点Q从点B向点D运动,每分钟走2m.若P,Q两点同时出发,运动 _____分钟后,△CAP与△PQB全等.
14.已知,,的面积是,那么中边上的高是______.
15.如图,BE交AC于点M,交CF于点D,AB交CF于点N,,给出的下列五个结论中正确结论的序号为 .
①;②;③;④;⑤.
16.如图,BD是△ABC的中线,E为AB边上一点,且,连接CE交BD于F,连接AF并延长交BC于点G,则______.
三、解答题(本大题共6小题,解答应写出文字说明,证明过程或演算步骤)
17.如图已知△ABC≌△DEF,点B、E、C、F在同一直线上,∠A=85°,∠B=60°,AB=8,EH=2.
(1)求∠F的度数与DH的长;
(2)求证:AB∥DE.
18.如图,BD、CE分别是△ABC的边AC和AB上的高,点P在BD的延长线上,BP=AC,点Q在CE上,CQ=AB.求证:
(1)AP=AQ;
(2)AP⊥AQ.
19.如图,在四边形中,,;,,垂足分别为,.
(1)求证:≌;
(2)若与交于点,求证:.
20.如图,在四边形ABCD中,∠ABC=90°,AD∥BC,AB=BC,E是AB的中点,CE⊥BD
(1)求证:△ABD≌△BCE;
(2)求证:AC是线段ED的垂直平分线.
(3)△DBC是等腰三角形吗?请说明理由.
21.在中,,点D是直线BC上一点(点D不与点B,C重合),以AD为一边在AD的右侧作,使,,连接CE.
(1)如图(1),若点D在线段BC上,和之间有怎样的数量关系?(不必说明理由)
(2)若,当点D在射线BC上移动时,如图(2),和之间有怎样的数量关系?说明理由.
22.如图,∠BAD=∠CAE=90°,AB=AD,AE=AC,AF⊥CB,垂足为F.
(1)求证:△ABC≌△ADE;
(2)求∠FAE的度数;
(3)求证:CD=2BF+DE.
答案:
1.B 2.A 3.B 4.C 5.C 6.C 7.C 8.A 9.B 10.D 11.6
12.55° 13.4 14.8 15.①;②;③;⑤ 16.
17.解:(1)在中,,,∴
∵
∴,
∴
故答案为,
(2)∵
∴
∴
18.(1)证明:∵BD⊥AC,CE⊥AB(已知),
∴∠BEC=∠BDC=90°,
∴∠ABD+∠BAC=90°,∠ACE+∠BAC=90°(直角三角形两个锐角互余),
∴∠ABD=∠ACE(等角的余角相等),
在△ABP和△QCA中,
,
∴△ABP≌△QCA(SAS),
∴AP=AQ(全等三角形对应边相等).
(2)由(1)可得∠CAQ=∠P(全等三角形对应角相等),
∵BD⊥AC(已知),
∵∠P+∠CAP=90°(直角三角形两锐角互余),
∴∠CAQ+∠CAP=90°(等量代换),即∠QAP=90°,
∴AP⊥AQ.
19.(1)证明:∵,,
∴,
∵,,
∴≌.
(2)由(1)≌,
∴,
∵,,
∴,
∵,
∴
∴.
20.解:(1)如图证明:∵∠ABC=90°,BD⊥EC,
∴∠1+∠3=90°,∠2+∠3=90°,
∴∠1=∠2,
在△BAD和△CBE中,
,
∴△BAD≌△CBE(ASA),
(2)证明:∵E是AB中点,
∴EB=EA,
∵AD=BE,
∴AE=AD,
∵AD∥BC,
∴∠7=∠ACB=45°,
∵∠6=45°,
∴∠6=∠7,
又∵AD=AE,
∴AM⊥DE,且EM=DM,
即AC是线段ED的垂直平分线;
(3)△DBC是等腰三角形(CD=BD).
理由如下:
∵由(2)得:CD=CE,由(1)得:CE=BD,
∴CD=BD.
∴△DBC是等腰三角形.
21.(1).理由如下:
,
.
,,
,
,
∴=
∵
∴;
(2).理由如下:
设AD与CE交于F点.
,.
,,
,.
,.
,,
.
22.(1)证明:∵,
∴,,
∴,
在△BAC和△DAE中,
∵,
∴;
(2)解:∵,,
∴,
由(1)知,
∴,
∵,
∴,
∴,
∴;
(3)证明:延长BF到G,使得,
∵,
∴,
在△AFB和△AFG中,
∴,
∴,
∴,,
∵,
∴,,,
∴,,
∴,
∵,
∴在△CGA和△CDA中,
,
∴,
∴,
∵,
∴.
班级:_________ 姓名:_________ 学号:__________
选择题(本大题共10小题,在每小题列出的选项中,选出符合题目的一项)
1.如图,已知△ABC≌△DCB,∠A=75°,∠DBC=40°,则∠DCB的度数为( )
A.75° B.65°
C.40° D.30°
2.如图,在Rt △ABC中,∠C=90°,AC=8m,,BD平分∠ABC,则点D到AB的距离为( )
A.2m B.3m C.4m D.6m
3.如图,小强利用全等三角形的知识测量池塘两端M、N的距离,如果△PQO≌△NMO,则只需测出其长度的线段是( )
A.PO B.PQ C.MO D.MQ
4.如图,平分,于,于,与的交点为,则图中全等三角形共有( )
A.2对 B.3对 C.4对 D.5对
5.如图,在方格纸中,以AB为一边作△ABP,使之与△ABC全等,从P1,P2,P3,P4四个点中找出符合条件的点P,则点P有( )
A.1个 B.2个 C.3个 D.4个
6.如图,在中,,D是上一点,于点E,,连接,若,则等于( )
A.6 B.7 C.8 D.9
7.如图,在中,,以点为圆心,适当长为半径画弧,分别交于点,再分别以点为圆心,大于为半径画弧,两弧交于点,作射线交边于点,则的面积是( )
A. B. C. D.
8.如图,AD平分∠BAC,DE⊥AC,垂足为E,BF∥AC交ED的延长线于点F,若BC恰好平分∠ABF.则下列结论中:①AD是△ABC的高;②AD是△ABC的中线;③ED=FD;④AB=AE+BF.其中正确的个数有( )
A.4个 B.3个 C.2个 D.1个
9.如图是由4个相同的小正方形组成的网格图,其中∠1+∠2等于( ).
A.150° B.180° C.210° D.225°
10.如图,等腰直角三角形ABC的直角顶点C与坐标原点重合,分别过点A、B作x轴的垂线,垂足为D、E,点A的坐标为(-2,5),则线段DE的长为( )
A. B. C. D.
二、填空题(本大题共6小题,在横线上填上合理的答案)
11.已知,,,,则______.
12.如图所示,AB=AC,AD=AE,∠BAC=∠DAE,∠1=25°,∠2=30°,则∠3=_____.
13.如图,已知AB=12m,CA⊥AB于点A,DB⊥AB于点B,且AC=4m,点P从点B向点A运动,每分钟走1m,点Q从点B向点D运动,每分钟走2m.若P,Q两点同时出发,运动 _____分钟后,△CAP与△PQB全等.
14.已知,,的面积是,那么中边上的高是______.
15.如图,BE交AC于点M,交CF于点D,AB交CF于点N,,给出的下列五个结论中正确结论的序号为 .
①;②;③;④;⑤.
16.如图,BD是△ABC的中线,E为AB边上一点,且,连接CE交BD于F,连接AF并延长交BC于点G,则______.
三、解答题(本大题共6小题,解答应写出文字说明,证明过程或演算步骤)
17.如图已知△ABC≌△DEF,点B、E、C、F在同一直线上,∠A=85°,∠B=60°,AB=8,EH=2.
(1)求∠F的度数与DH的长;
(2)求证:AB∥DE.
18.如图,BD、CE分别是△ABC的边AC和AB上的高,点P在BD的延长线上,BP=AC,点Q在CE上,CQ=AB.求证:
(1)AP=AQ;
(2)AP⊥AQ.
19.如图,在四边形中,,;,,垂足分别为,.
(1)求证:≌;
(2)若与交于点,求证:.
20.如图,在四边形ABCD中,∠ABC=90°,AD∥BC,AB=BC,E是AB的中点,CE⊥BD
(1)求证:△ABD≌△BCE;
(2)求证:AC是线段ED的垂直平分线.
(3)△DBC是等腰三角形吗?请说明理由.
21.在中,,点D是直线BC上一点(点D不与点B,C重合),以AD为一边在AD的右侧作,使,,连接CE.
(1)如图(1),若点D在线段BC上,和之间有怎样的数量关系?(不必说明理由)
(2)若,当点D在射线BC上移动时,如图(2),和之间有怎样的数量关系?说明理由.
22.如图,∠BAD=∠CAE=90°,AB=AD,AE=AC,AF⊥CB,垂足为F.
(1)求证:△ABC≌△ADE;
(2)求∠FAE的度数;
(3)求证:CD=2BF+DE.
答案:
1.B 2.A 3.B 4.C 5.C 6.C 7.C 8.A 9.B 10.D 11.6
12.55° 13.4 14.8 15.①;②;③;⑤ 16.
17.解:(1)在中,,,∴
∵
∴,
∴
故答案为,
(2)∵
∴
∴
18.(1)证明:∵BD⊥AC,CE⊥AB(已知),
∴∠BEC=∠BDC=90°,
∴∠ABD+∠BAC=90°,∠ACE+∠BAC=90°(直角三角形两个锐角互余),
∴∠ABD=∠ACE(等角的余角相等),
在△ABP和△QCA中,
,
∴△ABP≌△QCA(SAS),
∴AP=AQ(全等三角形对应边相等).
(2)由(1)可得∠CAQ=∠P(全等三角形对应角相等),
∵BD⊥AC(已知),
∵∠P+∠CAP=90°(直角三角形两锐角互余),
∴∠CAQ+∠CAP=90°(等量代换),即∠QAP=90°,
∴AP⊥AQ.
19.(1)证明:∵,,
∴,
∵,,
∴≌.
(2)由(1)≌,
∴,
∵,,
∴,
∵,
∴
∴.
20.解:(1)如图证明:∵∠ABC=90°,BD⊥EC,
∴∠1+∠3=90°,∠2+∠3=90°,
∴∠1=∠2,
在△BAD和△CBE中,
,
∴△BAD≌△CBE(ASA),
(2)证明:∵E是AB中点,
∴EB=EA,
∵AD=BE,
∴AE=AD,
∵AD∥BC,
∴∠7=∠ACB=45°,
∵∠6=45°,
∴∠6=∠7,
又∵AD=AE,
∴AM⊥DE,且EM=DM,
即AC是线段ED的垂直平分线;
(3)△DBC是等腰三角形(CD=BD).
理由如下:
∵由(2)得:CD=CE,由(1)得:CE=BD,
∴CD=BD.
∴△DBC是等腰三角形.
21.(1).理由如下:
,
.
,,
,
,
∴=
∵
∴;
(2).理由如下:
设AD与CE交于F点.
,.
,,
,.
,.
,,
.
22.(1)证明:∵,
∴,,
∴,
在△BAC和△DAE中,
∵,
∴;
(2)解:∵,,
∴,
由(1)知,
∴,
∵,
∴,
∴,
∴;
(3)证明:延长BF到G,使得,
∵,
∴,
在△AFB和△AFG中,
∴,
∴,
∴,,
∵,
∴,,,
∴,,
∴,
∵,
∴在△CGA和△CDA中,
,
∴,
∴,
∵,
∴.
同课章节目录
