第六单元正比例和反比例拔尖特训卷(单元测试)-小学数学六年级下册苏教版(含答案)
文档属性
| 名称 | 第六单元正比例和反比例拔尖特训卷(单元测试)-小学数学六年级下册苏教版(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-13 07:31:06 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第六单元正比例和反比例拔尖特训卷(单元测试)-小学数学六年级下册苏教版
一、选择题
1.下面各题中,( )中的两种量不成比例。
A.正方体底面积一定,它的棱长与体积
B.三角形面积一定,它的底和高
C.圆柱的高一定,圆柱的侧面积和底面周长
2.已知2x=y-4(y>4),那么x和y( )。
A.成正比例 B.成反比例 C.不成比例
3.下列说法正确的有( )。
(1)60名同学参加团体操表演,每排的人数和排数成反比例。
(2)王奶奶把5000元存入银行2年,年利率是3.75%,她到期时可以取回5375元。
(3)2019年的第一季度是91天。
(4)半圆的周长是它所在圆周长的一半。
A.1个 B.2个 C.3个
4.小丽从家步行到学校已走的路程和还剩的路程( )。
A.成正比例 B.不成比例 C.成反比例
5.如果A×2=B÷3,那么A∶B=( )。
A.2∶3 B.3∶2 C.1∶6
6.下面两个量成正比例关系的是( )。
A.正方体体积和棱长 B.小明的身高和年龄 C.汽车耗油量和行程
二、填空题
7.如果5a=3b(a,b均不为0),那么。
8.如果5a=9b,那么a和b成( )比例;如果=,那么和y成( )比例;如果m∶3=10∶n,那么m和n成( )比例。
9.运一批砖,每次运的块数与运砖的次数成( )比例;比的后项一定,比的前项与比值成( )比例。
10.如果用字母和y表示两种相关联的量,用k表示它们的比值,正比例关系可以表示为( );如果用字母x和y表示两种相关联的量,用k表示它们的积,反比例关系可以表示为( )。
11.加工一批零件的时间一定,加工每个零件所花的时间和零件个数成( )比例;加工一个零件的时间一定,加工零件的总个数和加工零件的时间成( )比例。
12.小红在操场上插了4根长短不同的竹竿,在同一时间里测量竹竿长和相应的影长如下表:
竹竿长/米 1 1.2 1.6 2
影长/米 0.75 0.9 1.2 1.5
这时,小红测量出校园中旗杆的影长是6米,可推算出旗杆的实际高度是( )米。
三、判断题
13.一条路,修了的米数和未修的米数成反比例。( )
14.xy是两种相关联的量,且x-y=0(x与y都不为零),那么x与y不成比例。( )
15.(a不等于0),a和b不成比例。( )
16.在1∶20000的地图上,图上距离和实际距离成正比例。( )
17.某食堂12天烧煤15吨,照这样计算,100吨煤可以烧多少天?解答时设100吨可以烧X天.列式为12:15 =100:X ( )
四、计算题
18.求未知数。
25%x+20%x=90 x∶=12∶ x-40%x=
五、解答题
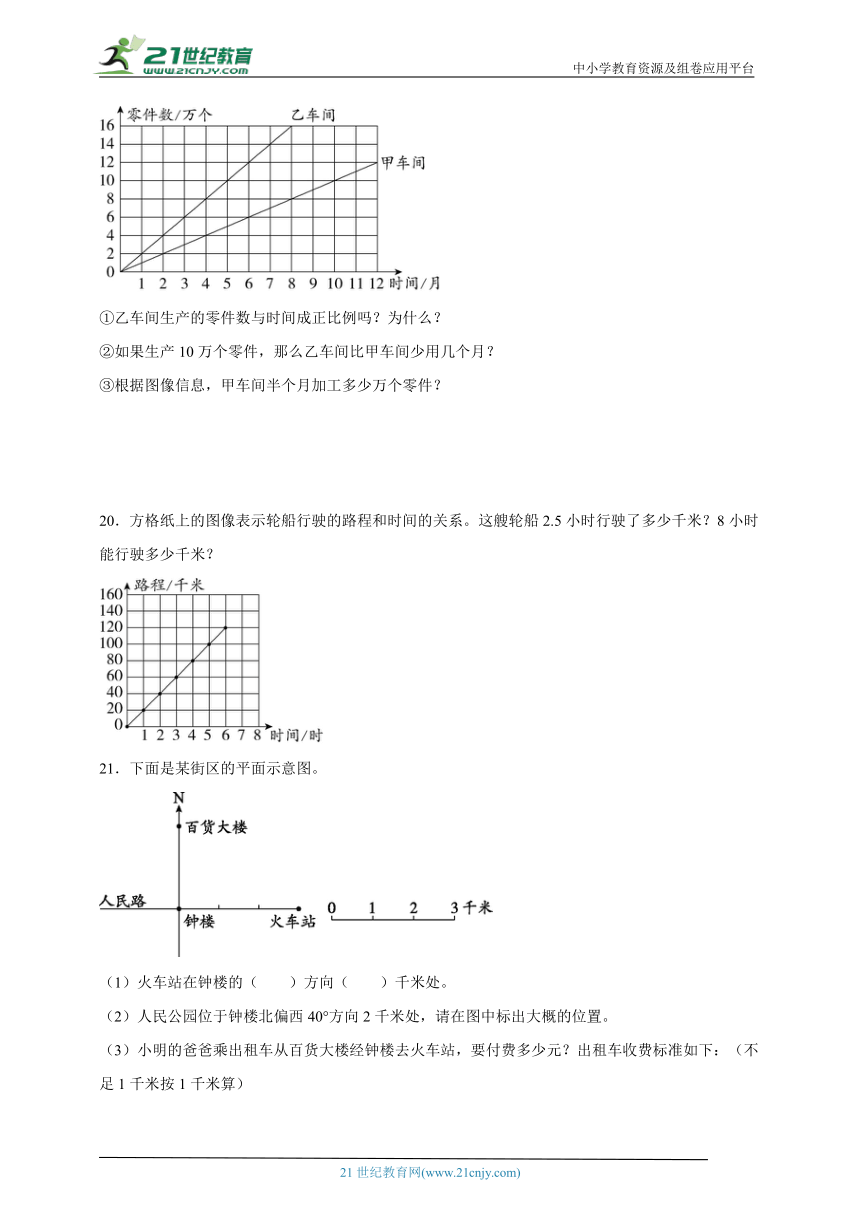
19.如图表示某工厂中甲、乙两个车间加工的零件数与时间的关系。
①乙车间生产的零件数与时间成正比例吗?为什么?
②如果生产10万个零件,那么乙车间比甲车间少用几个月?
③根据图像信息,甲车间半个月加工多少万个零件?
20.方格纸上的图像表示轮船行驶的路程和时间的关系。这艘轮船2.5小时行驶了多少千米?8小时能行驶多少千米?
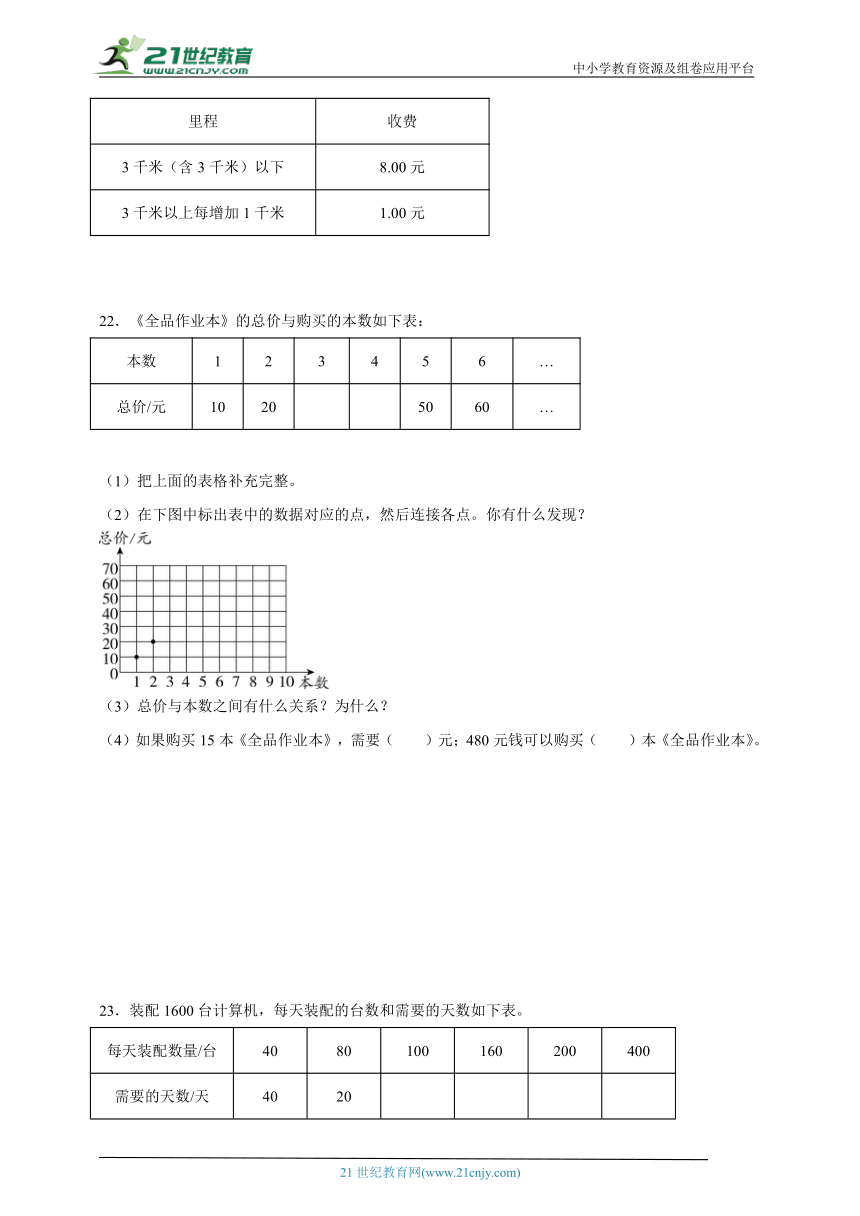
21.下面是某街区的平面示意图。
(1)火车站在钟楼的( )方向( )千米处。
(2)人民公园位于钟楼北偏西40°方向2千米处,请在图中标出大概的位置。
(3)小明的爸爸乘出租车从百货大楼经钟楼去火车站,要付费多少元?出租车收费标准如下:(不足1千米按1千米算)
里程 收费
3千米(含3千米)以下 8.00元
3千米以上每增加1千米 1.00元
22.《全品作业本》的总价与购买的本数如下表:
本数 1 2 3 4 5 6 …
总价/元 10 20 50 60 …
(1)把上面的表格补充完整。
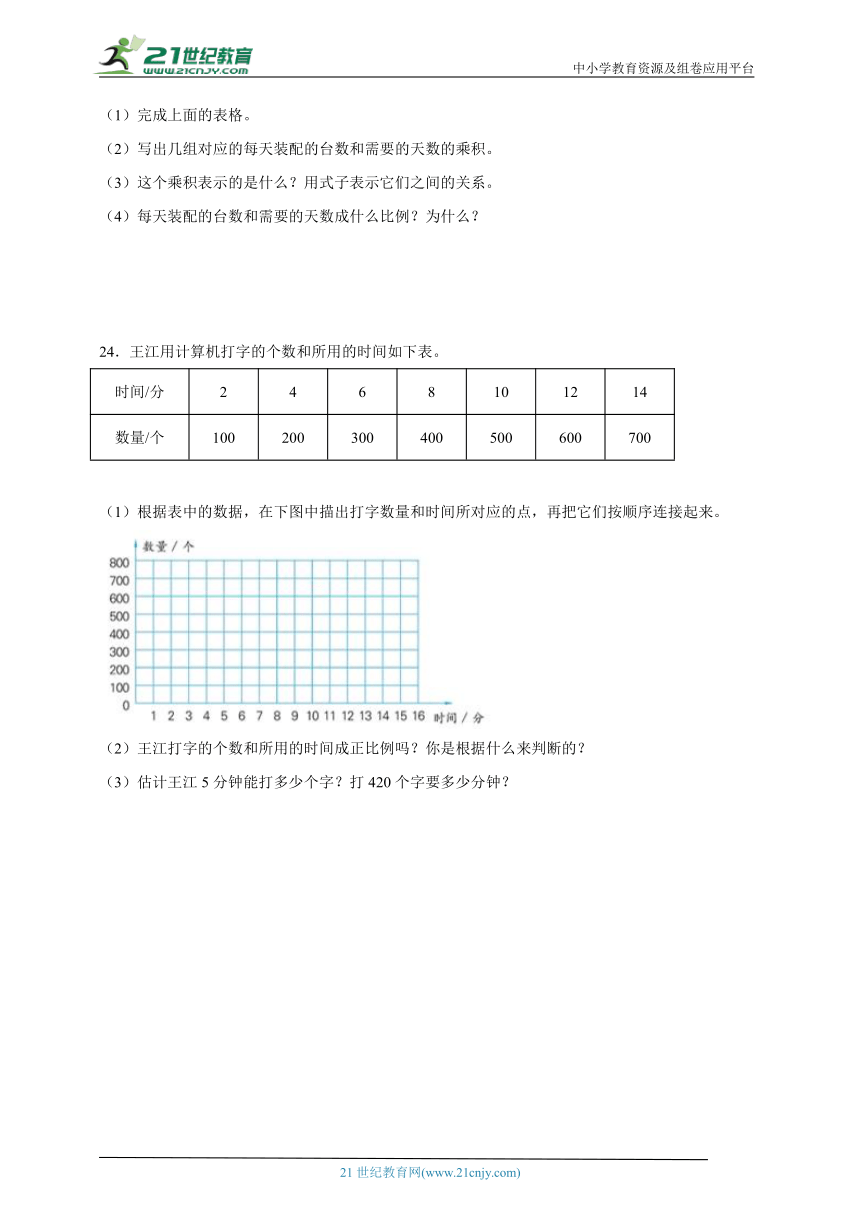
(2)在下图中标出表中的数据对应的点,然后连接各点。你有什么发现?
(3)总价与本数之间有什么关系?为什么?
(4)如果购买15本《全品作业本》,需要( )元;480元钱可以购买( )本《全品作业本》。
23.装配1600台计算机,每天装配的台数和需要的天数如下表。
每天装配数量/台 40 80 100 160 200 400
需要的天数/天 40 20
(1)完成上面的表格。
(2)写出几组对应的每天装配的台数和需要的天数的乘积。
(3)这个乘积表示的是什么?用式子表示它们之间的关系。
(4)每天装配的台数和需要的天数成什么比例?为什么?
24.王江用计算机打字的个数和所用的时间如下表。
时间/分 2 4 6 8 10 12 14
数量/个 100 200 300 400 500 600 700
(1)根据表中的数据,在下图中描出打字数量和时间所对应的点,再把它们按顺序连接起来。
(2)王江打字的个数和所用的时间成正比例吗?你是根据什么来判断的?
(3)估计王江5分钟能打多少个字?打420个字要多少分钟?
参考答案:
1.A
【分析】判断两种相关联的量成不成比例,成什么比例,就看这两种量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,就成反比例,如果是其它的量一定或乘积、比值不一定,就不成比例。
【详解】A.正方体底面积一定,则正方体的棱长一定,体积也一定,所以正方体底面积一定,它的棱长与体积不成比例;
B.三角形的底×高=三角形的面积(一定),即底和高的乘积一定,所以三角形面积一定,它的底和高成反比例;
C.圆柱的侧面积÷底面周长=圆柱的高(一定),即圆柱的侧面积和底面周长的比值一定,所以圆柱的高一定,圆柱的侧面积和底面周长成正比例。
故答案为:A
【点睛】此题属于根据正、反比例的意义,辨识两种相关联的量成不成比例,成什么比例,就看这两种量是否都是变量,且对应的比值一定,或是对应的乘积一定,再做出判断。
2.C
【分析】判断两种相关联的量成不成比例,成什么比例,就看这两种量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,就成反比例,如果是其它的量一定或乘积、比值不一定,就不成比例。
【详解】由2x=y-4(y>4)可知:y-2x=4,乘积与比值均不一定,所以x和y不成比例。
故答案为:C
【点睛】此题属于根据正、反比例的意义,辨识两种相关联的量成不成比例,成什么比例,就看这两种量是否都是变量,且对应的比值一定,或是对应的乘积一定,再做出判断。
3.B
【分析】(1)判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例;
(2)本息=本金+利息,利息=本金×利率×时间,代入数据计算即可;
(3)2019年是平年,2月有28天,1、3月有31天,由此求出第一季度天数即可;
(4)半圆的周长=圆周长的一半+直径;据此逐项判断即可。
【详解】(1)每排的人数×排数=总人数(60名同学),也就是每排的人数与排数的乘积一定所以60名同学参加团体操表演,每排的人数和排数成反比例;原说法正确。
(2)5000+5000×3.75%×2
=5000+375
=5375(元)
到期时王奶奶可以取回5375元;原说法正确。
(3)2019年是平年,2月有28天,第一季度共31+28+31=90天;原说法错误。
(4)半圆的周长是它所在圆周长的一半+直径;原说法错误。
综上可知:正确说法有2个。
故答案为:B
【点睛】本题考查知识点较多,解题时注意半圆的周长与圆周长的关系。
4.B
【分析】判断小丽步行已走的路程与剩下的路程成不成比例,成什么比例,就看这两种量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,就成反比例,如果是其它的量一定或乘积、比值不一定,就不成比例.据此进行判断后再选择。
【详解】因为步行的路程+剩下的路程=从家到学校的路程(一定),
是对应的“和”一定,不是“乘积或比值”一定,
所以小丽步行已走的路程与剩下的路程不成比例。
故答案为:B。
【点睛】此题属于根据正、反比例的意义,辨识两种相关联的量成不成比例,成什么比例,就看这两种量是对应的比值一定,还是对应的乘积一定,还是对应的其它量一定,再做出判断。
5.C
【分析】把除法转化成乘法后,根据比例的基本性质写出比例,然后把后面的比化成最简整数比即可做出选择。
【详解】A×2=B÷3,则A×2=B×,那么A∶B=∶2=1∶6。
故答案为:C
【点睛】灵活运用比例的基本性质。
6.C
【分析】两个量成正比例关系,即一个量变化,另一个量也随之变化,但它们的比值是恒定的。
【详解】A.正方体的体积=棱长×棱长×棱长,它与棱长的比值并不是常数,所以该选项错误;
B.小明的身高会随着年龄变化而变化,但比值不是常数,所以选项错误;
C.汽车的耗油量=每公里耗油量×行程,它们的比值是恒定的,所以选项正确。
故答案选择C。
【点睛】本题考查的是两个量正比例关系的定义,准确判定两个量的比值否恒定是解题的关键。
7.
【分析】根据等式的性质,两边同时除以相同的数,等式仍然成立。
【详解】5a=3b
5a÷3a=3b÷3a
=
=
=
【点睛】熟练掌握等式的性质和比例的基本性质才是解此题的核心。
8. 正 正 反
【分析】判断两个相关联的量之间成什么比例,就看这两个量对应是的比值一定,还是对应的乘积一定;如果比值一定,就成正比例;如果乘积一定,则成反比例。
【详解】(1)根据比例的基本性质:两个内项的乘积等于两个外项的乘积。5a=9b可转变为比例的形式:a∶b=9∶5,即a÷b=,即a和b的比值一定,成正比例;
(2)=,进行交叉相乘,得:11x=7y,再根据比例的基本性质可转变为比例的形式:x∶y=7∶11,即x÷y=,即x和y的比值一定,成正比例;
(3)m∶3=10∶n, 根据比例的基本性质可转变为乘积的形式:mn=30,即m和n的乘积一定,成反比例。
故答案为:(1)正;(2)正;(3)反。
【点睛】熟练掌握的正比例和反比例的概念是解题的关键。
9. 反 正
【分析】判断两个相关联的量之间成什么比例,就看这两个量对应是的比值一定,还是对应的乘积一定;如果比值一定,就成正比例;如果乘积一定,则成反比例。
【详解】(1)每次运的块数×运砖次数=这批砖的总块数(一定),乘积一定,成反比例;
(2)比的前项÷比值=比的后项(一定),比值一定,成正比例。
故答案:(1)反;(2)正。
【点睛】熟练掌握的正比例和反比例的概念是解题的关键。
10. =k(一定)(x≠0) xy=k(一定)
【分析】正比例:相关联的两个量,比值一定。反比例:相关联的两个量,乘积一定。
【详解】如果用字母x和y表示两种相关联的量,用k表示它们的比值,正比例关系可以表示为( =k(一定)(x≠0) );如果用字母x和y表示两种相关联的量,用k表示它们的积,反比例关系可以表示为( xy=k(一定) )。
【点睛】熟练掌握的正比例和反比例的概念是解题的关键。
11. 反 正
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
【详解】(1)加工零件时间(一定)=每个零件加工时间×零件个数,乘积一定,成反比例;
(2)加工一个零件的时间(一定)=加工零件总个数÷加工零件时间,比值一定,成正比例。
【点睛】此题主要考查正、反比例的辨识,就看这两个量是对应的比值一定,还是对应的乘积一定,再做判断。
12.8
【分析】首先判断竹竿长与影长成什么比例,再通过比例求出旗杆的影长是6米时,算出旗杆的实际高度。判断两个相关联的量之间成什么比例,就看这两个量对应是的比值一定,还是对应的乘积一定;如果比值一定,就成正比例;如果乘积一定,则成反比例。
【详解】(1)1÷0.75=1÷=1×=;(2)1.2÷0.9=12÷9==;(4)1.6÷1.2=16÷12==;(4)2÷1.5=20÷15==;通过上述四个式子可以得知:竹竿长÷影长=(一定),竹竿长和影长的比值一定,成反比例。
当小红测量出校园中旗杆的影长是6米,即竹竿长∶影长=旗杆实际高度∶旗杆影长,设旗杆实际高度为X米。
可得:1∶0.75=X∶6
解:0.75X=6
X=6÷0.75
X=8
所以旗杆的实际高度是8米。
【点睛】熟练掌握的正、反比例的概念和比例的基本性质是解题的关键。
13.×
【分析】判断修了的米数和未修的米数是否成反比例,就看这两种量是否是对应的乘积一定,如果是乘积一定,就成反比例,如果不是乘积一定,就不成反比例。据此进行判断。
【详解】修了的米数+未修的米数=一条路的总米数(一定),是和一定,不是乘积一定,所以修了的米数和未修的米数不成反比例。
【点睛】此题属于辨识两种相关联的量是否成反比例,就看这两种量是否是对应的乘积一定,再做出判断。
14.×
【分析】判断两个相关联的量之间成什么比例,就看这两个量对应是的比值一定,还是对应的乘积一定;如果比值一定,就成正比例;如果乘积一定,则成反比例;无上述两种情况,则不成比例。
【详解】xy是两种相关联的量,且x-y=0(x与y都不为零),即x=y,所以x÷y=x∶y=1,即x和y的比值一定,成正比例。
故答案:×。
【点睛】熟练掌握的正、反比例的概念以及等式的变形是解题的关键。
15.×
【分析】两种相关联的量都是变量,且对应的乘积一定,就成反比例;对应的比值一定,就成正比例;否则就不成比例。
【详解】(a不等于0),5ab=8,ab=,即乘积一定,成反比例。
故答案为:×
【点睛】考查了正比例、反比例的意义和辨别,基础题。
16.√
【分析】比例尺=,比值一定,成正比例关系,据此解答。
【详解】根据分析可得,在1∶20000的地图上,图上距离和实际距离成正比例,原题说法正确。
故答案为:√
【点睛】在同一幅地图上,比例尺是定值,图上距离和实际距离成正比例关系,积一定是反比例关系。
17.√
【详解】题目中每天烧煤的吨数一定,烧煤的天数和烧煤的总吨数成正比例,由此可以找到两组对应数值:12和15,100和x,所以列出的算式是在正确的.
18.(1)x=200;(2)x=15;(3)x=1。
【分析】此题为解方程和解比例的题型,需注意解方程的步骤。解比例得按照比例的基本性质,两内项乘积等于两外项乘积。
【详解】(1)25%x+20%x=90
解:0.45x=90
x=90÷0.45
x=200;
(2)x∶=12∶
解:x=×12
x=3
x=3÷
x=15;
(3)x-40%x=
解:0.6x=0.6
x=0.6÷0.6
x=1。
【点睛】熟练掌握解方程的步骤和比例的基本性质并细心计算是解此题的关键。
19.①成正比例;因为生产的零件数与时间的比值一定
②5个
③0.5万个
【分析】(1)判断生产的零件数与时间是否成正比例,就看这两种量是否是对应的比值一定,如果是比值一定,就成正比例,如果不是比值一定或比值不一定,就不成正比例;
(2)先分别求出时间,再比较即可;
(3)由图意可知,2个月生产2万个零件,即可求出半个月加工多少个零件。
【详解】(1)由图意可知,工效是一定的,工效=工作总量÷工作时间,所以乙车间生产的零件数与时间成正比例;
(2)乙生产10万个零件需要:10÷2=5(个)
甲生产10万个零件需要:10÷(2÷2)=10(个)
10-5=5(个)
答:如果生产10万个零件,那么乙车间比甲车间少用5个月。
(3)2÷2÷2=0.5(万个)
答:甲车间半个月加工0.5万个零件。
【点睛】本题考查了比例的有关知识,解题的关键是从折线统计图中得到进一步解题的相关信息。
20.50千米;160千米
【分析】船的速度为20÷1=20(千米/时),根据路程=速度×时间,即可求出本题答案。
【详解】20÷1×2.5
=20×2.5
=50(千米)
20÷1×8
=20×8
=160(千米)
答:这艘轮船2.5小时行驶了50千米,8小时能行驶160千米。
【点睛】掌握路程=速度×时间,是解决问题的关键。
21.(1)正东;3
(2)
(3)10元
【分析】(1)、(2)东北方向也叫作北偏东,西北方向也叫作北偏西,西南方向叫作南偏西,东南方向叫作南偏东,再结合平面图即可得到具体位置。
(3)量得百货大楼到钟楼的图上距离是2厘米,线段比例尺已知,所以百货大楼到钟楼的实际距离为:2×1=2(千米),火车站离钟楼的实际距离为:3×1=3(千米),所以总距离为3+2=5(千米),因为3千米(含3千米)以下,收费8元,所以有5-3=2(千米)是收费1元的,即可求出总的付费钱数。
【详解】(1)火车站在钟楼的正东方向3千米处。
(2)根据线段比例尺结合方向位置的描述可以画出来。
(3)量得百货大楼到钟楼的图上距离是2厘米。
1×2=2(千米)
2+3=5(千米)
(5-3)×1+8
=2×1+8
=2+8
=10(元)
答:小明的爸爸乘出租车从百货大楼经钟楼去火车站,要付费10元。
【点睛】掌握线段比例尺的定义是本题的解题关键。
22.(1)30;40
(2)
是一条过(0,0)点的直线。(发现合理即可)
(3)总价和本数成正比例关系,因为总价和本数是相关联的量,并且=单价(一定)。
(4)150;48
【分析】(1)因为10÷1=10,20÷2=10,50÷5=10,60÷6=10,所以根据=单价,可知单价为10元,即可求出当本数为3本、4本时候的总价。
(2)将描出的点顺次连接,得到的是一条过(0,0)点的直线。
(3)=单价,如果两种相关联的量,它们的比值是一定的,则这两种量是成正比例的量,它们的关系叫作正比例关系。
(4)根据总价=单价×本数,进行求解。
【详解】(1)因为=单价,且单价为10元,所以30÷3=10,40÷4=10,所以当本数为3本、4本的时候总价为30元、40元。
(2)通过描点连线得到的是一条过原点的直线。
(3)因为=单价,且单价一定,根据正比例关系的定义,所以两者是正比例关系。
(4)因为单价为10元,所以买15本需要15×10=150(元);用480元可以买480÷10=48(本)。
【点睛】此题考查了正比例关系的定义和总价=单价×本数的应用。
23.(1)
每天装配数量/台 40 80 100 160 200 400
需要的天数/天 40 20 16 10 8 4
(2)40×40=1600(台);80×20=1600(台);100×16=1600(台)等;
(3)这个乘积表示的是需要装配的计算机的台数,计算机的台数=每天装配的台数×需要的天数;
(4)成反比例,因为每天装配的台数×需要的天数=计算机的台数,乘积一定。
【分析】(1)利用总数量1600除以每天装配的数量即可求出对应的天数,完成表格;
(2)(3)根据题意写出几组每天的台数和需要的天数的乘积,计算出答案,然后结合表格写出乘积表示什么,表示出这个关系;
(4)仔细观察,看(3)中的乘积是不是定值,进而判断比例关系。
【详解】(1)40×40=1600(台);1600÷80=20(天);1600÷100=16(天);1600÷160=10(天);1600÷200=8(天);1600÷400=4(天)
每天装配数量/台 40 80 100 160 200 400
需要的天数/天 40 20 16 10 8 4
(2)40×40=1600(台);80×20=1600(台);100×16=1600(台)等;
(3)这个乘积表示的是需要装配的计算机的台数,计算机的台数=每天装配的台数×需要的天数;
(4)成反比例。因为每天装配的台数×需要的天数=计算机的台数,乘积一定。
【点睛】本题考查了正反比例的知识,清楚正反比例的意义是解题的关键。
24.(1)
(2)成正比例;
依据:打字的个数和所用时间是两个相关联的量,打字的个数随着所用时间的变化而变化,即打字的个数与所用时间的比值一定,所以打字的个数和所用时间成正比例。
(3)250个;8.4分钟
【分析】(1)根据横轴表示时间,纵轴表示打字个数描点,再连线即可;
(2)观察可知打字数量随时间的变化而变化,而每分钟打字个数不变,据此解答;
(3)先求出每分钟打字的个数,再根据乘除法的意义可完成解答。
【详解】(1)
(2)成正比例,依据:打字的个数和所用时间是两个相关联的量,打字的个数随着所用时间的变化而变化,即打字的个数与所用时间的比值一定,所以打字的个数和所用时间成正比例。
(3)(100÷2)×5
=50×5
=250(个)
450÷(100÷2)
=750÷50
=8.4(分钟)
答:王江5分钟能打250个字,打420个字要8.4分钟。
【点睛】本题是关于正反比例的题目,掌握正反比例的意义是关键。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第六单元正比例和反比例拔尖特训卷(单元测试)-小学数学六年级下册苏教版
一、选择题
1.下面各题中,( )中的两种量不成比例。
A.正方体底面积一定,它的棱长与体积
B.三角形面积一定,它的底和高
C.圆柱的高一定,圆柱的侧面积和底面周长
2.已知2x=y-4(y>4),那么x和y( )。
A.成正比例 B.成反比例 C.不成比例
3.下列说法正确的有( )。
(1)60名同学参加团体操表演,每排的人数和排数成反比例。
(2)王奶奶把5000元存入银行2年,年利率是3.75%,她到期时可以取回5375元。
(3)2019年的第一季度是91天。
(4)半圆的周长是它所在圆周长的一半。
A.1个 B.2个 C.3个
4.小丽从家步行到学校已走的路程和还剩的路程( )。
A.成正比例 B.不成比例 C.成反比例
5.如果A×2=B÷3,那么A∶B=( )。
A.2∶3 B.3∶2 C.1∶6
6.下面两个量成正比例关系的是( )。
A.正方体体积和棱长 B.小明的身高和年龄 C.汽车耗油量和行程
二、填空题
7.如果5a=3b(a,b均不为0),那么。
8.如果5a=9b,那么a和b成( )比例;如果=,那么和y成( )比例;如果m∶3=10∶n,那么m和n成( )比例。
9.运一批砖,每次运的块数与运砖的次数成( )比例;比的后项一定,比的前项与比值成( )比例。
10.如果用字母和y表示两种相关联的量,用k表示它们的比值,正比例关系可以表示为( );如果用字母x和y表示两种相关联的量,用k表示它们的积,反比例关系可以表示为( )。
11.加工一批零件的时间一定,加工每个零件所花的时间和零件个数成( )比例;加工一个零件的时间一定,加工零件的总个数和加工零件的时间成( )比例。
12.小红在操场上插了4根长短不同的竹竿,在同一时间里测量竹竿长和相应的影长如下表:
竹竿长/米 1 1.2 1.6 2
影长/米 0.75 0.9 1.2 1.5
这时,小红测量出校园中旗杆的影长是6米,可推算出旗杆的实际高度是( )米。
三、判断题
13.一条路,修了的米数和未修的米数成反比例。( )
14.xy是两种相关联的量,且x-y=0(x与y都不为零),那么x与y不成比例。( )
15.(a不等于0),a和b不成比例。( )
16.在1∶20000的地图上,图上距离和实际距离成正比例。( )
17.某食堂12天烧煤15吨,照这样计算,100吨煤可以烧多少天?解答时设100吨可以烧X天.列式为12:15 =100:X ( )
四、计算题
18.求未知数。
25%x+20%x=90 x∶=12∶ x-40%x=
五、解答题
19.如图表示某工厂中甲、乙两个车间加工的零件数与时间的关系。
①乙车间生产的零件数与时间成正比例吗?为什么?
②如果生产10万个零件,那么乙车间比甲车间少用几个月?
③根据图像信息,甲车间半个月加工多少万个零件?
20.方格纸上的图像表示轮船行驶的路程和时间的关系。这艘轮船2.5小时行驶了多少千米?8小时能行驶多少千米?
21.下面是某街区的平面示意图。
(1)火车站在钟楼的( )方向( )千米处。
(2)人民公园位于钟楼北偏西40°方向2千米处,请在图中标出大概的位置。
(3)小明的爸爸乘出租车从百货大楼经钟楼去火车站,要付费多少元?出租车收费标准如下:(不足1千米按1千米算)
里程 收费
3千米(含3千米)以下 8.00元
3千米以上每增加1千米 1.00元
22.《全品作业本》的总价与购买的本数如下表:
本数 1 2 3 4 5 6 …
总价/元 10 20 50 60 …
(1)把上面的表格补充完整。
(2)在下图中标出表中的数据对应的点,然后连接各点。你有什么发现?
(3)总价与本数之间有什么关系?为什么?
(4)如果购买15本《全品作业本》,需要( )元;480元钱可以购买( )本《全品作业本》。
23.装配1600台计算机,每天装配的台数和需要的天数如下表。
每天装配数量/台 40 80 100 160 200 400
需要的天数/天 40 20
(1)完成上面的表格。
(2)写出几组对应的每天装配的台数和需要的天数的乘积。
(3)这个乘积表示的是什么?用式子表示它们之间的关系。
(4)每天装配的台数和需要的天数成什么比例?为什么?
24.王江用计算机打字的个数和所用的时间如下表。
时间/分 2 4 6 8 10 12 14
数量/个 100 200 300 400 500 600 700
(1)根据表中的数据,在下图中描出打字数量和时间所对应的点,再把它们按顺序连接起来。
(2)王江打字的个数和所用的时间成正比例吗?你是根据什么来判断的?
(3)估计王江5分钟能打多少个字?打420个字要多少分钟?
参考答案:
1.A
【分析】判断两种相关联的量成不成比例,成什么比例,就看这两种量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,就成反比例,如果是其它的量一定或乘积、比值不一定,就不成比例。
【详解】A.正方体底面积一定,则正方体的棱长一定,体积也一定,所以正方体底面积一定,它的棱长与体积不成比例;
B.三角形的底×高=三角形的面积(一定),即底和高的乘积一定,所以三角形面积一定,它的底和高成反比例;
C.圆柱的侧面积÷底面周长=圆柱的高(一定),即圆柱的侧面积和底面周长的比值一定,所以圆柱的高一定,圆柱的侧面积和底面周长成正比例。
故答案为:A
【点睛】此题属于根据正、反比例的意义,辨识两种相关联的量成不成比例,成什么比例,就看这两种量是否都是变量,且对应的比值一定,或是对应的乘积一定,再做出判断。
2.C
【分析】判断两种相关联的量成不成比例,成什么比例,就看这两种量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,就成反比例,如果是其它的量一定或乘积、比值不一定,就不成比例。
【详解】由2x=y-4(y>4)可知:y-2x=4,乘积与比值均不一定,所以x和y不成比例。
故答案为:C
【点睛】此题属于根据正、反比例的意义,辨识两种相关联的量成不成比例,成什么比例,就看这两种量是否都是变量,且对应的比值一定,或是对应的乘积一定,再做出判断。
3.B
【分析】(1)判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例;
(2)本息=本金+利息,利息=本金×利率×时间,代入数据计算即可;
(3)2019年是平年,2月有28天,1、3月有31天,由此求出第一季度天数即可;
(4)半圆的周长=圆周长的一半+直径;据此逐项判断即可。
【详解】(1)每排的人数×排数=总人数(60名同学),也就是每排的人数与排数的乘积一定所以60名同学参加团体操表演,每排的人数和排数成反比例;原说法正确。
(2)5000+5000×3.75%×2
=5000+375
=5375(元)
到期时王奶奶可以取回5375元;原说法正确。
(3)2019年是平年,2月有28天,第一季度共31+28+31=90天;原说法错误。
(4)半圆的周长是它所在圆周长的一半+直径;原说法错误。
综上可知:正确说法有2个。
故答案为:B
【点睛】本题考查知识点较多,解题时注意半圆的周长与圆周长的关系。
4.B
【分析】判断小丽步行已走的路程与剩下的路程成不成比例,成什么比例,就看这两种量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,就成反比例,如果是其它的量一定或乘积、比值不一定,就不成比例.据此进行判断后再选择。
【详解】因为步行的路程+剩下的路程=从家到学校的路程(一定),
是对应的“和”一定,不是“乘积或比值”一定,
所以小丽步行已走的路程与剩下的路程不成比例。
故答案为:B。
【点睛】此题属于根据正、反比例的意义,辨识两种相关联的量成不成比例,成什么比例,就看这两种量是对应的比值一定,还是对应的乘积一定,还是对应的其它量一定,再做出判断。
5.C
【分析】把除法转化成乘法后,根据比例的基本性质写出比例,然后把后面的比化成最简整数比即可做出选择。
【详解】A×2=B÷3,则A×2=B×,那么A∶B=∶2=1∶6。
故答案为:C
【点睛】灵活运用比例的基本性质。
6.C
【分析】两个量成正比例关系,即一个量变化,另一个量也随之变化,但它们的比值是恒定的。
【详解】A.正方体的体积=棱长×棱长×棱长,它与棱长的比值并不是常数,所以该选项错误;
B.小明的身高会随着年龄变化而变化,但比值不是常数,所以选项错误;
C.汽车的耗油量=每公里耗油量×行程,它们的比值是恒定的,所以选项正确。
故答案选择C。
【点睛】本题考查的是两个量正比例关系的定义,准确判定两个量的比值否恒定是解题的关键。
7.
【分析】根据等式的性质,两边同时除以相同的数,等式仍然成立。
【详解】5a=3b
5a÷3a=3b÷3a
=
=
=
【点睛】熟练掌握等式的性质和比例的基本性质才是解此题的核心。
8. 正 正 反
【分析】判断两个相关联的量之间成什么比例,就看这两个量对应是的比值一定,还是对应的乘积一定;如果比值一定,就成正比例;如果乘积一定,则成反比例。
【详解】(1)根据比例的基本性质:两个内项的乘积等于两个外项的乘积。5a=9b可转变为比例的形式:a∶b=9∶5,即a÷b=,即a和b的比值一定,成正比例;
(2)=,进行交叉相乘,得:11x=7y,再根据比例的基本性质可转变为比例的形式:x∶y=7∶11,即x÷y=,即x和y的比值一定,成正比例;
(3)m∶3=10∶n, 根据比例的基本性质可转变为乘积的形式:mn=30,即m和n的乘积一定,成反比例。
故答案为:(1)正;(2)正;(3)反。
【点睛】熟练掌握的正比例和反比例的概念是解题的关键。
9. 反 正
【分析】判断两个相关联的量之间成什么比例,就看这两个量对应是的比值一定,还是对应的乘积一定;如果比值一定,就成正比例;如果乘积一定,则成反比例。
【详解】(1)每次运的块数×运砖次数=这批砖的总块数(一定),乘积一定,成反比例;
(2)比的前项÷比值=比的后项(一定),比值一定,成正比例。
故答案:(1)反;(2)正。
【点睛】熟练掌握的正比例和反比例的概念是解题的关键。
10. =k(一定)(x≠0) xy=k(一定)
【分析】正比例:相关联的两个量,比值一定。反比例:相关联的两个量,乘积一定。
【详解】如果用字母x和y表示两种相关联的量,用k表示它们的比值,正比例关系可以表示为( =k(一定)(x≠0) );如果用字母x和y表示两种相关联的量,用k表示它们的积,反比例关系可以表示为( xy=k(一定) )。
【点睛】熟练掌握的正比例和反比例的概念是解题的关键。
11. 反 正
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
【详解】(1)加工零件时间(一定)=每个零件加工时间×零件个数,乘积一定,成反比例;
(2)加工一个零件的时间(一定)=加工零件总个数÷加工零件时间,比值一定,成正比例。
【点睛】此题主要考查正、反比例的辨识,就看这两个量是对应的比值一定,还是对应的乘积一定,再做判断。
12.8
【分析】首先判断竹竿长与影长成什么比例,再通过比例求出旗杆的影长是6米时,算出旗杆的实际高度。判断两个相关联的量之间成什么比例,就看这两个量对应是的比值一定,还是对应的乘积一定;如果比值一定,就成正比例;如果乘积一定,则成反比例。
【详解】(1)1÷0.75=1÷=1×=;(2)1.2÷0.9=12÷9==;(4)1.6÷1.2=16÷12==;(4)2÷1.5=20÷15==;通过上述四个式子可以得知:竹竿长÷影长=(一定),竹竿长和影长的比值一定,成反比例。
当小红测量出校园中旗杆的影长是6米,即竹竿长∶影长=旗杆实际高度∶旗杆影长,设旗杆实际高度为X米。
可得:1∶0.75=X∶6
解:0.75X=6
X=6÷0.75
X=8
所以旗杆的实际高度是8米。
【点睛】熟练掌握的正、反比例的概念和比例的基本性质是解题的关键。
13.×
【分析】判断修了的米数和未修的米数是否成反比例,就看这两种量是否是对应的乘积一定,如果是乘积一定,就成反比例,如果不是乘积一定,就不成反比例。据此进行判断。
【详解】修了的米数+未修的米数=一条路的总米数(一定),是和一定,不是乘积一定,所以修了的米数和未修的米数不成反比例。
【点睛】此题属于辨识两种相关联的量是否成反比例,就看这两种量是否是对应的乘积一定,再做出判断。
14.×
【分析】判断两个相关联的量之间成什么比例,就看这两个量对应是的比值一定,还是对应的乘积一定;如果比值一定,就成正比例;如果乘积一定,则成反比例;无上述两种情况,则不成比例。
【详解】xy是两种相关联的量,且x-y=0(x与y都不为零),即x=y,所以x÷y=x∶y=1,即x和y的比值一定,成正比例。
故答案:×。
【点睛】熟练掌握的正、反比例的概念以及等式的变形是解题的关键。
15.×
【分析】两种相关联的量都是变量,且对应的乘积一定,就成反比例;对应的比值一定,就成正比例;否则就不成比例。
【详解】(a不等于0),5ab=8,ab=,即乘积一定,成反比例。
故答案为:×
【点睛】考查了正比例、反比例的意义和辨别,基础题。
16.√
【分析】比例尺=,比值一定,成正比例关系,据此解答。
【详解】根据分析可得,在1∶20000的地图上,图上距离和实际距离成正比例,原题说法正确。
故答案为:√
【点睛】在同一幅地图上,比例尺是定值,图上距离和实际距离成正比例关系,积一定是反比例关系。
17.√
【详解】题目中每天烧煤的吨数一定,烧煤的天数和烧煤的总吨数成正比例,由此可以找到两组对应数值:12和15,100和x,所以列出的算式是在正确的.
18.(1)x=200;(2)x=15;(3)x=1。
【分析】此题为解方程和解比例的题型,需注意解方程的步骤。解比例得按照比例的基本性质,两内项乘积等于两外项乘积。
【详解】(1)25%x+20%x=90
解:0.45x=90
x=90÷0.45
x=200;
(2)x∶=12∶
解:x=×12
x=3
x=3÷
x=15;
(3)x-40%x=
解:0.6x=0.6
x=0.6÷0.6
x=1。
【点睛】熟练掌握解方程的步骤和比例的基本性质并细心计算是解此题的关键。
19.①成正比例;因为生产的零件数与时间的比值一定
②5个
③0.5万个
【分析】(1)判断生产的零件数与时间是否成正比例,就看这两种量是否是对应的比值一定,如果是比值一定,就成正比例,如果不是比值一定或比值不一定,就不成正比例;
(2)先分别求出时间,再比较即可;
(3)由图意可知,2个月生产2万个零件,即可求出半个月加工多少个零件。
【详解】(1)由图意可知,工效是一定的,工效=工作总量÷工作时间,所以乙车间生产的零件数与时间成正比例;
(2)乙生产10万个零件需要:10÷2=5(个)
甲生产10万个零件需要:10÷(2÷2)=10(个)
10-5=5(个)
答:如果生产10万个零件,那么乙车间比甲车间少用5个月。
(3)2÷2÷2=0.5(万个)
答:甲车间半个月加工0.5万个零件。
【点睛】本题考查了比例的有关知识,解题的关键是从折线统计图中得到进一步解题的相关信息。
20.50千米;160千米
【分析】船的速度为20÷1=20(千米/时),根据路程=速度×时间,即可求出本题答案。
【详解】20÷1×2.5
=20×2.5
=50(千米)
20÷1×8
=20×8
=160(千米)
答:这艘轮船2.5小时行驶了50千米,8小时能行驶160千米。
【点睛】掌握路程=速度×时间,是解决问题的关键。
21.(1)正东;3
(2)
(3)10元
【分析】(1)、(2)东北方向也叫作北偏东,西北方向也叫作北偏西,西南方向叫作南偏西,东南方向叫作南偏东,再结合平面图即可得到具体位置。
(3)量得百货大楼到钟楼的图上距离是2厘米,线段比例尺已知,所以百货大楼到钟楼的实际距离为:2×1=2(千米),火车站离钟楼的实际距离为:3×1=3(千米),所以总距离为3+2=5(千米),因为3千米(含3千米)以下,收费8元,所以有5-3=2(千米)是收费1元的,即可求出总的付费钱数。
【详解】(1)火车站在钟楼的正东方向3千米处。
(2)根据线段比例尺结合方向位置的描述可以画出来。
(3)量得百货大楼到钟楼的图上距离是2厘米。
1×2=2(千米)
2+3=5(千米)
(5-3)×1+8
=2×1+8
=2+8
=10(元)
答:小明的爸爸乘出租车从百货大楼经钟楼去火车站,要付费10元。
【点睛】掌握线段比例尺的定义是本题的解题关键。
22.(1)30;40
(2)
是一条过(0,0)点的直线。(发现合理即可)
(3)总价和本数成正比例关系,因为总价和本数是相关联的量,并且=单价(一定)。
(4)150;48
【分析】(1)因为10÷1=10,20÷2=10,50÷5=10,60÷6=10,所以根据=单价,可知单价为10元,即可求出当本数为3本、4本时候的总价。
(2)将描出的点顺次连接,得到的是一条过(0,0)点的直线。
(3)=单价,如果两种相关联的量,它们的比值是一定的,则这两种量是成正比例的量,它们的关系叫作正比例关系。
(4)根据总价=单价×本数,进行求解。
【详解】(1)因为=单价,且单价为10元,所以30÷3=10,40÷4=10,所以当本数为3本、4本的时候总价为30元、40元。
(2)通过描点连线得到的是一条过原点的直线。
(3)因为=单价,且单价一定,根据正比例关系的定义,所以两者是正比例关系。
(4)因为单价为10元,所以买15本需要15×10=150(元);用480元可以买480÷10=48(本)。
【点睛】此题考查了正比例关系的定义和总价=单价×本数的应用。
23.(1)
每天装配数量/台 40 80 100 160 200 400
需要的天数/天 40 20 16 10 8 4
(2)40×40=1600(台);80×20=1600(台);100×16=1600(台)等;
(3)这个乘积表示的是需要装配的计算机的台数,计算机的台数=每天装配的台数×需要的天数;
(4)成反比例,因为每天装配的台数×需要的天数=计算机的台数,乘积一定。
【分析】(1)利用总数量1600除以每天装配的数量即可求出对应的天数,完成表格;
(2)(3)根据题意写出几组每天的台数和需要的天数的乘积,计算出答案,然后结合表格写出乘积表示什么,表示出这个关系;
(4)仔细观察,看(3)中的乘积是不是定值,进而判断比例关系。
【详解】(1)40×40=1600(台);1600÷80=20(天);1600÷100=16(天);1600÷160=10(天);1600÷200=8(天);1600÷400=4(天)
每天装配数量/台 40 80 100 160 200 400
需要的天数/天 40 20 16 10 8 4
(2)40×40=1600(台);80×20=1600(台);100×16=1600(台)等;
(3)这个乘积表示的是需要装配的计算机的台数,计算机的台数=每天装配的台数×需要的天数;
(4)成反比例。因为每天装配的台数×需要的天数=计算机的台数,乘积一定。
【点睛】本题考查了正反比例的知识,清楚正反比例的意义是解题的关键。
24.(1)
(2)成正比例;
依据:打字的个数和所用时间是两个相关联的量,打字的个数随着所用时间的变化而变化,即打字的个数与所用时间的比值一定,所以打字的个数和所用时间成正比例。
(3)250个;8.4分钟
【分析】(1)根据横轴表示时间,纵轴表示打字个数描点,再连线即可;
(2)观察可知打字数量随时间的变化而变化,而每分钟打字个数不变,据此解答;
(3)先求出每分钟打字的个数,再根据乘除法的意义可完成解答。
【详解】(1)
(2)成正比例,依据:打字的个数和所用时间是两个相关联的量,打字的个数随着所用时间的变化而变化,即打字的个数与所用时间的比值一定,所以打字的个数和所用时间成正比例。
(3)(100÷2)×5
=50×5
=250(个)
450÷(100÷2)
=750÷50
=8.4(分钟)
答:王江5分钟能打250个字,打420个字要8.4分钟。
【点睛】本题是关于正反比例的题目,掌握正反比例的意义是关键。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
