一次函数图象和性质练习题

一、一次函数的定义
1、选择题
（1）下列说法不正确的是（ ）
A．一次函数不一定是正比例函数。B．不是一次函数就不一定是正比例函数。
C．正比例函数是特殊的一次函数。D．不是正比例函数就一定不是一次函数。
（2）下列函数中一次函数的个数为（ ( http: / / www.21cnjy.com ) ）①y=2x；②y=3+4x；③y=1/2；④y=ax（a≠0的常数）；⑤xy=3； ⑥2x+3y-1=0；A．3个 B 4个 C 5个 D 6个
(3 )设圆的面积为s，半径为R,那么下列说法正确的是（ ）
A S是R的一次函数 B S是R的正比例函数 C S是的正比例函数D 以上说法都不正确
2、填空题
（1）若函数y=(m-2)x+5是一次函数，则m满足的条件是____________。
（2）当m=__________时，函数y=3x2m+1 +3 是一次函数。
(3 )关于x的一次函数y=x+5m-5，若使其成为正比例函数，则m应取_________。
（4）已知函数y=当m= 时，y是x的一次函数？当m= ，y是x的正比例函数。
(5)函数：①y=-2x+3；②x+y=1；③xy=1；④y=；⑤y=+1；⑥y=0.5x中，属一次函数的有 ，属正比例函数的有 （只填序号）
（6）当m= 时，y=是一次函数。
(7)请写出一个正比例函数，且x=2时， ( http: / / www.21cnjy.com )y= －6 ,请写出一个一次函数，且x=－6时，y=2
(8) 我国是一个水资源缺乏的国家，大家要 ( http: / / www.21cnjy.com )节约用水．据统计，拧不紧的水龙头每秒钟会滴下2滴水，每滴水约0.05毫升．李丽同学在洗手时，没有把水龙头拧紧，当李丽同学离开x小时后水龙头滴了y毫升水．则y与x之间的函数关系式是
(9) 汽车以40千米/小 ( http: / / www.21cnjy.com )时的平均速度从A站出发，行驶了t小时，那么汽车离开A站的距离s(千米)和时间t(小时)之间的函数关系是什么？的函数关系式为 ，它是 函数
(10) 汽车离开A站4千米，再以40 ( http: / / www.21cnjy.com )千米／小时的平均速度行驶了t小时，那么汽车离开A站的距离s(千米)与时间t(小时)之间的函数关系是什么？的函数关系式为 ，它是 函数
3、甲市到乙市的包裹邮资为每千克0 ( http: / / www.21cnjy.com ).9元，每件另加手续费0.2元，求总邮资y（元）与包裹重量x（千克）之间的函数解析式，并计算5千克重的包裹的邮资。
4、在拖拉机油箱中，盛满56千克油 ( http: / / www.21cnjy.com )，拖拉机工作时，每小时平均耗油6千克，求邮箱里剩下Q（千克）与拖拉机的工作时间t（小时）之间的函数解析式。
二、 一次函数的图象
1、直线y=2x＋5与直线，都经过y轴上的同一点（ 、 ）
2、（1）一次函数y=kx+b当x=0时，y= ， 横坐标为0点在 上；当y=0时，x= ，纵坐标为0点在 上。 画一次函数的图象时，常选取（0, ）、（ , 0）两点连线；（2）直线y＝4x－3过点（_____，0）、（0， ）；（3）直线过点（ ，0）、（0， ）．
3、 分别在同一直角坐标系内画出下列直线，写出各直线分别与x轴、y轴的交点坐标，并指出每一小题中两条直线的位置关系．
（1）y=－x+2 ； y=－x－1.
（2）y=3x－2 ； y=.
直线y=－x+2与x轴的交点坐标是 ，与y轴的交点坐标是 　　 ；直线y=－x－1与x轴的交点坐标是 ，与y轴的交点坐标是 　　
直线y=4x－2与x轴的交点坐标是 ，与y轴的交点坐标是 　　 ；直线y=与x轴的交点坐标是 ，与y轴的交点坐标是 　　
4、 画出函数y＝－2x＋3的图象，借助图象找出：
直线上横坐标是2的点，它的坐标是（ ， ）
线上纵坐标是－3的点，它的坐标是（ ， ）；（3）直线上到y轴距离等于2的点，它的坐标是（ ， ）；（4）点（2、7）是否在此图象上；（ ）；（5）找出到轴的距离等于1的点，并标出其坐标；（ ， ）（6）找出图象与轴和轴的交点，并标出其坐标。（ ， ）
三、一次函数的性质
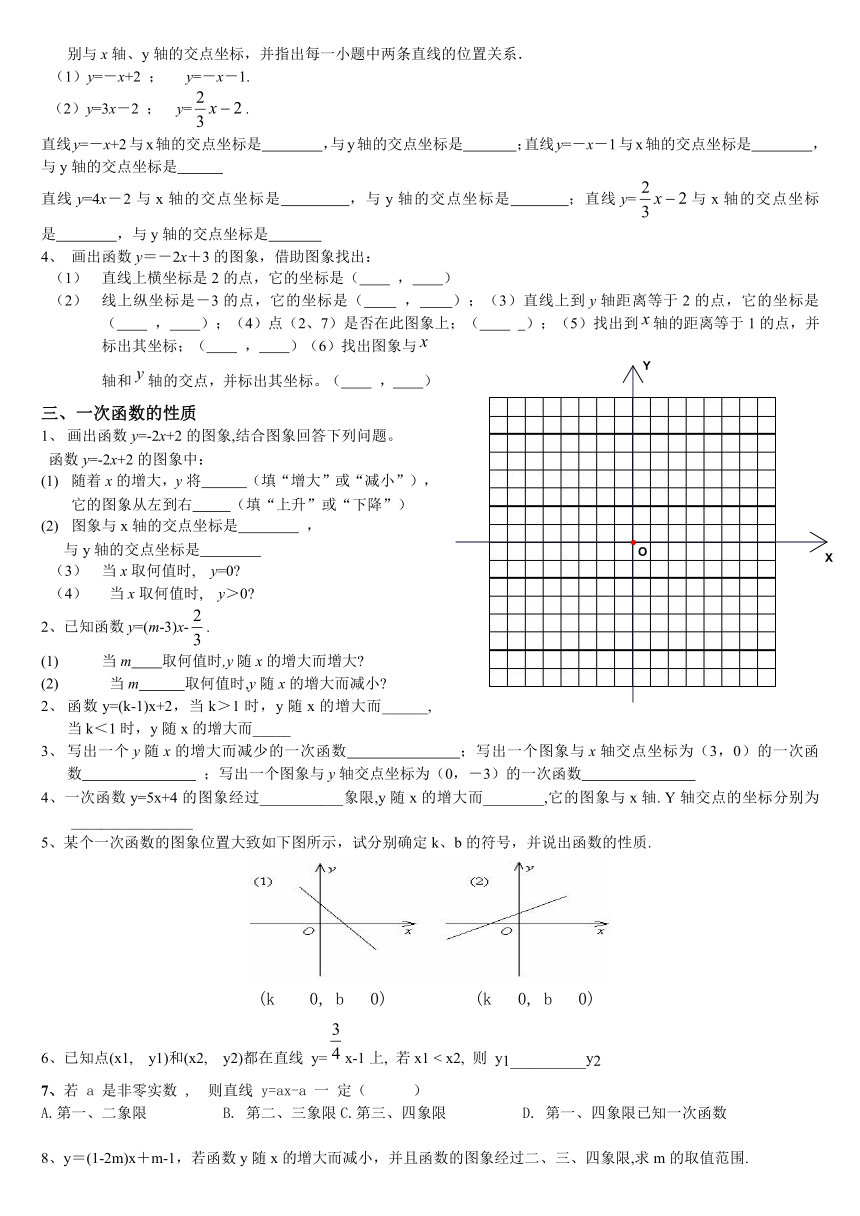
画出函数y=-2x+2的图象,结合图象回答下列问题。
函数y=-2x+2的图象中：
随着x的增大，y将 （填“增大”或“减小”），
它的图象从左到右 （填“上升”或“下降”）
图象与x轴的交点坐标是 ，
与y轴的交点坐标是
当x取何值时, y=0
当x取何值时, y＞0
2、已知函数y=(m-3)x-.
当m 取何值时,y随x的增大而增大
当m 取何值时,y随x的增大而减小
函数y=(k-1)x+2，当k＞1时，y随x的增大而______,当k＜1时，y随x的增大而_____
写出一个y随x的增大而减少 ( http: / / www.21cnjy.com )的一次函数 ；写出一个图象与x轴交点坐标为（3，0）的一次函数 ；写出一个图象与y轴交点坐标为（0，－3）的一次函数
4、一次函数y=5x+4 ( http: / / www.21cnjy.com )的图象经过___________象限,y随x的增大而________,它的图象与x轴. Y轴交点的坐标分别为________________
5、某个一次函数的图象位置大致如下图所示，试分别确定k、b的符号，并说出函数的性质.
( http: / / www.21cnjy.com )
(k 0, b 0) (k 0, b 0)
6、已知点(x1, y1)和(x2, y2)都在直线 y=x-1上, 若x1 < x2, 则 y1__________y2
7、若 a 是非零实数 , 则直线 y=ax-a 一 定（ ）
A.第一、二象限 B. 第二、三象限C.第三、四象限 D. 第一、四象限已知一次函数
8、y＝(1-2m)x＋m-1，若函数y随x的增大而减小，并且函数的图象经过二、三、四象限,求m的取值范围.
9、已知一次函数y＝（1－2k） x＋ ( http: / / www.21cnjy.com )（2k＋1）①当k取何值时，y随x的增大而增大？②当k取何值时，函数图象经过坐标系原点？③当k取何值时，函数图象不经过第四象限？
10、已知函数y＝2x-4.(1)作出它的图象；(2)标出图象与x轴、y轴的交点坐标；由图象观察，当-2≤x≤4时，函数值y的变化范围.
11、已知函数,当m为何值时，这个函数是一次函数.并且图象经过第二、三、四象限？
12、 已知一次函数y＝(3m-8)x ( http: / / www.21cnjy.com )＋1-m图象与y轴交点在x轴下方，且y随x的增大而减小，其中m为整数.(1)求m的值；(2)当x取何值时，0＜y＜4？
四、 一次函数图象和性质
1、 已知函数轴交点的纵坐标为，且当，则此函数的解析式为　　　　　　　　　．
2、 在函数中，函数随着的增大而　　，此函数的图象经过点，则　　　　　．
3、一次函数与的图象交于轴上一点，则　　　　．
4、 在下列四个函数中，的值随值的增大而减小的是（　　）
Ａ． Ｂ． Ｃ． Ｄ．
5、在下列函数中，（　　）的函数值先达到100．
Ａ． Ｂ． Ｃ． Ｄ．
6、已知一次函数，其在直角坐标系中的图象大体是（　　）
7、如图，表示一次函数与正比例函数（为常数，且）图象的是（　　）
8、已知一次函数的图象不经过第三象限，也不经过原点，那么的取值范围是（　　）
Ａ．且 Ｂ．且 Ｃ．且 Ｄ．且
9、、 如图所示，已知正比例函数的函数值随的增大而增大，则一次函数的图象大致是（　　）
10、 若函数与轴的交点在轴的上方，且为整数，则符合条件的有（　　）
Ａ．8个 Ｂ．7个 Ｃ．9个 Ｄ．10个
11、已知一次函数的图象经过一、二、四象限，求的取值范围．
12、已知一次函数，且的值随值的增大而增大．（1）的范围；（2）若此一次函数又是正比例函数，试求的值．
五、一次函数与一元一次方程
直线与x轴交点的横坐标，就是一元一次方程的解。求直线与x轴交点时，可令，得到方程，解方程得，直线交x轴于，就是直线与x轴交点的横坐标
1、已知直线和交于轴上同一点，的值为（ ）
A. B． C． D．
2、已知一次函数与的图象相交于点，则______．
3、已知一次函数的经过点，，则不求，可直接得到方程的解是 ．
六、一次函数与二元一次方程
一次函数的解析式本身就是一个二元一次方程，直线上有无数个点，每个点的横纵坐标都满足二元一次方程，因此二元一次方程的解也就有无数个。
1、已知直线与的交点为（-5，-8），则方程组的解是________．该方程组的解具有怎样的几何意义？
2、已知方程组（为常数，）的解为，则直线和直线的交点坐标为___ _____．
3、已知是方程组的解，那么一次函数_____和_____的交点是____
4、b取什么整数值时，直线与直线的交点在第二象限？
5、直线l1的解析表达式为：y=-3x+3，且l1与x轴交于点D，直线l2经过点A，B，
直线l1，l2交于点C．
（1）求点D的坐标；（2）求直线l2的解析表达式；
（3）求△ADC的面积；
（4）在直线l2上存在异于点C的另一点P，使得△ADP与△ADC的面积相等，请直接写出点P的坐标．
（5）在x轴上求作一点M，使得BM+CM的和最小，直接写出M点的坐标
七、一次函数与一元一次不等式的关系
任何一元一次不等式都可以转化为或(为常数，)的形式，所以
解一元一次不等式可以看作：当一次函数值大（小）于0时，求自变量相应的取值范围。
1、已知，．当时，x的取值范围是（ ）
A． B． C． D．
2、一次函数（是常数，）的图象如图所示，则不等式的
解集是（ ）
A． B． C． D．
3、如图，已知直线经过点A(-1，-2)和点B(-2，0)，直线经过点A，
则不等式的解集为( )
A. B. C. D.
4、直线与直线在同一平面直角坐标系中的图象如图所示，
则关于的不等式的解集为______．
5、若解方程得，则当x_________时直线上的点在直线上相应点的上方．
6、已知一次函数（1）当取何值时，函数的值在与之间变化
（2）当从到3变化时，函数的最小值和最大值各是多少
7、当自变量满足什么条件时，函数的图象在：（1）轴上方；（2）轴左侧；（3）第一象限．
八、一次函数的应用
1、某天小明骑自行车上学，途中因自行车发生故障，修车耽误了一段时间后继续骑车前行，并按时赶到了学校．
如图描述了他上学途中的情景，下列说法中错误的是( )
A. 修车时间为15分钟
B. 学校离家的距离为2000米
C. 从家到学校共用时20分钟
D. 自行车发生故障时离家的距离为1000米
2、已知A，B两城相距600千米，甲、乙两车同时从A城出发驶向B城，甲车到达B城后立即沿原路返回．如图是它们离A城的距离
y（千米）与行驶时间x（小时）之间的函数关系，若当两车相遇时，
它们行驶了7小时，则下列说法中正确的是( )
A、乙车的速度比甲车的速度快 B.F点的坐标为（7，500）
C.乙车的速度为75千米/小时
D. 甲车在行驶过程中y与x之间的函数关系式为y=100x
3、某食品加工厂，准备研制加工两种 ( http: / / www.21cnjy.com )口味的核桃巧克力，即原味核桃巧克力和益智核桃巧克力．现有主要原料可可粉410克，核桃粉520克．计划利用这两种主要原料，研制加工上述两种口味的巧克力共50块．加工一块原味核桃巧克力需可可粉13克，需核桃粉4克；加工一块益智核桃巧克力需可可粉5克，需核桃粉14克．加工一块原味核桃巧克力的成本是1.2元，加工一块益智核桃巧克力的成本是2元．设这次研制加工的原味核桃巧克力x块．
（1）求该工厂加工这两种口味的巧克力有哪几种方案？
（2）设加工两种巧克力的总成本为y元，求y与x的函数关系式，并说明哪种加工方案使总成本最低？总成本最低是多少元？
Ｏ
ｙ
ｘ
Ｏ
ｙ
ｘ
Ｏ
ｙ
ｘ
Ｏ
ｙ
ｘ
Ｄ．
Ｃ．
B．
A．
Ｏ
x
y
x
y
Ｏ
x
y
Ｏ
x
y
Ｏ
Ａ．
Ｂ．
C．
D．
Ｏ
x
y
Ｏ
x
y
Ｏ
x
y
Ｏ
x
y
D．
Ｃ．
B．
A．