2022-2023学年湖北省武汉市东西湖区常青第一学校九年级(下)月考数学试卷(3月份)(含解析)
文档属性
| 名称 | 2022-2023学年湖北省武汉市东西湖区常青第一学校九年级(下)月考数学试卷(3月份)(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 616.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-13 08:56:42 | ||
图片预览


文档简介
2022-2023学年湖北省武汉市东西湖区常青第一学校九年级(下)月考数学试卷(3月份)
一、选择题(本大题共9小题,共27.0分。在每小题列出的选项中,选出符合题目的一项)
1. 下列说法正确的是( )
A. 为了解我国中小学生的睡眠情况,应采取全面调查的方式
B. 一组数据,,,,,,的众数和平均数都是
C. 若甲、乙两组数据的方差分别是,,则甲组数据比乙组数据更稳定
D. 抛掷一枚硬币次,一定有次“正面向上”
2. 下列图形中,既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
3. 下列计算正确的是( )
A. B. C. D.
4. 由个大小相同的小正方体搭成的几何体如图所示,它的主视图是( )
A.
B.
C.
D.
5. 在反比例函数的图象的每一支上,都随的增大而减小,且整式是一个完全平方式,则该反比例函数的解析式为( )
A. B. C. D.
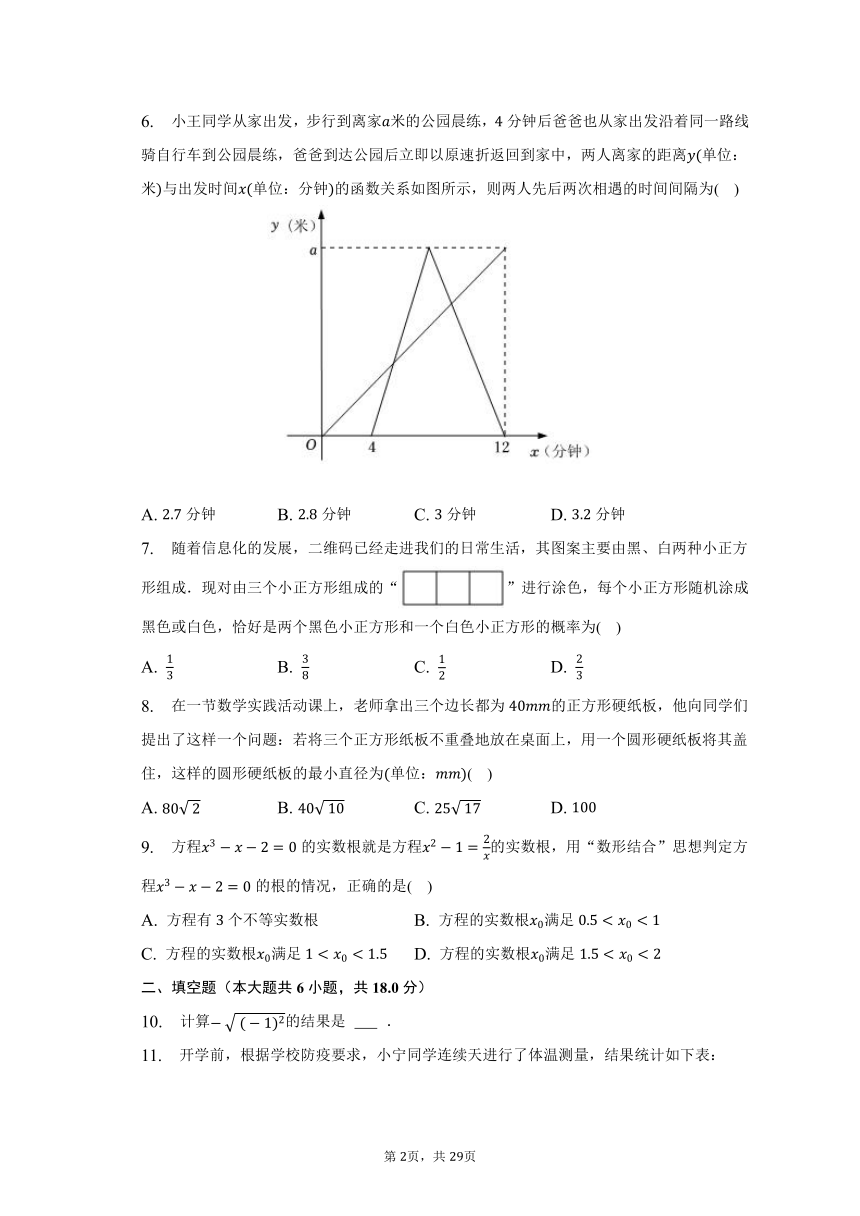
6. 小王同学从家出发,步行到离家米的公园晨练,分钟后爸爸也从家出发沿着同一路线骑自行车到公园晨练,爸爸到达公园后立即以原速折返回到家中,两人离家的距离单位:米与出发时间单位:分钟的函数关系如图所示,则两人先后两次相遇的时间间隔为( )
A. 分钟 B. 分钟 C. 分钟 D. 分钟
7. 随着信息化的发展,二维码已经走进我们的日常生活,其图案主要由黑、白两种小正方形组成.现对由三个小正方形组成的“”进行涂色,每个小正方形随机涂成黑色或白色,恰好是两个黑色小正方形和一个白色小正方形的概率为( )
A. B. C. D.
8. 在一节数学实践活动课上,老师拿出三个边长都为的正方形硬纸板,他向同学们提出了这样一个问题:若将三个正方形纸板不重叠地放在桌面上,用一个圆形硬纸板将其盖住,这样的圆形硬纸板的最小直径为单位:( )
A. B. C. D.
9. 方程的实数根就是方程的实数根,用“数形结合”思想判定方程的根的情况,正确的是( )
A. 方程有个不等实数根 B. 方程的实数根满足
C. 方程的实数根满足 D. 方程的实数根满足
二、填空题(本大题共6小题,共18.0分)
10. 计算的结果是 .
11. 开学前,根据学校防疫要求,小宁同学连续天进行了体温测量,结果统计如下表:
体温
天数天
这天中,小宁体温的中位数为 .
12. 方程的解是 .
13. 如图,有甲乙两座建筑物,从甲建筑物点处测得乙建筑物点的俯角为,点的俯角为,为两座建筑物的水平距离.已知乙建筑物的高度为,则甲建筑物的高度为______
,结果保留整数.
14. 已知二次函数的部分图象如图所示,对称轴为直线,有以下结论:;若为任意实数,则有;当图象经过点时,方程的两根为,,则,其中,其中正确的是 填写序号.
15. 如图,中,,是外面的一点,连接,,且,,,则的长为 .
三、解答题(本大题共8小题,共72.0分。解答应写出文字说明,证明过程或演算步骤)
16. 本小题分
解不等式组请按下列步骤完成解答.
解不等式,得______;
解不等式,得______;
把不等式和的解集在数轴上表示出来;
原不等式组的解集是______.
17. 本小题分
如图,平行四边形中,点、在对角线上,且求证:
≌;
四边形是平行四边形.
18. 本小题分
为落实“双减”政策,优化作业管理,某中学从全体学生中随机抽取部分学生,调查他们每天完成书面作业的时间单位:分钟按照完成时间分成五组:组“”,组“”,组“”,组“”,组“”将收集的数据整理后,绘制成如下两幅不完整的统计图.
根据以上信息,解答下列问题:
这次调查的样本容量是______,请补全条形统计图;
在扇形统计图中,组的圆心角是______度,本次调查数据的中位数落在______组内;
若该校有名学生,请你估计该校每天完成书面作业不超过分钟的学生人数.
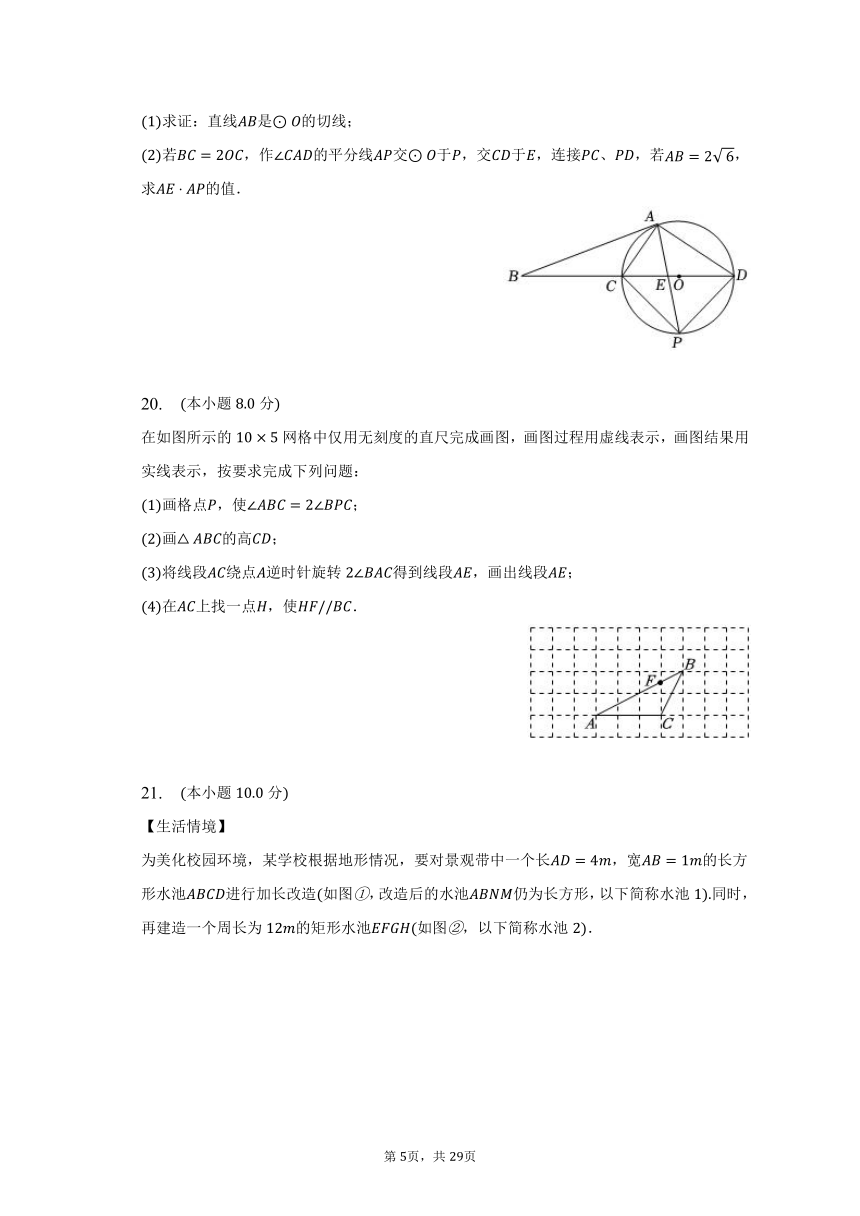
19. 本小题分
如图是直径,是上异于,的一点,点是延长线上一点,连、、,且.
求证:直线是的切线;
若,作的平分线交于,交于,连接、,若,求的值.
20. 本小题分
在如图所示的网格中仅用无刻度的直尺完成画图,画图过程用虚线表示,画图结果用实线表示,按要求完成下列问题:
画格点,使;
画的高;
将线段绕点逆时针旋转得到线段,画出线段;
在上找一点,使.
21. 本小题分
【生活情境】
为美化校园环境,某学校根据地形情况,要对景观带中一个长,宽的长方形水池进行加长改造如图,改造后的水池仍为长方形,以下简称水池同时,再建造一个周长为的矩形水池如图,以下简称水池.
【建立模型】
如果设水池的边加长长度为,加长后水池的总面积为,则关于的函数解析式为:;设水池的边的长为,面积为,则关于的函数解析式为:,上述两个函数在同一平面直角坐标系中的图像如图.
【问题解决】
若水池的面积随长度的增加而减小,则长度的取值范围是______可省略单位,水池面积的最大值是______;
在图字母标注的点中,表示两个水池面积相等的点是______,此时的值是______;
当水池的面积大于水池的面积时,的取值范围是______;
在范围内,求两个水池面积差的最大值和此时的值;
假设水池的边的长度为,其他条件不变这个加长改造后的新水池简称水池,则水池的总面积关于的函数解析式为:若水池与水池的面积相等时,有唯一值,求的值.
22. 本小题分
同学们还记得吗?图,图是人教版八年级下册教材“实验与探究”中我们研究过的两个图形.受这两个图形的启发,数学兴趣小组提出了以下三个问题,请你回答:
【问题一】如图,正方形的对角线相交于点,点又是正方形的一个顶点,交于点,交于点,则与的数量关系为______;
【问题二】受图启发,兴趣小组画出了图:直线、经过正方形的对称中心,直线分别与、交于点、,直线分别与、交于点、,且,若正方形边长为,求四边形的面积;
【问题三】受图启发,兴趣小组画出了图:正方形的顶点在正方形的边上,顶点在的延长线上,且,在直线上是否存在点,使为直角三角形?若存在,求出的长度;若不存在,说明理由.
23. 本小题分
抛物线与直线交于原点和点,与轴交于另一点,顶点为.
直接写出点和点的坐标;
如图,连接,为轴上的动点,当时,求点的坐标;
如图,是点关于抛物线对称轴的对称点,是抛物线上的动点,它的横坐标为,连接,,与直线交于点设和的面积分别为和,求的最大值.
答案和解析
1.【答案】
【解析】解:为了解我国中小学生的睡眠情况,应采取抽样调查的方式,故本选项不合题意;
B.数据,,,,,,的众数是平均数为,故本选项不合题意;
C.若甲、乙两组数据的方差分别是,,则甲组数据比乙组数据更稳定,说法正确,故本选项符合题意;
D.抛掷一枚硬币次,不一定有次“正面向上”,故本选项不合题意;
故选:.
选项A根据抽样调查和全面调查的意义判断即可;选项B根据众数和平均数的定义判断即可;选项C根据方差的意义判断即可;选项D根据随机事件的定义判断即可.
本题考查了方差,众数,平均数以及全面调查与抽样调查,掌握相关定义是解答本题的关键.
2.【答案】
【解析】解:、该字母不是中心对称图形,是轴对称图形,故此选项不合题意;
B、该字母不是中心对称图形,是轴对称图形,故此选项不合题意;
C、该字母是中心对称图形,不是轴对称图形,故此选项不合题意;
D、该字母既是轴对称图形又是中心对称图形,故此选项符合题意;
故选:.
根据中心对称图形与轴对称图形的概念进行判断即可.
本题考查的是中心对称图形与轴对称图形的概念.轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合,中心对称图形是要寻找对称中心,旋转度后与自身重合.
3.【答案】
【解析】解:,故A错误,不符合题意;
,故B错误,不符合题意;
,故C正确,符合题意;
,故D错误,不符合题意;
故选:.
根据同底数幂的乘除、幂的乘方与积的乘方、合并同类项法则逐项判断.
本题考查整式的运算,解题的关键是掌握整式运算的相关法则.
4.【答案】
【解析】解:从正面看,底层是三个小正方形,上层的左边是一个小正方形,
故选:.
根据从正面看得到的图形是主视图,可得答案.
本题考查了简单组合体的三视图.解题的关键是理解简单组合体的三视图的定义,明确从正面看得到的图形是主视图.
5.【答案】
【解析】解:在反比例函数的图象的每一支上,都随的增大而减小,
,则,
整式是一个完全平方式,
,则,
,
该反比例函数的解析式为,
故选:.
先根据反比例函数的性质得到,再根据完全平方式的特点求得,进而求得即可求解.
本题考查反比例函数的图象与性质、完全平方式,熟知完全平方式的结构是解答的关键.
6.【答案】
【解析】解:由图象可得,
小明的速度为米分钟,
爸爸的速度为:米分钟,
设小明出发分钟两人第一次相遇,出发分钟两人第二次相遇,
,,
解得,,
,
故选:.
根据题意和函数图象中的数据,可以先表示出两人的速度,然后即可计算出两人第一次和第二次相遇的时间,然后作差即可.
本题考查一次函数的应用,解答本题的关键是明确题意,求出两人相遇的时间.
7.【答案】
【解析】解:画树状图如下:
由树状图知,共有种等可能结果,其中恰好是两个黑色小正方形和一个白色小正方形的有种结果,
所以恰好是两个黑色小正方形和一个白色小正方形的概率为,
故选:.
画树状图得出所有等可能结果,从中找到符合条件的结果数,再根据概率公式求解即可.
本题主要考查列表法与树状图法求概率,列举法树状图法求概率的关键在于列举出所有可能的结果,列表法是一种,但当一个事件涉及三个或更多元素时,为不重不漏地列出所有可能的结果,通常采用树状图.
8.【答案】
【解析】解:如图所示:设圆心为,与交点为,连接、、,
垂直平分,,
在上,,
设,则,
在中,
在中,
解得:,
则,
圆形硬纸板的最小直径为,
故选:.
连接、、,设,根据勾股定理列出关于的方程,解方程得到答案.
本题考查的是正多边形和圆的有关计算,掌握正方形的性质、勾股定理、垂径定理是解题的关键.
9.【答案】
【解析】解:方程的实数根就是方程的实数根,
方程的根可以看作是:与两函数的交点的横坐标,
函数和函数的图象如图,
观察图象,函数和函数的图象有一个交点,交点的横坐标在范围内,
所以,方程的实数根满足.
故选:.
画出函数和函数的图象,观察交点情况,即可判断方程的根的情况.
本题考查的是反比例函数及二次函数的图象,根据判别式及高次方程,利用数形结合求解是解题的关键.
10.【答案】
【解析】解:,
故答案为:.
根据二次根式的性质求解即可.
本题考查二次根式的性质,熟练掌握二次根式的性质是解答的关键,注意符号问题.
11.【答案】
【解析】解:在所给个数据中,第和第个的数据均为,
小宁体温的中位数为,
故答案为:.
根据中位数的定义求第和第个的数据的平均数即可.
本题考查中位数,解答关键是熟知中位数是一组数据从小到大或从大到小重新排列后,若数据是奇数个,则中位数是最中间的那个数,如果数据是偶数个,则中位数是最中间两个数的平均数,注意先进行排序.
12.【答案】
【解析】
【分析】
此题考查了解分式方程,利用了转化的思想,解分式方程时注意要检验.
分式方程去分母转化为整式方程,求出整式方程的解得到的值,经检验即可得到分式方程的解.
【解答】
解:去分母得:,
解得:,
经检验是分式方程的解.
故答案为:.
13.【答案】
【解析】解:过点作于点,如图.
则,,,
在中,,
设,则,
,,
在中,
,
解得,
.
故答案为:.
过点作于点,则,,,在中,,设,则,,,在中,,解得,进而可得出答案.
本题考查解直角三角形的应用仰角俯角问题,熟练掌握锐角三角函数的定义是解答本题的关键.
14.【答案】
【解析】解:抛物线的开口向上,与轴负半轴相交,
,,
抛物线的对称轴为直线,
,
,
,
故正确;
当时,有最小值,
为任意实数,
即,
故正确;
图象经过点,对称轴为直线,
二次函数图象经过另一个点,
即二次函数与直线的交点为和,
方程的两个根为,,
,
故正确,
综上,正确的是,
故答案为:.
根据抛物线的开口方向和对称轴方程、与轴的交点可判断;利用时取得最小值可判断;由抛物线与直线的交点以及抛物线的对称性可判断,进而可得结论.
本题考查二次函数图象与系数的关系,掌握二次函数的性质,数形结合思想求解是解答的关键.
15.【答案】
【解析】解:作于点,交于点,连接,
,
,
,即,
设,,则,,,,
,即,
∽,
,,
,,
即,
在中,,即,
解得,
.
故答案为:.
作于点,交于点,连接,由,设,,则,,,,推出∽,求得,,在中,利用勾股定理即可求解.
本题考查了解直角三角形,相似三角形的判定和性质,勾股定理等,作出辅助线,证明∽是解题的关键.
16.【答案】解:;
;
如图所示:
.
【解析】解:解不等式,得:;
解不等式,得:;
把不等式和的解集在数轴上表示出来为:
原不等式组的解集为:.
故答案为:;
;
.
分别解这两个不等式,把不等式和的解集在数轴上表示出来,找到解集的公共部分即可得到原不等式组的解集.
本题考查了解一元一次不等式组,在数轴上表示不等式的解集,体现了数形结合的思想,在数轴上找到解集的公共部分是解题的关键.
17.【答案】证明四边形是平行四边形,
,
,
,
≌ ;
证明:由知,≌,
,,
,
,
四边形是平行四边形.
【解析】根据平行四边形平行四边形的性质得到 ,从而得到,然后利用证得两三角形全等即可;
利用中的全等三角形的对应角相等推知,则等角的补角相等,即,所以根据“有一组对边平行且相等”证得结论.
本题考查了全等三角形的判定与性质,平行四边形的判定与性质.平行四边形的判定方法共有五种,应用时要认真领会它们之间的联系与区别,同时要根据条件合理、灵活地选择方法.
18.【答案】,
补全的条形统计图如图所示:
;;
人,
答:估计该校每天完成书面作业不超过分钟的学生有人.
【解析】解:这次调查的样本容量是:,
组的人数为:人,
故答案为:;
在扇形统计图中,组的圆心角是:,
本次调查了个数据,第个数据和个数据都在组,
中位数落在组,
故答案为:;;
见答案.
根据组的人数和所占的百分比,可以计算出本次调查的人数,然后即可计算出组的人数,从而可以将条形统计图补充完整;
根据统计图中的数据,可以计算出组的圆心角的度数,以及中位数落在哪一组;
根据题意和统计图中的数据,可以计算出该校每天完成书面作业不超过分钟的学生人数.
本题考查条形统计图、扇形统计图、用样本估计总体、中位数,解答本题的关键是明确题意,利用数形结合的思想解答.
19.【答案】证明:连接,
是直径,
,则,
,
,
又,
,即,
是半径,
直线是的切线;
解:设,
,
,,
在中,,,
,解得或舍去,
,,
∽,
,则,
在中,,
,,
平分,
,
又,
∽,
,
.
【解析】连接,先利用圆周角定理得到,再根据等腰三角形的性质结合已知可证得,然后根据切线的判定可证得结论;
设,根据勾股定理求出,再证明∽,然后利用相似三角形的性质得到,再次利用勾股定理求得,,证明∽,得到求解即可.
本题考查圆周角定理、切线的判定、等腰三角形的性质、相似三角形的判定与性质、勾股定理、角平分线的定义等知识,熟练掌握相关知识的联系与运用,会利用相似三角形的性质求解是解答的关键.
20.【答案】解:方法一:如图,取格点,连接,则,
,
,
故点即为所求作;
方法二:还可取格点,连接,,则,
,
根据网格特点和全等三角形的性质得,
,
故点即为所求作;
取格点,连接交于,
则即为所求作的高;
理由:由网格特点,,
则,
,与相交,
,
即;
取格点、,连接交于,连接,则线段即为所求作;
理由:根据网格特点,,则,
,
,则,又,
垂直平分,
,即;
取格点、,连接交于,连接,则,故点即为所求.
理由:根据网格特点,,
即,又,
∽,
,
.
【解析】取格点,连接,则,根据等腰三角形的性质和三角形的外角性质可求解;还可取格点,连接,,则,,再根据网格特点和全等三角形的性质得到平分,进而可得到;
取格点,连接交于,由网格特点,证明,根据三角形的内角和定理和对顶角相等证得即可;
取格点、,连接交于,连接,根据网格特点,证明得到,根据平行线分线段成比例可得,进而得到垂直平分,根据垂直平分线的性质证得,即可;
取格点、,连接交于,连接,根据网格特点,可证明,即,根据相似三角形的判定与性质证明∽得到,然后根据平行线的判定可得到.
本题考查作图应用与设计作图,掌握正方形性质、全等三角形、旋转、锐角三角函数、角平分线、三角形的外角、等腰三角形、线段垂直平分线的性质、三角形内角和定理、相似三角形的判定与性质、平行线、平行线分线段成比例等知识是解题的关键.
21.【答案】解:;;
,;或
或;
在抛物线上的段上任取一点,过点作轴交线段于点,
则线段表示两个水池面积差,
设,则,
,
,
当时,有最大值为.
在范围内,两个水池面积差的最大值为,此时的值为;
水池与水池的面积相等,
,
即:,
.
若水池与水池的面积相等时,有唯一值,
,
解得:.
若水池与水池的面积相等时,有唯一值,的值为.
【解析】
【分析】
本题考查一次函数与二次函数综合,涉及一次函数图象上点的坐标的特征,二次函数图象的性质,二次函数图象上点的坐标的特征.
依据函数图象和函数解析式,利用二次函数的性质解答即可;
利用图象交点的数学意义解答即可;
依据图象,利用数形结合法解答即可;
在范围内,求得两个水池面积差的解析式,利用二次函数性质解答即可;
令,得到关于的一元二次方程,解的方程即可求得值.
【解答】
解:,
又,
抛物线的开口方向向下,当时,水池的面积随长度的增加而减小,
,
当时,水池的面积随长度的增加而减小,水池面积的最大值是.
由图象可知:两函数图象相交于点,,此时两函数的函数值相等,即:
,
解得:或,
表示两个水池面积相等的点是:,,此时的值是:或.
由图象知:图象中点的左侧部分和点的右侧部分,一次函数的函数值大于二次函数的函数值,
即当或时,水池的面积大于水池的面积,
见答案;
见答案.
22.【答案】
【解析】解:【问题一】正方形的对角线相交于点,
,,,
四边形是正方形,
,
,
≌,
,
故答案为:;
【问题二】如图,
连接,,
点是正方形的中心,
,
点是正方形的中心,
,,,
,
,
,
≌,
,
;
【问题三】在直线上存在点,使为直角三角形,
当时,如图,延长,相交于点,
四边形和四边形是正方形,
,,
四边形是矩形,
,,,
,
,
,
∽,
,
,
,
,
;
当时,如图,
同的方法得,∽,
,
,
,
或;
当时,如图,
过点作的平行线交的延长线于,延长,相交于,
同的方法得,四边形是矩形,
,,,
同的方法得,四边形是矩形,
,,
,
同的方法得,∽,
,
,
,
,
即的长度为或或或.
【问题一】利用判断出≌,即可得出答案;
先求出,再利用判断出≌,即可求出答案;
【问题三】分三种情况:利用三垂线构造出相似三角形,得出比例式求解,即可求出答案.
此题是几何变换综合题,主要考查了正方形的性质,矩形的判定和性质,全等三角形的判定和性质,相似三角形的判定和性质,作出辅助线构造出相似三角形和全等三角形是解本题的关键.
23.【答案】解:;顶点.
过点作轴于点,
,,
,
,
,
当点在线段的右侧时,轴,如图,
;
当点在线段左侧时,设直线与轴交于点,则是等腰三角形,
,
设,则,,
在中,,
解得,
,
直线的解析式为:,
令,则,
解得:,
.
综上,点的坐标为或;
点与点关于对称轴对称,
.
如图,分别过点,作轴的平行线,交直线于点,,
直线的解析式是,
,,
点横坐标为,
,,
.
,,
,
,
当时,的最大值为.
【解析】令,求出的值即可得出点的坐标,将函数化作顶点式可得出点的坐标;
过点作轴于点,易得,因为,所以,分两种情况进行讨论,当点在线段的右侧时,轴,当点在线段左侧时,设直线与轴交于点,则是等腰三角形,分别求出点的坐标即可;
分别过点,作轴的平行线,交直线于点,,则,,由点的横坐标为,可表达,再利用二次函数的性质可得出结论.
令,
解得或,
;
,
顶点.
本题属于二次函数综合题,主要考查二次函数的性质,二次函数上的坐标特征,三角形的面积,解题的关键正确表达两个三角形面积的比.
第1页,共1页
一、选择题(本大题共9小题,共27.0分。在每小题列出的选项中,选出符合题目的一项)
1. 下列说法正确的是( )
A. 为了解我国中小学生的睡眠情况,应采取全面调查的方式
B. 一组数据,,,,,,的众数和平均数都是
C. 若甲、乙两组数据的方差分别是,,则甲组数据比乙组数据更稳定
D. 抛掷一枚硬币次,一定有次“正面向上”
2. 下列图形中,既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
3. 下列计算正确的是( )
A. B. C. D.
4. 由个大小相同的小正方体搭成的几何体如图所示,它的主视图是( )
A.
B.
C.
D.
5. 在反比例函数的图象的每一支上,都随的增大而减小,且整式是一个完全平方式,则该反比例函数的解析式为( )
A. B. C. D.
6. 小王同学从家出发,步行到离家米的公园晨练,分钟后爸爸也从家出发沿着同一路线骑自行车到公园晨练,爸爸到达公园后立即以原速折返回到家中,两人离家的距离单位:米与出发时间单位:分钟的函数关系如图所示,则两人先后两次相遇的时间间隔为( )
A. 分钟 B. 分钟 C. 分钟 D. 分钟
7. 随着信息化的发展,二维码已经走进我们的日常生活,其图案主要由黑、白两种小正方形组成.现对由三个小正方形组成的“”进行涂色,每个小正方形随机涂成黑色或白色,恰好是两个黑色小正方形和一个白色小正方形的概率为( )
A. B. C. D.
8. 在一节数学实践活动课上,老师拿出三个边长都为的正方形硬纸板,他向同学们提出了这样一个问题:若将三个正方形纸板不重叠地放在桌面上,用一个圆形硬纸板将其盖住,这样的圆形硬纸板的最小直径为单位:( )
A. B. C. D.
9. 方程的实数根就是方程的实数根,用“数形结合”思想判定方程的根的情况,正确的是( )
A. 方程有个不等实数根 B. 方程的实数根满足
C. 方程的实数根满足 D. 方程的实数根满足
二、填空题(本大题共6小题,共18.0分)
10. 计算的结果是 .
11. 开学前,根据学校防疫要求,小宁同学连续天进行了体温测量,结果统计如下表:
体温
天数天
这天中,小宁体温的中位数为 .
12. 方程的解是 .
13. 如图,有甲乙两座建筑物,从甲建筑物点处测得乙建筑物点的俯角为,点的俯角为,为两座建筑物的水平距离.已知乙建筑物的高度为,则甲建筑物的高度为______
,结果保留整数.
14. 已知二次函数的部分图象如图所示,对称轴为直线,有以下结论:;若为任意实数,则有;当图象经过点时,方程的两根为,,则,其中,其中正确的是 填写序号.
15. 如图,中,,是外面的一点,连接,,且,,,则的长为 .
三、解答题(本大题共8小题,共72.0分。解答应写出文字说明,证明过程或演算步骤)
16. 本小题分
解不等式组请按下列步骤完成解答.
解不等式,得______;
解不等式,得______;
把不等式和的解集在数轴上表示出来;
原不等式组的解集是______.
17. 本小题分
如图,平行四边形中,点、在对角线上,且求证:
≌;
四边形是平行四边形.
18. 本小题分
为落实“双减”政策,优化作业管理,某中学从全体学生中随机抽取部分学生,调查他们每天完成书面作业的时间单位:分钟按照完成时间分成五组:组“”,组“”,组“”,组“”,组“”将收集的数据整理后,绘制成如下两幅不完整的统计图.
根据以上信息,解答下列问题:
这次调查的样本容量是______,请补全条形统计图;
在扇形统计图中,组的圆心角是______度,本次调查数据的中位数落在______组内;
若该校有名学生,请你估计该校每天完成书面作业不超过分钟的学生人数.
19. 本小题分
如图是直径,是上异于,的一点,点是延长线上一点,连、、,且.
求证:直线是的切线;
若,作的平分线交于,交于,连接、,若,求的值.
20. 本小题分
在如图所示的网格中仅用无刻度的直尺完成画图,画图过程用虚线表示,画图结果用实线表示,按要求完成下列问题:
画格点,使;
画的高;
将线段绕点逆时针旋转得到线段,画出线段;
在上找一点,使.
21. 本小题分
【生活情境】
为美化校园环境,某学校根据地形情况,要对景观带中一个长,宽的长方形水池进行加长改造如图,改造后的水池仍为长方形,以下简称水池同时,再建造一个周长为的矩形水池如图,以下简称水池.
【建立模型】
如果设水池的边加长长度为,加长后水池的总面积为,则关于的函数解析式为:;设水池的边的长为,面积为,则关于的函数解析式为:,上述两个函数在同一平面直角坐标系中的图像如图.
【问题解决】
若水池的面积随长度的增加而减小,则长度的取值范围是______可省略单位,水池面积的最大值是______;
在图字母标注的点中,表示两个水池面积相等的点是______,此时的值是______;
当水池的面积大于水池的面积时,的取值范围是______;
在范围内,求两个水池面积差的最大值和此时的值;
假设水池的边的长度为,其他条件不变这个加长改造后的新水池简称水池,则水池的总面积关于的函数解析式为:若水池与水池的面积相等时,有唯一值,求的值.
22. 本小题分
同学们还记得吗?图,图是人教版八年级下册教材“实验与探究”中我们研究过的两个图形.受这两个图形的启发,数学兴趣小组提出了以下三个问题,请你回答:
【问题一】如图,正方形的对角线相交于点,点又是正方形的一个顶点,交于点,交于点,则与的数量关系为______;
【问题二】受图启发,兴趣小组画出了图:直线、经过正方形的对称中心,直线分别与、交于点、,直线分别与、交于点、,且,若正方形边长为,求四边形的面积;
【问题三】受图启发,兴趣小组画出了图:正方形的顶点在正方形的边上,顶点在的延长线上,且,在直线上是否存在点,使为直角三角形?若存在,求出的长度;若不存在,说明理由.
23. 本小题分
抛物线与直线交于原点和点,与轴交于另一点,顶点为.
直接写出点和点的坐标;
如图,连接,为轴上的动点,当时,求点的坐标;
如图,是点关于抛物线对称轴的对称点,是抛物线上的动点,它的横坐标为,连接,,与直线交于点设和的面积分别为和,求的最大值.
答案和解析
1.【答案】
【解析】解:为了解我国中小学生的睡眠情况,应采取抽样调查的方式,故本选项不合题意;
B.数据,,,,,,的众数是平均数为,故本选项不合题意;
C.若甲、乙两组数据的方差分别是,,则甲组数据比乙组数据更稳定,说法正确,故本选项符合题意;
D.抛掷一枚硬币次,不一定有次“正面向上”,故本选项不合题意;
故选:.
选项A根据抽样调查和全面调查的意义判断即可;选项B根据众数和平均数的定义判断即可;选项C根据方差的意义判断即可;选项D根据随机事件的定义判断即可.
本题考查了方差,众数,平均数以及全面调查与抽样调查,掌握相关定义是解答本题的关键.
2.【答案】
【解析】解:、该字母不是中心对称图形,是轴对称图形,故此选项不合题意;
B、该字母不是中心对称图形,是轴对称图形,故此选项不合题意;
C、该字母是中心对称图形,不是轴对称图形,故此选项不合题意;
D、该字母既是轴对称图形又是中心对称图形,故此选项符合题意;
故选:.
根据中心对称图形与轴对称图形的概念进行判断即可.
本题考查的是中心对称图形与轴对称图形的概念.轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合,中心对称图形是要寻找对称中心,旋转度后与自身重合.
3.【答案】
【解析】解:,故A错误,不符合题意;
,故B错误,不符合题意;
,故C正确,符合题意;
,故D错误,不符合题意;
故选:.
根据同底数幂的乘除、幂的乘方与积的乘方、合并同类项法则逐项判断.
本题考查整式的运算,解题的关键是掌握整式运算的相关法则.
4.【答案】
【解析】解:从正面看,底层是三个小正方形,上层的左边是一个小正方形,
故选:.
根据从正面看得到的图形是主视图,可得答案.
本题考查了简单组合体的三视图.解题的关键是理解简单组合体的三视图的定义,明确从正面看得到的图形是主视图.
5.【答案】
【解析】解:在反比例函数的图象的每一支上,都随的增大而减小,
,则,
整式是一个完全平方式,
,则,
,
该反比例函数的解析式为,
故选:.
先根据反比例函数的性质得到,再根据完全平方式的特点求得,进而求得即可求解.
本题考查反比例函数的图象与性质、完全平方式,熟知完全平方式的结构是解答的关键.
6.【答案】
【解析】解:由图象可得,
小明的速度为米分钟,
爸爸的速度为:米分钟,
设小明出发分钟两人第一次相遇,出发分钟两人第二次相遇,
,,
解得,,
,
故选:.
根据题意和函数图象中的数据,可以先表示出两人的速度,然后即可计算出两人第一次和第二次相遇的时间,然后作差即可.
本题考查一次函数的应用,解答本题的关键是明确题意,求出两人相遇的时间.
7.【答案】
【解析】解:画树状图如下:
由树状图知,共有种等可能结果,其中恰好是两个黑色小正方形和一个白色小正方形的有种结果,
所以恰好是两个黑色小正方形和一个白色小正方形的概率为,
故选:.
画树状图得出所有等可能结果,从中找到符合条件的结果数,再根据概率公式求解即可.
本题主要考查列表法与树状图法求概率,列举法树状图法求概率的关键在于列举出所有可能的结果,列表法是一种,但当一个事件涉及三个或更多元素时,为不重不漏地列出所有可能的结果,通常采用树状图.
8.【答案】
【解析】解:如图所示:设圆心为,与交点为,连接、、,
垂直平分,,
在上,,
设,则,
在中,
在中,
解得:,
则,
圆形硬纸板的最小直径为,
故选:.
连接、、,设,根据勾股定理列出关于的方程,解方程得到答案.
本题考查的是正多边形和圆的有关计算,掌握正方形的性质、勾股定理、垂径定理是解题的关键.
9.【答案】
【解析】解:方程的实数根就是方程的实数根,
方程的根可以看作是:与两函数的交点的横坐标,
函数和函数的图象如图,
观察图象,函数和函数的图象有一个交点,交点的横坐标在范围内,
所以,方程的实数根满足.
故选:.
画出函数和函数的图象,观察交点情况,即可判断方程的根的情况.
本题考查的是反比例函数及二次函数的图象,根据判别式及高次方程,利用数形结合求解是解题的关键.
10.【答案】
【解析】解:,
故答案为:.
根据二次根式的性质求解即可.
本题考查二次根式的性质,熟练掌握二次根式的性质是解答的关键,注意符号问题.
11.【答案】
【解析】解:在所给个数据中,第和第个的数据均为,
小宁体温的中位数为,
故答案为:.
根据中位数的定义求第和第个的数据的平均数即可.
本题考查中位数,解答关键是熟知中位数是一组数据从小到大或从大到小重新排列后,若数据是奇数个,则中位数是最中间的那个数,如果数据是偶数个,则中位数是最中间两个数的平均数,注意先进行排序.
12.【答案】
【解析】
【分析】
此题考查了解分式方程,利用了转化的思想,解分式方程时注意要检验.
分式方程去分母转化为整式方程,求出整式方程的解得到的值,经检验即可得到分式方程的解.
【解答】
解:去分母得:,
解得:,
经检验是分式方程的解.
故答案为:.
13.【答案】
【解析】解:过点作于点,如图.
则,,,
在中,,
设,则,
,,
在中,
,
解得,
.
故答案为:.
过点作于点,则,,,在中,,设,则,,,在中,,解得,进而可得出答案.
本题考查解直角三角形的应用仰角俯角问题,熟练掌握锐角三角函数的定义是解答本题的关键.
14.【答案】
【解析】解:抛物线的开口向上,与轴负半轴相交,
,,
抛物线的对称轴为直线,
,
,
,
故正确;
当时,有最小值,
为任意实数,
即,
故正确;
图象经过点,对称轴为直线,
二次函数图象经过另一个点,
即二次函数与直线的交点为和,
方程的两个根为,,
,
故正确,
综上,正确的是,
故答案为:.
根据抛物线的开口方向和对称轴方程、与轴的交点可判断;利用时取得最小值可判断;由抛物线与直线的交点以及抛物线的对称性可判断,进而可得结论.
本题考查二次函数图象与系数的关系,掌握二次函数的性质,数形结合思想求解是解答的关键.
15.【答案】
【解析】解:作于点,交于点,连接,
,
,
,即,
设,,则,,,,
,即,
∽,
,,
,,
即,
在中,,即,
解得,
.
故答案为:.
作于点,交于点,连接,由,设,,则,,,,推出∽,求得,,在中,利用勾股定理即可求解.
本题考查了解直角三角形,相似三角形的判定和性质,勾股定理等,作出辅助线,证明∽是解题的关键.
16.【答案】解:;
;
如图所示:
.
【解析】解:解不等式,得:;
解不等式,得:;
把不等式和的解集在数轴上表示出来为:
原不等式组的解集为:.
故答案为:;
;
.
分别解这两个不等式,把不等式和的解集在数轴上表示出来,找到解集的公共部分即可得到原不等式组的解集.
本题考查了解一元一次不等式组,在数轴上表示不等式的解集,体现了数形结合的思想,在数轴上找到解集的公共部分是解题的关键.
17.【答案】证明四边形是平行四边形,
,
,
,
≌ ;
证明:由知,≌,
,,
,
,
四边形是平行四边形.
【解析】根据平行四边形平行四边形的性质得到 ,从而得到,然后利用证得两三角形全等即可;
利用中的全等三角形的对应角相等推知,则等角的补角相等,即,所以根据“有一组对边平行且相等”证得结论.
本题考查了全等三角形的判定与性质,平行四边形的判定与性质.平行四边形的判定方法共有五种,应用时要认真领会它们之间的联系与区别,同时要根据条件合理、灵活地选择方法.
18.【答案】,
补全的条形统计图如图所示:
;;
人,
答:估计该校每天完成书面作业不超过分钟的学生有人.
【解析】解:这次调查的样本容量是:,
组的人数为:人,
故答案为:;
在扇形统计图中,组的圆心角是:,
本次调查了个数据,第个数据和个数据都在组,
中位数落在组,
故答案为:;;
见答案.
根据组的人数和所占的百分比,可以计算出本次调查的人数,然后即可计算出组的人数,从而可以将条形统计图补充完整;
根据统计图中的数据,可以计算出组的圆心角的度数,以及中位数落在哪一组;
根据题意和统计图中的数据,可以计算出该校每天完成书面作业不超过分钟的学生人数.
本题考查条形统计图、扇形统计图、用样本估计总体、中位数,解答本题的关键是明确题意,利用数形结合的思想解答.
19.【答案】证明:连接,
是直径,
,则,
,
,
又,
,即,
是半径,
直线是的切线;
解:设,
,
,,
在中,,,
,解得或舍去,
,,
∽,
,则,
在中,,
,,
平分,
,
又,
∽,
,
.
【解析】连接,先利用圆周角定理得到,再根据等腰三角形的性质结合已知可证得,然后根据切线的判定可证得结论;
设,根据勾股定理求出,再证明∽,然后利用相似三角形的性质得到,再次利用勾股定理求得,,证明∽,得到求解即可.
本题考查圆周角定理、切线的判定、等腰三角形的性质、相似三角形的判定与性质、勾股定理、角平分线的定义等知识,熟练掌握相关知识的联系与运用,会利用相似三角形的性质求解是解答的关键.
20.【答案】解:方法一:如图,取格点,连接,则,
,
,
故点即为所求作;
方法二:还可取格点,连接,,则,
,
根据网格特点和全等三角形的性质得,
,
故点即为所求作;
取格点,连接交于,
则即为所求作的高;
理由:由网格特点,,
则,
,与相交,
,
即;
取格点、,连接交于,连接,则线段即为所求作;
理由:根据网格特点,,则,
,
,则,又,
垂直平分,
,即;
取格点、,连接交于,连接,则,故点即为所求.
理由:根据网格特点,,
即,又,
∽,
,
.
【解析】取格点,连接,则,根据等腰三角形的性质和三角形的外角性质可求解;还可取格点,连接,,则,,再根据网格特点和全等三角形的性质得到平分,进而可得到;
取格点,连接交于,由网格特点,证明,根据三角形的内角和定理和对顶角相等证得即可;
取格点、,连接交于,连接,根据网格特点,证明得到,根据平行线分线段成比例可得,进而得到垂直平分,根据垂直平分线的性质证得,即可;
取格点、,连接交于,连接,根据网格特点,可证明,即,根据相似三角形的判定与性质证明∽得到,然后根据平行线的判定可得到.
本题考查作图应用与设计作图,掌握正方形性质、全等三角形、旋转、锐角三角函数、角平分线、三角形的外角、等腰三角形、线段垂直平分线的性质、三角形内角和定理、相似三角形的判定与性质、平行线、平行线分线段成比例等知识是解题的关键.
21.【答案】解:;;
,;或
或;
在抛物线上的段上任取一点,过点作轴交线段于点,
则线段表示两个水池面积差,
设,则,
,
,
当时,有最大值为.
在范围内,两个水池面积差的最大值为,此时的值为;
水池与水池的面积相等,
,
即:,
.
若水池与水池的面积相等时,有唯一值,
,
解得:.
若水池与水池的面积相等时,有唯一值,的值为.
【解析】
【分析】
本题考查一次函数与二次函数综合,涉及一次函数图象上点的坐标的特征,二次函数图象的性质,二次函数图象上点的坐标的特征.
依据函数图象和函数解析式,利用二次函数的性质解答即可;
利用图象交点的数学意义解答即可;
依据图象,利用数形结合法解答即可;
在范围内,求得两个水池面积差的解析式,利用二次函数性质解答即可;
令,得到关于的一元二次方程,解的方程即可求得值.
【解答】
解:,
又,
抛物线的开口方向向下,当时,水池的面积随长度的增加而减小,
,
当时,水池的面积随长度的增加而减小,水池面积的最大值是.
由图象可知:两函数图象相交于点,,此时两函数的函数值相等,即:
,
解得:或,
表示两个水池面积相等的点是:,,此时的值是:或.
由图象知:图象中点的左侧部分和点的右侧部分,一次函数的函数值大于二次函数的函数值,
即当或时,水池的面积大于水池的面积,
见答案;
见答案.
22.【答案】
【解析】解:【问题一】正方形的对角线相交于点,
,,,
四边形是正方形,
,
,
≌,
,
故答案为:;
【问题二】如图,
连接,,
点是正方形的中心,
,
点是正方形的中心,
,,,
,
,
,
≌,
,
;
【问题三】在直线上存在点,使为直角三角形,
当时,如图,延长,相交于点,
四边形和四边形是正方形,
,,
四边形是矩形,
,,,
,
,
,
∽,
,
,
,
,
;
当时,如图,
同的方法得,∽,
,
,
,
或;
当时,如图,
过点作的平行线交的延长线于,延长,相交于,
同的方法得,四边形是矩形,
,,,
同的方法得,四边形是矩形,
,,
,
同的方法得,∽,
,
,
,
,
即的长度为或或或.
【问题一】利用判断出≌,即可得出答案;
先求出,再利用判断出≌,即可求出答案;
【问题三】分三种情况:利用三垂线构造出相似三角形,得出比例式求解,即可求出答案.
此题是几何变换综合题,主要考查了正方形的性质,矩形的判定和性质,全等三角形的判定和性质,相似三角形的判定和性质,作出辅助线构造出相似三角形和全等三角形是解本题的关键.
23.【答案】解:;顶点.
过点作轴于点,
,,
,
,
,
当点在线段的右侧时,轴,如图,
;
当点在线段左侧时,设直线与轴交于点,则是等腰三角形,
,
设,则,,
在中,,
解得,
,
直线的解析式为:,
令,则,
解得:,
.
综上,点的坐标为或;
点与点关于对称轴对称,
.
如图,分别过点,作轴的平行线,交直线于点,,
直线的解析式是,
,,
点横坐标为,
,,
.
,,
,
,
当时,的最大值为.
【解析】令,求出的值即可得出点的坐标,将函数化作顶点式可得出点的坐标;
过点作轴于点,易得,因为,所以,分两种情况进行讨论,当点在线段的右侧时,轴,当点在线段左侧时,设直线与轴交于点,则是等腰三角形,分别求出点的坐标即可;
分别过点,作轴的平行线,交直线于点,,则,,由点的横坐标为,可表达,再利用二次函数的性质可得出结论.
令,
解得或,
;
,
顶点.
本题属于二次函数综合题,主要考查二次函数的性质,二次函数上的坐标特征,三角形的面积,解题的关键正确表达两个三角形面积的比.
第1页,共1页
同课章节目录
