人教版 八年级下册 第十八章18.1.2平行四边形的判定课后练习 (含答案)
文档属性
| 名称 | 人教版 八年级下册 第十八章18.1.2平行四边形的判定课后练习 (含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 359.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-13 00:00:00 | ||
图片预览


文档简介
18.1.2平行四边形的判定
一、单选题
1.顺次连结任意四边形各边中点所得的四边形必定是( )
A.任意四边形 B.平行四边形 C.菱形 D.矩形
2.在四边形ABCD中,对角线AC、BD相交于点O,下列条件中不一定能判定这个四边形是平行四边形的是( ).
A.AB∥DC,AD=BC B.∠BAD=∠BCD,∠ABC=∠ADC
C.OA=OC,OB=OD D.AB=DC,AD=BC
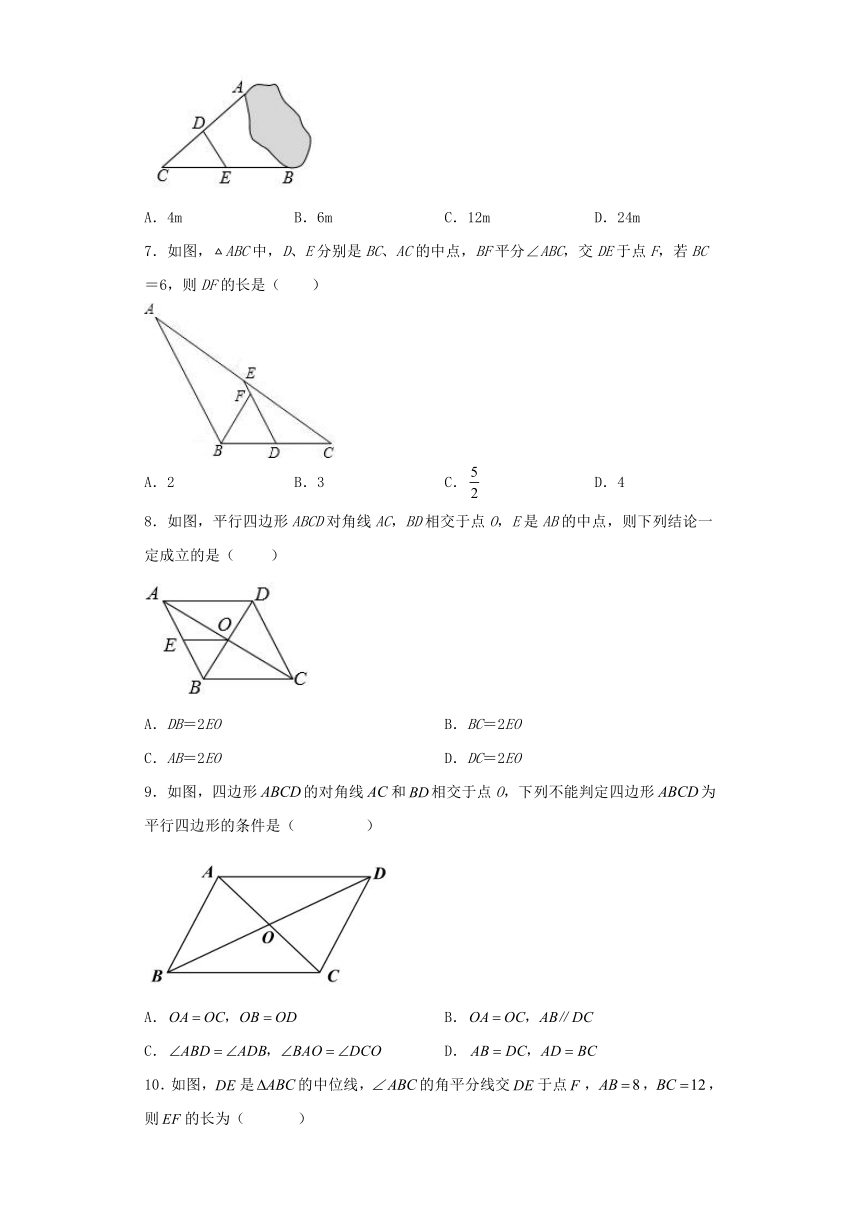
3.如图,AD为△ABC中∠ BAC的外角平分线,BD⊥AD于D,E为BC中点,DE=5,AC=3,则AB长为()
A.8.5 B.8 C.7.5 D.7
4.小军不慎将一块平行四边形玻璃打碎成如图所示的四块,他带了两块碎玻璃到商店配成一块与原来相同的平行四边形玻璃,他带的碎玻璃编号是( )
A.①② B.①④ C.②③ D.②④
5.如图,为了测量池塘边A、B两地之间的距离,在的同侧取一点C,连接并延长至点D,连接并延长至点E,使得点A、B分别是的中点,若测得,则A、B间的距离是( )
A. B. C. D.
6.如图,为了测量位于一水潭旁的两点A,B的距离,在AB外选了一点C,分别取AC、BC的中点D、E,量得,则A、B间的距离为( )
A.4m B.6m C.12m D.24m
7.如图,ABC中,D、E分别是BC、AC的中点,BF平分∠ABC,交DE于点F,若BC=6,则DF的长是( )
A.2 B.3 C. D.4
8.如图,平行四边形ABCD对角线AC,BD相交于点O,E是AB的中点,则下列结论一定成立的是( )
A.DB=2EO B.BC=2EO
C.AB=2EO D.DC=2EO
9.如图,四边形的对角线和相交于点O,下列不能判定四边形为平行四边形的条件是( )
A. B.
C. D.
10.如图,是的中位线,的角平分线交于点,,,则的长为( )
A.1 B.1.5 C.2 D.2.5
二、填空题
11.已知四边形,点是对角线与的交点,且,请再添加一个条件,使得四边形成为平行四边形,那么添加的条件可以是_____________.(用数学符号语言表达)
12.三角形的各边分别为8cm 、10cm和12cm ,连结各边中点所成三角形的周长=_____
13.在四边形ABCD中,BD是对角线,∠ABD=∠CDB,要使四边形ABCD是平行四边形只需添加一个条件,这个条件可以是_________(只需写出一种情况).
14.中,已知AB=CD=4,BC=6,则当AD=________时,四边形ABCD是平行四边形.
15.平行四边形的两个顶点的坐标分别是(﹣3,0),(1,0),第3个顶点在y轴的正半轴上,且与x轴的距离为3个单位长度,则第4个顶点的坐标是_____.
三、解答题
16.如图,在中,,点 , 分别是 , 的中点,延长 至点 ,使,连接 、 、 ,求证:四边形 是平行四边形.
17.如图,AC是平行四边形ABCD的一条对角线,DE⊥AC,BF⊥AC垂足分别是E、F.
求证:四边形DEBF是平行四边形.
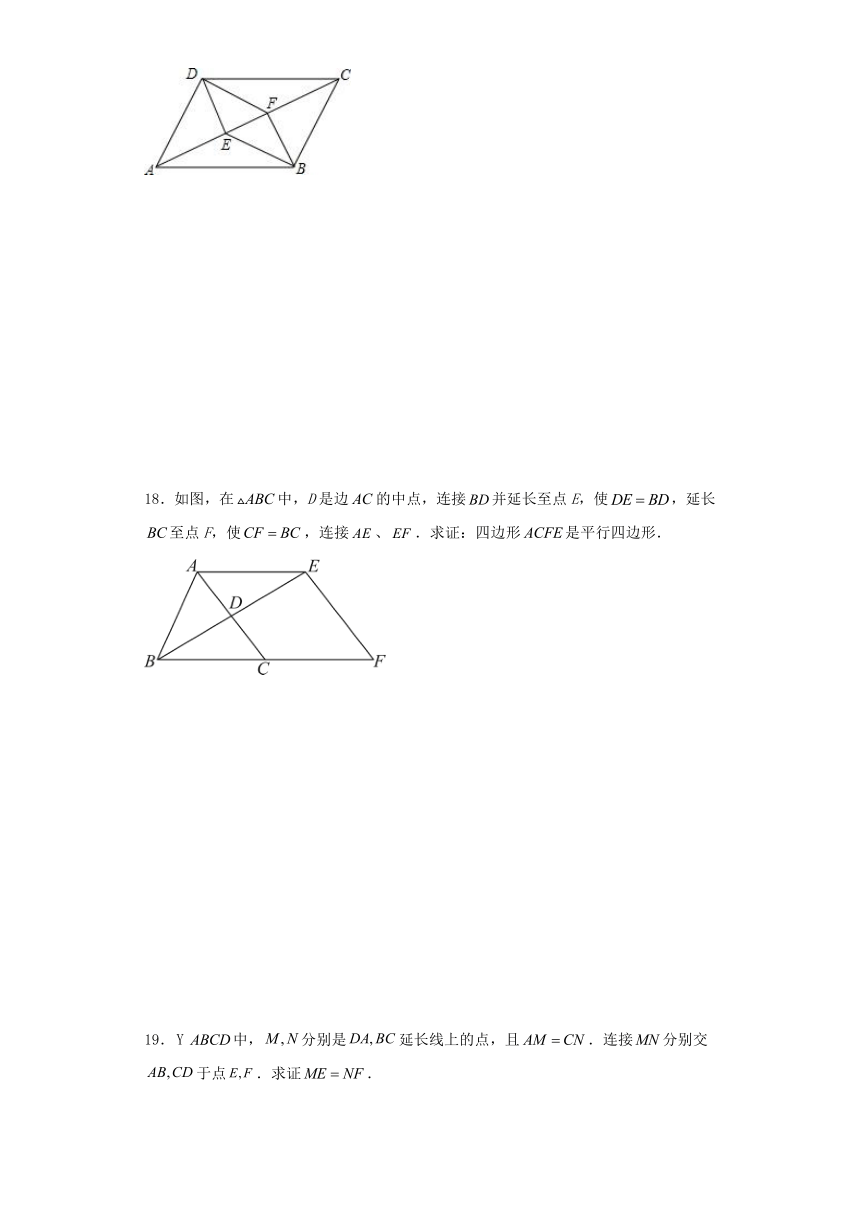
18.如图,在中,D是边的中点,连接并延长至点E,使,延长至点F,使,连接、.求证:四边形是平行四边形.
19.中,分别是延长线上的点,且.连接分别交于点.求证.
20.如图,在△ABC中,AB=AC,AE是∠BAC的角平分线,点O为AB的中点,延长EO交△ABC的外角平分线于点F.
(1)求证:EO=AB;
(2)试判断四边形ACEF的形状,并证明你的结论.
参考答案
1.B
2.A
3.D
4.C
5.C
6.D
7.B
8.B
9.C
10.C
11.
12.15 cm
13.AB=CD(答案不唯一)
14.6
15.(﹣4,3)或(﹣2,﹣3)或1(4,3).
16.证明:∵在 中点 , 分别是边 , 的中点,
∴ 是的中位线,即,,
∵, , , 共线,
∴,.
故四边形 是平行四边形.
17.解:∵AC是平行四边形ABCD的一条对角线,
∴ , ,
∴ ,
∵DE⊥AC,BF⊥AC,
∴ , ,
在 和 中,
∵ ,
∴ ,
∴ ,
∵ ,
∴四边形DEBF是平行四边形.
18.证明:如图,连接,
是边的中点,
,
,
四边形是平行四边形,
,,
,
,
,
四边形是平行四边形.
19.证明:是平行四边形,.
,
,
,
,
.
20.解:证明:(1)∵AB=AC,AE是∠BAC的平分线,
∴BE=EC,
∵点O为AB的中点,
∴OB=OA,
∴EO是△ABC的中位线,
∴EO=AB;
(2)四边形ACEF是平行四边形.
∵EO是△ABC的中位线,
∴EO//AC,
∵AB=AC,
∴∠B=∠C,
∵AF是∠BAD的平分线,
∴∠BAD=2∠BAF,
∵∠BAD=∠B+∠C=2∠B
∴∠B=∠BAF,
∴AF//BC,
∴四边形ACEF是平行四边形.
一、单选题
1.顺次连结任意四边形各边中点所得的四边形必定是( )
A.任意四边形 B.平行四边形 C.菱形 D.矩形
2.在四边形ABCD中,对角线AC、BD相交于点O,下列条件中不一定能判定这个四边形是平行四边形的是( ).
A.AB∥DC,AD=BC B.∠BAD=∠BCD,∠ABC=∠ADC
C.OA=OC,OB=OD D.AB=DC,AD=BC
3.如图,AD为△ABC中∠ BAC的外角平分线,BD⊥AD于D,E为BC中点,DE=5,AC=3,则AB长为()
A.8.5 B.8 C.7.5 D.7
4.小军不慎将一块平行四边形玻璃打碎成如图所示的四块,他带了两块碎玻璃到商店配成一块与原来相同的平行四边形玻璃,他带的碎玻璃编号是( )
A.①② B.①④ C.②③ D.②④
5.如图,为了测量池塘边A、B两地之间的距离,在的同侧取一点C,连接并延长至点D,连接并延长至点E,使得点A、B分别是的中点,若测得,则A、B间的距离是( )
A. B. C. D.
6.如图,为了测量位于一水潭旁的两点A,B的距离,在AB外选了一点C,分别取AC、BC的中点D、E,量得,则A、B间的距离为( )
A.4m B.6m C.12m D.24m
7.如图,ABC中,D、E分别是BC、AC的中点,BF平分∠ABC,交DE于点F,若BC=6,则DF的长是( )
A.2 B.3 C. D.4
8.如图,平行四边形ABCD对角线AC,BD相交于点O,E是AB的中点,则下列结论一定成立的是( )
A.DB=2EO B.BC=2EO
C.AB=2EO D.DC=2EO
9.如图,四边形的对角线和相交于点O,下列不能判定四边形为平行四边形的条件是( )
A. B.
C. D.
10.如图,是的中位线,的角平分线交于点,,,则的长为( )
A.1 B.1.5 C.2 D.2.5
二、填空题
11.已知四边形,点是对角线与的交点,且,请再添加一个条件,使得四边形成为平行四边形,那么添加的条件可以是_____________.(用数学符号语言表达)
12.三角形的各边分别为8cm 、10cm和12cm ,连结各边中点所成三角形的周长=_____
13.在四边形ABCD中,BD是对角线,∠ABD=∠CDB,要使四边形ABCD是平行四边形只需添加一个条件,这个条件可以是_________(只需写出一种情况).
14.中,已知AB=CD=4,BC=6,则当AD=________时,四边形ABCD是平行四边形.
15.平行四边形的两个顶点的坐标分别是(﹣3,0),(1,0),第3个顶点在y轴的正半轴上,且与x轴的距离为3个单位长度,则第4个顶点的坐标是_____.
三、解答题
16.如图,在中,,点 , 分别是 , 的中点,延长 至点 ,使,连接 、 、 ,求证:四边形 是平行四边形.
17.如图,AC是平行四边形ABCD的一条对角线,DE⊥AC,BF⊥AC垂足分别是E、F.
求证:四边形DEBF是平行四边形.
18.如图,在中,D是边的中点,连接并延长至点E,使,延长至点F,使,连接、.求证:四边形是平行四边形.
19.中,分别是延长线上的点,且.连接分别交于点.求证.
20.如图,在△ABC中,AB=AC,AE是∠BAC的角平分线,点O为AB的中点,延长EO交△ABC的外角平分线于点F.
(1)求证:EO=AB;
(2)试判断四边形ACEF的形状,并证明你的结论.
参考答案
1.B
2.A
3.D
4.C
5.C
6.D
7.B
8.B
9.C
10.C
11.
12.15 cm
13.AB=CD(答案不唯一)
14.6
15.(﹣4,3)或(﹣2,﹣3)或1(4,3).
16.证明:∵在 中点 , 分别是边 , 的中点,
∴ 是的中位线,即,,
∵, , , 共线,
∴,.
故四边形 是平行四边形.
17.解:∵AC是平行四边形ABCD的一条对角线,
∴ , ,
∴ ,
∵DE⊥AC,BF⊥AC,
∴ , ,
在 和 中,
∵ ,
∴ ,
∴ ,
∵ ,
∴四边形DEBF是平行四边形.
18.证明:如图,连接,
是边的中点,
,
,
四边形是平行四边形,
,,
,
,
,
四边形是平行四边形.
19.证明:是平行四边形,.
,
,
,
,
.
20.解:证明:(1)∵AB=AC,AE是∠BAC的平分线,
∴BE=EC,
∵点O为AB的中点,
∴OB=OA,
∴EO是△ABC的中位线,
∴EO=AB;
(2)四边形ACEF是平行四边形.
∵EO是△ABC的中位线,
∴EO//AC,
∵AB=AC,
∴∠B=∠C,
∵AF是∠BAD的平分线,
∴∠BAD=2∠BAF,
∵∠BAD=∠B+∠C=2∠B
∴∠B=∠BAF,
∴AF//BC,
∴四边形ACEF是平行四边形.
