18.2.3 正方形 重点易错点知识专项练 2022-2023学年初中数学人教版八年级下册(含答案)
文档属性
| 名称 | 18.2.3 正方形 重点易错点知识专项练 2022-2023学年初中数学人教版八年级下册(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 545.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-13 15:39:46 | ||
图片预览




文档简介
18.2.3 正方形
1.以下四个命题
①两条对角线互相平分的四边形是平行四边形;
②两条对角线相等的四边形是矩形;
③两条对角线互相垂直的平行四边形是菱形;
④有一组邻边相等且有一个角是直角的四边形是正方形,
其中是真命题的是( )
A.①② B.③④ C.①③ D.②④
2.平行四边形、矩形、菱形、正方形都具有的是( )
A.对角线互相平分
B.对角线互相垂直
C.对角线相等
D.对角线互相垂直且相等
3.如图,在边长为6的正方形内作交于点E,交于点F,连接.若,则的长为( )
A.2 B.3 C.4 D.5
4.如图,在矩形中,对角线、交于点,添加下列一个条件,能使矩形成为正方形的是
A. B. C. D.
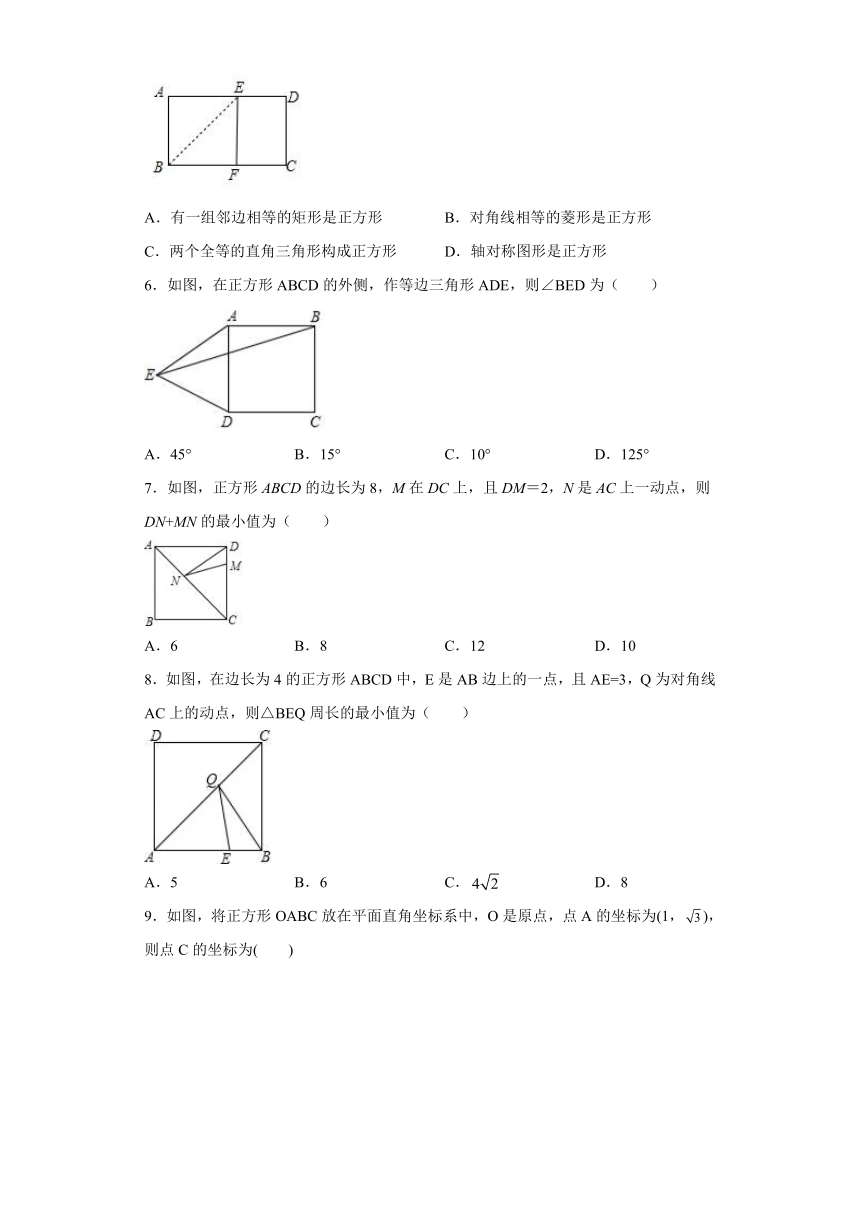
5.如图,将长方形纸片折叠,使点落在边上的处,折痕为,若沿剪下,则折叠部分展开是一个正方形,其数学原理是( )
A.有一组邻边相等的矩形是正方形 B.对角线相等的菱形是正方形
C.两个全等的直角三角形构成正方形 D.轴对称图形是正方形
6.如图,在正方形ABCD的外侧,作等边三角形ADE,则∠BED为( )
A.45° B.15° C.10° D.125°
7.如图,正方形ABCD的边长为8,M在DC上,且DM=2,N是AC上一动点,则DN+MN的最小值为( )
A.6 B.8 C.12 D.10
8.如图,在边长为4的正方形ABCD中,E是AB边上的一点,且AE=3,Q为对角线AC上的动点,则△BEQ周长的最小值为( )
A.5 B.6 C. D.8
9.如图,将正方形OABC放在平面直角坐标系中,O是原点,点A的坐标为(1,),则点C的坐标为( )
A.(-,1) B.(-1,) C.(,1) D.(-,-1)
10.将n个边长都为1cm的正方形按如图所示的方法摆放,点A1,A2,…,An分别是正方形对角线的交点,则n个正方形重叠形成的重叠部分的面积和为( )
A.cm2 B.cm2 C. cm2 D.()ncm2
11.为增加绿化面积,某小区将原来正方形地砖更换为如图所示的正八边形植草砖,更换后,图中阴影部分为植草区域,设正八边形与其内部小正方形的边长都为a,则阴影部分的面积为( )
A.2a2 B.3a2 C.4a2 D.5a2
12.如图,已知方格纸中是4个相同的正方形,则∠1+∠2+∠3的度数为( )
A.90° B.105° C.120° D.135°
13.如图,在正方形ABCD外侧,作等边三角形ADE,AC,BE相交于点F,则∠BFC为( )
A.75° B.60° C.55° D.45°
14.如图,正方形ABCD中,点E是AD边的中点,BD,CE交于点H,BE、AH交于点G,则下列结论:
①∠ABE=∠DCE;②∠AHB=∠EHD;③S△BHE=S△CHD;④AG⊥BE.其中正确的是( )
A.①③ B.①②③④ C.①②③ D.①③④
15.若正方形的对角线长为2 cm,则这个正方形的面积为( )
A.4 B.2 C. D.
16.如图,以正方形的边为边向正方形外作等边,与交于点F,则的度数是( )
A.105° B.120° C.135° D.150°
17.如图,矩形纸片ABCD中,AB=6cm,BC=8cm.现将其沿AE对折,使得点B落在边AD上的点B1处,折痕与边BC交于点E,则CB1的长为( )
A.cm B.cm C.8cm D.10cm
18.如图,在正方形ABCD中,E为DC边上的一点,沿线段BE对折后,若∠ABF比∠EBF大15°,则∠EBF的度数为( )
A.15° B.20° C.25° D.30°
19.如图,正方形的两边在坐标轴上,,,点P为OB上一动点,的最小值是( )
A.8 B.10 C. D.
20.如图,点是中斜边(不与,重合)上一动点,分别作于点,作于点,连接、,若,,当点在斜边上运动时,则的最小值是( )
A.1.5 B.2
C.4.8 D.2.4
21.如图,正方形中,,点E在边上,且.将沿对折至,延长交边于点G,连接、.则下列结论:①;②;③;④,错误的是( )
A.① B.② C.③ D.④
22.如图,已知正方形的面积为平方厘米,厘米,则的长为( )
A. B. C. D.
参考答案:
1.C
解:①两条对角线互相平分的四边形是平行四边形.是真命题;
②两条对角线相等的四边形是矩形,是假命题;
③两条对角线互相垂直的平行四边形是菱形,是真命题;
④有一组邻边相等且有一个角是直角的四边形是正方形,是假命题;
2.A
3.A
解:如图,把绕A逆时针旋转90°得到,
∴,
∴,
∴,
∴G、B、E三点共线,
∴,
∵,
∴,
∴,
∴,
在和中,
,
∴,
∴,
设,
∵,
∴,
则,
∴,
∵,
∴,
解得,,
∴的长为2.
4.B
解:要使矩形成为正方形,可根据正方形的判定定理解答:
(1)有一组邻边相等的矩形是正方形,
(2)对角线互相垂直的矩形是正方形.
添加,能使矩形成为正方形.
5.A
解:∵将长方形纸片折叠,A落在BC上的F处,
∴BA=BF,
∵折痕为BE,沿EF剪下,
∴四边形ABFE为矩形,
∴四边形ABEF为正方形.
故用的判定定理是;邻边相等的矩形是正方形.
6.A
是等边三角形,
,,
四边形是正方形,
,,
,,
,
.
7.D
解:如图,连接BM,
∵点B和点D关于直线AC对称,
∴NB=ND,
则BM就是DN+MN的最小值,
∵正方形ABCD的边长是8,DM=2,
∴CM=6,
∴BM==10,
∴DN+MN的最小值是10.
8.B
解:连接BD,DE,
∵四边形ABCD是正方形,
∴点B与点D关于直线AC对称,
∴DE的长即为BQ+QE的最小值,
∵DE=BQ+QE=
∴△BEQ周长的最小值=DE+BE=5+1=6.
故选B.
9.A
解:如图:过点A作AD⊥x轴于D,过点C作CE⊥x轴于E,
∵∠OAD+∠AOD=∠COE+∠AOD,
∴∠OAD=∠COE,
∵OC=OA,∠ODA=∠OEC=90°,
∴△OAD△OCE全等,
∴OE=AD=,CE=OD=1,
∴点C的坐标为(-,1),
10.B
由题意可得阴影部分面积等于正方形面积的,即是,5个这样的正方形重叠部分(阴影部分)的面积和为×4,n个这样的正方形重叠部分(阴影部分)的面积和为×(n-1)=cm2.
11.A
12.D
观察图形可知, 所在的三角形与3所在的三角形全等,
,
又,
.
13.B
解:∵四边形ABCD是正方形,
∴∠BAD=90°,AB=AD,∠BAF=45°,
∵△ADE是等边三角形,
∴∠DAE=60°,AD=AE,
∴∠BAE=90°+60°=150°,AB=AE,
∴∠ABE=∠AEB=(180° 150°)=15°,
∴∠BFC=∠BAF+∠ABE=45°+15°=60°;
14.B
解:四边形是正方形,是边上的中点,
,,,
,
,
故①正确;
∵四边形ABCD是正方形,
∴AB=BC, ∠ABD=∠CBD,
∵BH=BH,
∴,
,
,
,
故②正确;
,
,
,
即,
故③正确;
四边形是正方形,
,,,
,
,
,
,
,
,
,
故④正确;
15.B
如图,连接BD,
正方形ABCD中,,则BD=AC=2,
正方形的面积为=,
16.B
解:∵四边形ABCD是正方形,等边△CDE,
∴∠BCD =90°,∠ACB=45°,∠DCE=60°,CD=CE= CB,
∴∠CBE=∠CEB.
∵∠BCE=∠BCD+∠DCE=90°+60°=150°,
∴∠CBE=15°.
∵∠ACB=45°,
∴∠AFB=∠ACB+∠CBE=60°.
∴∠AFE=120°.
17.B
解:∵∠AB1E=∠B=90°,∠BAB1=90°,
∴四边形ABEB1为矩形,
又∵AB=AB1,
∴四边形ABEB1为正方形,
∴BE=AB=6cm,
∴EC=BC﹣BE=2cm,
∴CB1=cm.
18.C
解:∵∠EBF是∠CBE折叠形成,
∴∠EBF=∠CBE,
∵∠ABF ∠EBF=15°,∠ABF+∠EBF+∠CBE=90°,
∴∠EBF=25°,
19.C
正方形ABCO,
A、C两点关于OB对称,
连接CD,交OB于,
,
,
当C、P、D三点共线时,取最小值,
,,
,
20.C
解:如图所示:连接,
∵,于点,作于点,
∴四边形是矩形,
∴MN=BP,
∴的最小值就是BP最小,
,
当时,最小,
∴.
21.D
解:∵四边形ABCD为正方形,将沿对折至,
∴AB=AD=AF=CD=6,∠AFG=∠AFE=∠D=90°,
∴∠AFG =90°,
∵AG=AG,∠B=∠AFG=90°,
∴Rt△ABG≌Rt△AFG(HL),
∴BG=FG,
∵,
∴,EC=4,设BG=FG=x,则CG=6-x,
在直角△ECG中,根据勾股定理,得,
解得x=3.
∴BG=3=6-3=CG,①正确;
∵CG=BG,BG=GF,
∴CG=GF,
∴△FGC是等腰三角形,∠GFC=∠GCF.
又∵Rt△ABG≌Rt△AFG;
∴∠AGB=∠AGF,∠AGB+∠AGF=2∠AGB=180°-∠FGC=∠GFC+∠GCF=2∠GFC=2∠GCF,
∴∠AGB=∠AGF=∠GFC=∠GCF,
∴AG∥CF,②正确;
∵, ,
∴,③正确;
∵∠BAG=∠FAG,∠DAE=∠FAE,
又∵∠BAD=90°,
∴∠GAE=45°,
∴∠AGB+∠AED=180°-∠GAE=135°,④错误.
22.D
解:∵正方形的面积为平方厘米,
∴,厘米,
在中,
∵厘米,
∴(厘米),
1.以下四个命题
①两条对角线互相平分的四边形是平行四边形;
②两条对角线相等的四边形是矩形;
③两条对角线互相垂直的平行四边形是菱形;
④有一组邻边相等且有一个角是直角的四边形是正方形,
其中是真命题的是( )
A.①② B.③④ C.①③ D.②④
2.平行四边形、矩形、菱形、正方形都具有的是( )
A.对角线互相平分
B.对角线互相垂直
C.对角线相等
D.对角线互相垂直且相等
3.如图,在边长为6的正方形内作交于点E,交于点F,连接.若,则的长为( )
A.2 B.3 C.4 D.5
4.如图,在矩形中,对角线、交于点,添加下列一个条件,能使矩形成为正方形的是
A. B. C. D.
5.如图,将长方形纸片折叠,使点落在边上的处,折痕为,若沿剪下,则折叠部分展开是一个正方形,其数学原理是( )
A.有一组邻边相等的矩形是正方形 B.对角线相等的菱形是正方形
C.两个全等的直角三角形构成正方形 D.轴对称图形是正方形
6.如图,在正方形ABCD的外侧,作等边三角形ADE,则∠BED为( )
A.45° B.15° C.10° D.125°
7.如图,正方形ABCD的边长为8,M在DC上,且DM=2,N是AC上一动点,则DN+MN的最小值为( )
A.6 B.8 C.12 D.10
8.如图,在边长为4的正方形ABCD中,E是AB边上的一点,且AE=3,Q为对角线AC上的动点,则△BEQ周长的最小值为( )
A.5 B.6 C. D.8
9.如图,将正方形OABC放在平面直角坐标系中,O是原点,点A的坐标为(1,),则点C的坐标为( )
A.(-,1) B.(-1,) C.(,1) D.(-,-1)
10.将n个边长都为1cm的正方形按如图所示的方法摆放,点A1,A2,…,An分别是正方形对角线的交点,则n个正方形重叠形成的重叠部分的面积和为( )
A.cm2 B.cm2 C. cm2 D.()ncm2
11.为增加绿化面积,某小区将原来正方形地砖更换为如图所示的正八边形植草砖,更换后,图中阴影部分为植草区域,设正八边形与其内部小正方形的边长都为a,则阴影部分的面积为( )
A.2a2 B.3a2 C.4a2 D.5a2
12.如图,已知方格纸中是4个相同的正方形,则∠1+∠2+∠3的度数为( )
A.90° B.105° C.120° D.135°
13.如图,在正方形ABCD外侧,作等边三角形ADE,AC,BE相交于点F,则∠BFC为( )
A.75° B.60° C.55° D.45°
14.如图,正方形ABCD中,点E是AD边的中点,BD,CE交于点H,BE、AH交于点G,则下列结论:
①∠ABE=∠DCE;②∠AHB=∠EHD;③S△BHE=S△CHD;④AG⊥BE.其中正确的是( )
A.①③ B.①②③④ C.①②③ D.①③④
15.若正方形的对角线长为2 cm,则这个正方形的面积为( )
A.4 B.2 C. D.
16.如图,以正方形的边为边向正方形外作等边,与交于点F,则的度数是( )
A.105° B.120° C.135° D.150°
17.如图,矩形纸片ABCD中,AB=6cm,BC=8cm.现将其沿AE对折,使得点B落在边AD上的点B1处,折痕与边BC交于点E,则CB1的长为( )
A.cm B.cm C.8cm D.10cm
18.如图,在正方形ABCD中,E为DC边上的一点,沿线段BE对折后,若∠ABF比∠EBF大15°,则∠EBF的度数为( )
A.15° B.20° C.25° D.30°
19.如图,正方形的两边在坐标轴上,,,点P为OB上一动点,的最小值是( )
A.8 B.10 C. D.
20.如图,点是中斜边(不与,重合)上一动点,分别作于点,作于点,连接、,若,,当点在斜边上运动时,则的最小值是( )
A.1.5 B.2
C.4.8 D.2.4
21.如图,正方形中,,点E在边上,且.将沿对折至,延长交边于点G,连接、.则下列结论:①;②;③;④,错误的是( )
A.① B.② C.③ D.④
22.如图,已知正方形的面积为平方厘米,厘米,则的长为( )
A. B. C. D.
参考答案:
1.C
解:①两条对角线互相平分的四边形是平行四边形.是真命题;
②两条对角线相等的四边形是矩形,是假命题;
③两条对角线互相垂直的平行四边形是菱形,是真命题;
④有一组邻边相等且有一个角是直角的四边形是正方形,是假命题;
2.A
3.A
解:如图,把绕A逆时针旋转90°得到,
∴,
∴,
∴,
∴G、B、E三点共线,
∴,
∵,
∴,
∴,
∴,
在和中,
,
∴,
∴,
设,
∵,
∴,
则,
∴,
∵,
∴,
解得,,
∴的长为2.
4.B
解:要使矩形成为正方形,可根据正方形的判定定理解答:
(1)有一组邻边相等的矩形是正方形,
(2)对角线互相垂直的矩形是正方形.
添加,能使矩形成为正方形.
5.A
解:∵将长方形纸片折叠,A落在BC上的F处,
∴BA=BF,
∵折痕为BE,沿EF剪下,
∴四边形ABFE为矩形,
∴四边形ABEF为正方形.
故用的判定定理是;邻边相等的矩形是正方形.
6.A
是等边三角形,
,,
四边形是正方形,
,,
,,
,
.
7.D
解:如图,连接BM,
∵点B和点D关于直线AC对称,
∴NB=ND,
则BM就是DN+MN的最小值,
∵正方形ABCD的边长是8,DM=2,
∴CM=6,
∴BM==10,
∴DN+MN的最小值是10.
8.B
解:连接BD,DE,
∵四边形ABCD是正方形,
∴点B与点D关于直线AC对称,
∴DE的长即为BQ+QE的最小值,
∵DE=BQ+QE=
∴△BEQ周长的最小值=DE+BE=5+1=6.
故选B.
9.A
解:如图:过点A作AD⊥x轴于D,过点C作CE⊥x轴于E,
∵∠OAD+∠AOD=∠COE+∠AOD,
∴∠OAD=∠COE,
∵OC=OA,∠ODA=∠OEC=90°,
∴△OAD△OCE全等,
∴OE=AD=,CE=OD=1,
∴点C的坐标为(-,1),
10.B
由题意可得阴影部分面积等于正方形面积的,即是,5个这样的正方形重叠部分(阴影部分)的面积和为×4,n个这样的正方形重叠部分(阴影部分)的面积和为×(n-1)=cm2.
11.A
12.D
观察图形可知, 所在的三角形与3所在的三角形全等,
,
又,
.
13.B
解:∵四边形ABCD是正方形,
∴∠BAD=90°,AB=AD,∠BAF=45°,
∵△ADE是等边三角形,
∴∠DAE=60°,AD=AE,
∴∠BAE=90°+60°=150°,AB=AE,
∴∠ABE=∠AEB=(180° 150°)=15°,
∴∠BFC=∠BAF+∠ABE=45°+15°=60°;
14.B
解:四边形是正方形,是边上的中点,
,,,
,
,
故①正确;
∵四边形ABCD是正方形,
∴AB=BC, ∠ABD=∠CBD,
∵BH=BH,
∴,
,
,
,
故②正确;
,
,
,
即,
故③正确;
四边形是正方形,
,,,
,
,
,
,
,
,
,
故④正确;
15.B
如图,连接BD,
正方形ABCD中,,则BD=AC=2,
正方形的面积为=,
16.B
解:∵四边形ABCD是正方形,等边△CDE,
∴∠BCD =90°,∠ACB=45°,∠DCE=60°,CD=CE= CB,
∴∠CBE=∠CEB.
∵∠BCE=∠BCD+∠DCE=90°+60°=150°,
∴∠CBE=15°.
∵∠ACB=45°,
∴∠AFB=∠ACB+∠CBE=60°.
∴∠AFE=120°.
17.B
解:∵∠AB1E=∠B=90°,∠BAB1=90°,
∴四边形ABEB1为矩形,
又∵AB=AB1,
∴四边形ABEB1为正方形,
∴BE=AB=6cm,
∴EC=BC﹣BE=2cm,
∴CB1=cm.
18.C
解:∵∠EBF是∠CBE折叠形成,
∴∠EBF=∠CBE,
∵∠ABF ∠EBF=15°,∠ABF+∠EBF+∠CBE=90°,
∴∠EBF=25°,
19.C
正方形ABCO,
A、C两点关于OB对称,
连接CD,交OB于,
,
,
当C、P、D三点共线时,取最小值,
,,
,
20.C
解:如图所示:连接,
∵,于点,作于点,
∴四边形是矩形,
∴MN=BP,
∴的最小值就是BP最小,
,
当时,最小,
∴.
21.D
解:∵四边形ABCD为正方形,将沿对折至,
∴AB=AD=AF=CD=6,∠AFG=∠AFE=∠D=90°,
∴∠AFG =90°,
∵AG=AG,∠B=∠AFG=90°,
∴Rt△ABG≌Rt△AFG(HL),
∴BG=FG,
∵,
∴,EC=4,设BG=FG=x,则CG=6-x,
在直角△ECG中,根据勾股定理,得,
解得x=3.
∴BG=3=6-3=CG,①正确;
∵CG=BG,BG=GF,
∴CG=GF,
∴△FGC是等腰三角形,∠GFC=∠GCF.
又∵Rt△ABG≌Rt△AFG;
∴∠AGB=∠AGF,∠AGB+∠AGF=2∠AGB=180°-∠FGC=∠GFC+∠GCF=2∠GFC=2∠GCF,
∴∠AGB=∠AGF=∠GFC=∠GCF,
∴AG∥CF,②正确;
∵, ,
∴,③正确;
∵∠BAG=∠FAG,∠DAE=∠FAE,
又∵∠BAD=90°,
∴∠GAE=45°,
∴∠AGB+∠AED=180°-∠GAE=135°,④错误.
22.D
解:∵正方形的面积为平方厘米,
∴,厘米,
在中,
∵厘米,
∴(厘米),
