四川省成都市郫都区2022-2023学年高二下学期4月期中考试文科数学试题(含答案)
文档属性
| 名称 | 四川省成都市郫都区2022-2023学年高二下学期4月期中考试文科数学试题(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 585.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-12 14:43:59 | ||
图片预览




文档简介
郫都区2022—2023学年度下期期中考试
高二数学(文科)
说明:1.本卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,满分150分,时间120分钟.
所有试题均在答题卡相应的区域内作答.
第I卷(选择题 共60分)
一.选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是最符合题目要求的)
1.函数,其导函数为,则
A. B. C. D.
2.复数在复平面内表示的点的坐标为
A. B. C. D.
3.执行如图所示的程序框图,输出的结果是
A. B. C. D.
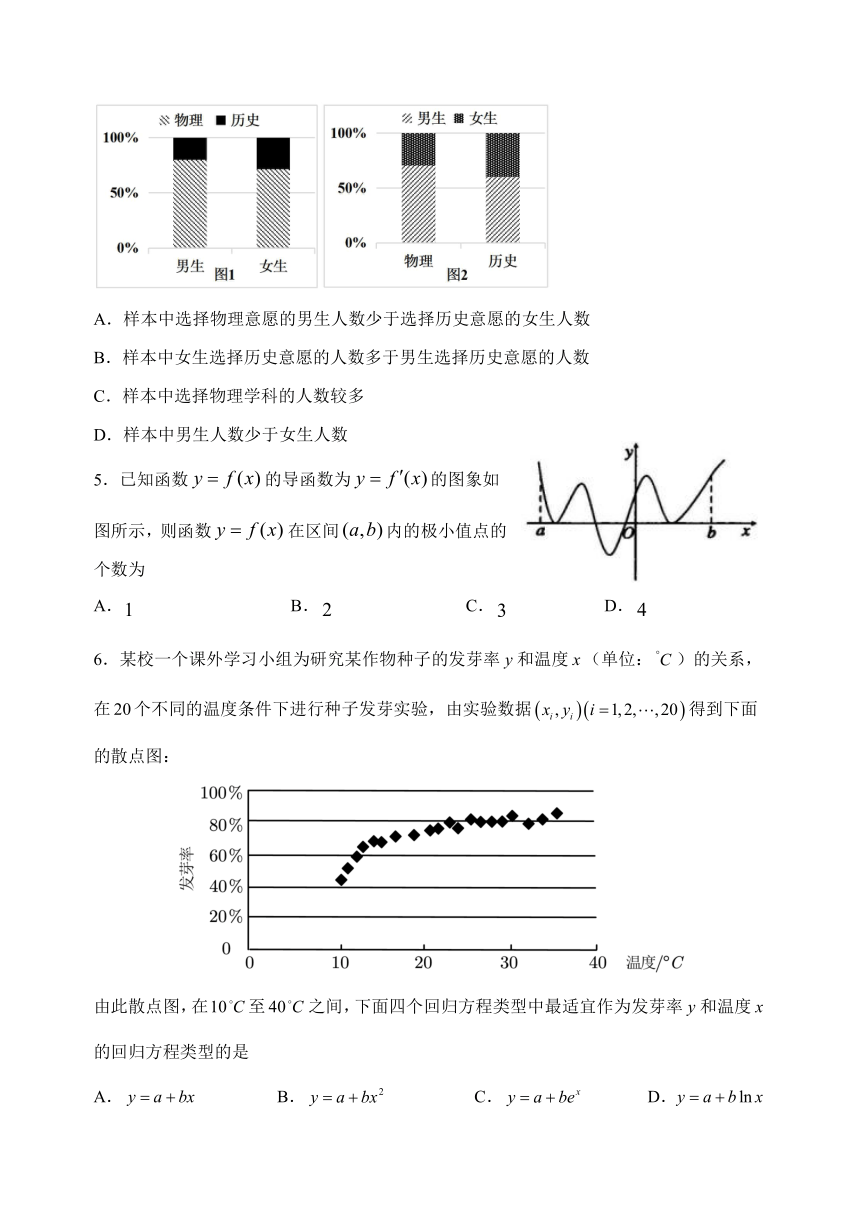
4.四川省从2022年秋季入学的高一年级学生开始实行高考综合改革,高考采用“3+1+2”模式,其中“1”为首选科目,即物理与历史二选一.某校为了解学生的首选意愿,对部分高一学生进行了抽样调查,制作出如下两个等高条形图,根据条形图信息,下列结论正确的是
A.样本中选择物理意愿的男生人数少于选择历史意愿的女生人数
B.样本中女生选择历史意愿的人数多于男生选择历史意愿的人数
C.样本中选择物理学科的人数较多
D.样本中男生人数少于女生人数
5.已知函数的导函数为的图象如图所示,则函数在区间内的极小值点的个数为
A. B. C. D.
6.某校一个课外学习小组为研究某作物种子的发芽率和温度(单位:)的关系,
在个不同的温度条件下进行种子发芽实验,由实验数据得到下面
的散点图:
由此散点图,在至之间,下面四个回归方程类型中最适宜作为发芽率和温度的回归方程类型的是
A. B. C. D.
7. 某产品的销售收入(万元)是产量x(千台)的函数,且函数解析式为,生产成本(万元)是产量x(千台)的函数,且函数解析式为,要使利润最大,则该产品应生产( )
A. 6千台 B. 7千台 C. 8千台 D. 9千台
8.在正整数范围内定义一种新的运算“*”,观察下列算式,
,,…,若,则的值为
A. 13 B. 14 C. 15 D. 16
9. 函数的最大值为
A. B. C. D.
10.已知,则的最大值为
A. B. C. D.
11.已知所有的三次函数都有对称中心,若函数,则
A. B. C. D.
12.已知函数. 若对任意,且,都有,则实数的取值范围是
A. B. C. D.
第II卷(非选择题 共90分)
注意事项: 必须使用0.5毫米黑色墨迹签字笔在答题卡上题目所指定的答题区域内作答,作图题可先用铅笔绘出,确认后再用0.5毫米黑色墨迹签字笔描清楚,答在试题卷上无效.
二.填空题(本大题共4小题,每小题5分,共20分)
13.复数的共轭复数为_______.
14.曲线的一条切线的斜率为,则该切线的方程为_______.
15.已知甲,乙,丙三人中,只有一个人会中国象棋. 甲说:“我会”;乙说:“我不会”;丙说:“甲不会”. 如果这三句话中只有一句是真的,那么甲,乙,丙三个人中会中国象棋的是_______.
16.已知函数的极小值小于0,则实数取值范围为_______.
三、解答题(本大题共6小题共70分,解答应写出文字说明,证明过程或演算步骤)
17.(本小题满分10分)
(1)求准线为的抛物线标准方程;
(2)求中心在原点,焦点在轴上,渐近线为,且实轴长为的双曲线标准方程.
18.(本小题满分12分)
已知函数在处取得极大值.
(1)求的值;
(2)当时,求的最大值.
19.(本小题满分12分)
数字人民币是由中国人民银行发行的数字形式的法定货币,由指定运营机构参与运营并向公众兑换,与纸钞和硬币等价.为了进一步了解普通大众对数字人民币的认知情况,某机构进行了一次问卷调查,统计结果如下:
小学及以下 初中 高中 大学专科 大学本科 硕士研究生及以上
不了解数字人民币 35 35 80 55 64 6
了解数字人民币 40 60 150 110 140 25
(1)如果将高中及以下学历称为“低学历”,大学专科及以上学历称为“高学历”,根据所给数据,完成下面的列联表;
低学历 高学历 合计
不了解数字人民币
了解数字人民币
合计 800
(2)根据(1)中所得列联表,判断是否有的把握认为“是否了解数字人民币”与“学历高低”有关?
附:,其中.
0.050 0.010 0001
K 3.841 6.635 10.828
20.(本小题满分12分)
某种农作物可以生长在滩涂和盐碱地,它的灌溉是将海水稀释后进行灌溉.某实验基地为了研究海水浓度(%)对亩产量(吨)的影响,通过在试验田的种植实验,测得了该农作物的亩产量与海水浓度的数据如下表.
绘制散点图发现,可以用线性回归模型拟合亩产量(吨)与海水浓度(%)之间的相关关系,用最小二乘法计算得与之间的线性回归方程为.
(1)求的值; (参考公式:)
(2)统计学中常用相关指数来刻画回归效果,越大,回归效果越好,如假设,就说明预报变量的差异有是解释变量引起的.请计算相关指数(精确到0.01),并指出亩产量的变化多大程度上是由灌溉海水浓度引起的?
21.(本小题满分12分)
设椭圆的离心率与双曲线的离心率互为倒数.
(1)求椭圆的方程;
(2)若直线交椭圆于两点,点为椭圆上的一点,求的面积取最大值时的直线方程.
22.(本小题满分12分)
设函数.
(1)若,求的单调区间;
(2)若对任意,都有,求实数a的取值范围.
郫都区2022—2023学年度下期期中考试
高二文科数学参考答案
一、选择题
1 2 3 4 5 6 7 8 9 10 11 12
A A C C A D A C A C A A
二、填空题
13、 14、 15、乙 16、
三、解答题
17、解:(1)准线为的抛物线标准方程为; ………………5分
(2)设双曲线标准方程为,
由实轴长为得, ………………7分
由渐近线得,即,
所以双曲线标准方程为. ………………10分
18、解:(1),且函数在处有极值1,
………………3分
解得 ………………5分
又当时,
在和上单调递增,在单调递减,
故在处取得极大值,满足题意.
综上,. ………………6分
(2)当,时,.则.
当变化时,与的变化情况如下表:
1 单调递减 极小值 单调递增 5
所以时,的最大值为. ………………12分
19、解:(1)根据所给数据,列联表为
低学历 高学历 合计
不了解数字人民币 150 125 275
了解数字人民币 250 275 525
合计 400 400 800
(2),所以
故没有的把握认为“是否了解数字人民币”与“学历高低”有关.
20、解:(1)因为, ………………2分
所以,即,
所以线性回归方程为, ………………4分
所以,
.
,
. ………………6分
(2),
所以相关指数.
故亩产量的变化有是由灌溉海水浓度引起的.
21、解:(1)的离心率为 ………………2分
所以在椭圆中,,得 ………………4分
所以椭圆的方程为. ………………5分
(2)由得,
由得, ………………6分
, ………………7分
………………8分
又到直线AB的距离为 ………………9分
当且仅当,即时取等号. ………………11分
所以的面积取最大值时的直线方程为或.
………………12分
22、解:(1)当时,,
令得;令得.
所以的单调递减区间为,单调递增区间为. ………………4分
(2)任意,都有,
即任意,都有.
,任意,都有.
设,则 ………………6分
设.
在上单调递减,,即. ………………10分
在上单调递减.
.
的取值范围是. ………………12分
高二数学(文科)
说明:1.本卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,满分150分,时间120分钟.
所有试题均在答题卡相应的区域内作答.
第I卷(选择题 共60分)
一.选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是最符合题目要求的)
1.函数,其导函数为,则
A. B. C. D.
2.复数在复平面内表示的点的坐标为
A. B. C. D.
3.执行如图所示的程序框图,输出的结果是
A. B. C. D.
4.四川省从2022年秋季入学的高一年级学生开始实行高考综合改革,高考采用“3+1+2”模式,其中“1”为首选科目,即物理与历史二选一.某校为了解学生的首选意愿,对部分高一学生进行了抽样调查,制作出如下两个等高条形图,根据条形图信息,下列结论正确的是
A.样本中选择物理意愿的男生人数少于选择历史意愿的女生人数
B.样本中女生选择历史意愿的人数多于男生选择历史意愿的人数
C.样本中选择物理学科的人数较多
D.样本中男生人数少于女生人数
5.已知函数的导函数为的图象如图所示,则函数在区间内的极小值点的个数为
A. B. C. D.
6.某校一个课外学习小组为研究某作物种子的发芽率和温度(单位:)的关系,
在个不同的温度条件下进行种子发芽实验,由实验数据得到下面
的散点图:
由此散点图,在至之间,下面四个回归方程类型中最适宜作为发芽率和温度的回归方程类型的是
A. B. C. D.
7. 某产品的销售收入(万元)是产量x(千台)的函数,且函数解析式为,生产成本(万元)是产量x(千台)的函数,且函数解析式为,要使利润最大,则该产品应生产( )
A. 6千台 B. 7千台 C. 8千台 D. 9千台
8.在正整数范围内定义一种新的运算“*”,观察下列算式,
,,…,若,则的值为
A. 13 B. 14 C. 15 D. 16
9. 函数的最大值为
A. B. C. D.
10.已知,则的最大值为
A. B. C. D.
11.已知所有的三次函数都有对称中心,若函数,则
A. B. C. D.
12.已知函数. 若对任意,且,都有,则实数的取值范围是
A. B. C. D.
第II卷(非选择题 共90分)
注意事项: 必须使用0.5毫米黑色墨迹签字笔在答题卡上题目所指定的答题区域内作答,作图题可先用铅笔绘出,确认后再用0.5毫米黑色墨迹签字笔描清楚,答在试题卷上无效.
二.填空题(本大题共4小题,每小题5分,共20分)
13.复数的共轭复数为_______.
14.曲线的一条切线的斜率为,则该切线的方程为_______.
15.已知甲,乙,丙三人中,只有一个人会中国象棋. 甲说:“我会”;乙说:“我不会”;丙说:“甲不会”. 如果这三句话中只有一句是真的,那么甲,乙,丙三个人中会中国象棋的是_______.
16.已知函数的极小值小于0,则实数取值范围为_______.
三、解答题(本大题共6小题共70分,解答应写出文字说明,证明过程或演算步骤)
17.(本小题满分10分)
(1)求准线为的抛物线标准方程;
(2)求中心在原点,焦点在轴上,渐近线为,且实轴长为的双曲线标准方程.
18.(本小题满分12分)
已知函数在处取得极大值.
(1)求的值;
(2)当时,求的最大值.
19.(本小题满分12分)
数字人民币是由中国人民银行发行的数字形式的法定货币,由指定运营机构参与运营并向公众兑换,与纸钞和硬币等价.为了进一步了解普通大众对数字人民币的认知情况,某机构进行了一次问卷调查,统计结果如下:
小学及以下 初中 高中 大学专科 大学本科 硕士研究生及以上
不了解数字人民币 35 35 80 55 64 6
了解数字人民币 40 60 150 110 140 25
(1)如果将高中及以下学历称为“低学历”,大学专科及以上学历称为“高学历”,根据所给数据,完成下面的列联表;
低学历 高学历 合计
不了解数字人民币
了解数字人民币
合计 800
(2)根据(1)中所得列联表,判断是否有的把握认为“是否了解数字人民币”与“学历高低”有关?
附:,其中.
0.050 0.010 0001
K 3.841 6.635 10.828
20.(本小题满分12分)
某种农作物可以生长在滩涂和盐碱地,它的灌溉是将海水稀释后进行灌溉.某实验基地为了研究海水浓度(%)对亩产量(吨)的影响,通过在试验田的种植实验,测得了该农作物的亩产量与海水浓度的数据如下表.
绘制散点图发现,可以用线性回归模型拟合亩产量(吨)与海水浓度(%)之间的相关关系,用最小二乘法计算得与之间的线性回归方程为.
(1)求的值; (参考公式:)
(2)统计学中常用相关指数来刻画回归效果,越大,回归效果越好,如假设,就说明预报变量的差异有是解释变量引起的.请计算相关指数(精确到0.01),并指出亩产量的变化多大程度上是由灌溉海水浓度引起的?
21.(本小题满分12分)
设椭圆的离心率与双曲线的离心率互为倒数.
(1)求椭圆的方程;
(2)若直线交椭圆于两点,点为椭圆上的一点,求的面积取最大值时的直线方程.
22.(本小题满分12分)
设函数.
(1)若,求的单调区间;
(2)若对任意,都有,求实数a的取值范围.
郫都区2022—2023学年度下期期中考试
高二文科数学参考答案
一、选择题
1 2 3 4 5 6 7 8 9 10 11 12
A A C C A D A C A C A A
二、填空题
13、 14、 15、乙 16、
三、解答题
17、解:(1)准线为的抛物线标准方程为; ………………5分
(2)设双曲线标准方程为,
由实轴长为得, ………………7分
由渐近线得,即,
所以双曲线标准方程为. ………………10分
18、解:(1),且函数在处有极值1,
………………3分
解得 ………………5分
又当时,
在和上单调递增,在单调递减,
故在处取得极大值,满足题意.
综上,. ………………6分
(2)当,时,.则.
当变化时,与的变化情况如下表:
1 单调递减 极小值 单调递增 5
所以时,的最大值为. ………………12分
19、解:(1)根据所给数据,列联表为
低学历 高学历 合计
不了解数字人民币 150 125 275
了解数字人民币 250 275 525
合计 400 400 800
(2),所以
故没有的把握认为“是否了解数字人民币”与“学历高低”有关.
20、解:(1)因为, ………………2分
所以,即,
所以线性回归方程为, ………………4分
所以,
.
,
. ………………6分
(2),
所以相关指数.
故亩产量的变化有是由灌溉海水浓度引起的.
21、解:(1)的离心率为 ………………2分
所以在椭圆中,,得 ………………4分
所以椭圆的方程为. ………………5分
(2)由得,
由得, ………………6分
, ………………7分
………………8分
又到直线AB的距离为 ………………9分
当且仅当,即时取等号. ………………11分
所以的面积取最大值时的直线方程为或.
………………12分
22、解:(1)当时,,
令得;令得.
所以的单调递减区间为,单调递增区间为. ………………4分
(2)任意,都有,
即任意,都有.
,任意,都有.
设,则 ………………6分
设.
在上单调递减,,即. ………………10分
在上单调递减.
.
的取值范围是. ………………12分
同课章节目录
