18.1 变量及其函数[下学期]
图片预览
文档简介
课题:变量和函数
课题:变量和函数
教材章节:§17.1
【教学目的】
了解常量和变量的意义,了解函数的三种表达方式。
通过对实际问题中数量之间互相依存关系的探索,理解函数概念。学会用函数思想去进行描述、研究其变化规律。
学会识别函数。
能根据实际情景列出函数关系式。
【知识重点】感受变化过程中存在的函数关系
【教学过程】
一、知识整理
1.一般的,如果在一个变化过程中有两个变量,例如x和y,对于x的每一个值,2.y都有唯一的值与之对应,我们就说x是自变量,y是因变量,此时也称y是x的函数。
3.表示函数关系的方法通常有三种:解析法、列表法和图象法。
4.在某一变化过程中,可以取不同数值的量叫做变量。取值始终不变的量叫做常量。
二、实例引入
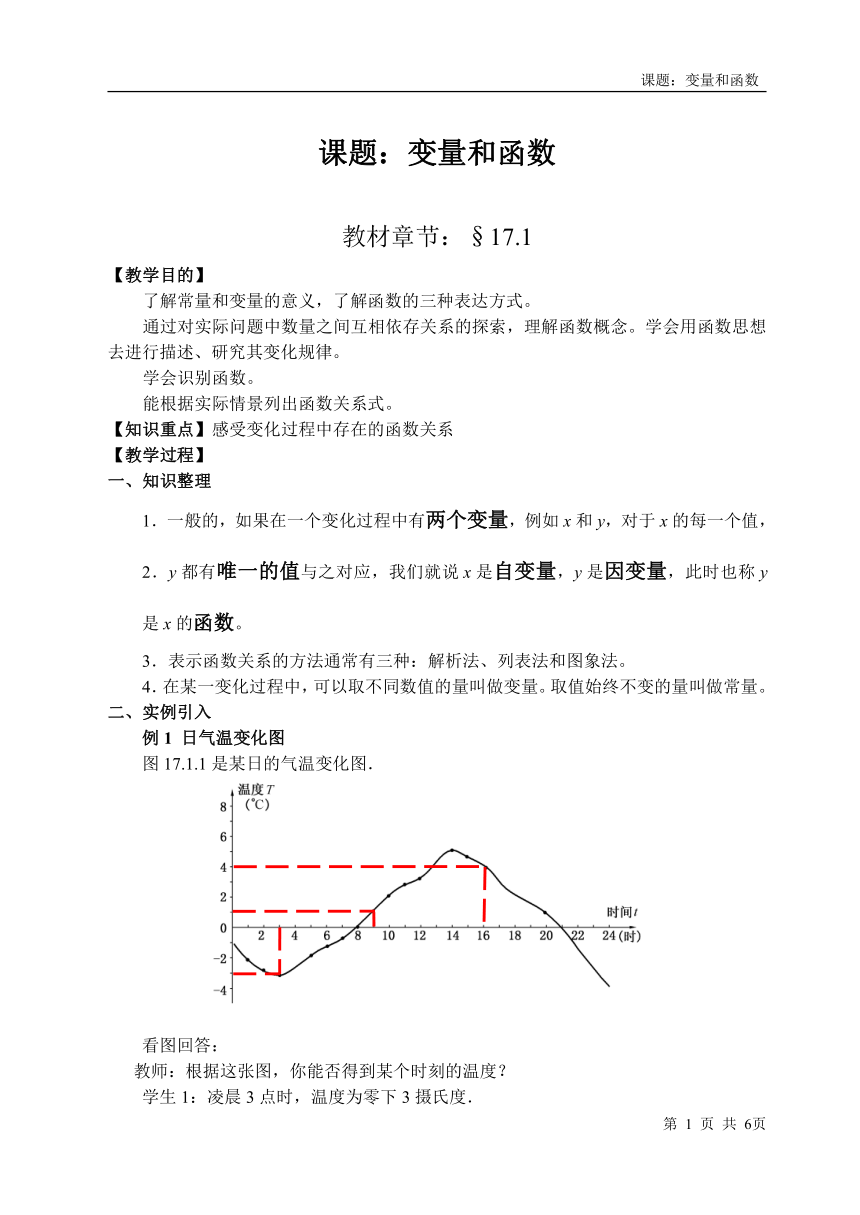
例1 日气温变化图
图17.1.1是某日的气温变化图.
看图回答:
教师:根据这张图,你能否得到某个时刻的温度?
学生1:凌晨3点时,温度为零下3摄氏度.
学生2:上午7点,温度为1摄氏度.
学生3:下午4点,温度为4摄氏度.
把以上这些数据填入表格
时间t 3 7 12 16 …
气温T -3 1 3 4 …
教师:在哪一段时间内,温度是上升的?
学生4:从凌晨3点起,到下午2点止,这期间温度是持续上升的.
教师:在这张图中,主要体现了那些数量的变化?
学生5:有温度的变化;学生6:还体现了时间的变化.
结论:从图中我们可以看到,随着时间t(时)的变化,相应地气温T(℃)也随之变化.每一个时间t,都有一个唯一的气温T与之对应.
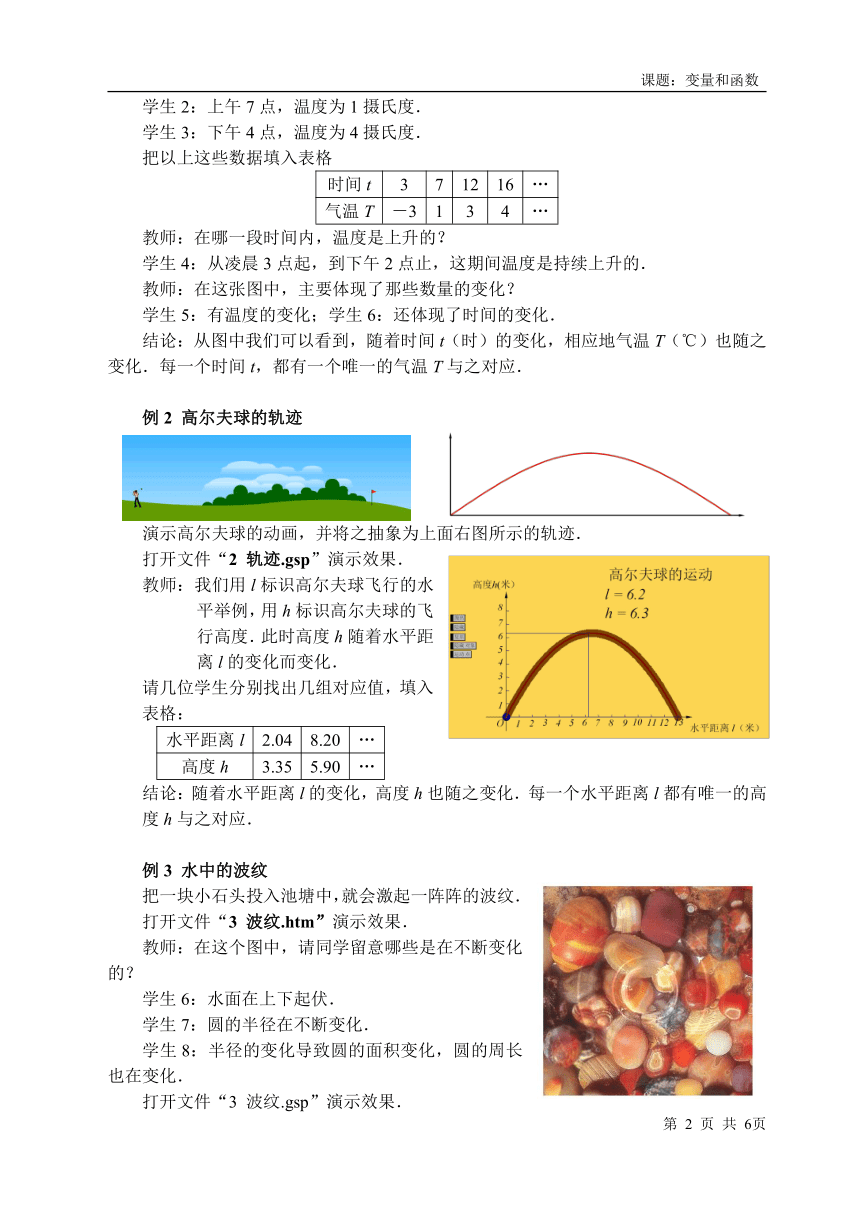
例2 高尔夫球的轨迹
演示高尔夫球的动画,并将之抽象为上面右图所示的轨迹.
打开文件“2 轨迹.gsp”演示效果.
教师:我们用l标识高尔夫球飞行的水平举例,用h标识高尔夫球的飞行高度.此时高度h随着水平距离l的变化而变化.
请几位学生分别找出几组对应值,填入表格:
水平距离l 2.04 8.20 …
高度h 3.35 5.90 …
结论:随着水平距离l的变化,高度h也随之变化.每一个水平距离l都有唯一的高度h与之对应.
例3 水中的波纹
把一块小石头投入池塘中,就会激起一阵阵的波纹.
打开文件“3 波纹.htm”演示效果.
教师:在这个图中,请同学留意哪些是在不断变化的?
学生6:水面在上下起伏.
学生7:圆的半径在不断变化.
学生8:半径的变化导致圆的面积变化,圆的周长也在变化.
打开文件“3 波纹.gsp”演示效果.
半径r 1 2 3 4 …
面积S π 4π 9π 16π …
结论:面积S随着半径r的变化而变化.每一个半径r都有唯一的一个面积S与之对应.
评注:考虑实例要尽量贴近学生的生活,所以对课本上提供的例子作了一些修改,最后选择了“一日内的温度变化”、“高尔夫球的运动”、“水中的波纹”这样三个例子.在上面的过程中,尽量让学生多观察,多留意在变化过程中的变量,感受“一个变量随着另一个变量的变化而变化”.
三、引出函数概念,并加以巩固
教师:以上实例的变化过程中,都有一些数量在变化,这样的量我们称为变量.如果在过程中,保持不变的就称为常量.一般的,如果在一个变化过程中有两个变量,例如x和y,对于x的每一个值,y都有唯一的值与之对应,我们就说x是自变量,y是因变量,此时也称y是x的函数。
在实例1中,时间t是自变量,气温T是因变量,对于时间t的每一个值,气温T都有唯一的值与之对应,称气温T是时间t的函数.
在实例2中,水平距离l是自变量……
(以下略)
带领学生,在每一个实例中重新巩固“自变量”、“因变量”、“函数”的概念.
四、函数的几种表达方式
从前面的几个实例中,来感受函数的各种表达方式
实例 一天的温度变化 高尔夫球的运动 水中的波纹
适用的表达方式 图像法,列表法 图像法,列表法,表达式 列表法,表达式
五、课堂活动
运行“04 现象.gsp”,演示效果:△ABC的高AD平移,底部BC不动.
教师:请同学们观察在屏幕上这个变化过程中,有哪些是变量?这些变量之间是否存在函数关系?如果存在函数关系,你准备用什么方法来表示这样的函数关系?
评注:这个课堂活动主要是巩固前面所学习的函数关系,学生在观察屏幕,寻找变量的过程中,自觉的运用函数的观念来看这个运动的图像,增强应用数学的意识.
六、其他
请学生根据自己的生活经验来举出一个例子,并将之表达出来。
评注:这个活动要求学生在本课前作一些准备工作。请每一位同学在课前都在预习的基础上,仿照课本上的问题,自己去身边寻找几个变量之间变化的关系,并设法记录下来。在课上请同学来讲讲自己身边的这些变化关系,分析表达的形式,变量和常量,自变量和因变量。但是同学有些可能找出来的并不是我们这里所说的函数关系,在课上要注意辩析清楚。
【小结与作业】
小节:本课主要学习了用函数的观念来分析一个变化的过程,同学在平时要多注意留意身边的现象,多尝试用数学的眼光去观察、分析.
作业:
1. 下表是某市2000年统计的该市男学生各年龄组的平均身高.
(1)从表中你能看出该市14岁的男学生的平均身高是多少吗
(2)该市男学生的平均身高从哪一岁开始迅速增加
(3)上表反映了哪些变量之间的关系 其中哪个是自变量 哪个是因变量
2. 写出下列各问题中的关系式,并指出其中的常量与变量:
(1)圆的周长C与半径r的关系式;
(2)火车以60千米/时的速度行驶,它驶过的路程s(千米)和所用时间t(时)的关系式;
(3)n边形的内角和S与边数n的关系式.
【课后心得】
华师大数学课本在初二下学期,引入了函数的概念以及一次函数和反比例函数的相关性质。§17.1作为整个一章的引入课,要引导学生探索具体问题中的数量关系和变化规律,通过简单实例,了解常量、变量的意义;结合实例,了解函数的概念和三种表示方法,能举出函数的实例。
这一节的内容是较多的,而且对于今后整个一章的学习、对于同学函数观念的形成都是至关重要的。结合教材内容,根据新课程标准,我觉得在教学中要抓住学生对变量的感悟、对函数的感悟、对表达的感悟.在教学中主要围绕数量关系来刻画变化规律,借助信息技术,按照“先宏观,再微观;先粗略,再细化,再严格”的步骤来进行本课的教学.通过本课,不但要解决学生学习中可能产生的困难,更要让学生初步的体会到函数的思想方法,为扎实的掌握函数相关知识打下基础.
服装尺寸对照表
男子服装(亚洲码)尺寸身高胸围腰围S1658874M1709278L1759682XL180100862XL18510490
1
第 1 页 共 6页
课题:变量和函数
教材章节:§17.1
【教学目的】
了解常量和变量的意义,了解函数的三种表达方式。
通过对实际问题中数量之间互相依存关系的探索,理解函数概念。学会用函数思想去进行描述、研究其变化规律。
学会识别函数。
能根据实际情景列出函数关系式。
【知识重点】感受变化过程中存在的函数关系
【教学过程】
一、知识整理
1.一般的,如果在一个变化过程中有两个变量,例如x和y,对于x的每一个值,2.y都有唯一的值与之对应,我们就说x是自变量,y是因变量,此时也称y是x的函数。
3.表示函数关系的方法通常有三种:解析法、列表法和图象法。
4.在某一变化过程中,可以取不同数值的量叫做变量。取值始终不变的量叫做常量。
二、实例引入
例1 日气温变化图
图17.1.1是某日的气温变化图.
看图回答:
教师:根据这张图,你能否得到某个时刻的温度?
学生1:凌晨3点时,温度为零下3摄氏度.
学生2:上午7点,温度为1摄氏度.
学生3:下午4点,温度为4摄氏度.
把以上这些数据填入表格
时间t 3 7 12 16 …
气温T -3 1 3 4 …
教师:在哪一段时间内,温度是上升的?
学生4:从凌晨3点起,到下午2点止,这期间温度是持续上升的.
教师:在这张图中,主要体现了那些数量的变化?
学生5:有温度的变化;学生6:还体现了时间的变化.
结论:从图中我们可以看到,随着时间t(时)的变化,相应地气温T(℃)也随之变化.每一个时间t,都有一个唯一的气温T与之对应.
例2 高尔夫球的轨迹
演示高尔夫球的动画,并将之抽象为上面右图所示的轨迹.
打开文件“2 轨迹.gsp”演示效果.
教师:我们用l标识高尔夫球飞行的水平举例,用h标识高尔夫球的飞行高度.此时高度h随着水平距离l的变化而变化.
请几位学生分别找出几组对应值,填入表格:
水平距离l 2.04 8.20 …
高度h 3.35 5.90 …
结论:随着水平距离l的变化,高度h也随之变化.每一个水平距离l都有唯一的高度h与之对应.
例3 水中的波纹
把一块小石头投入池塘中,就会激起一阵阵的波纹.
打开文件“3 波纹.htm”演示效果.
教师:在这个图中,请同学留意哪些是在不断变化的?
学生6:水面在上下起伏.
学生7:圆的半径在不断变化.
学生8:半径的变化导致圆的面积变化,圆的周长也在变化.
打开文件“3 波纹.gsp”演示效果.
半径r 1 2 3 4 …
面积S π 4π 9π 16π …
结论:面积S随着半径r的变化而变化.每一个半径r都有唯一的一个面积S与之对应.
评注:考虑实例要尽量贴近学生的生活,所以对课本上提供的例子作了一些修改,最后选择了“一日内的温度变化”、“高尔夫球的运动”、“水中的波纹”这样三个例子.在上面的过程中,尽量让学生多观察,多留意在变化过程中的变量,感受“一个变量随着另一个变量的变化而变化”.
三、引出函数概念,并加以巩固
教师:以上实例的变化过程中,都有一些数量在变化,这样的量我们称为变量.如果在过程中,保持不变的就称为常量.一般的,如果在一个变化过程中有两个变量,例如x和y,对于x的每一个值,y都有唯一的值与之对应,我们就说x是自变量,y是因变量,此时也称y是x的函数。
在实例1中,时间t是自变量,气温T是因变量,对于时间t的每一个值,气温T都有唯一的值与之对应,称气温T是时间t的函数.
在实例2中,水平距离l是自变量……
(以下略)
带领学生,在每一个实例中重新巩固“自变量”、“因变量”、“函数”的概念.
四、函数的几种表达方式
从前面的几个实例中,来感受函数的各种表达方式
实例 一天的温度变化 高尔夫球的运动 水中的波纹
适用的表达方式 图像法,列表法 图像法,列表法,表达式 列表法,表达式
五、课堂活动
运行“04 现象.gsp”,演示效果:△ABC的高AD平移,底部BC不动.
教师:请同学们观察在屏幕上这个变化过程中,有哪些是变量?这些变量之间是否存在函数关系?如果存在函数关系,你准备用什么方法来表示这样的函数关系?
评注:这个课堂活动主要是巩固前面所学习的函数关系,学生在观察屏幕,寻找变量的过程中,自觉的运用函数的观念来看这个运动的图像,增强应用数学的意识.
六、其他
请学生根据自己的生活经验来举出一个例子,并将之表达出来。
评注:这个活动要求学生在本课前作一些准备工作。请每一位同学在课前都在预习的基础上,仿照课本上的问题,自己去身边寻找几个变量之间变化的关系,并设法记录下来。在课上请同学来讲讲自己身边的这些变化关系,分析表达的形式,变量和常量,自变量和因变量。但是同学有些可能找出来的并不是我们这里所说的函数关系,在课上要注意辩析清楚。
【小结与作业】
小节:本课主要学习了用函数的观念来分析一个变化的过程,同学在平时要多注意留意身边的现象,多尝试用数学的眼光去观察、分析.
作业:
1. 下表是某市2000年统计的该市男学生各年龄组的平均身高.
(1)从表中你能看出该市14岁的男学生的平均身高是多少吗
(2)该市男学生的平均身高从哪一岁开始迅速增加
(3)上表反映了哪些变量之间的关系 其中哪个是自变量 哪个是因变量
2. 写出下列各问题中的关系式,并指出其中的常量与变量:
(1)圆的周长C与半径r的关系式;
(2)火车以60千米/时的速度行驶,它驶过的路程s(千米)和所用时间t(时)的关系式;
(3)n边形的内角和S与边数n的关系式.
【课后心得】
华师大数学课本在初二下学期,引入了函数的概念以及一次函数和反比例函数的相关性质。§17.1作为整个一章的引入课,要引导学生探索具体问题中的数量关系和变化规律,通过简单实例,了解常量、变量的意义;结合实例,了解函数的概念和三种表示方法,能举出函数的实例。
这一节的内容是较多的,而且对于今后整个一章的学习、对于同学函数观念的形成都是至关重要的。结合教材内容,根据新课程标准,我觉得在教学中要抓住学生对变量的感悟、对函数的感悟、对表达的感悟.在教学中主要围绕数量关系来刻画变化规律,借助信息技术,按照“先宏观,再微观;先粗略,再细化,再严格”的步骤来进行本课的教学.通过本课,不但要解决学生学习中可能产生的困难,更要让学生初步的体会到函数的思想方法,为扎实的掌握函数相关知识打下基础.
服装尺寸对照表
男子服装(亚洲码)尺寸身高胸围腰围S1658874M1709278L1759682XL180100862XL18510490
1
第 1 页 共 6页
