四川省宜宾市高县2022-2023学年高二下学期期中考试数学(文)试题(Word版含答案)
文档属性
| 名称 | 四川省宜宾市高县2022-2023学年高二下学期期中考试数学(文)试题(Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 271.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-12 16:10:13 | ||
图片预览


文档简介
高县2022-2023学年高二下学期期中考试
文科数学
1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共4页,满分150分,考试时间120分钟;
2.答题前,考生务必将自己的姓名、考号填写在答题卡相应的位置;
3.全部答案在答题卡上完成,答在本试卷上无效;
4.考试结束后,交回答题卡.
第Ⅰ卷
选择题:本题共12个小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合要求的。
1.命题“,使”的否定是( )
A. ,使 B. ,使
C. ,使 D. ,使
2. 已知,向量,则“”是“”的( )
A. 必要不充分条件 B. 充分不必要条件
C. 充分必要条件 D. 即不充分也不必要条件
3. 已知多项式,当时的函数值时用秦九韶算法计算的值是( )
A. B. C. D.
4.已知命题空间中两条直线没有公共点,则这两条直线平行命题空间中三个平面,,,若,,,则则下列命题为真命题的是( )
A. B. C. D.
5. 一个袋中装有大小、质地相同的个红球和个黑球,从中随机摸出个球,设事件“至少有个黑球”,下列事件中,与事件互斥而不互为对立的是( )
A. 都是黑球 B. 恰好有个黑球 C. 恰好有个红球 D. 至少有个红球
6.若函数,则( )
A. B.
C. D.
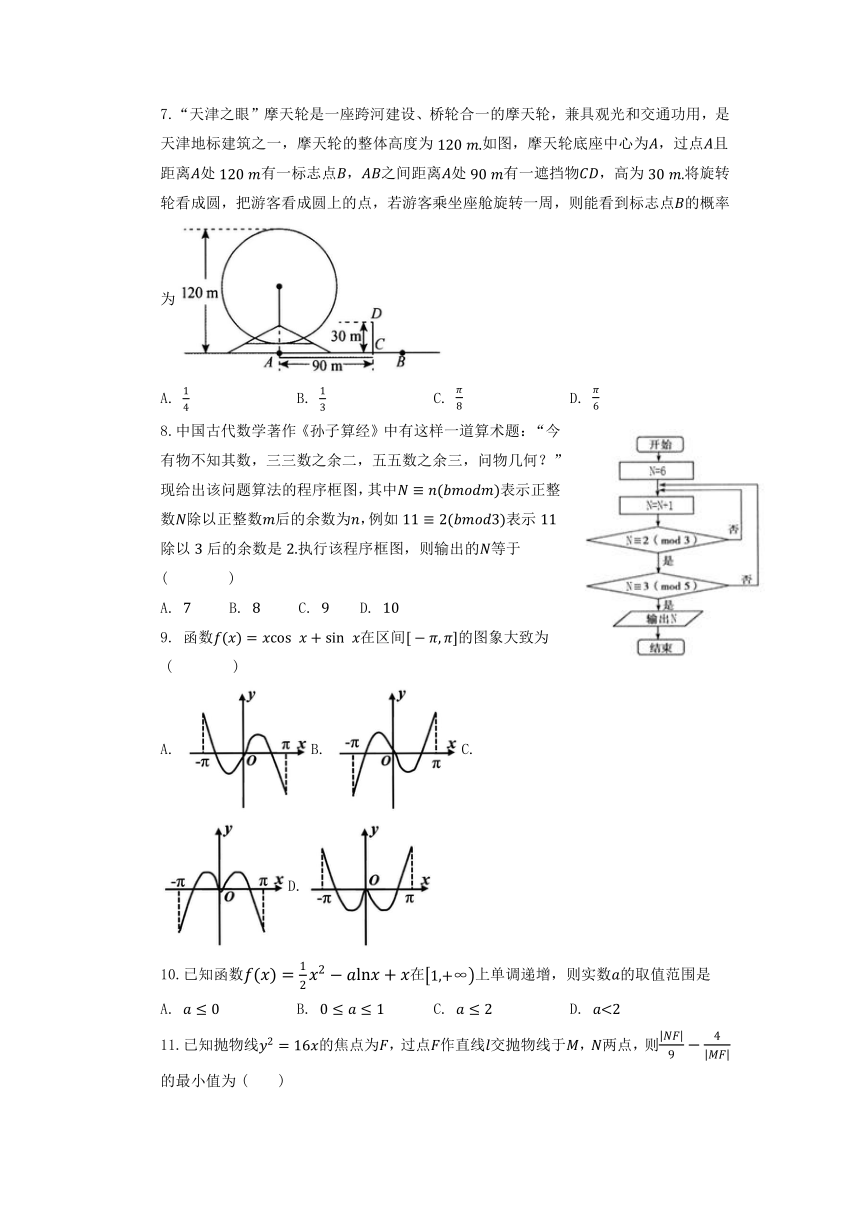
7.“天津之眼”摩天轮是一座跨河建设、桥轮合一的摩天轮,兼具观光和交通功用,是天津地标建筑之一,摩天轮的整体高度为如图,摩天轮底座中心为,过点且距离处有一标志点,之间距离处有一遮挡物,高为将旋转轮看成圆,把游客看成圆上的点,若游客乘坐座舱旋转一周,则能看到标志点的概率为
A. B. C. D.
8.中国古代数学著作《孙子算经》中有这样一道算术题:“今有物不知其数,三三数之余二,五五数之余三,问物几何?”现给出该问题算法的程序框图,其中表示正整数除以正整数后的余数为,例如表示除以后的余数是执行该程序框图,则输出的等于( )
A. B. C. D.
9. 函数 在区间的图象大致为( )
A. B. C. D.
10.已知函数在上单调递增,则实数的取值范围是
A. B. C. D.
11.已知抛物线的焦点为,过点作直线交抛物线于,两点,则的最小值为( )
A. B. C. D.
12. 已知函数,,若,,使得,则实数的取值范围是( )
A. B.
C. D.
第Ⅱ卷
二、填空题:本大题共4个小题,每小题5分,共20分,请把答案直接填在答题卡相应横线上。
13. 命题“若,都是实数,则”的否命题是______.
14.若函数在处取得极小值,则实数的取值范围是__________.
15.某莲藕种植塘每年的固定成本是万元,每年最大规模的种植量是万千克,每种植万千克莲藕,成本增加万元销售额单位:万元与莲藕种植量单位:万千克满足为常数,若种植万千克,销售利润是万元,则要使销售利润最大,每年需种植莲藕___________万千克.
16. 已知为定义在上的可导函数,且,则不等式的解集为 .
三、解答题:本大题共6小题,共70分,解答时应写出必要的文字说明、证明过程或演算步骤。
17.(本小题10分)
已知函数.
求函数的单调递减区间;
求函数在上的最大值和最小值.
18.(本小题12分)
已知.
当时,求曲线在点处的切线方程;
若对恒成立,求的取值范围.
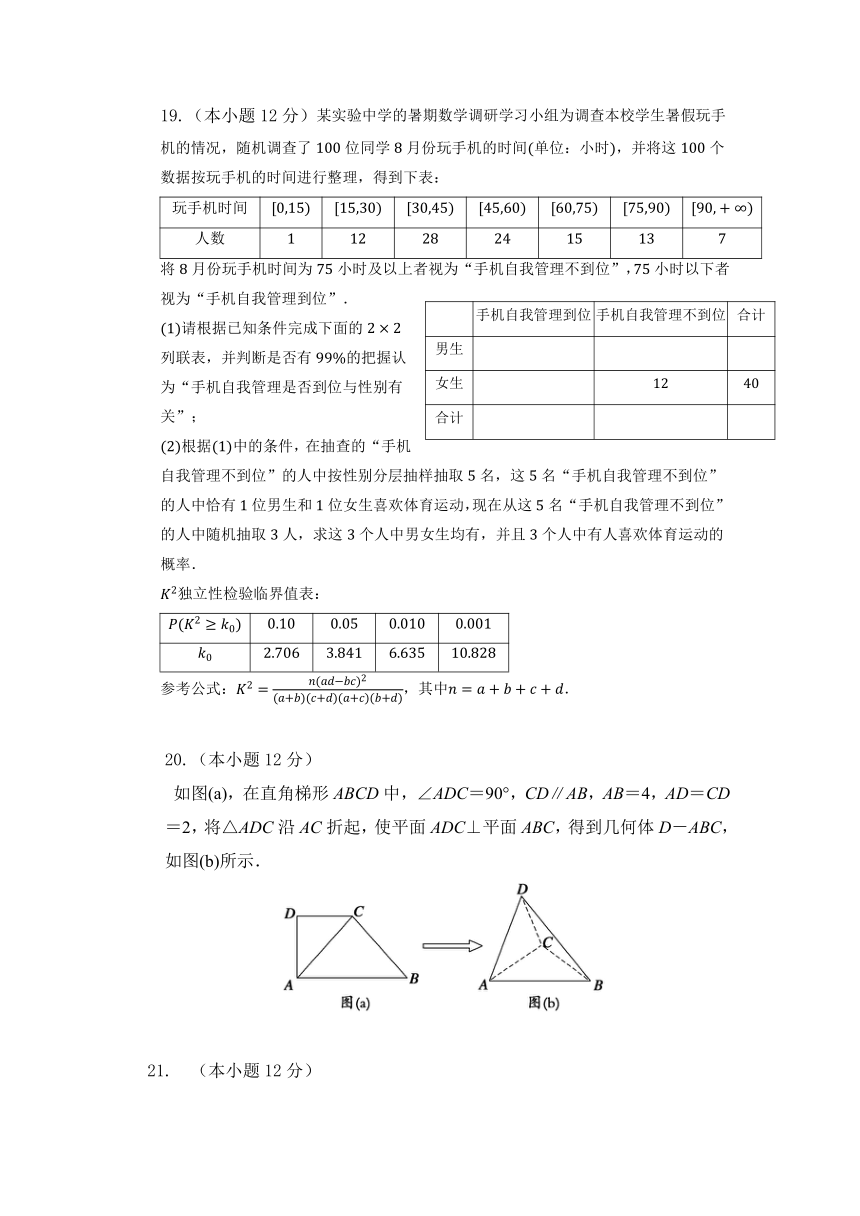
19.(本小题12分)某实验中学的暑期数学调研学习小组为调查本校学生暑假玩手机的情况,随机调查了位同学月份玩手机的时间单位:小时,并将这个数据按玩手机的时间进行整理,得到下表:
玩手机时间
人数
手机自我管理到位 手机自我管理不到位 合计
男生
女生
合计
将月份玩手机时间为小时及以上者视为“手机自我管理不到位”,小时以下者视为“手机自我管理到位”.
请根据已知条件完成下面的列联表,并判断是否有的把握认为“手机自我管理是否到位与性别有关”;
根据中的条件,在抽查的“手机自我管理不到位”的人中按性别分层抽样抽取名,这名“手机自我管理不到位”的人中恰有位男生和位女生喜欢体育运动,现在从这名“手机自我管理不到位”的人中随机抽取人,求这个人中男女生均有,并且个人中有人喜欢体育运动的概率.
独立性检验临界值表:
参考公式:,其中.
20.(本小题12分)
如图(a),在直角梯形ABCD中,∠ADC=90°,CD∥AB,AB=4,AD=CD=2,将△ADC沿AC折起,使平面ADC⊥平面ABC,得到几何体D-ABC,如图(b)所示.
(本小题12分)
已知长轴长为的椭圆的一个焦点为.
(1)求椭圆C的方程;
(2)若斜率为l的直线交椭圆于,两点,且,求直线的方程.
22.(本小题12分)
常数,函数.
令时,求的最小值,并比较的最小值与零的大小
求证:在上是增函数
求证:当时,恒有.
数学参考答案与评分标准
一、选择题(本大题共12小题,每小题5分,共60分.)
题号 1 2 3 4 5 6 7 8 9 10 11 12
答案 B B C D B A A B A C D D
二、填空题(本大题共4小题,每小题5分,共20分.)
题号 答 案 题号 答 案
13 14
15 8 16
三、解答题(本大题共6小题,共74分.)
17.(本小题满分10分)
解:函数的导数为,
令,递减区间为:;
当变化时,与的变化情况如下:
极大值 极小值
,而,,,
.
18.当时,,,
,,
所以切线方程为:,即.
恒成立,即在上恒成立,
设,,
令,得,
在上,,
所以函数在上单调递减,
所以,,
故有.
19.(本小题满分12分):列联表如下:
手机自我管理到位 手机自我管理不到位 合计
男生
女生
合计
的观测值,
所以没有的把握认为“手机自我管理是否到位与性别有关”.
设这5名“手机自我管理不到位”的人中,2名男生记为,,3名女生记为,,,其
中喜欢运动的为,,
则从这名“手机自我管理不到位”的人中随机抽取人的所有结果组成的基本事件为
,,,,,,,,,,
以上共计个基本事件,且这些基本事件的出现是等可能的.
其中这个人中男女生均有,并且个人中有人喜欢体育运动的基本事件为,,
,,,,,,共计个事件,
故所求事件的概率.
20.(本小题满分12分)
解:(1)证明 在图中,可得AC=BC=2,
从而AC2+BC2=AB2,
故AC⊥BC,
又平面ADC⊥平面ABC,平面ADC∩平面ABC=AC,BC 平面ABC,∴BC⊥平面ACD.
(2)解 由(1)可知,BC为三棱锥B-ACD的高,BC=2,S△ACD=2,
∴VB-ACD=S△ACD·BC=×2×2=,
由等体积性可知,几何体D-ABC的体积为.
21.(本小题满分12分)
解:1.由题意,,,
∴,
∴椭圆的方程为.
2.设直线的方程为,点,
联立方程组
化简,得,
,即,
且,,
∴
解得,符合题意,
∴直线的方程为或.
22.(本小题满分12分)
解:因为,
所以.
所以,
所以,令,得.
列表如下:
减 极小值 增
所以在处取得极小值 ,
即 的最小值为,
因为 ,所以 ,又,所以
由知,的最小值为正数,
所以对一切 ,恒有.
从而当时,恒有 ,
故在 上是增函数.
由知在 上是增函数,
所以当时,.
又 ,
所以 ,即 ,
所以,
故当 时,恒有.
文科数学
1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共4页,满分150分,考试时间120分钟;
2.答题前,考生务必将自己的姓名、考号填写在答题卡相应的位置;
3.全部答案在答题卡上完成,答在本试卷上无效;
4.考试结束后,交回答题卡.
第Ⅰ卷
选择题:本题共12个小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合要求的。
1.命题“,使”的否定是( )
A. ,使 B. ,使
C. ,使 D. ,使
2. 已知,向量,则“”是“”的( )
A. 必要不充分条件 B. 充分不必要条件
C. 充分必要条件 D. 即不充分也不必要条件
3. 已知多项式,当时的函数值时用秦九韶算法计算的值是( )
A. B. C. D.
4.已知命题空间中两条直线没有公共点,则这两条直线平行命题空间中三个平面,,,若,,,则则下列命题为真命题的是( )
A. B. C. D.
5. 一个袋中装有大小、质地相同的个红球和个黑球,从中随机摸出个球,设事件“至少有个黑球”,下列事件中,与事件互斥而不互为对立的是( )
A. 都是黑球 B. 恰好有个黑球 C. 恰好有个红球 D. 至少有个红球
6.若函数,则( )
A. B.
C. D.
7.“天津之眼”摩天轮是一座跨河建设、桥轮合一的摩天轮,兼具观光和交通功用,是天津地标建筑之一,摩天轮的整体高度为如图,摩天轮底座中心为,过点且距离处有一标志点,之间距离处有一遮挡物,高为将旋转轮看成圆,把游客看成圆上的点,若游客乘坐座舱旋转一周,则能看到标志点的概率为
A. B. C. D.
8.中国古代数学著作《孙子算经》中有这样一道算术题:“今有物不知其数,三三数之余二,五五数之余三,问物几何?”现给出该问题算法的程序框图,其中表示正整数除以正整数后的余数为,例如表示除以后的余数是执行该程序框图,则输出的等于( )
A. B. C. D.
9. 函数 在区间的图象大致为( )
A. B. C. D.
10.已知函数在上单调递增,则实数的取值范围是
A. B. C. D.
11.已知抛物线的焦点为,过点作直线交抛物线于,两点,则的最小值为( )
A. B. C. D.
12. 已知函数,,若,,使得,则实数的取值范围是( )
A. B.
C. D.
第Ⅱ卷
二、填空题:本大题共4个小题,每小题5分,共20分,请把答案直接填在答题卡相应横线上。
13. 命题“若,都是实数,则”的否命题是______.
14.若函数在处取得极小值,则实数的取值范围是__________.
15.某莲藕种植塘每年的固定成本是万元,每年最大规模的种植量是万千克,每种植万千克莲藕,成本增加万元销售额单位:万元与莲藕种植量单位:万千克满足为常数,若种植万千克,销售利润是万元,则要使销售利润最大,每年需种植莲藕___________万千克.
16. 已知为定义在上的可导函数,且,则不等式的解集为 .
三、解答题:本大题共6小题,共70分,解答时应写出必要的文字说明、证明过程或演算步骤。
17.(本小题10分)
已知函数.
求函数的单调递减区间;
求函数在上的最大值和最小值.
18.(本小题12分)
已知.
当时,求曲线在点处的切线方程;
若对恒成立,求的取值范围.
19.(本小题12分)某实验中学的暑期数学调研学习小组为调查本校学生暑假玩手机的情况,随机调查了位同学月份玩手机的时间单位:小时,并将这个数据按玩手机的时间进行整理,得到下表:
玩手机时间
人数
手机自我管理到位 手机自我管理不到位 合计
男生
女生
合计
将月份玩手机时间为小时及以上者视为“手机自我管理不到位”,小时以下者视为“手机自我管理到位”.
请根据已知条件完成下面的列联表,并判断是否有的把握认为“手机自我管理是否到位与性别有关”;
根据中的条件,在抽查的“手机自我管理不到位”的人中按性别分层抽样抽取名,这名“手机自我管理不到位”的人中恰有位男生和位女生喜欢体育运动,现在从这名“手机自我管理不到位”的人中随机抽取人,求这个人中男女生均有,并且个人中有人喜欢体育运动的概率.
独立性检验临界值表:
参考公式:,其中.
20.(本小题12分)
如图(a),在直角梯形ABCD中,∠ADC=90°,CD∥AB,AB=4,AD=CD=2,将△ADC沿AC折起,使平面ADC⊥平面ABC,得到几何体D-ABC,如图(b)所示.
(本小题12分)
已知长轴长为的椭圆的一个焦点为.
(1)求椭圆C的方程;
(2)若斜率为l的直线交椭圆于,两点,且,求直线的方程.
22.(本小题12分)
常数,函数.
令时,求的最小值,并比较的最小值与零的大小
求证:在上是增函数
求证:当时,恒有.
数学参考答案与评分标准
一、选择题(本大题共12小题,每小题5分,共60分.)
题号 1 2 3 4 5 6 7 8 9 10 11 12
答案 B B C D B A A B A C D D
二、填空题(本大题共4小题,每小题5分,共20分.)
题号 答 案 题号 答 案
13 14
15 8 16
三、解答题(本大题共6小题,共74分.)
17.(本小题满分10分)
解:函数的导数为,
令,递减区间为:;
当变化时,与的变化情况如下:
极大值 极小值
,而,,,
.
18.当时,,,
,,
所以切线方程为:,即.
恒成立,即在上恒成立,
设,,
令,得,
在上,,
所以函数在上单调递减,
所以,,
故有.
19.(本小题满分12分):列联表如下:
手机自我管理到位 手机自我管理不到位 合计
男生
女生
合计
的观测值,
所以没有的把握认为“手机自我管理是否到位与性别有关”.
设这5名“手机自我管理不到位”的人中,2名男生记为,,3名女生记为,,,其
中喜欢运动的为,,
则从这名“手机自我管理不到位”的人中随机抽取人的所有结果组成的基本事件为
,,,,,,,,,,
以上共计个基本事件,且这些基本事件的出现是等可能的.
其中这个人中男女生均有,并且个人中有人喜欢体育运动的基本事件为,,
,,,,,,共计个事件,
故所求事件的概率.
20.(本小题满分12分)
解:(1)证明 在图中,可得AC=BC=2,
从而AC2+BC2=AB2,
故AC⊥BC,
又平面ADC⊥平面ABC,平面ADC∩平面ABC=AC,BC 平面ABC,∴BC⊥平面ACD.
(2)解 由(1)可知,BC为三棱锥B-ACD的高,BC=2,S△ACD=2,
∴VB-ACD=S△ACD·BC=×2×2=,
由等体积性可知,几何体D-ABC的体积为.
21.(本小题满分12分)
解:1.由题意,,,
∴,
∴椭圆的方程为.
2.设直线的方程为,点,
联立方程组
化简,得,
,即,
且,,
∴
解得,符合题意,
∴直线的方程为或.
22.(本小题满分12分)
解:因为,
所以.
所以,
所以,令,得.
列表如下:
减 极小值 增
所以在处取得极小值 ,
即 的最小值为,
因为 ,所以 ,又,所以
由知,的最小值为正数,
所以对一切 ,恒有.
从而当时,恒有 ,
故在 上是增函数.
由知在 上是增函数,
所以当时,.
又 ,
所以 ,即 ,
所以,
故当 时,恒有.
同课章节目录
