18.1 函数与变量[下学期]
图片预览

文档简介
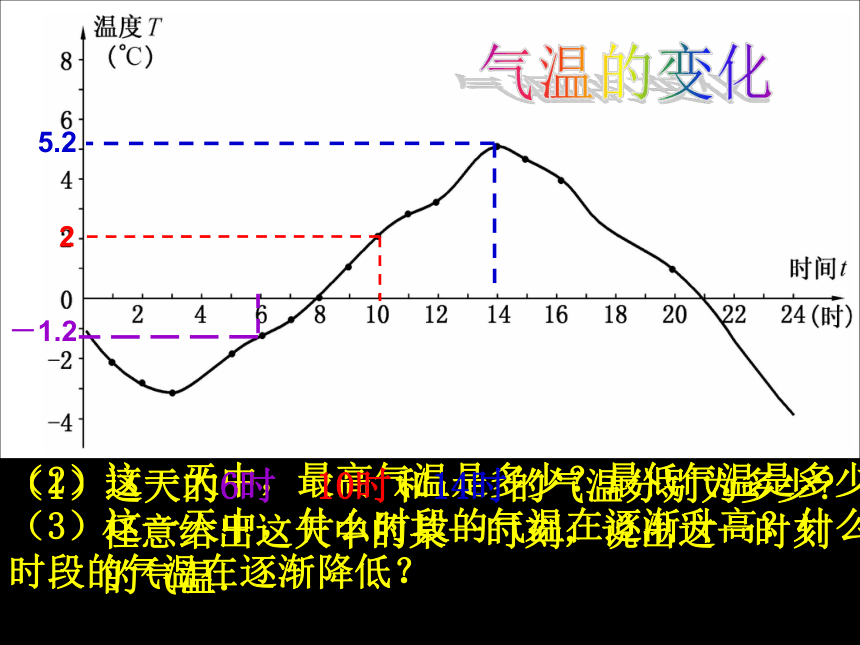
课件7张PPT。变量与函数数学上常用来刻画各种运动变化(2)这一天中,最高气温是多少?最低气温是多少?
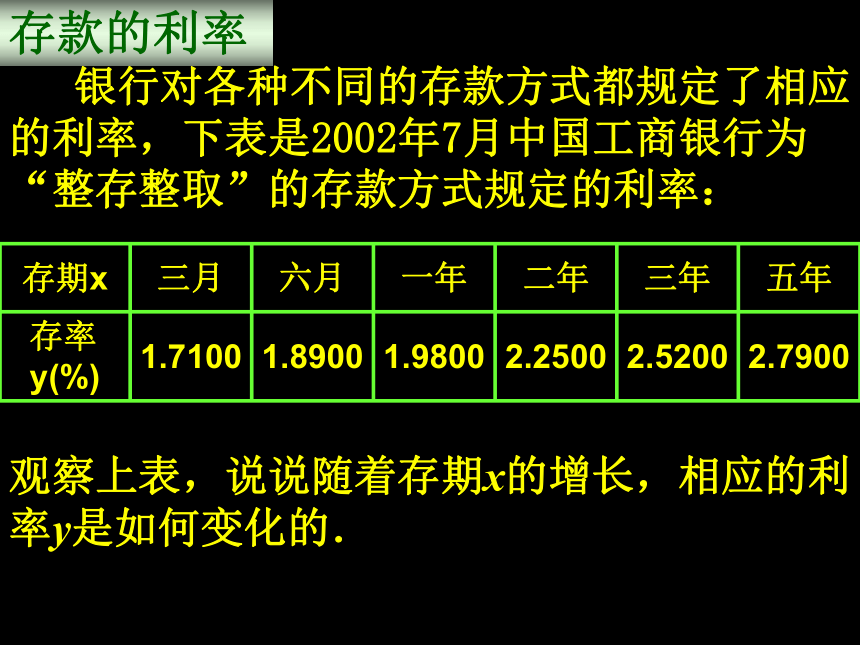
(3)这一天中,什么时段的气温在逐渐升高?什么时段的气温在逐渐降低? (1)这天的6时、10时和14时的气温分别为多少?任意给出这天中的某一时刻,说出这一时刻的气温. -1.225.2气温的变化 银行对各种不同的存款方式都规定了相应的利率,下表是2002年7月中国工商银行为“整存整取”的存款方式规定的利率:观察上表,说说随着存期x的增长,相应的利率y是如何变化的. 存款的利率收音机上的刻度盘的波长和频率分别是用米(m)和千赫兹(kHz)为单位标刻的.下面是一些对应的数:你能发现每一组l、f的值之间的关系吗? l 与 f 的乘积是一个定值,即lf=300 000,
或者说 f=说明波长l 越大,频率f 就____________.越小函数的关系式rS圆=πr2利用这个关系式,填写下表: π2.25π4π6.76π10.24π由此可以看出,圆的半径越大,它的面积就______________.越大函数的关系式在某一变化过程中,可以取不同数值的量,叫做变量. 气温问题存款利率波长与频率的问题圆面积
问题还有一种量,它的取值始终保持不变,我们称之为常量 如果在一个变化过程中,有两个变量,例如 x 和 y,对于 x 的每一个值,y 都有唯一的值与之对应,我们就说x是自变量,y 是因变量,此时也称 y 是 x 的函数表示函数关系的方法通常有三种:
(1) 解析法;
(2) 列表法;
(3) 图象法。表示函数关系的方法通常有三种:
(1) 解析法:如问题3中的f = ,问题4中的S=πr 2,这些表达式称为函数的关系式.
(2)列表法:如问题2中的利率表,问题3中的波长与频率关系表.
(3) 图象法:问题1中的气温曲线. 3、表示函数关系的方法:
(3)这一天中,什么时段的气温在逐渐升高?什么时段的气温在逐渐降低? (1)这天的6时、10时和14时的气温分别为多少?任意给出这天中的某一时刻,说出这一时刻的气温. -1.225.2气温的变化 银行对各种不同的存款方式都规定了相应的利率,下表是2002年7月中国工商银行为“整存整取”的存款方式规定的利率:观察上表,说说随着存期x的增长,相应的利率y是如何变化的. 存款的利率收音机上的刻度盘的波长和频率分别是用米(m)和千赫兹(kHz)为单位标刻的.下面是一些对应的数:你能发现每一组l、f的值之间的关系吗? l 与 f 的乘积是一个定值,即lf=300 000,
或者说 f=说明波长l 越大,频率f 就____________.越小函数的关系式rS圆=πr2利用这个关系式,填写下表: π2.25π4π6.76π10.24π由此可以看出,圆的半径越大,它的面积就______________.越大函数的关系式在某一变化过程中,可以取不同数值的量,叫做变量. 气温问题存款利率波长与频率的问题圆面积
问题还有一种量,它的取值始终保持不变,我们称之为常量 如果在一个变化过程中,有两个变量,例如 x 和 y,对于 x 的每一个值,y 都有唯一的值与之对应,我们就说x是自变量,y 是因变量,此时也称 y 是 x 的函数表示函数关系的方法通常有三种:
(1) 解析法;
(2) 列表法;
(3) 图象法。表示函数关系的方法通常有三种:
(1) 解析法:如问题3中的f = ,问题4中的S=πr 2,这些表达式称为函数的关系式.
(2)列表法:如问题2中的利率表,问题3中的波长与频率关系表.
(3) 图象法:问题1中的气温曲线. 3、表示函数关系的方法:
