等比数列的前n项和(福建省漳州市平和县)
文档属性
| 名称 | 等比数列的前n项和(福建省漳州市平和县) |

|
|
| 格式 | rar | ||
| 文件大小 | 310.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-09-08 00:00:00 | ||
图片预览






文档简介
课件15张PPT。等比数列的前n项和(一)一个数学游戏问题: 甲、乙二人约定在一个月(按30天)内甲每天给乙100元钱,而乙则第一天给甲返还一分,第二天给甲返还二分,即后一天返还的钱是前一天的二倍.问谁赢谁亏? 分析:数学建模
{an}:100 ,100 ,100……100 q=1
{bn}: 1 , 2 , 22 …… 229 q=2
S30 = 100+100+……+100 与 T30 = 1+2+ 22 +…… +229
比较大小 ,求和问题如何化简?
{an} : q=1,等比数列求和问题化归成等差数列求和问题
{bn} : q=2,如何求和?即:等比数列{an}一个数学游戏问题:探索等比数列求和公式 S1= a1
S2= a1 + a2 = a1+ a1q = a1( 1+q)
S3= a1 +a2 +a3 = a1+ a1q + a1q 2= a1( 1+q+ q2)
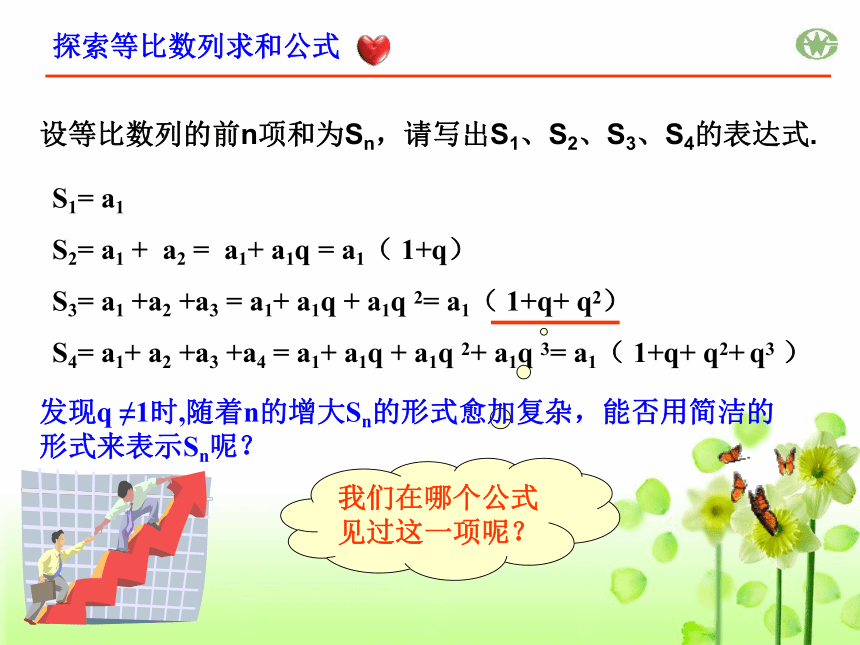
S4= a1+ a2 +a3 +a4 = a1+ a1q + a1q 2+ a1q 3= a1( 1+q+ q2+ q3 )设等比数列的前n项和为Sn,请写出S1、S2、S3、S4的表达式.我们在哪个公式见过这一项呢?发现q ≠1时,随着n的增大Sn的形式愈加复杂,能否用简洁的形式来表示Sn呢?探索等比数列求和公式在S3= a1( 1+q+ q2)的分子分母同乘以1-q (q ≠1)会得到什么结论?S1 、S2 、S4是否有同样的变形?动手动脑才是硬道理!探索等比数列求和公式猜想得:证明等比数列求和公式两边同乘以公比q错位相减法证明等比数列求和公式由此可得: 等比数列{an}前n项和 : 数学游戏问题答案:230–1 (分)=10737418. 23 (元)
远大于3000元证明等比数列求和公式公式的推导方法二:由等比数列的定义:根据等比的性质,有 即 :(结论同上)说明:围绕基本概念,从等比数列的定义出发,运用等比定理,导出了公式.典例精析例1:“棋盘上的麦粒”(以2为底的幂)历史典故
大家都见过国际象棋吧!它的棋盘是正四方形,黑白
相间共64格,传说在很久以前,古印度舍罕王在宫廷单调
的生活苦恼中,发现了也就是现今的国际象棋如此的有趣
和奥妙之后,决定要重赏发明人——他的宰相西萨班?达依
尔,让他随意选择奖品,宰相要求的赏赐是:在棋盘的第
一格内赏他一粒麦子,第二格内赏他两粒麦子,第三格四
粒麦子……以此类推每一格上的麦子数都是前一格的两
倍,国王一听,几粒麦子,加起来也不过一小袋,他就答
应了宰相的要求。实际国王能满足宰相的要求吗?典例精析分析:由 可得=18 446 744 073 709 551 615 (粒)人们估计,如果把这些麦粒依次排列,它的长度就相当于地球到太阳距离的2万倍。若按万粒400克计算,可达7000亿吨。而我国现年产量在4亿吨左右.∴国王不能实现他的诺言。 等比数列{ an}中
① a1= 8,an=0.5 , q=0.5 ,求Sn;
② a1= 2,S3= 26 , 求a3 , q;
③ a1=2 , S3=6 , 求q.练一练1:2:已知等比数列的前5项和为10,前10项和为50,求前15项和是多少?结论例2.某商场第一年销售计算机5000台,如果平均每年的销售量比上一年增加10%,那么从第一年起,约几年内可使总销售量达到30000台(保留到个位)?答:约5年内可以使总销售量达到30000台.典例精析本节课你有哪些收获?1、等比数列求和公式(注意分类讨论): 2、“错位相减法”求和。3、作业课本P69——1,2,3,4,5,6
{an}:100 ,100 ,100……100 q=1
{bn}: 1 , 2 , 22 …… 229 q=2
S30 = 100+100+……+100 与 T30 = 1+2+ 22 +…… +229
比较大小 ,求和问题如何化简?
{an} : q=1,等比数列求和问题化归成等差数列求和问题
{bn} : q=2,如何求和?即:等比数列{an}一个数学游戏问题:探索等比数列求和公式 S1= a1
S2= a1 + a2 = a1+ a1q = a1( 1+q)
S3= a1 +a2 +a3 = a1+ a1q + a1q 2= a1( 1+q+ q2)
S4= a1+ a2 +a3 +a4 = a1+ a1q + a1q 2+ a1q 3= a1( 1+q+ q2+ q3 )设等比数列的前n项和为Sn,请写出S1、S2、S3、S4的表达式.我们在哪个公式见过这一项呢?发现q ≠1时,随着n的增大Sn的形式愈加复杂,能否用简洁的形式来表示Sn呢?探索等比数列求和公式在S3= a1( 1+q+ q2)的分子分母同乘以1-q (q ≠1)会得到什么结论?S1 、S2 、S4是否有同样的变形?动手动脑才是硬道理!探索等比数列求和公式猜想得:证明等比数列求和公式两边同乘以公比q错位相减法证明等比数列求和公式由此可得: 等比数列{an}前n项和 : 数学游戏问题答案:230–1 (分)=10737418. 23 (元)
远大于3000元证明等比数列求和公式公式的推导方法二:由等比数列的定义:根据等比的性质,有 即 :(结论同上)说明:围绕基本概念,从等比数列的定义出发,运用等比定理,导出了公式.典例精析例1:“棋盘上的麦粒”(以2为底的幂)历史典故
大家都见过国际象棋吧!它的棋盘是正四方形,黑白
相间共64格,传说在很久以前,古印度舍罕王在宫廷单调
的生活苦恼中,发现了也就是现今的国际象棋如此的有趣
和奥妙之后,决定要重赏发明人——他的宰相西萨班?达依
尔,让他随意选择奖品,宰相要求的赏赐是:在棋盘的第
一格内赏他一粒麦子,第二格内赏他两粒麦子,第三格四
粒麦子……以此类推每一格上的麦子数都是前一格的两
倍,国王一听,几粒麦子,加起来也不过一小袋,他就答
应了宰相的要求。实际国王能满足宰相的要求吗?典例精析分析:由 可得=18 446 744 073 709 551 615 (粒)人们估计,如果把这些麦粒依次排列,它的长度就相当于地球到太阳距离的2万倍。若按万粒400克计算,可达7000亿吨。而我国现年产量在4亿吨左右.∴国王不能实现他的诺言。 等比数列{ an}中
① a1= 8,an=0.5 , q=0.5 ,求Sn;
② a1= 2,S3= 26 , 求a3 , q;
③ a1=2 , S3=6 , 求q.练一练1:2:已知等比数列的前5项和为10,前10项和为50,求前15项和是多少?结论例2.某商场第一年销售计算机5000台,如果平均每年的销售量比上一年增加10%,那么从第一年起,约几年内可使总销售量达到30000台(保留到个位)?答:约5年内可以使总销售量达到30000台.典例精析本节课你有哪些收获?1、等比数列求和公式(注意分类讨论): 2、“错位相减法”求和。3、作业课本P69——1,2,3,4,5,6
