小学数学人教版四年级上第八单元第2课时《烙饼问题》精品课件(共21张ppt)
文档属性
| 名称 | 小学数学人教版四年级上第八单元第2课时《烙饼问题》精品课件(共21张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-12 00:00:00 | ||
图片预览




文档简介
(共21张PPT)
烙饼问题
第八单元 数学广角——优化
学习目标
理解“烙饼问题”数学模型,掌握不同张数“烙饼”最优化方案的基本规律,能进行相关的简单实际应用。
认识到解决问题策略的多样性,培养解决问题最优方案的意识。
重点
输入标题
创设情境
谁见过妈妈烙饼?
妈妈每次是一张一张的烙的吗?
多张饼一起烙有什么好处?
你们爱吃饼吗?
输入标题
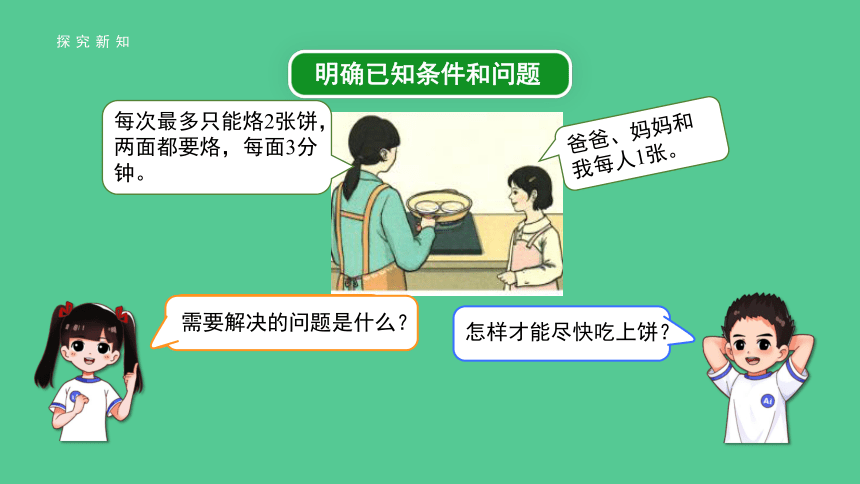
明确已知条件和问题
你能得到哪些信息?
探究新知
爸爸、妈妈和我每人1张。
每次最多只能烙2张饼,两面都要烙,每面3分钟。
需要解决的问题是什么?
怎样才能尽快吃上饼?
输入标题
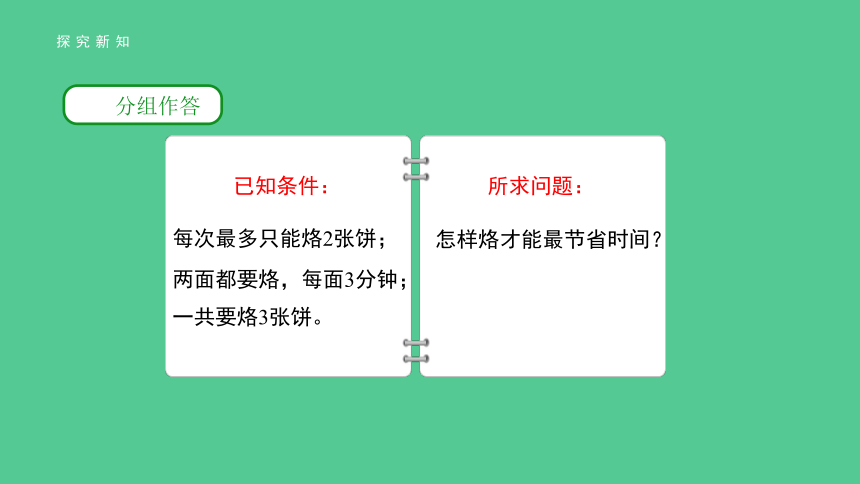
已知条件:
所求问题:
每次最多只能烙2张饼;
两面都要烙,每面3分钟;
一共要烙3张饼。
怎样烙才能最节省时间?
探究新知
分组作答
输入标题
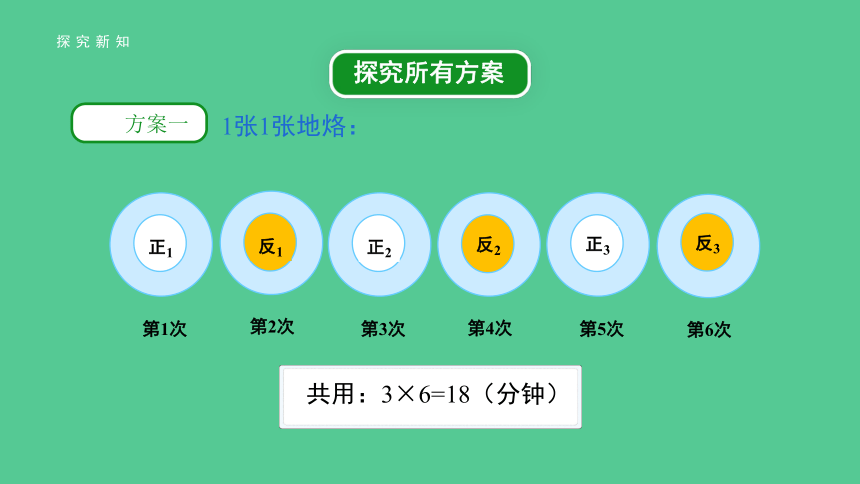
1张1张地烙:
共用:3×6=18(分钟)
第2次
反1
第3次
正2
第4次
反2
第5次
正3
第6次
反3
第1次
正1
探究新知
探究所有方案
方案一
输入标题
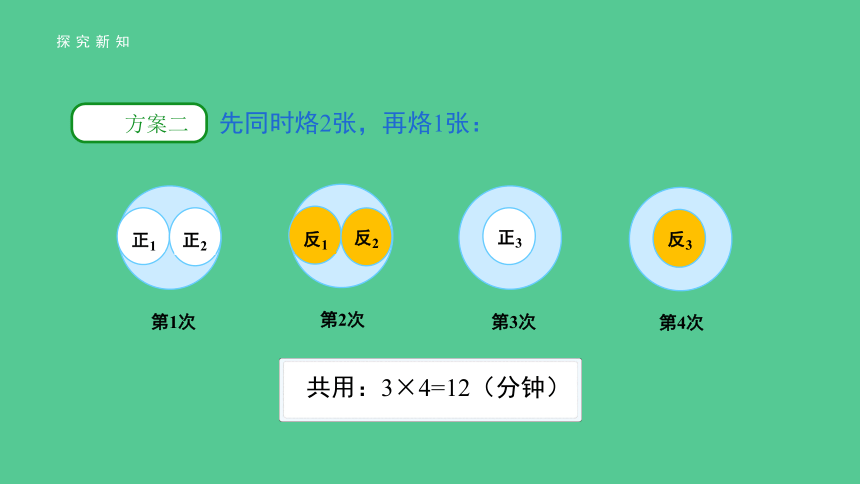
先同时烙2张,再烙1张:
共用:3×4=12(分钟)
第2次
反1
反2
第3次
正3
第4次
反3
第1次
正1
正2
探究新知
方案二
输入标题
保证锅中每次都有2张饼:
共用:3×3=9(分钟)
第2次
反1
正3
第1次
正1
正2
第3次
反3
反2
探究新知
方案三
输入标题
共用:3×6=18(分钟)
共用:3×4=12(分钟)
方案一
1张1张地烙:
方案二
先同时烙2张,再烙1张:
共用:3×3=9(分钟)
方案三
保证锅中每次都有2张饼:
探究新知
对比得出最优方案
最优方案
最优方案
输入标题
比较发现:每次总烙2张饼,别让锅有空余,这样最省时间。
这是烙饼问题最省时间的关键!
探究新知
输入标题
已知条件:
所求问题:
每次最多只能烙2张饼;
两面都要烙,每面3分钟;
如果要烙1张、2张呢,怎样烙才能最节省时间?
探究新知
进一步探究烙饼问题
分组作答
输入标题
探究新知
烙2张饼最节省时间的方法是2张一起烙,共需:3×2=6(分钟)。
烙1张饼只有一种方法。
对,只能一面一面地烙,共需:3×2=6(分钟)。
输入标题
已知条件:
所求问题:
每次最多只能烙2张饼;
两面都要烙,每面3分钟;
如果要烙4张、5张、6张……呢,怎样烙才能最节省时间?
探究新知
分组作答
输入标题
烙饼张数 烙饼的方法 次数 所需最短时间(分钟)
2
3
2张一起烙
保证锅中每次都有2张饼
2
3
3×2=6
3×3=9
4
5
6
7
8
9
10
……
2张2张地烙
先烙2张,后3张用方案三烙
2张2张地烙
先2张2张地烙,后3张用方案三烙
2张2张地烙
先2张2张地烙,后3张用方案三烙
2张2张地烙
……
4
5
6
7
8
9
10
……
3×4=12
3×5=15
3×6=18
3×7=21
3×8=24
3×9=27
3×10=30
……
探究新知
输入标题
规律:要烙的饼的张数如果是双数,2张2张地烙就可以;如果是单数,可以先2张2张地烙,最后3张按“烙3张饼”的最优方案去烙,最节省时间。
探究新知
输入标题
小结
烙饼问题的最优方案是每次尽可能地让锅里按要求放最多的饼,这样既不浪费资源,又节省时间。
探究新知
输入标题
1.一件木雕工艺品两面都要雕(同一件的两面不能同时雕),一位工人雕一面要8小时,2位工人共雕3件工艺品最少要多少小时?
3×8=24(小时)
答:3件艺术品分别记为a、b、c,第一次雕a、b的正面,第二次雕a的反面和c的正面,第三次雕b、c的反面。最少要24小时。
巩固练习
输入标题
2.牛牛、丁丁、田田三人过桥,桥上每次只能走两个人,每人过桥后再返回需要2分钟(往返各需1分钟),三人过桥后再返回一共至少需要多少分钟?
1×3=3(分钟)
答:第1分钟牛牛、丁丁过去;第2分钟牛牛回来,田田过去;第3分钟丁丁、田田回来,所以至少需要3分钟。
巩固练习
输入标题
3.鱼的两面都要煎,锅里一次最多可以放4条鱼,每煎一面要5分钟。煎6条鱼至少要多少分钟?
3×5=15(分钟)
答:6条鱼分别记为a、b、c、d、e、f,第一次煎a、b、c、d的正面,第二次煎a、b的反面和e、f的正面,第三次煎c、d、e、f的反面。最少需要15分钟。
巩固练习
课堂小结
今天的学习你有什么收获?
1.我不仅会解答烙饼问题了;
2.还学会了如何解答同类型的其他题目。
再见
烙饼问题
第八单元 数学广角——优化
学习目标
理解“烙饼问题”数学模型,掌握不同张数“烙饼”最优化方案的基本规律,能进行相关的简单实际应用。
认识到解决问题策略的多样性,培养解决问题最优方案的意识。
重点
输入标题
创设情境
谁见过妈妈烙饼?
妈妈每次是一张一张的烙的吗?
多张饼一起烙有什么好处?
你们爱吃饼吗?
输入标题
明确已知条件和问题
你能得到哪些信息?
探究新知
爸爸、妈妈和我每人1张。
每次最多只能烙2张饼,两面都要烙,每面3分钟。
需要解决的问题是什么?
怎样才能尽快吃上饼?
输入标题
已知条件:
所求问题:
每次最多只能烙2张饼;
两面都要烙,每面3分钟;
一共要烙3张饼。
怎样烙才能最节省时间?
探究新知
分组作答
输入标题
1张1张地烙:
共用:3×6=18(分钟)
第2次
反1
第3次
正2
第4次
反2
第5次
正3
第6次
反3
第1次
正1
探究新知
探究所有方案
方案一
输入标题
先同时烙2张,再烙1张:
共用:3×4=12(分钟)
第2次
反1
反2
第3次
正3
第4次
反3
第1次
正1
正2
探究新知
方案二
输入标题
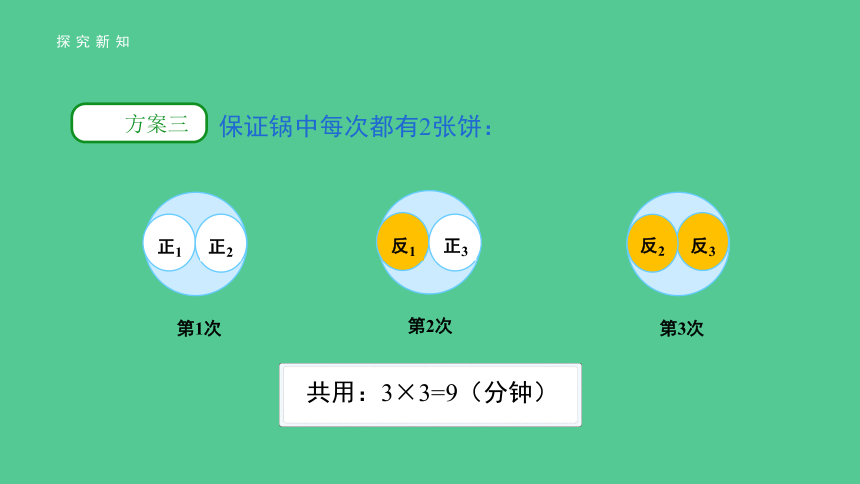
保证锅中每次都有2张饼:
共用:3×3=9(分钟)
第2次
反1
正3
第1次
正1
正2
第3次
反3
反2
探究新知
方案三
输入标题
共用:3×6=18(分钟)
共用:3×4=12(分钟)
方案一
1张1张地烙:
方案二
先同时烙2张,再烙1张:
共用:3×3=9(分钟)
方案三
保证锅中每次都有2张饼:
探究新知
对比得出最优方案
最优方案
最优方案
输入标题
比较发现:每次总烙2张饼,别让锅有空余,这样最省时间。
这是烙饼问题最省时间的关键!
探究新知
输入标题
已知条件:
所求问题:
每次最多只能烙2张饼;
两面都要烙,每面3分钟;
如果要烙1张、2张呢,怎样烙才能最节省时间?
探究新知
进一步探究烙饼问题
分组作答
输入标题
探究新知
烙2张饼最节省时间的方法是2张一起烙,共需:3×2=6(分钟)。
烙1张饼只有一种方法。
对,只能一面一面地烙,共需:3×2=6(分钟)。
输入标题
已知条件:
所求问题:
每次最多只能烙2张饼;
两面都要烙,每面3分钟;
如果要烙4张、5张、6张……呢,怎样烙才能最节省时间?
探究新知
分组作答
输入标题
烙饼张数 烙饼的方法 次数 所需最短时间(分钟)
2
3
2张一起烙
保证锅中每次都有2张饼
2
3
3×2=6
3×3=9
4
5
6
7
8
9
10
……
2张2张地烙
先烙2张,后3张用方案三烙
2张2张地烙
先2张2张地烙,后3张用方案三烙
2张2张地烙
先2张2张地烙,后3张用方案三烙
2张2张地烙
……
4
5
6
7
8
9
10
……
3×4=12
3×5=15
3×6=18
3×7=21
3×8=24
3×9=27
3×10=30
……
探究新知
输入标题
规律:要烙的饼的张数如果是双数,2张2张地烙就可以;如果是单数,可以先2张2张地烙,最后3张按“烙3张饼”的最优方案去烙,最节省时间。
探究新知
输入标题
小结
烙饼问题的最优方案是每次尽可能地让锅里按要求放最多的饼,这样既不浪费资源,又节省时间。
探究新知
输入标题
1.一件木雕工艺品两面都要雕(同一件的两面不能同时雕),一位工人雕一面要8小时,2位工人共雕3件工艺品最少要多少小时?
3×8=24(小时)
答:3件艺术品分别记为a、b、c,第一次雕a、b的正面,第二次雕a的反面和c的正面,第三次雕b、c的反面。最少要24小时。
巩固练习
输入标题
2.牛牛、丁丁、田田三人过桥,桥上每次只能走两个人,每人过桥后再返回需要2分钟(往返各需1分钟),三人过桥后再返回一共至少需要多少分钟?
1×3=3(分钟)
答:第1分钟牛牛、丁丁过去;第2分钟牛牛回来,田田过去;第3分钟丁丁、田田回来,所以至少需要3分钟。
巩固练习
输入标题
3.鱼的两面都要煎,锅里一次最多可以放4条鱼,每煎一面要5分钟。煎6条鱼至少要多少分钟?
3×5=15(分钟)
答:6条鱼分别记为a、b、c、d、e、f,第一次煎a、b、c、d的正面,第二次煎a、b的反面和e、f的正面,第三次煎c、d、e、f的反面。最少需要15分钟。
巩固练习
课堂小结
今天的学习你有什么收获?
1.我不仅会解答烙饼问题了;
2.还学会了如何解答同类型的其他题目。
再见
