1.1.1棱柱、棱锥、棱台的结构特征 课件(共44张PPT)
文档属性
| 名称 | 1.1.1棱柱、棱锥、棱台的结构特征 课件(共44张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-13 06:56:39 | ||
图片预览







文档简介
(共44张PPT)
数 学
必修② · 人教A版
新课标导学
第一章
空间几何体
1.1 空间几何体的结构
1.1.1 棱柱、棱锥、棱台的结构特征
1
自主预习学案
2
互动探究学案
3
课时作业学案
自主预习学案
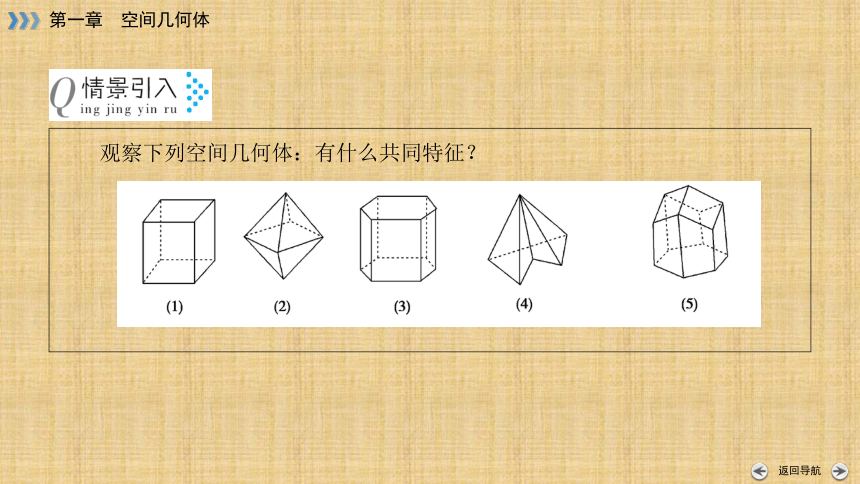
观察下列空间几何体:有什么共同特征?
一、空间几何体
1.概念:如果只考虑物体的_______和______,而不考虑其他因素,那么由这些物体抽象出来的_________叫做空间几何体.
2.多面体与旋转体
(1)多面体:由若干个____________围成的几何体叫做多面体(如图),围成多面体的各个多边形叫做多面体的____;相邻两个面的__________叫做多面体的棱;棱与棱的________叫做多面体的顶点.
(2)旋转体:我们把由一个平面图形绕它所在平面内的一条定_______旋转所形成的______________叫做旋转体,这条定直线叫做旋转体的轴.
形状
大小
空间图形
平面多边形
面
公共边
公共点
直线
封闭几何体
[归纳总结] 对多面体概念的理解,注意以下几个方面:
(1)多面体是由平面多边形围成的,不是由圆面或其它曲面围成,也不是由空间多边形围成.
(2)本章所说的多边形,一般包括它内部的平面部分,故多面体是一个“封闭”的几何体.
(3)围成一个多面体至少要有四个面.
(4)规定:在多面体中,不在同一面上的两个顶点的连线叫做多面体的对角线,不在同一面上的两条侧棱称为多面体的不相邻侧棱,侧棱和底面多边形的边统称为棱.
(5)一个多面体是由几个面围成,那么这个多面体称为几面体.
二、几种常见的多面体
1.棱柱
定义 一般地,有两个面互相_______,其余各面都是_________,并且每________两个四边形的公共边都互相______,由这些面所围成的_________叫做棱柱
有关
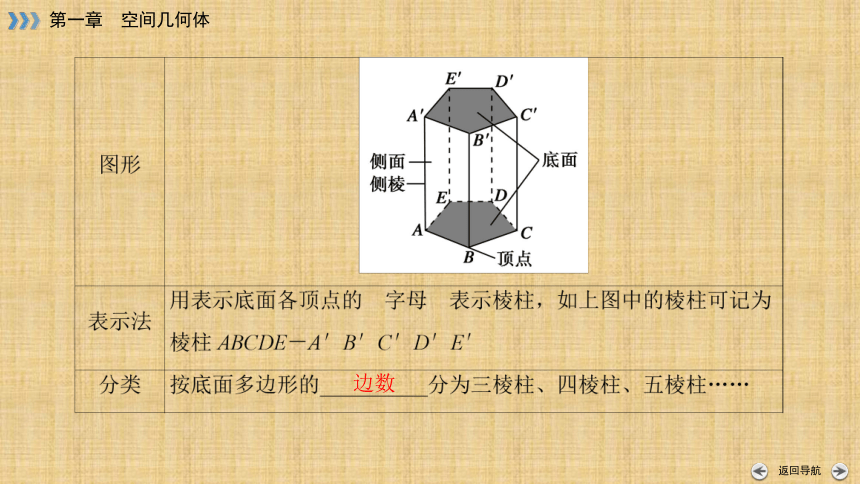
概念 棱柱中,两个互相_______的面叫做棱柱的底面,简称底;其余各面叫做棱柱的侧面;相邻侧面的__________叫做棱柱的侧棱;侧面与底面的____________叫做棱柱的顶点
平行
四边形
相邻
平行
多面体
平行
公共边
公共顶点
边数
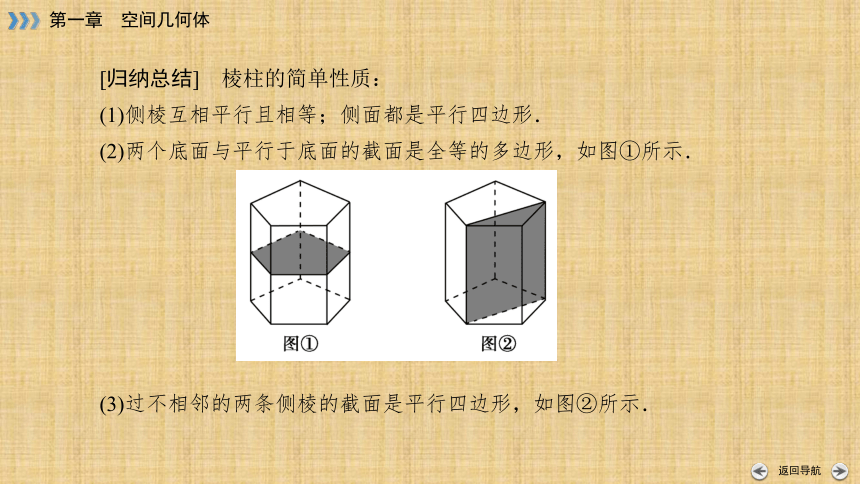
[归纳总结] 棱柱的简单性质:
(1)侧棱互相平行且相等;侧面都是平行四边形.
(2)两个底面与平行于底面的截面是全等的多边形,如图①所示.
(3)过不相邻的两条侧棱的截面是平行四边形,如图②所示.
棱柱概念的推广
(1)斜棱柱:侧棱不垂直于底面的棱柱叫做斜棱柱.
(2)直棱柱:侧棱垂直于底面的棱柱叫做直棱柱.
(3)正棱柱:底面是正多边形的直棱柱叫做正棱柱.
(4)平面六面体:底面是平行四边形的四棱柱叫做平行六面体,即平行六面体的六个面都是平行四边形.
(5)长方体:底面是矩形的直棱柱叫做长方体.
(6)正方体:棱长都相等的长方体叫做正方体.
2.棱锥
定义 一般地,有一个面是___________,其余各面都是________________的三角形,由这些面所围成的多面体叫做棱锥
有关
概念 多边形面叫做棱锥的底面或底;有_____________的各个三角形面叫做棱锥的侧面;各侧面的_____________叫做棱锥的顶点;相邻侧面的_____________叫做棱锥的侧棱
多边形
有一个公共顶点
公共顶点
公共顶点
公共边
字母
S-ABCD
边数
四面体
[归纳总结] 棱锥的性质:
(1)侧棱有公共点,即棱锥的顶点;侧面都是三角形.
(2)底面与平行于底面的截面是相似多边形,如图①所示.
(3)过不相邻的两条侧棱的截面是三角形,如图②所示.
3.棱台
定义 用一个_____________棱锥底面的平面去截棱锥,____________之间的部分叫做棱台
有关
概念 原棱锥的底面和截面分别叫做棱台的____________和__________;其它各面叫做棱台的____________;相邻侧面的____________叫做棱台的侧棱;底面与____________的公共顶点叫做棱台的顶点
平行于
底面与截面
下底面
上底面
侧面
公共边
侧面
ABCD-A′B′C′D′
边数
[归纳总结] 棱台的性质:
(1)侧棱延长后交于一点;侧面是梯形.
(2)两个底面与平行于底面的截面是相似多边形,如图①所示.
(3)过不相邻的两条侧棱的截面是梯形,如图②所示.
[解析] 水立方是多面体,不能抽象成旋转体;篮球、日光灯管、电线杆都可抽象成旋转体.
D
[解析] 根据棱锥顶点的定义可知,四棱锥只有一个顶点,故选项B不正确.
B
[解析] 三棱锥的侧面和底面均是三角形,故选A.
A
4
8
互动探究学案
命题方向1 棱柱的结构特征
(3)(4)
[思路分析] 首先看是否有两个平行的面作为底面,再看是否满足其他性质.
[解析] (1)错误,棱柱的底面不一定是平行四边形;
(2)错误,棱柱的底面可以是三角形;
(3)正确,由棱柱的定义易知;
(4)正确,棱柱可以被平行于底面的平面截成两个棱柱,
所以说法正确的序号是(3)(4).
『规律方法』 (1)紧扣棱柱的结构特征进行有关概念辨析
①两个面互相平行;
②其余各面是四边形;
③相邻两个四边形的公共边互相平行.
(2)多注意观察一些实物模型和图片便于反例排除.
[解析] 由棱柱的定义知,棱柱的侧面都是平行四边形,不一定都是矩形,故A不正确;而平行四边形的对边相等,故侧棱都相等,所以B正确;对选项C,侧棱都平行,但底面多边形的边(也是棱)不一定平行,所以错误;棱柱的侧棱可以与底面垂直也可以不与底面垂直,故D不正确.
B
命题方向2 棱锥、棱台的结构特征
[思路分析] 根据棱锥、棱台的结构特征进行判断.
(1)(2)(3)
[解析] (1)正确,棱台的侧面都是梯形.
(2)正确,由棱锥的定义知棱锥的侧面只能是三角形.
(3)正确,由四个面围成的封闭图形只能是三棱锥.
(4)错误,如(右)图所示四棱锥被平面截成的两部分都是棱锥.
『规律方法』 关于棱锥、棱台结构特征题目的判断方法:
(1)举反例法
结合棱锥、棱台的定义举反例直接判断关于棱锥、棱台结构特征的某些说法不正确.
(2)直接法
棱锥 棱台
定底面 只有一个面是多边形,此面即为底面 两个互相平行的面,即为底面
看侧棱 相交于一点 延长后相交于一点
[解析] 图①、②、③都不是棱台.因为图①和图③都不是由棱锥所截得的,故图①、③都不是棱台,虽然图②是由棱锥所截得的,但截面不和底面平行,故不是棱台,只有用平行于棱锥底面的平面去截棱锥,底面与截面之间的部分才是棱台.
对棱柱、棱锥、棱台的概念理解不透
[错解] 一定是棱柱.
[错因分析] 棱柱的定义:有两个面互相平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行,这些面围成的几何体叫做棱柱.题中漏掉了“并且每相邻两个四边形的公共边都互相平行”这一条件,因此所围成的几何体可能不是棱柱.
[正解] 满足题目条件的几何体不一定是棱柱,如图所示的几何体满足题中条件,但都不是棱柱.
[错解] 对
[辨析] 判断几何体的形状,一定要紧扣几何体的定义,在棱锥的定义中,“有一个公共顶点”的条件不可缺少.
[答案] 错误.棱锥的正确定义是“有一个面是多边形,其余各面是有一个公共顶点的三角形.由这些面所围成的几何体叫做棱锥.”
空间想象能力与几何体的侧面展开
空间想象能力,立体几何学习的一个核心任务就是培养空间想象能力,学习过程中可通过以下方式提升空间想象能力.
(1)借助周围空间中的几何体和动手制作直观教具,作为直观支柱帮助建立空间观念;(2)加强作图和识图能力培养;(3)加强几何语言与图形、文字语言的转换训练;(4)注意平面几何知识与立体几何知识的沟通与区分;(5)注重训练推理语言的规范性;(6)借助可能的多媒体展示,培养直观想象能力.
[思路分析] 由题目可获取以下主要信息:
(1)都是多面体;(2)①中的折痕是平行线,是棱柱;
②中折痕交于一点,是棱锥;
③中侧面是梯形,是棱台.
『规律方法』 立体图形的展开或平面图形的折叠是培养空间想象能力的有效途径,解此类问题可以结合常见几何体的定义与结构特征,进行空间想象,或亲自动手制作平面展开图进行实践.
B
[解析] 将所给图形还原为正方体,如图3所示,最上面为△,最左面为东,最里面为上,将正方体旋转后让左面向东,让“上”面向上可知“△”的方位为北.
[解析] 棱柱的侧棱互相平行且相等,故选C.
C
[解析] 棱锥的任意两个面都相交,不可能有两个面平行,所以不可能是棱锥.
B
A
[解析] 面数最少的棱台是三棱台,共有5个面,6个顶点,9条棱.
5
6
9
D
课时作业学案
数 学
必修② · 人教A版
新课标导学
第一章
空间几何体
1.1 空间几何体的结构
1.1.1 棱柱、棱锥、棱台的结构特征
1
自主预习学案
2
互动探究学案
3
课时作业学案
自主预习学案
观察下列空间几何体:有什么共同特征?
一、空间几何体
1.概念:如果只考虑物体的_______和______,而不考虑其他因素,那么由这些物体抽象出来的_________叫做空间几何体.
2.多面体与旋转体
(1)多面体:由若干个____________围成的几何体叫做多面体(如图),围成多面体的各个多边形叫做多面体的____;相邻两个面的__________叫做多面体的棱;棱与棱的________叫做多面体的顶点.
(2)旋转体:我们把由一个平面图形绕它所在平面内的一条定_______旋转所形成的______________叫做旋转体,这条定直线叫做旋转体的轴.
形状
大小
空间图形
平面多边形
面
公共边
公共点
直线
封闭几何体
[归纳总结] 对多面体概念的理解,注意以下几个方面:
(1)多面体是由平面多边形围成的,不是由圆面或其它曲面围成,也不是由空间多边形围成.
(2)本章所说的多边形,一般包括它内部的平面部分,故多面体是一个“封闭”的几何体.
(3)围成一个多面体至少要有四个面.
(4)规定:在多面体中,不在同一面上的两个顶点的连线叫做多面体的对角线,不在同一面上的两条侧棱称为多面体的不相邻侧棱,侧棱和底面多边形的边统称为棱.
(5)一个多面体是由几个面围成,那么这个多面体称为几面体.
二、几种常见的多面体
1.棱柱
定义 一般地,有两个面互相_______,其余各面都是_________,并且每________两个四边形的公共边都互相______,由这些面所围成的_________叫做棱柱
有关
概念 棱柱中,两个互相_______的面叫做棱柱的底面,简称底;其余各面叫做棱柱的侧面;相邻侧面的__________叫做棱柱的侧棱;侧面与底面的____________叫做棱柱的顶点
平行
四边形
相邻
平行
多面体
平行
公共边
公共顶点
边数
[归纳总结] 棱柱的简单性质:
(1)侧棱互相平行且相等;侧面都是平行四边形.
(2)两个底面与平行于底面的截面是全等的多边形,如图①所示.
(3)过不相邻的两条侧棱的截面是平行四边形,如图②所示.
棱柱概念的推广
(1)斜棱柱:侧棱不垂直于底面的棱柱叫做斜棱柱.
(2)直棱柱:侧棱垂直于底面的棱柱叫做直棱柱.
(3)正棱柱:底面是正多边形的直棱柱叫做正棱柱.
(4)平面六面体:底面是平行四边形的四棱柱叫做平行六面体,即平行六面体的六个面都是平行四边形.
(5)长方体:底面是矩形的直棱柱叫做长方体.
(6)正方体:棱长都相等的长方体叫做正方体.
2.棱锥
定义 一般地,有一个面是___________,其余各面都是________________的三角形,由这些面所围成的多面体叫做棱锥
有关
概念 多边形面叫做棱锥的底面或底;有_____________的各个三角形面叫做棱锥的侧面;各侧面的_____________叫做棱锥的顶点;相邻侧面的_____________叫做棱锥的侧棱
多边形
有一个公共顶点
公共顶点
公共顶点
公共边
字母
S-ABCD
边数
四面体
[归纳总结] 棱锥的性质:
(1)侧棱有公共点,即棱锥的顶点;侧面都是三角形.
(2)底面与平行于底面的截面是相似多边形,如图①所示.
(3)过不相邻的两条侧棱的截面是三角形,如图②所示.
3.棱台
定义 用一个_____________棱锥底面的平面去截棱锥,____________之间的部分叫做棱台
有关
概念 原棱锥的底面和截面分别叫做棱台的____________和__________;其它各面叫做棱台的____________;相邻侧面的____________叫做棱台的侧棱;底面与____________的公共顶点叫做棱台的顶点
平行于
底面与截面
下底面
上底面
侧面
公共边
侧面
ABCD-A′B′C′D′
边数
[归纳总结] 棱台的性质:
(1)侧棱延长后交于一点;侧面是梯形.
(2)两个底面与平行于底面的截面是相似多边形,如图①所示.
(3)过不相邻的两条侧棱的截面是梯形,如图②所示.
[解析] 水立方是多面体,不能抽象成旋转体;篮球、日光灯管、电线杆都可抽象成旋转体.
D
[解析] 根据棱锥顶点的定义可知,四棱锥只有一个顶点,故选项B不正确.
B
[解析] 三棱锥的侧面和底面均是三角形,故选A.
A
4
8
互动探究学案
命题方向1 棱柱的结构特征
(3)(4)
[思路分析] 首先看是否有两个平行的面作为底面,再看是否满足其他性质.
[解析] (1)错误,棱柱的底面不一定是平行四边形;
(2)错误,棱柱的底面可以是三角形;
(3)正确,由棱柱的定义易知;
(4)正确,棱柱可以被平行于底面的平面截成两个棱柱,
所以说法正确的序号是(3)(4).
『规律方法』 (1)紧扣棱柱的结构特征进行有关概念辨析
①两个面互相平行;
②其余各面是四边形;
③相邻两个四边形的公共边互相平行.
(2)多注意观察一些实物模型和图片便于反例排除.
[解析] 由棱柱的定义知,棱柱的侧面都是平行四边形,不一定都是矩形,故A不正确;而平行四边形的对边相等,故侧棱都相等,所以B正确;对选项C,侧棱都平行,但底面多边形的边(也是棱)不一定平行,所以错误;棱柱的侧棱可以与底面垂直也可以不与底面垂直,故D不正确.
B
命题方向2 棱锥、棱台的结构特征
[思路分析] 根据棱锥、棱台的结构特征进行判断.
(1)(2)(3)
[解析] (1)正确,棱台的侧面都是梯形.
(2)正确,由棱锥的定义知棱锥的侧面只能是三角形.
(3)正确,由四个面围成的封闭图形只能是三棱锥.
(4)错误,如(右)图所示四棱锥被平面截成的两部分都是棱锥.
『规律方法』 关于棱锥、棱台结构特征题目的判断方法:
(1)举反例法
结合棱锥、棱台的定义举反例直接判断关于棱锥、棱台结构特征的某些说法不正确.
(2)直接法
棱锥 棱台
定底面 只有一个面是多边形,此面即为底面 两个互相平行的面,即为底面
看侧棱 相交于一点 延长后相交于一点
[解析] 图①、②、③都不是棱台.因为图①和图③都不是由棱锥所截得的,故图①、③都不是棱台,虽然图②是由棱锥所截得的,但截面不和底面平行,故不是棱台,只有用平行于棱锥底面的平面去截棱锥,底面与截面之间的部分才是棱台.
对棱柱、棱锥、棱台的概念理解不透
[错解] 一定是棱柱.
[错因分析] 棱柱的定义:有两个面互相平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行,这些面围成的几何体叫做棱柱.题中漏掉了“并且每相邻两个四边形的公共边都互相平行”这一条件,因此所围成的几何体可能不是棱柱.
[正解] 满足题目条件的几何体不一定是棱柱,如图所示的几何体满足题中条件,但都不是棱柱.
[错解] 对
[辨析] 判断几何体的形状,一定要紧扣几何体的定义,在棱锥的定义中,“有一个公共顶点”的条件不可缺少.
[答案] 错误.棱锥的正确定义是“有一个面是多边形,其余各面是有一个公共顶点的三角形.由这些面所围成的几何体叫做棱锥.”
空间想象能力与几何体的侧面展开
空间想象能力,立体几何学习的一个核心任务就是培养空间想象能力,学习过程中可通过以下方式提升空间想象能力.
(1)借助周围空间中的几何体和动手制作直观教具,作为直观支柱帮助建立空间观念;(2)加强作图和识图能力培养;(3)加强几何语言与图形、文字语言的转换训练;(4)注意平面几何知识与立体几何知识的沟通与区分;(5)注重训练推理语言的规范性;(6)借助可能的多媒体展示,培养直观想象能力.
[思路分析] 由题目可获取以下主要信息:
(1)都是多面体;(2)①中的折痕是平行线,是棱柱;
②中折痕交于一点,是棱锥;
③中侧面是梯形,是棱台.
『规律方法』 立体图形的展开或平面图形的折叠是培养空间想象能力的有效途径,解此类问题可以结合常见几何体的定义与结构特征,进行空间想象,或亲自动手制作平面展开图进行实践.
B
[解析] 将所给图形还原为正方体,如图3所示,最上面为△,最左面为东,最里面为上,将正方体旋转后让左面向东,让“上”面向上可知“△”的方位为北.
[解析] 棱柱的侧棱互相平行且相等,故选C.
C
[解析] 棱锥的任意两个面都相交,不可能有两个面平行,所以不可能是棱锥.
B
A
[解析] 面数最少的棱台是三棱台,共有5个面,6个顶点,9条棱.
5
6
9
D
课时作业学案
