18.2.1 矩形 课后练习(含答案)人教版八年级下册
文档属性
| 名称 | 18.2.1 矩形 课后练习(含答案)人教版八年级下册 |  | |
| 格式 | zip | ||
| 文件大小 | 422.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-13 20:32:23 | ||
图片预览

文档简介
18.2.1矩形 课后练习
一、单选题
1.在四边形ABCD中,对角线AC,BD互相平分,要使四边形ABCD为矩形,需添加的条件是( )
A.∠A=∠C B.AB=BC C.AC⊥BD D.AC=BD
2.要检验一个四边形的桌面是否为矩形,可行的测量方案是( )
A.测量两条对角线是否相等
B.度量两个角是否是90°
C.测量两条对角线的交点到四个顶点的距离是否相等
D.测量两组对边是否分别相等
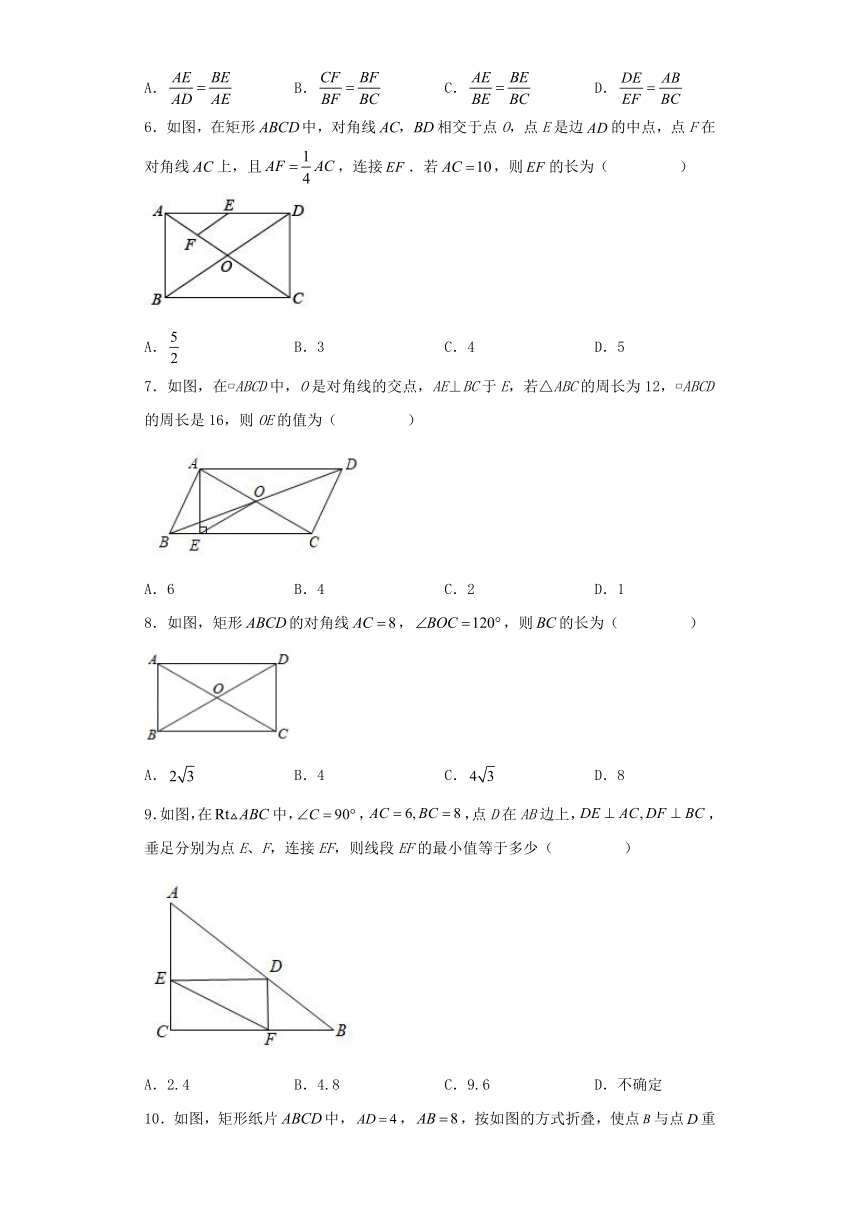
3.如图,在矩形中,,,点E在边上,若平分,则的长为( )
A. B. C. D.
4.如图,在矩形ABCD中,对角线AC、BD相交于点O,交BD于点E,,则的度数为( )
A.40° B.35° C.30° D.25°
5.我们把宽与长的比等于黄金比的矩形称为黄金矩形.如图,在黄金矩形中,的平分线交边于点,于点,则下列结论错误的是( )
A. B. C. D.
6.如图,在矩形中,对角线相交于点O,点E是边的中点,点F在对角线上,且,连接.若,则的长为( )
A. B.3 C.4 D.5
7.如图,在 ABCD中,O是对角线的交点,AE⊥BC于E,若△ABC的周长为12, ABCD的周长是16,则OE的值为( )
A.6 B.4 C.2 D.1
8.如图,矩形的对角线,,则的长为( )
A. B.4 C. D.8
9.如图,在中,,,点D在AB边上,,垂足分别为点E、F,连接EF,则线段EF的最小值等于多少( )
A.2.4 B.4.8 C.9.6 D.不确定
10.如图,矩形纸片中,,,按如图的方式折叠,使点与点重合,则折痕的长为( )
A. B. C. D.
二、填空题
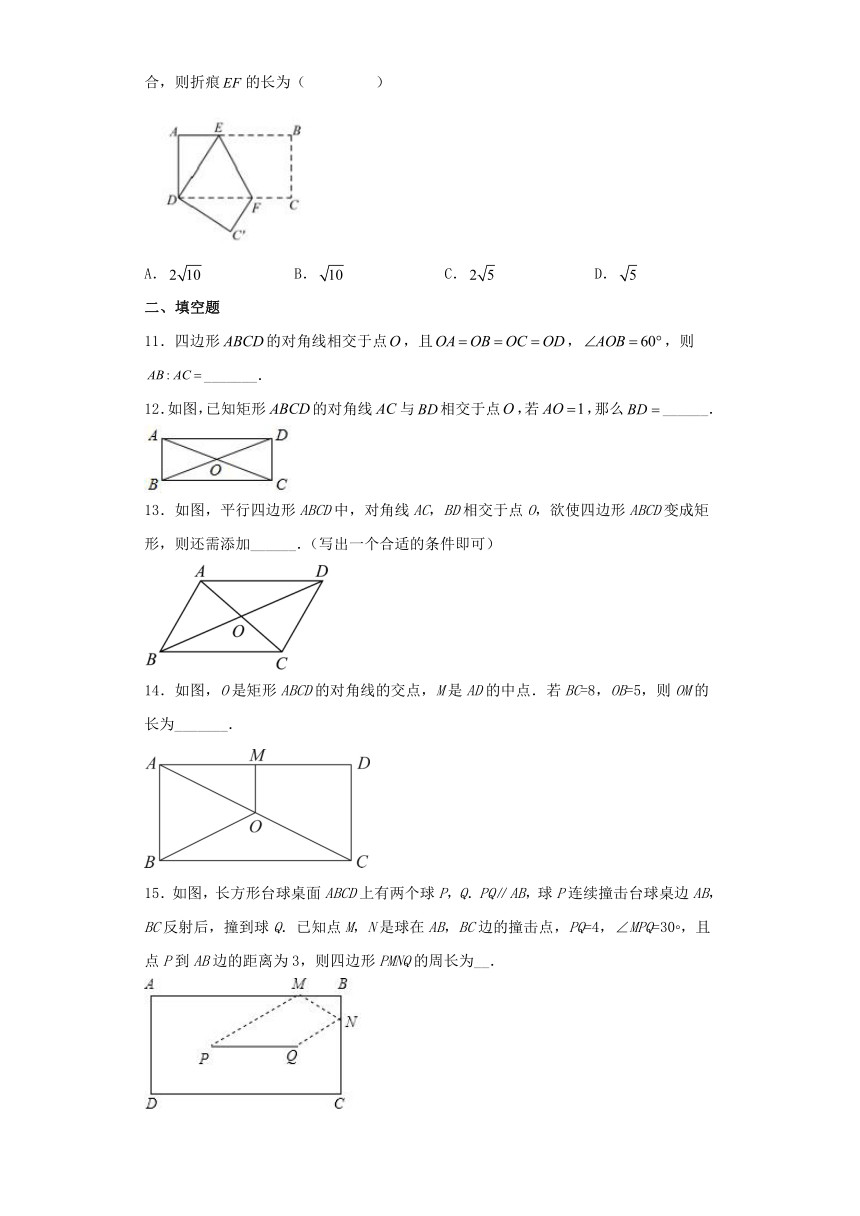
11.四边形的对角线相交于点,且,,则_______.
12.如图,已知矩形的对角线与相交于点,若,那么______.
13.如图,平行四边形ABCD中,对角线AC,BD相交于点O,欲使四边形ABCD变成矩形,则还需添加______.(写出一个合适的条件即可)
14.如图,O是矩形ABCD的对角线的交点,M是AD的中点.若BC=8,OB=5,则OM的长为_______.
15.如图,长方形台球桌面ABCD上有两个球P,Q.PQ∥AB,球P连续撞击台球桌边AB,BC反射后,撞到球Q.已知点M,N是球在AB,BC边的撞击点,PQ=4,∠MPQ=30 ,且点P到AB边的距离为3,则四边形PMNQ的周长为__.
三、解答题
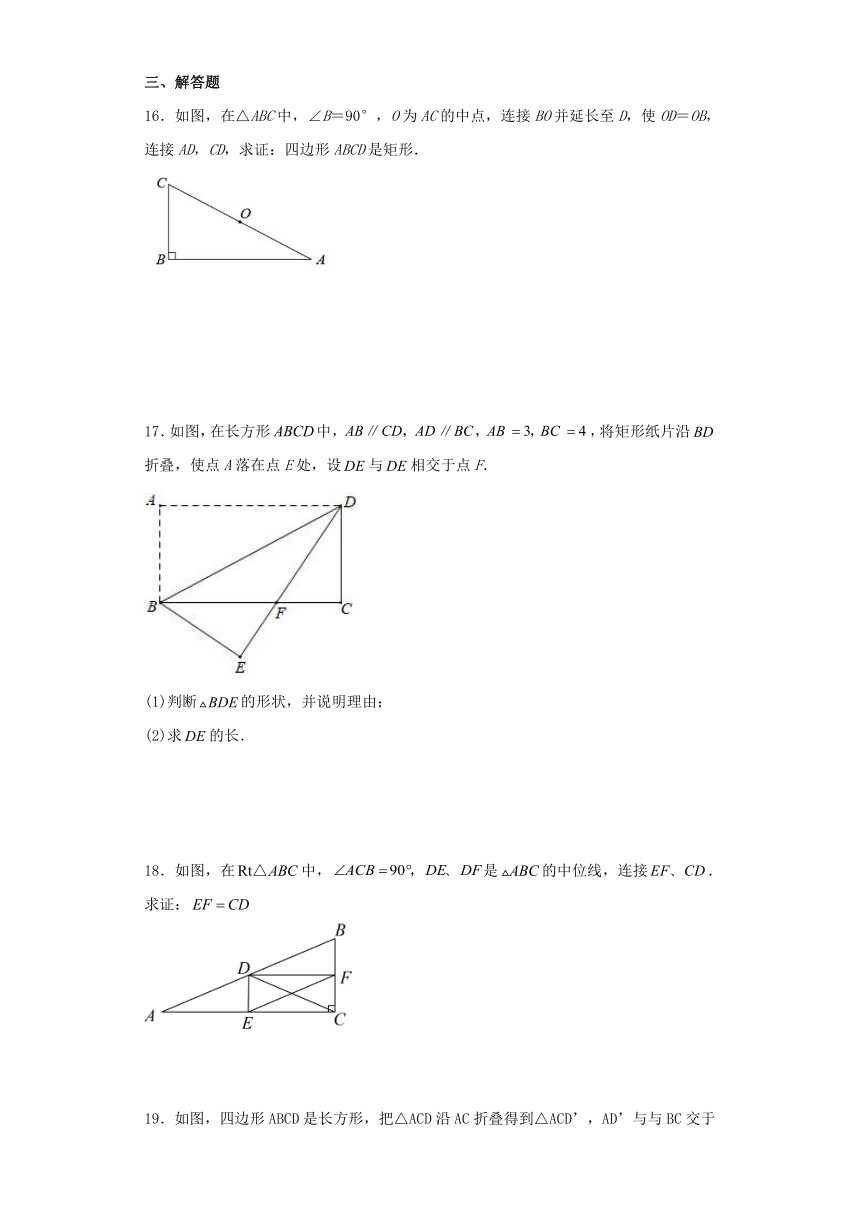
16.如图,在△ABC中,∠B=90°,O为AC的中点,连接BO并延长至D,使OD=OB,连接AD,CD,求证:四边形ABCD是矩形.
17.如图,在长方形中,,将矩形纸片沿折叠,使点A落在点E处,设与相交于点F.
(1)判断的形状,并说明理由;
(2)求的长.
18.如图,在中,是的中位线,连接.
求证:
19.如图,四边形ABCD是长方形,把△ACD沿AC折叠得到△ACD’,AD’与与BC交于点E,若AD=4,DC=3
(1)求证
(2)求BE的长
20.如图,在长方形纸片中,,将纸片折叠压平,使点与点重合,折痕为.
(1)求证:.
(2)求线段的长.
参考答案
1.D
2.C
3.C
4.B
5.C
6.A
7.C
8.C
9.B
10.C
11.1:2
12.2
13.AC=BD(答案不唯一)
14.3
15.16.
16.证明:如图,
∵O为AC的中点,
∴ ,
∵ ,
∴四边形 是平行四边形,
∵∠ABC=90°,
∴四边形ABCD是矩形.
17(1)是直角三角形,
∵四边形是矩形,
∴,
∵将矩形纸片沿折叠,使点A落在点E处,
∴,
∴是直角三角形;
(2)∵将矩形纸片沿折叠,使点A落在点E处,
∴,
∴四边形是矩形,,
∴,
∴.
18.证明:∵是的中位线,
∴,
∴四边形为平行四边形,
∴
∴四边形为矩形,
∴.
19.(1)由翻折和长方形的性质可知,,
又∵(对顶角).
∴ .
(2)设BE=x,则EC=4-x.
由(1)得AE=EC=4-x,
在中,,即.
解得:x=.
故BE=.
20.(1)在长方形中,
,,
,
由翻折性质可知
,
又∵,
,
又∵,
∴,
,
在和中
故△ABE≌△AGF(ASA),
.
(2)令
∵AD=BC=18,
∴DF=18-x
又∵GF=DF=18-x,
AG=CD=AB=12,
∴中,
由勾股定理得,
,
故.
一、单选题
1.在四边形ABCD中,对角线AC,BD互相平分,要使四边形ABCD为矩形,需添加的条件是( )
A.∠A=∠C B.AB=BC C.AC⊥BD D.AC=BD
2.要检验一个四边形的桌面是否为矩形,可行的测量方案是( )
A.测量两条对角线是否相等
B.度量两个角是否是90°
C.测量两条对角线的交点到四个顶点的距离是否相等
D.测量两组对边是否分别相等
3.如图,在矩形中,,,点E在边上,若平分,则的长为( )
A. B. C. D.
4.如图,在矩形ABCD中,对角线AC、BD相交于点O,交BD于点E,,则的度数为( )
A.40° B.35° C.30° D.25°
5.我们把宽与长的比等于黄金比的矩形称为黄金矩形.如图,在黄金矩形中,的平分线交边于点,于点,则下列结论错误的是( )
A. B. C. D.
6.如图,在矩形中,对角线相交于点O,点E是边的中点,点F在对角线上,且,连接.若,则的长为( )
A. B.3 C.4 D.5
7.如图,在 ABCD中,O是对角线的交点,AE⊥BC于E,若△ABC的周长为12, ABCD的周长是16,则OE的值为( )
A.6 B.4 C.2 D.1
8.如图,矩形的对角线,,则的长为( )
A. B.4 C. D.8
9.如图,在中,,,点D在AB边上,,垂足分别为点E、F,连接EF,则线段EF的最小值等于多少( )
A.2.4 B.4.8 C.9.6 D.不确定
10.如图,矩形纸片中,,,按如图的方式折叠,使点与点重合,则折痕的长为( )
A. B. C. D.
二、填空题
11.四边形的对角线相交于点,且,,则_______.
12.如图,已知矩形的对角线与相交于点,若,那么______.
13.如图,平行四边形ABCD中,对角线AC,BD相交于点O,欲使四边形ABCD变成矩形,则还需添加______.(写出一个合适的条件即可)
14.如图,O是矩形ABCD的对角线的交点,M是AD的中点.若BC=8,OB=5,则OM的长为_______.
15.如图,长方形台球桌面ABCD上有两个球P,Q.PQ∥AB,球P连续撞击台球桌边AB,BC反射后,撞到球Q.已知点M,N是球在AB,BC边的撞击点,PQ=4,∠MPQ=30 ,且点P到AB边的距离为3,则四边形PMNQ的周长为__.
三、解答题
16.如图,在△ABC中,∠B=90°,O为AC的中点,连接BO并延长至D,使OD=OB,连接AD,CD,求证:四边形ABCD是矩形.
17.如图,在长方形中,,将矩形纸片沿折叠,使点A落在点E处,设与相交于点F.
(1)判断的形状,并说明理由;
(2)求的长.
18.如图,在中,是的中位线,连接.
求证:
19.如图,四边形ABCD是长方形,把△ACD沿AC折叠得到△ACD’,AD’与与BC交于点E,若AD=4,DC=3
(1)求证
(2)求BE的长
20.如图,在长方形纸片中,,将纸片折叠压平,使点与点重合,折痕为.
(1)求证:.
(2)求线段的长.
参考答案
1.D
2.C
3.C
4.B
5.C
6.A
7.C
8.C
9.B
10.C
11.1:2
12.2
13.AC=BD(答案不唯一)
14.3
15.16.
16.证明:如图,
∵O为AC的中点,
∴ ,
∵ ,
∴四边形 是平行四边形,
∵∠ABC=90°,
∴四边形ABCD是矩形.
17(1)是直角三角形,
∵四边形是矩形,
∴,
∵将矩形纸片沿折叠,使点A落在点E处,
∴,
∴是直角三角形;
(2)∵将矩形纸片沿折叠,使点A落在点E处,
∴,
∴四边形是矩形,,
∴,
∴.
18.证明:∵是的中位线,
∴,
∴四边形为平行四边形,
∴
∴四边形为矩形,
∴.
19.(1)由翻折和长方形的性质可知,,
又∵(对顶角).
∴ .
(2)设BE=x,则EC=4-x.
由(1)得AE=EC=4-x,
在中,,即.
解得:x=.
故BE=.
20.(1)在长方形中,
,,
,
由翻折性质可知
,
又∵,
,
又∵,
∴,
,
在和中
故△ABE≌△AGF(ASA),
.
(2)令
∵AD=BC=18,
∴DF=18-x
又∵GF=DF=18-x,
AG=CD=AB=12,
∴中,
由勾股定理得,
,
故.
