人教版2023年七年级下册第8章《二元一次方程组》单元检测卷 (含解析)
文档属性
| 名称 | 人教版2023年七年级下册第8章《二元一次方程组》单元检测卷 (含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 240.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-14 06:20:00 | ||
图片预览



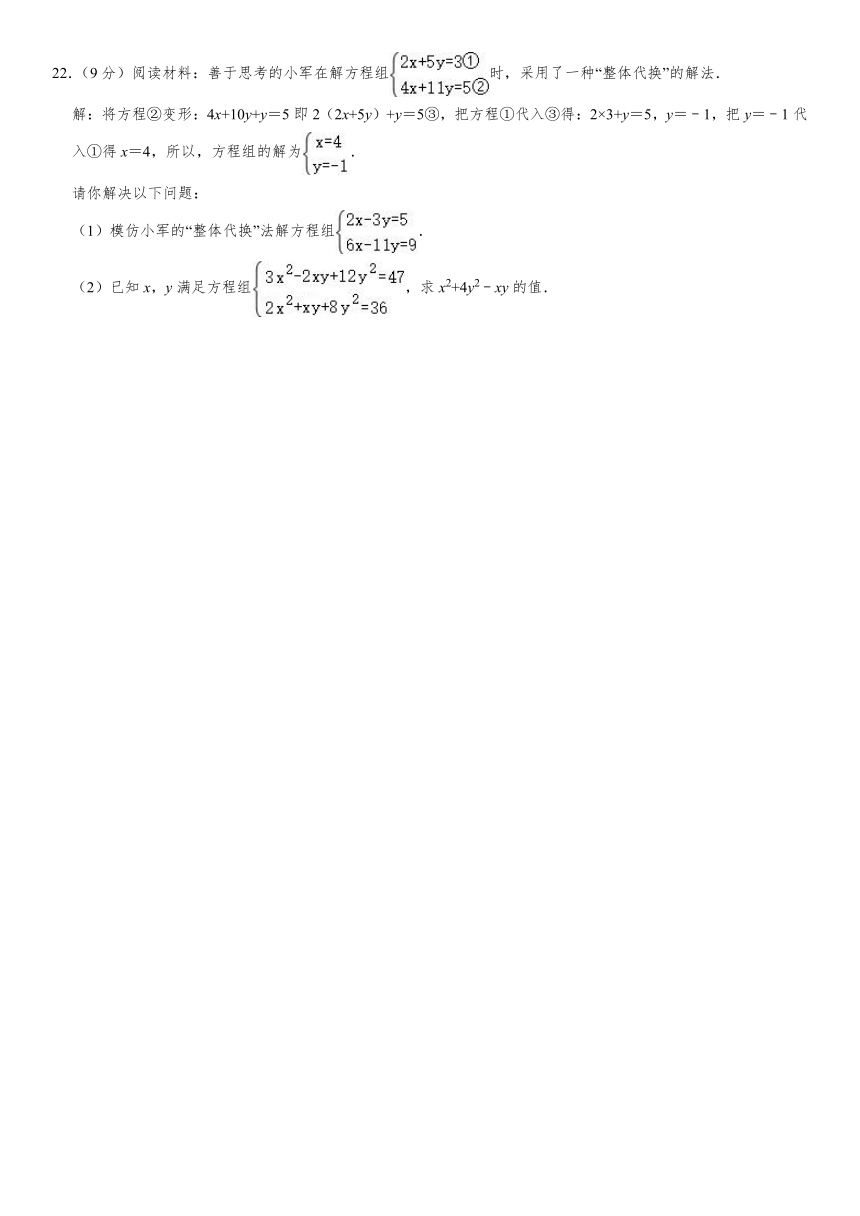

文档简介
人教版2023年七年级下册第8章《二元一次方程组》单元检测卷
一.选择题(共10小题,满分30分,每小题3分)
1.下列方程组中,是二元一次方程组的是( )
①;②;③;④
A.①② B.③④ C.①②④ D.①②③
2.已知方程组,将①代入②得( )
A.x+4x=6 B.2x+2y=6 C.x+2y=6 D.2x+y=6
3.以方程组的解为坐标的点(x,y)所在象限为( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
4.在解二元一次方程组时,若①﹣②可直接消去未知数y,则m和n满足下列条件是( )
A.m=n B.mn=1 C.m+n=0 D.m+n=1
5.关于x,y的方程4x﹣3y=7和2x+3y=﹣1的解相同,则x+3y的值为( )
A.﹣3 B.﹣2 C.﹣1 D.0
6.对于二元一次方程x+3y=10,有几组正整数解( )
A.1 B.2 C.3 D.4
7.方程组的解为,则被遮住的两个数分别为( )
A.2,1 B.5,1 C.2,3 D.2,4
8.我国民间流传一道数学名题.其题意为:一群老者去赶集,半路买了一堆梨,一人一个多一个,一人两个少两个.请问君子知道否,几个老者几个梨?没有老者x人,有梨y个,则可列二元一次方程组为( )
A. B.
C. D.
9.如图,七个相同的小长方形组成一个大长方形ABCD,若CD=21,则小长方形的面积为( )
A.80 B.90 C.610 D.630
10.已知关于x,y的方程组给出下列结论:
①当a=1时,方程组的解也是x+y=2a+1的解;
②无论a取何值,x,y的值不可能是互为相反数;
③x,y都为自然数的解有4对;
④若2x+y=8,则a=2.
正确的有几个( )
A.1 B.2 C.3 D.4
二.填空题(共6小题,满分24分,每小题4分)
11.将方程2x﹣3y=7,用含y的代数式表示x为 .
12.若关于x、y的方程xm﹣1﹣2y5+n=5是二元一次方程,则m= ,n= .
13.已知是方程3x﹣ay=5的一个解,那么a的值是 .
14.若x,y满足方程组,则x+y= .
15.把一根长15m的钢管截成2m长和3m长两种规格均有的短钢管,且没有余料,设某种截法中2m长的钢管有a根,则a的值可能有 种.
16.已知关于x,y的方程组的解是,则方程组的解是 .
三.解答题(共6小题,满分46分)
17.(6分)解下列方程组:
(1)(代入消元法);
(2)(加减消元法).
18.(6分)小李、小张两位同学同时解方程组,小李解对了,得:,小张抄错了m,得:,求原方程组中a的值.
19.(8分)某商场从厂家购进甲、乙两种文具,甲种文具的每件进价比乙种文具的每件进价少20元.若购进甲种文具7件,乙种文具2件,则需要760元.
(1)求甲、乙两种文具的每件进价分别是多少元?
(2)该商场从厂家购进甲、乙两种文具共50件,所用资金恰好为4400元.求甲、乙两种文具的件数.
20.(8分)已知,关于x,y的二元一次方程组与方程组有相同的解.
(1)求这两个方程组的相同解:
(2)求(2a+b)2023的值.
21.(9分)随着“低碳生活,绿色出行”理念的普及,新能源汽车正逐渐成为人们喜爱的交通工具.某汽车4S店计划购进一批新能源汽车进行销售.据了解,购进3辆A型新能源汽车、2辆B型新能源汽车的共需95万元;购进4辆A型新能源汽车、1辆B型新能源汽车的共需110万元.
(1)问A、B两种型号的新能源汽车每辆进价分别为多少万元?
(2)若该公司计划正好用250万元购进以上两种型号的新能源汽车(两种型号的汽车均购买),销售1辆A型汽车可获利1.2万元,销售1辆B型汽车可获利0.8万元,假如这些新能源汽车全部售出,问该公司的共有几种购买方案?最大利润是多少万元?
22.(9分)阅读材料:善于思考的小军在解方程组时,采用了一种“整体代换”的解法.
解:将方程②变形:4x+10y+y=5即2(2x+5y)+y=5③,把方程①代入③得:2×3+y=5,y=﹣1,把y=﹣1代入①得x=4,所以,方程组的解为.
请你解决以下问题:
(1)模仿小军的“整体代换”法解方程组.
(2)已知x,y满足方程组,求x2+4y2﹣xy的值.
人教版2023年七年级下册第8章《二元一次方程组》单元检测卷
参考答案
一.选择题(共10小题,满分30分,每小题3分)
1.【解答】解:①符合二元一次方程组的定义,是二元一次方程组;
②符合二元一次方程组的定义,是二元一次方程组;
③方程组含有,是分式,因此不符合二元一次方程组的定义,不是二元一次方程组;
④符合二元一次方程组的定义,是二元一次方程组;
综上,①②④是二元一次方程组.
故选:C.
2.【解答】解:将①代入②得,x+4x=6.
故选:A.
3.【解答】解:,
把①代入②得:
x+2=﹣x+3,
解得,
把代入①得:
,
则在第一象限,
故选:A.
4.【解答】解:,
由①﹣②得:4x+(m+n)y=9,
∵①﹣②可直接消去未知数y,
∴m+n=0.
故选:C.
5.【解答】解:∵关于x,y的方程4x﹣3y=7和2x+3y=﹣1的解相同,
∴可得:,
解得:,
∴x+3y=1+3×(﹣1)=﹣2,
∴x+3y的值为﹣2.
故选:B.
6.【解答】解:由题意得,0<x≤10,1≤y≤3.
当x=1,则y=3;
当x=2,则y=(不符题意,舍去);
当x=3,则y=(不符合题意,舍去);
当x=4,y=2;
当x=5,y=(不符合题意,舍去);
当x=6,y=(不符合题意,舍去);
当x=7,y=1;
当x=8,y=(不符合题意,舍去);
当x=9,y=(不符合题意,舍去);
当x=10,y=0(不符题意,故舍去).
综上:符合条件的有3组.
故选:C.
7.【解答】解:将x=2代入x+y=3得:2+y=3,
解得:y=1;
将x=2,y=1代入2x+y=□得:2×2+1=□,
解得:□=5,
∴被遮住的两个数分别为5,1.
故选:B.
8.【解答】解:依题意得.
故选:B.
9.【解答】解:设小长方形的长为x,宽为y,
根据题意得:,
解得:,
∴xy=15×6=90,
∴小长方形的面积为90.
故选:B.
10.【解答】解:①将a=1代入原方程组,得 解得
将x=3,y=0,a=1代入方程x+y=2a+1的左右两边,
左边=3,右边=3,
当a=1时,方程组的解也是x+y=2a+1的解;
②解原方程组,得
∴x+y=3,
无论a取何值,x,y的值不可能是互为相反数;
③∵x+y=2a+1+2﹣2a=3
∴x、y为自然数的解有,,,.
④∵2x+y=8,∴2(2a+1)+2﹣2a=8,
解得a=2.
故选:D.
二.填空题(共6小题,满分24分,每小题4分)
11.【解答】解:移项得﹣3y=﹣2x+7,
两边都除以﹣3得y=x﹣.
故答案为:y=x﹣.
12.【解答】解:因为关于x、y的方程xm﹣1﹣2y5+n=5是二元一次方程,
所以,
解得m=2,n=﹣4.
故答案为:2,﹣4.
13.【解答】解:把代入3x﹣ay=5得:
3×1﹣(﹣1)×a=5,
解得:a=2.
故答案为:2.
14.【解答】解:,
①﹣②,得(2x﹣3y)﹣(x﹣4y)=1﹣(﹣2),
2x﹣3y﹣x+4y=1+2,
x+y=3.
故答案为:3.
15.【解答】解:设3m长的钢管有b根,
由题意得,2a+3b=15,
∴,
∵a、b都是正整数,
∴一定是正整数,
∴2a=6或2a=12,
∴a=3或a=6,
∴a的值可能有2种,
故答案为:2.
16.【解答】解:∵方程组的可化为,
∵方程组的解是,
∴方程组中=﹣4,=3,
解得x=﹣13,y=7,
∴方程组的解是.
故答案为:.
三.解答题(共6小题,满分46分)
17.【解答】解:(1),
把①代入②得:2b+3=3b+20,
解得:b=﹣17,
把b=﹣17代入①得:a=2×(﹣17)+3,
解得:a=﹣31,
∴原方程组的解为;
(2),
由①+②得:﹣m=22,
解得:m=﹣22,
把m=﹣22代入①得:3×(﹣22)+b=11,
解得:b=77,
∴原方程组的解为.
18.【解答】解:将、代入ax+by=2,得
,
①﹣②,得
5b=0,
解得b=0,
把b=0代入①,得
﹣2a=2,
解得a=﹣1.
19.【解答】解:(1)设甲种文具每件进价为x元,则乙种文具每件进价为(x+20)元,
由题意得:7x+2(x+20)=760,
解得:x=80,
∴x+20=80+20=100,
答:甲种文具每件进价为80元,乙种文具每件进价为100元;
(2)设商场从厂家购进甲种文具a件,购进乙种文具b件,
由题意得:,
解得:,
答:商场从厂家购进甲种文具30件,乙种文具20件.
20.【解答】解:由题意得:,
①+②得:5x=10,
解得:x=2,
把x=2代入①得:4+5y=﹣26,
解得:y=﹣6,
原方程组的解为:,
∴这两个方程组的解为:;
(2)把代入中可得:,
化简得:,
①×3得:3a+9b=﹣6③,
②+③得:10b=﹣10,
解得:b=﹣1,
把b=﹣1代入②得:﹣1﹣3a=﹣4,
解得:a=1,
∴(2a+b)2023
=(2﹣1)2023
=12023
=1,
∴(2a+b)2023的值为1.
21.【解答】解:(1)设A种型号的新能源汽车每辆进价为x万元,B种型号的新能源汽车每辆进价为y万元,
根据题意得:,
解得:.
答:A种型号的新能源汽车每辆进价为25万元,B种型号的新能源汽车每辆进价为10万元;
(2)设购买m辆A种型号的新能源汽车,n辆B种型号的新能源汽车,
根据题意得:25m+10n=250,
∴m=10﹣n,
∵m,n均为正整数,
∴或或或,
∴该公司共有四种购买方案.
当m=2,n=20时,获得的利润为1.2×2+0.8×20=18.4(万元);
当m=4,n=15时,获得的利润为1.2×4+0.8×15=16.8(万元);
当m=6,n=10时,获得的利润为1.2×6+0.8×10=15.2(万元);
当m=8,n=5时,获得的利润为1.2×8+0.8×5=13.6(万元).
∵18.4>16.8>15.2>13.6,
∴最大利润是18.4万元.
22.【解答】解:(1),
由②得:3(2x﹣3y)﹣2y=9③,
把①代入③得:15﹣2y=9,
解得:y=3,
把y=3代入①得:2x﹣9=5,
解得:x=7,
所以原方程组的解为;
由①得:3(x2+4y2)﹣2xy=47,
化简得:,
把③代入②得:,
解得:xy=2,
把xy=2代入③得x2+4y2=17,
∴x2+4y2﹣xy=15.
一.选择题(共10小题,满分30分,每小题3分)
1.下列方程组中,是二元一次方程组的是( )
①;②;③;④
A.①② B.③④ C.①②④ D.①②③
2.已知方程组,将①代入②得( )
A.x+4x=6 B.2x+2y=6 C.x+2y=6 D.2x+y=6
3.以方程组的解为坐标的点(x,y)所在象限为( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
4.在解二元一次方程组时,若①﹣②可直接消去未知数y,则m和n满足下列条件是( )
A.m=n B.mn=1 C.m+n=0 D.m+n=1
5.关于x,y的方程4x﹣3y=7和2x+3y=﹣1的解相同,则x+3y的值为( )
A.﹣3 B.﹣2 C.﹣1 D.0
6.对于二元一次方程x+3y=10,有几组正整数解( )
A.1 B.2 C.3 D.4
7.方程组的解为,则被遮住的两个数分别为( )
A.2,1 B.5,1 C.2,3 D.2,4
8.我国民间流传一道数学名题.其题意为:一群老者去赶集,半路买了一堆梨,一人一个多一个,一人两个少两个.请问君子知道否,几个老者几个梨?没有老者x人,有梨y个,则可列二元一次方程组为( )
A. B.
C. D.
9.如图,七个相同的小长方形组成一个大长方形ABCD,若CD=21,则小长方形的面积为( )
A.80 B.90 C.610 D.630
10.已知关于x,y的方程组给出下列结论:
①当a=1时,方程组的解也是x+y=2a+1的解;
②无论a取何值,x,y的值不可能是互为相反数;
③x,y都为自然数的解有4对;
④若2x+y=8,则a=2.
正确的有几个( )
A.1 B.2 C.3 D.4
二.填空题(共6小题,满分24分,每小题4分)
11.将方程2x﹣3y=7,用含y的代数式表示x为 .
12.若关于x、y的方程xm﹣1﹣2y5+n=5是二元一次方程,则m= ,n= .
13.已知是方程3x﹣ay=5的一个解,那么a的值是 .
14.若x,y满足方程组,则x+y= .
15.把一根长15m的钢管截成2m长和3m长两种规格均有的短钢管,且没有余料,设某种截法中2m长的钢管有a根,则a的值可能有 种.
16.已知关于x,y的方程组的解是,则方程组的解是 .
三.解答题(共6小题,满分46分)
17.(6分)解下列方程组:
(1)(代入消元法);
(2)(加减消元法).
18.(6分)小李、小张两位同学同时解方程组,小李解对了,得:,小张抄错了m,得:,求原方程组中a的值.
19.(8分)某商场从厂家购进甲、乙两种文具,甲种文具的每件进价比乙种文具的每件进价少20元.若购进甲种文具7件,乙种文具2件,则需要760元.
(1)求甲、乙两种文具的每件进价分别是多少元?
(2)该商场从厂家购进甲、乙两种文具共50件,所用资金恰好为4400元.求甲、乙两种文具的件数.
20.(8分)已知,关于x,y的二元一次方程组与方程组有相同的解.
(1)求这两个方程组的相同解:
(2)求(2a+b)2023的值.
21.(9分)随着“低碳生活,绿色出行”理念的普及,新能源汽车正逐渐成为人们喜爱的交通工具.某汽车4S店计划购进一批新能源汽车进行销售.据了解,购进3辆A型新能源汽车、2辆B型新能源汽车的共需95万元;购进4辆A型新能源汽车、1辆B型新能源汽车的共需110万元.
(1)问A、B两种型号的新能源汽车每辆进价分别为多少万元?
(2)若该公司计划正好用250万元购进以上两种型号的新能源汽车(两种型号的汽车均购买),销售1辆A型汽车可获利1.2万元,销售1辆B型汽车可获利0.8万元,假如这些新能源汽车全部售出,问该公司的共有几种购买方案?最大利润是多少万元?
22.(9分)阅读材料:善于思考的小军在解方程组时,采用了一种“整体代换”的解法.
解:将方程②变形:4x+10y+y=5即2(2x+5y)+y=5③,把方程①代入③得:2×3+y=5,y=﹣1,把y=﹣1代入①得x=4,所以,方程组的解为.
请你解决以下问题:
(1)模仿小军的“整体代换”法解方程组.
(2)已知x,y满足方程组,求x2+4y2﹣xy的值.
人教版2023年七年级下册第8章《二元一次方程组》单元检测卷
参考答案
一.选择题(共10小题,满分30分,每小题3分)
1.【解答】解:①符合二元一次方程组的定义,是二元一次方程组;
②符合二元一次方程组的定义,是二元一次方程组;
③方程组含有,是分式,因此不符合二元一次方程组的定义,不是二元一次方程组;
④符合二元一次方程组的定义,是二元一次方程组;
综上,①②④是二元一次方程组.
故选:C.
2.【解答】解:将①代入②得,x+4x=6.
故选:A.
3.【解答】解:,
把①代入②得:
x+2=﹣x+3,
解得,
把代入①得:
,
则在第一象限,
故选:A.
4.【解答】解:,
由①﹣②得:4x+(m+n)y=9,
∵①﹣②可直接消去未知数y,
∴m+n=0.
故选:C.
5.【解答】解:∵关于x,y的方程4x﹣3y=7和2x+3y=﹣1的解相同,
∴可得:,
解得:,
∴x+3y=1+3×(﹣1)=﹣2,
∴x+3y的值为﹣2.
故选:B.
6.【解答】解:由题意得,0<x≤10,1≤y≤3.
当x=1,则y=3;
当x=2,则y=(不符题意,舍去);
当x=3,则y=(不符合题意,舍去);
当x=4,y=2;
当x=5,y=(不符合题意,舍去);
当x=6,y=(不符合题意,舍去);
当x=7,y=1;
当x=8,y=(不符合题意,舍去);
当x=9,y=(不符合题意,舍去);
当x=10,y=0(不符题意,故舍去).
综上:符合条件的有3组.
故选:C.
7.【解答】解:将x=2代入x+y=3得:2+y=3,
解得:y=1;
将x=2,y=1代入2x+y=□得:2×2+1=□,
解得:□=5,
∴被遮住的两个数分别为5,1.
故选:B.
8.【解答】解:依题意得.
故选:B.
9.【解答】解:设小长方形的长为x,宽为y,
根据题意得:,
解得:,
∴xy=15×6=90,
∴小长方形的面积为90.
故选:B.
10.【解答】解:①将a=1代入原方程组,得 解得
将x=3,y=0,a=1代入方程x+y=2a+1的左右两边,
左边=3,右边=3,
当a=1时,方程组的解也是x+y=2a+1的解;
②解原方程组,得
∴x+y=3,
无论a取何值,x,y的值不可能是互为相反数;
③∵x+y=2a+1+2﹣2a=3
∴x、y为自然数的解有,,,.
④∵2x+y=8,∴2(2a+1)+2﹣2a=8,
解得a=2.
故选:D.
二.填空题(共6小题,满分24分,每小题4分)
11.【解答】解:移项得﹣3y=﹣2x+7,
两边都除以﹣3得y=x﹣.
故答案为:y=x﹣.
12.【解答】解:因为关于x、y的方程xm﹣1﹣2y5+n=5是二元一次方程,
所以,
解得m=2,n=﹣4.
故答案为:2,﹣4.
13.【解答】解:把代入3x﹣ay=5得:
3×1﹣(﹣1)×a=5,
解得:a=2.
故答案为:2.
14.【解答】解:,
①﹣②,得(2x﹣3y)﹣(x﹣4y)=1﹣(﹣2),
2x﹣3y﹣x+4y=1+2,
x+y=3.
故答案为:3.
15.【解答】解:设3m长的钢管有b根,
由题意得,2a+3b=15,
∴,
∵a、b都是正整数,
∴一定是正整数,
∴2a=6或2a=12,
∴a=3或a=6,
∴a的值可能有2种,
故答案为:2.
16.【解答】解:∵方程组的可化为,
∵方程组的解是,
∴方程组中=﹣4,=3,
解得x=﹣13,y=7,
∴方程组的解是.
故答案为:.
三.解答题(共6小题,满分46分)
17.【解答】解:(1),
把①代入②得:2b+3=3b+20,
解得:b=﹣17,
把b=﹣17代入①得:a=2×(﹣17)+3,
解得:a=﹣31,
∴原方程组的解为;
(2),
由①+②得:﹣m=22,
解得:m=﹣22,
把m=﹣22代入①得:3×(﹣22)+b=11,
解得:b=77,
∴原方程组的解为.
18.【解答】解:将、代入ax+by=2,得
,
①﹣②,得
5b=0,
解得b=0,
把b=0代入①,得
﹣2a=2,
解得a=﹣1.
19.【解答】解:(1)设甲种文具每件进价为x元,则乙种文具每件进价为(x+20)元,
由题意得:7x+2(x+20)=760,
解得:x=80,
∴x+20=80+20=100,
答:甲种文具每件进价为80元,乙种文具每件进价为100元;
(2)设商场从厂家购进甲种文具a件,购进乙种文具b件,
由题意得:,
解得:,
答:商场从厂家购进甲种文具30件,乙种文具20件.
20.【解答】解:由题意得:,
①+②得:5x=10,
解得:x=2,
把x=2代入①得:4+5y=﹣26,
解得:y=﹣6,
原方程组的解为:,
∴这两个方程组的解为:;
(2)把代入中可得:,
化简得:,
①×3得:3a+9b=﹣6③,
②+③得:10b=﹣10,
解得:b=﹣1,
把b=﹣1代入②得:﹣1﹣3a=﹣4,
解得:a=1,
∴(2a+b)2023
=(2﹣1)2023
=12023
=1,
∴(2a+b)2023的值为1.
21.【解答】解:(1)设A种型号的新能源汽车每辆进价为x万元,B种型号的新能源汽车每辆进价为y万元,
根据题意得:,
解得:.
答:A种型号的新能源汽车每辆进价为25万元,B种型号的新能源汽车每辆进价为10万元;
(2)设购买m辆A种型号的新能源汽车,n辆B种型号的新能源汽车,
根据题意得:25m+10n=250,
∴m=10﹣n,
∵m,n均为正整数,
∴或或或,
∴该公司共有四种购买方案.
当m=2,n=20时,获得的利润为1.2×2+0.8×20=18.4(万元);
当m=4,n=15时,获得的利润为1.2×4+0.8×15=16.8(万元);
当m=6,n=10时,获得的利润为1.2×6+0.8×10=15.2(万元);
当m=8,n=5时,获得的利润为1.2×8+0.8×5=13.6(万元).
∵18.4>16.8>15.2>13.6,
∴最大利润是18.4万元.
22.【解答】解:(1),
由②得:3(2x﹣3y)﹣2y=9③,
把①代入③得:15﹣2y=9,
解得:y=3,
把y=3代入①得:2x﹣9=5,
解得:x=7,
所以原方程组的解为;
由①得:3(x2+4y2)﹣2xy=47,
化简得:,
把③代入②得:,
解得:xy=2,
把xy=2代入③得x2+4y2=17,
∴x2+4y2﹣xy=15.
