2022-2023学年北师大版九年级数学下册 第1章直角三角形的边角关系(无答案)
文档属性
| 名称 | 2022-2023学年北师大版九年级数学下册 第1章直角三角形的边角关系(无答案) | 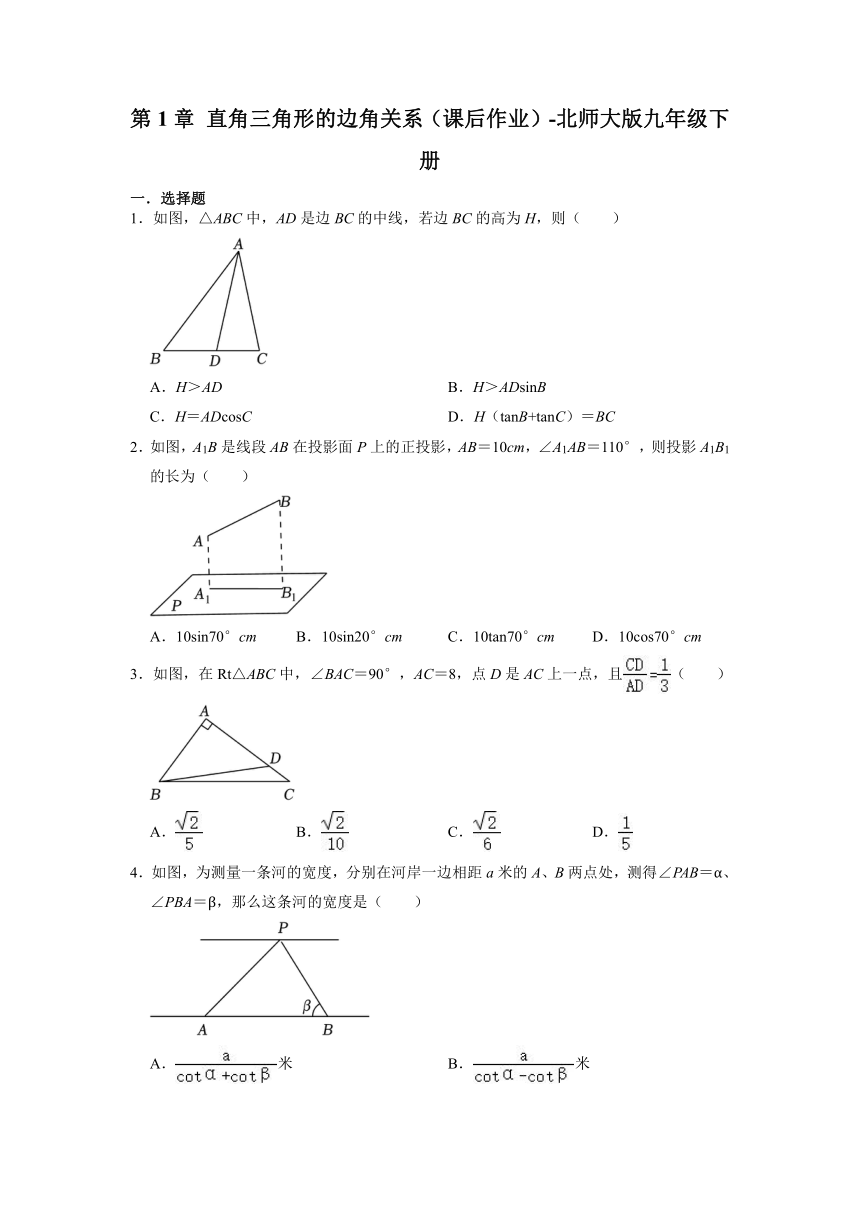 | |
| 格式 | docx | ||
| 文件大小 | 744.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-14 06:26:19 | ||
图片预览



文档简介
第1章 直角三角形的边角关系(课后作业)-北师大版九年级下册
一.选择题
1.如图,△ABC中,AD是边BC的中线,若边BC的高为H,则( )
A.H>AD B.H>ADsinB
C.H=ADcosC D.H(tanB+tanC)=BC
2.如图,A1B是线段AB在投影面P上的正投影,AB=10cm,∠A1AB=110°,则投影A1B1的长为( )
A.10sin70°cm B.10sin20°cm C.10tan70°cm D.10cos70°cm
3.如图,在Rt△ABC中,∠BAC=90°,AC=8,点D是AC上一点,且( )
A. B. C. D.
4.如图,为测量一条河的宽度,分别在河岸一边相距a米的A、B两点处,测得∠PAB=α、∠PBA=β,那么这条河的宽度是( )
A.米 B.米
C.米 D.米
5.已知函数,则f(cos30°)、f(cos45°)(cos60°)的大小关系为( )
A.f(cos30°)<f(cos45°)<f(cos60°)
B.f(cos30°)>f(cos45°)>f(cos60°)
C.f(cos45°)<f(cos30°)<f(cos60°)
D.f(cos45°)<f(cos60°)<f(cos30°)
6.如图,在Rt△ABC中,∠C=90°,,连接BD.若,,则BD的长为( )
A. B. C.3 D.
7.已知在△ABC中,∠A=60°,AB=1+,则∠C=( )
A.45° B.75° C.90° D.105°
8.如图,在△ABC中,∠ACB=90°,使BD=AB,连接CD.若,则( )
A. B.1 C. D.
9.周末,刘老师读到《行路难》中“闲来垂钓碧溪上,忽复乘舟梦日边.”邀约好友一起去江边垂钓.如图,露在水面上的鱼线BC的长为,刘老师想看看鱼钩上的情况,此时露在水面上的鱼线B′C′的长度是( )
A.3m B.2m C.2m D.3m
10.如图,某小区的一块草坪旁边有一条直角小路,社区为了方便群众进行核酸采集,已知AB=80米,新修小路与AB的夹角∠CAB为40°( )米.
A.80sin40° B.80cos40° C. D.
二.填空题
.如图,在矩形ABCD中,BD是对角线,垂足为E,连接CE,则tan∠DEC的值是 .
.如图,在Rt△ABC中,∠ACB=90°,连接CD,过点B作CD的垂线,tanA=,则cos∠DBE的值为 .
.如图,在Rt△ABC中,∠C=90°,E分别在AC,BC边上,BE=4,连接AE,交于点F,BD=10, .
.如图,一条细绳系着一个小球在平面内摆动,已知细绳从悬挂点O到球心的长度为50厘米,细绳相应所成的角为74°,那么小球在最高和最低位置时的高度差为 厘米.(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75.)
.如图,在由正三角形构成的网格图中,A、B、C三点均在格点上 .
三.解答题
.已知,图1是一辆登高云梯消防车的实物图,图2是其工作示意图(10m≤AC≤20m),且起重臂AC可绕点A在一定范围内转动,张角为∠CAE(90°≤∠CAE≤150°)
(1)当起重臂AC长度为15m,云梯消防车最高点C距离地面BD的高度为11m,求张角∠CAE的大小;
(2)已知该小区层高约为2.8m,若某9楼居民家突发险情,请问云梯能否将消防员送达该楼层进行救援?请说明理由.
.如图所示,某大楼的顶部竖有一块广告牌CD,点C、D、E在同一直线上,小明与同学们在山坡的坡脚A处测得广告牌底部D的仰角为53°,沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°,AB=10米,AE=21米.(测角器的高度忽略不计,结果精确到0.1米,参考数据:≈1.41,≈1.73,sin53°≈,cos53°≈,tan53°≈)
(1)求点B距水平地面AE的高度;
(2)若市政规定广告牌的高度不得大于7米,请问该公司的广告牌是否符合要求,并说明理由.
.图1是某型号挖掘机,该挖掘机是由基座、主臂和伸展臂构成.图2是某种工作状态下的侧面结构示意图(MN是基座的高,MP是主臂,PQ是伸展臂,EM∥QN).已知基座高度MN为1m,测得主臂伸展角.∠PME=37°.
(参考数据:sin37°≈,tan37°≈,sin53°≈,tan53°≈)
(1)求点P到地面的高度;
(2)若挖掘机能挖的最远处点Q到点N的距离为7m,求∠QPM的度数.
.“五一”节期间,洞庭湖旅游度假区特色文旅活动精彩上演,吸引众多市民打卡游玩,为遮阳和防雨游客们搭建了一种“天幕”,其截面示意图是轴对称图形,用绳子拉直AD后系在树干EF上的点E处,使得A,D,通过调节点E的高度可控制“天幕”的开合,AC=AD=2m
(1)天晴时打开“天幕”,若∠α=70°,求遮阳宽度CD(结果精确到0.1m);
(2)下雨时收拢“天幕”,∠α从70°减少到45°,求点E下降的高度(结果精确到0.1m).
(参考数据:sin70°≈0.94,cos70°≈0.34,tan70°≈2.75,)
.交通安全心系千万家,高速公路管理局在某隧道内安装了测速仪,如图所示的是该段隧道的截面示意图.测速仪C和测速仪E到路面之间的距离CD=EF,一辆小汽车在水平的公路上由西向东匀速行驶,在测速仪C处测得小汽车在隧道入口A点的俯角为25°,在测速仪E处测得小汽车在B点的俯角为60°,小汽车在隧道中从点A行驶到点B所用的时间为38s(图中所有点都在同一平面内).
(1)求A,B两点之间的距离(结果精确到1m);
(2)若该隧道限速22m/s,判断小汽车从点A行驶到点B是否超速?通过计算说明理由.
(参考数据:1.7,sin25°≈0.4,cos25°≈0.9,tan25°≈0.5,sin65°≈0.9,cos65°≈0.4,tan65°≈2.1)
一.选择题
1.如图,△ABC中,AD是边BC的中线,若边BC的高为H,则( )
A.H>AD B.H>ADsinB
C.H=ADcosC D.H(tanB+tanC)=BC
2.如图,A1B是线段AB在投影面P上的正投影,AB=10cm,∠A1AB=110°,则投影A1B1的长为( )
A.10sin70°cm B.10sin20°cm C.10tan70°cm D.10cos70°cm
3.如图,在Rt△ABC中,∠BAC=90°,AC=8,点D是AC上一点,且( )
A. B. C. D.
4.如图,为测量一条河的宽度,分别在河岸一边相距a米的A、B两点处,测得∠PAB=α、∠PBA=β,那么这条河的宽度是( )
A.米 B.米
C.米 D.米
5.已知函数,则f(cos30°)、f(cos45°)(cos60°)的大小关系为( )
A.f(cos30°)<f(cos45°)<f(cos60°)
B.f(cos30°)>f(cos45°)>f(cos60°)
C.f(cos45°)<f(cos30°)<f(cos60°)
D.f(cos45°)<f(cos60°)<f(cos30°)
6.如图,在Rt△ABC中,∠C=90°,,连接BD.若,,则BD的长为( )
A. B. C.3 D.
7.已知在△ABC中,∠A=60°,AB=1+,则∠C=( )
A.45° B.75° C.90° D.105°
8.如图,在△ABC中,∠ACB=90°,使BD=AB,连接CD.若,则( )
A. B.1 C. D.
9.周末,刘老师读到《行路难》中“闲来垂钓碧溪上,忽复乘舟梦日边.”邀约好友一起去江边垂钓.如图,露在水面上的鱼线BC的长为,刘老师想看看鱼钩上的情况,此时露在水面上的鱼线B′C′的长度是( )
A.3m B.2m C.2m D.3m
10.如图,某小区的一块草坪旁边有一条直角小路,社区为了方便群众进行核酸采集,已知AB=80米,新修小路与AB的夹角∠CAB为40°( )米.
A.80sin40° B.80cos40° C. D.
二.填空题
.如图,在矩形ABCD中,BD是对角线,垂足为E,连接CE,则tan∠DEC的值是 .
.如图,在Rt△ABC中,∠ACB=90°,连接CD,过点B作CD的垂线,tanA=,则cos∠DBE的值为 .
.如图,在Rt△ABC中,∠C=90°,E分别在AC,BC边上,BE=4,连接AE,交于点F,BD=10, .
.如图,一条细绳系着一个小球在平面内摆动,已知细绳从悬挂点O到球心的长度为50厘米,细绳相应所成的角为74°,那么小球在最高和最低位置时的高度差为 厘米.(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75.)
.如图,在由正三角形构成的网格图中,A、B、C三点均在格点上 .
三.解答题
.已知,图1是一辆登高云梯消防车的实物图,图2是其工作示意图(10m≤AC≤20m),且起重臂AC可绕点A在一定范围内转动,张角为∠CAE(90°≤∠CAE≤150°)
(1)当起重臂AC长度为15m,云梯消防车最高点C距离地面BD的高度为11m,求张角∠CAE的大小;
(2)已知该小区层高约为2.8m,若某9楼居民家突发险情,请问云梯能否将消防员送达该楼层进行救援?请说明理由.
.如图所示,某大楼的顶部竖有一块广告牌CD,点C、D、E在同一直线上,小明与同学们在山坡的坡脚A处测得广告牌底部D的仰角为53°,沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°,AB=10米,AE=21米.(测角器的高度忽略不计,结果精确到0.1米,参考数据:≈1.41,≈1.73,sin53°≈,cos53°≈,tan53°≈)
(1)求点B距水平地面AE的高度;
(2)若市政规定广告牌的高度不得大于7米,请问该公司的广告牌是否符合要求,并说明理由.
.图1是某型号挖掘机,该挖掘机是由基座、主臂和伸展臂构成.图2是某种工作状态下的侧面结构示意图(MN是基座的高,MP是主臂,PQ是伸展臂,EM∥QN).已知基座高度MN为1m,测得主臂伸展角.∠PME=37°.
(参考数据:sin37°≈,tan37°≈,sin53°≈,tan53°≈)
(1)求点P到地面的高度;
(2)若挖掘机能挖的最远处点Q到点N的距离为7m,求∠QPM的度数.
.“五一”节期间,洞庭湖旅游度假区特色文旅活动精彩上演,吸引众多市民打卡游玩,为遮阳和防雨游客们搭建了一种“天幕”,其截面示意图是轴对称图形,用绳子拉直AD后系在树干EF上的点E处,使得A,D,通过调节点E的高度可控制“天幕”的开合,AC=AD=2m
(1)天晴时打开“天幕”,若∠α=70°,求遮阳宽度CD(结果精确到0.1m);
(2)下雨时收拢“天幕”,∠α从70°减少到45°,求点E下降的高度(结果精确到0.1m).
(参考数据:sin70°≈0.94,cos70°≈0.34,tan70°≈2.75,)
.交通安全心系千万家,高速公路管理局在某隧道内安装了测速仪,如图所示的是该段隧道的截面示意图.测速仪C和测速仪E到路面之间的距离CD=EF,一辆小汽车在水平的公路上由西向东匀速行驶,在测速仪C处测得小汽车在隧道入口A点的俯角为25°,在测速仪E处测得小汽车在B点的俯角为60°,小汽车在隧道中从点A行驶到点B所用的时间为38s(图中所有点都在同一平面内).
(1)求A,B两点之间的距离(结果精确到1m);
(2)若该隧道限速22m/s,判断小汽车从点A行驶到点B是否超速?通过计算说明理由.
(参考数据:1.7,sin25°≈0.4,cos25°≈0.9,tan25°≈0.5,sin65°≈0.9,cos65°≈0.4,tan65°≈2.1)
