17.3 分式应用题[下学期]
图片预览






文档简介
课件14张PPT。列分式方程解应用题教材分析教学过程列分式方程解应用题教学目的:
1、使学生能分析题目中的等量关系,掌握列分式方程解应用题和解决问题的能力;
2、通过列分式方程解应用题,渗透方程的思想方法。
教学重点:列分式方程解应用题
教学难点:根据题意,找出相等关系,正确列出方程
1、解分式方程
一个“必须”是:必须 ;
二个“基本”是:
基本思想是 ,
基本方法是 ;
三个“步骤”
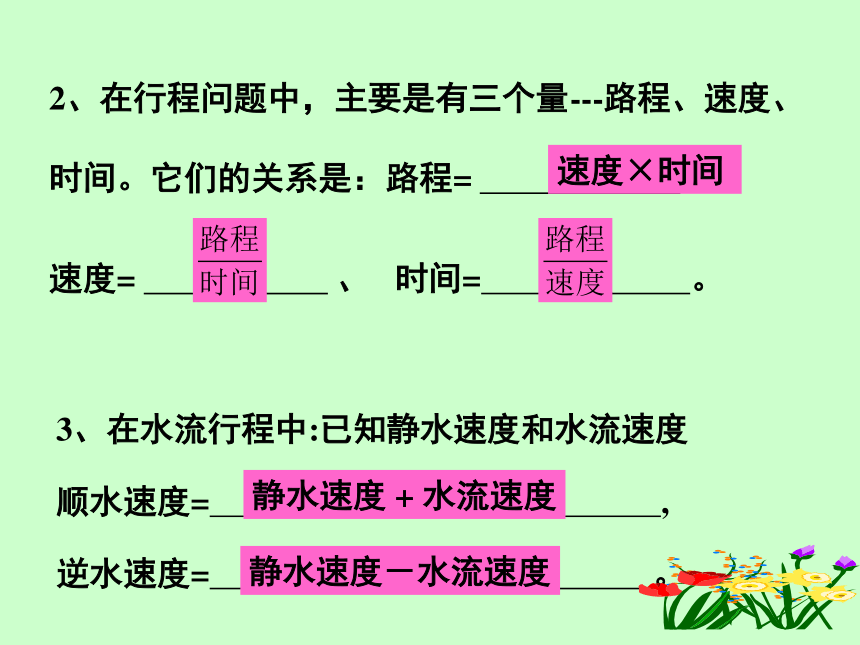
是: , , 。转化去分母去分母解整式方程检验检验填空复习2、在行程问题中,主要是有三个量---路程、速度、时间。它们的关系是:路程= 、
速度= 、 时间= 。 3、在水流行程中:已知静水速度和水流速度
顺水速度= ,
逆水速度= 。速度×时间静水速度 + 水流速度静水速度-水流速度列方程解应用题的步骤:(1)审题。(3)设未知数,列方程。(2)弄清各个量之间的关系。找出等量关系。(4)解方程。(5)答题。例举 工 效 问 题 一项工程 , 甲单独做 a h 完成, 乙单独做 b h 完成 .
甲、乙两人一起完成这项工程,需要多长时间?设 “甲、乙两人一起完成这项工程” 需要 x h , 例 :根据规划设计,某市工程队准备在开发区修建一条长1120m的盲道. 由于采用新的施工方式 , 实际每天修建盲道的长度比原计划增加10m, 从而缩短了工期.
假设原计划每天修建盲道 x m , 那么
(1) 原计划修建这条盲道需要多少天?
(2) 实际修建这条盲道的工期比原计划缩短了几天?原计划修建这条盲道需要 天;∵ 实际每天修建盲道的长度 = m ,∴ 实际修建这条盲道用了 天 .因此 , 实际修建这条盲道的工期比原计划缩短了(x+10)解例1 农机厂到距15千米的某地检修农机。一部分人骑自行车先走,过了40分,其余的人乘汽车出发。结果他们同时到达。若汽车的速度是自行车的3倍,求两种车的速度。解:设自行车的速度是x千米/时,汽车的速度为3 x千米/时。依题意得:1515x3x例2 一台甲型拖拉机4天耕完一块耕地的一半,加一台乙型拖拉机合耕,1天耕完这块地的另一半。乙型拖拉机单独耕这块地需要几天?分析:一块耕地是工作总量,可设为 .
1、若设乙型拖拉机单独耕块这地需要x天完成,那么它1天耕地量是这块地 .
2、一台甲型拖拉机4天耕完这块地的一半。那么1天耕地量是这块地的 .
3、两台拖拉机合耕这块地,1天耕地量是这块地的 . 14、列方程的依据是: 。甲、乙合作1天完成这块地的一半例3 一船在静水中每小时航行20千米,顺水航行72千米的时间恰好等于逆水航行48千米的时间,求水流速度。解:设水流每小时流动x千米。7248 提高题 用大小两种箱子包装720件产品,有三种包装方案:
方案一:产品的一半用大箱装,一半用小箱装,要用75只箱子;
方案二:产品的 用大箱装,其余用小箱装;
方案三:产品的 用大箱装,其余用小箱装,则比“方案一”可少用5只箱子;
如果每只大箱子的包装费比每只小箱子的包装费高k%,试确定选择哪种包装方案能使包装费用最低。
练习1 一项工程在规定的时间内完成,如果甲独做正好如期完成,如果乙独做要超过规定时间6天才能完成。现在,甲、乙二人合作4天后,余下的工程由乙单独做,正好如期完成,原计划规定的日期是几天? 分析设原计划规定的日期为x天
(1)甲、乙两人每天完成全部工程的 ;(2)甲、乙二人合作4天做 ;余下的工程由乙单独做 天,又做了 ;
(3)一般全工程我们设为1,那么它还有什么表示方法?
。
练习2 甲、乙两人骑自行车各行28公里,甲比乙快
小时,已知甲与乙速度比为8:7,求两人速度。解:设甲的速度8x千米/时,
乙的速度是7x千米/时。小结 1. 列分式方程解应用题与一元一次方程解应用题的方法与步骤基本相同,
2.不同点是,解分式方程必须要验根。一方面要看原方程是否有增根,另一方面还要看解出的根是否符合题意,原方程的增根和不符合题意的根都应舍去。
1、使学生能分析题目中的等量关系,掌握列分式方程解应用题和解决问题的能力;
2、通过列分式方程解应用题,渗透方程的思想方法。
教学重点:列分式方程解应用题
教学难点:根据题意,找出相等关系,正确列出方程
1、解分式方程
一个“必须”是:必须 ;
二个“基本”是:
基本思想是 ,
基本方法是 ;
三个“步骤”
是: , , 。转化去分母去分母解整式方程检验检验填空复习2、在行程问题中,主要是有三个量---路程、速度、时间。它们的关系是:路程= 、
速度= 、 时间= 。 3、在水流行程中:已知静水速度和水流速度
顺水速度= ,
逆水速度= 。速度×时间静水速度 + 水流速度静水速度-水流速度列方程解应用题的步骤:(1)审题。(3)设未知数,列方程。(2)弄清各个量之间的关系。找出等量关系。(4)解方程。(5)答题。例举 工 效 问 题 一项工程 , 甲单独做 a h 完成, 乙单独做 b h 完成 .
甲、乙两人一起完成这项工程,需要多长时间?设 “甲、乙两人一起完成这项工程” 需要 x h , 例 :根据规划设计,某市工程队准备在开发区修建一条长1120m的盲道. 由于采用新的施工方式 , 实际每天修建盲道的长度比原计划增加10m, 从而缩短了工期.
假设原计划每天修建盲道 x m , 那么
(1) 原计划修建这条盲道需要多少天?
(2) 实际修建这条盲道的工期比原计划缩短了几天?原计划修建这条盲道需要 天;∵ 实际每天修建盲道的长度 = m ,∴ 实际修建这条盲道用了 天 .因此 , 实际修建这条盲道的工期比原计划缩短了(x+10)解例1 农机厂到距15千米的某地检修农机。一部分人骑自行车先走,过了40分,其余的人乘汽车出发。结果他们同时到达。若汽车的速度是自行车的3倍,求两种车的速度。解:设自行车的速度是x千米/时,汽车的速度为3 x千米/时。依题意得:1515x3x例2 一台甲型拖拉机4天耕完一块耕地的一半,加一台乙型拖拉机合耕,1天耕完这块地的另一半。乙型拖拉机单独耕这块地需要几天?分析:一块耕地是工作总量,可设为 .
1、若设乙型拖拉机单独耕块这地需要x天完成,那么它1天耕地量是这块地 .
2、一台甲型拖拉机4天耕完这块地的一半。那么1天耕地量是这块地的 .
3、两台拖拉机合耕这块地,1天耕地量是这块地的 . 14、列方程的依据是: 。甲、乙合作1天完成这块地的一半例3 一船在静水中每小时航行20千米,顺水航行72千米的时间恰好等于逆水航行48千米的时间,求水流速度。解:设水流每小时流动x千米。7248 提高题 用大小两种箱子包装720件产品,有三种包装方案:
方案一:产品的一半用大箱装,一半用小箱装,要用75只箱子;
方案二:产品的 用大箱装,其余用小箱装;
方案三:产品的 用大箱装,其余用小箱装,则比“方案一”可少用5只箱子;
如果每只大箱子的包装费比每只小箱子的包装费高k%,试确定选择哪种包装方案能使包装费用最低。
练习1 一项工程在规定的时间内完成,如果甲独做正好如期完成,如果乙独做要超过规定时间6天才能完成。现在,甲、乙二人合作4天后,余下的工程由乙单独做,正好如期完成,原计划规定的日期是几天? 分析设原计划规定的日期为x天
(1)甲、乙两人每天完成全部工程的 ;(2)甲、乙二人合作4天做 ;余下的工程由乙单独做 天,又做了 ;
(3)一般全工程我们设为1,那么它还有什么表示方法?
。
练习2 甲、乙两人骑自行车各行28公里,甲比乙快
小时,已知甲与乙速度比为8:7,求两人速度。解:设甲的速度8x千米/时,
乙的速度是7x千米/时。小结 1. 列分式方程解应用题与一元一次方程解应用题的方法与步骤基本相同,
2.不同点是,解分式方程必须要验根。一方面要看原方程是否有增根,另一方面还要看解出的根是否符合题意,原方程的增根和不符合题意的根都应舍去。
