人教版八年级下册18.2.3 正方形 同步练习(含答案)
文档属性
| 名称 | 人教版八年级下册18.2.3 正方形 同步练习(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 357.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-14 07:23:25 | ||
图片预览


文档简介
18.2.3 正方形 同步练习
班级:_________ 姓名:_________ 学号:__________
选择题(本大题共10小题,在每小题列出的选项中,选出符合题目的一项)
1.下列命题正确的是( )
A.对角线互相垂直平分的四边形是正方形 B.对角线相等的平行四边形是正方形
C.对角线互相平分的矩形是正方形 D.对角线相等的菱形是正方形
2.如图,在中,,,,以AB为一条边向三角形外部作正方形,则正方形的面积是( )
A.13 B.12 C.6 D.3
3.如图,正方形ABCD的边长为3cm,∠ABE=,且AB=AE,则DE的长度为( )
A.3 B.4 C.5 D.6
4.七巧板是我国古代的一种拼板玩具,它已经有两千五百多年的历史了.如图所示的七巧板中,若平行四边形BEFG的周长等于10,则△BCD的周长等于( )
A.10 B.15 C.20 D.25
5.如图,在正方形中,平分交于点,点是边上一点,连接,若,则的度数为( )
A. B. C. D.
6.一个四边形顺次添加下列中的三个条件便得到正方形:
a.两组对边分别相等 b.一组对边平行且相等
c.一组邻边相等 d.一个角是直角
顺次添加的条件:①a→c→d②b→d→c③a→b→c
则正确的是:( )
A.仅① B.仅③ C.①② D.②③
7.如图,将正方形OABC放在平面直角坐标系中,O是原点,点A的坐标为(1,),则点C的坐标为( )
A.(﹣1,﹣) B.(,﹣1) C.(﹣1,) D.(﹣,1)
8.如图,点P是线段AB上任意一点,在AB同侧作正方形ACDP、正方形PEFB,连接DF、PF,已知AB=10,当△PDF的面积为8时,AP的长为( )
A.2 B.8 C.2或8 D.4
9.如图,正方形ABCD边长为1,以AC为边作第2个正方形ACEF,再以CF为边作第3个正方形FCGH,…,按照这样的规律作下去,第6个正方形的边长为( )
A.(2)5 B.(2)6 C.()5 D.()6
10.如图,正方形的边长为8,点M在上,且,N是上一动点,则的最小值为( ).
A.8 B. C. D.10
二、填空题(本大题共5小题,在横线上填上合理的答案)
11.如图,在矩形中,有以下结论:①是等腰三角形;②;③;④;⑤当时,矩形会变成正方形.正确的结论是_____.
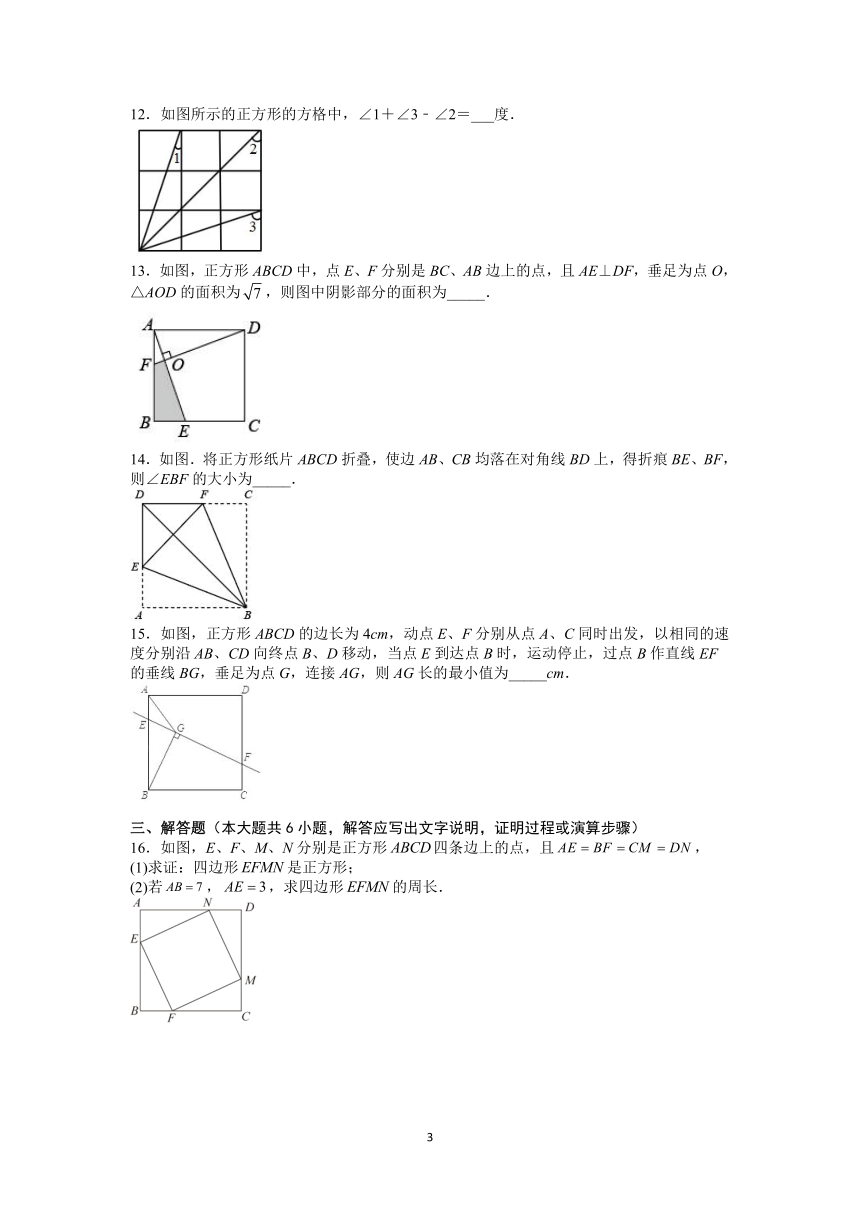
12.如图所示的正方形的方格中,∠1+∠3﹣∠2=___度.
13.如图,正方形ABCD中,点E、F分别是BC、AB边上的点,且AE⊥DF,垂足为点O,△AOD的面积为,则图中阴影部分的面积为_____.
14.如图.将正方形纸片ABCD折叠,使边AB、CB均落在对角线BD上,得折痕BE、BF,则∠EBF的大小为_____.
15.如图,正方形ABCD的边长为4cm,动点E、F分别从点A、C同时出发,以相同的速度分别沿AB、CD向终点B、D移动,当点E到达点B时,运动停止,过点B作直线EF的垂线BG,垂足为点G,连接AG,则AG长的最小值为_____cm.
三、解答题(本大题共6小题,解答应写出文字说明,证明过程或演算步骤)
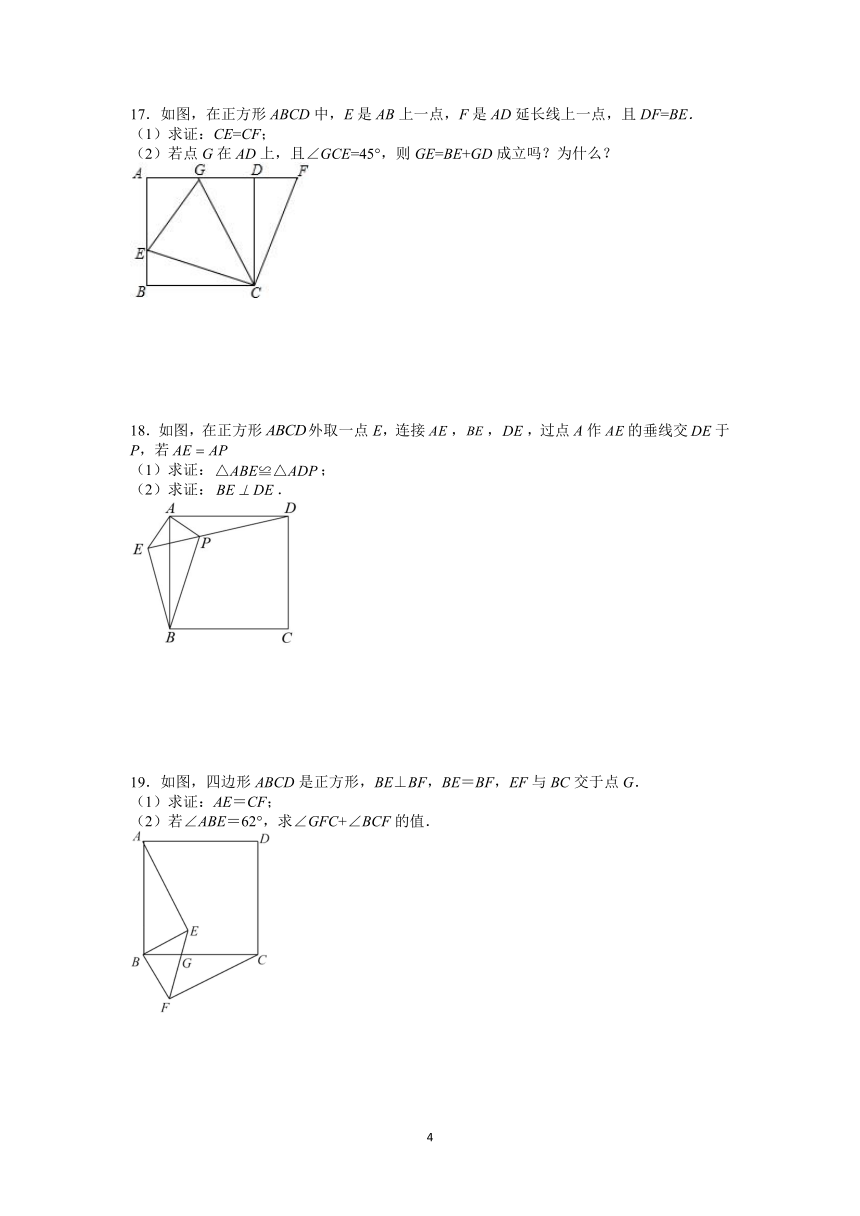
16.如图,E、F、M、N分别是正方形四条边上的点,且,
(1)求证:四边形是正方形;
(2)若,,求四边形的周长.
17.如图,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE.
(1)求证:CE=CF;
(2)若点G在AD上,且∠GCE=45°,则GE=BE+GD成立吗?为什么?
18.如图,在正方形外取一点E,连接,,,过点A作的垂线交于P,若
(1)求证:;
(2)求证:.
19.如图,四边形ABCD是正方形,BE⊥BF,BE=BF,EF与BC交于点G.
(1)求证:AE=CF;
(2)若∠ABE=62°,求∠GFC+∠BCF的值.
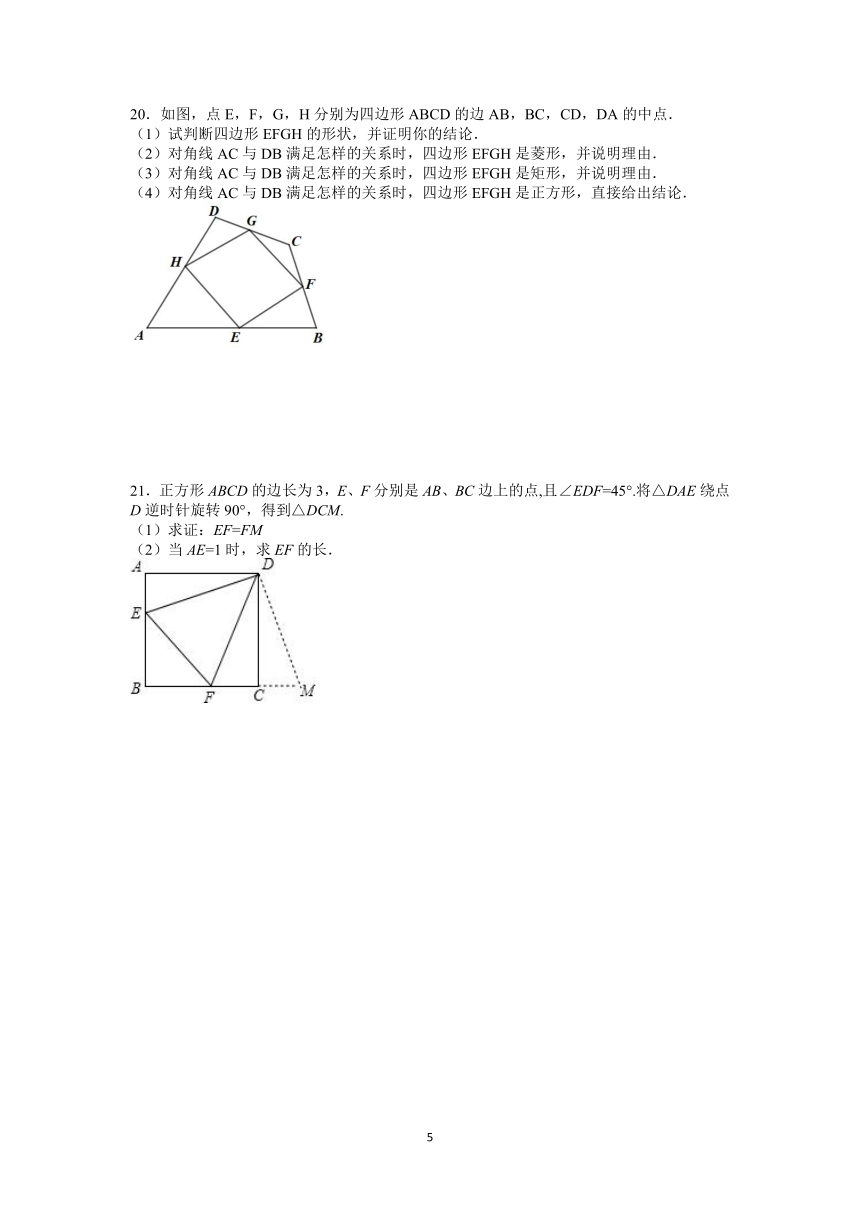
20.如图,点E,F,G,H分别为四边形ABCD的边AB,BC,CD,DA的中点.
(1)试判断四边形EFGH的形状,并证明你的结论.
(2)对角线AC与DB满足怎样的关系时,四边形EFGH是菱形,并说明理由.
(3)对角线AC与DB满足怎样的关系时,四边形EFGH是矩形,并说明理由.
(4)对角线AC与DB满足怎样的关系时,四边形EFGH是正方形,直接给出结论.
21.正方形ABCD的边长为3,E、F分别是AB、BC边上的点,且∠EDF=45°.将△DAE绕点D逆时针旋转90°,得到△DCM.
(1)求证:EF=FM
(2)当AE=1时,求EF的长.
答案:
1.D 2.A 3.A 4.C 5.C 6.C 7.D 8.C 9.C 10.D
11.①②③⑤ 12.45 13. 14.45° 15..
16(1)证明:∵,
∴,
∵,
∴,
∴,,
∴四边形是菱形,
∵,
∴,
∴,
∴四边形是正方形;
(2)解:∵,,
∴,
∴,
∴正方形EFMN的周长为:.
17.解:(1)在正方形ABCD中,BC=CD,∠B=∠CDF=90°,
∵,
∴△CBE△CDF(SAS).
∴CE=CF.
(2)GE=BE+GD成立.
理由:∵由(1)得:△CBE△CDF,
∴∠BCE=∠DCF,
∴∠BCE+∠ECD=∠DCF+∠ECD,即∠ECF=∠BCD=90°,
又∵∠GCE=45°,
∴∠GCF=∠GCE=45°,CE=CF.
∵∠GCE=∠GCF, GC=GC,
∴△ECG△FCG(SAS).
∴GE=GF.
∴GE=DF+GD=BE+GD.
18.(1)证明:∵四边形ABCD是正方形,
∴AB=AD,∠BAD=90°,
∵AE⊥AP,
∴∠EAP=90°,
∴∠EAB=∠PAD,
在△ABE和△ADP中,,
∴△ABE≌△ADP;
(2)证明:∵△ABE≌△ADP,
∴∠APD=∠AEB,
又∵∠AEB=∠AEP+∠BEP,∠APD=∠AEP+∠PAE,
∴∠BEP=∠PAE=90°,
∴BE⊥DE.
19.(1)证明:∵四边形ABCD是正方形,
∴,,
∵,
∴,
∵°,,
∴,
在和中,
,
∴,
∴;
(2)解:∵BE⊥BF,
∴,
又∵,
∴,
∵四边形ABCD是正方形,
∴,
∵,
∴,
∴.
∴的值为.
20.(1)连接AC、BD,
∵ E,F分别是AB、BC的中点,
∴EF// AC, EF=AC,
同理HG∥AC,GH =AC,
∴EF// HG, EF= HG,
∴四边形EFGH是平行四边形;
(2)当AC = BD时,四边形EFGH是菱形,
∵G、H是CD和AD的中点,
∴GH=AC,GH//AC
∵EH=BD,
∴GH = EH,
又∵四边形EFGH是平行四边形,
∴四边形EFGH是菱形;
(3)AC⊥BD,平行四边形EFGH就是矩形.
∵E、F、G、H分别是AB、BC、CD、DA的中点,
∴EH//BD, FG// BD,EF//AC,HG// AC;
当AC⊥BD时,
∵EH∥BD,FG∥BD,EF∥AC,HG// AC;
∴.EH⊥EF,EF⊥GF,HG⊥FG,HG⊥EH,
∴∠GHE=∠HEF=∠EFG=90°
∴EFGH就是矩形.
(4)当AC= BD且AC⊥BD时,四边形EFGH是正方形,
∵AC⊥BD,GH//AC,
∴GH⊥BD,
∵EH//BD,
∴GH⊥EH,
又∵四边形EFGH是菱形,
∴四边形EFGH是正方形;
故答案为: AC= BD且AC⊥BD.
21.(1)∵△DAE逆时针旋转90°得到△DCM,
∴DE=DM ,∠EDM=90°,
∴∠EDF + ∠FDM=90°,
∵∠EDF=45°,
∴∠FDM =∠EDM=45°,
∵ DF= DF,
∴△DEF≌△DMF,
∴ EF=MF
(2) 设EF=x,
∵AE=CM=1 ,
∴ BF=BM-MF=BM-EF=4-x,
∵ EB=2,
在Rt△EBF中,由勾股定理得,
即,
解得,.
班级:_________ 姓名:_________ 学号:__________
选择题(本大题共10小题,在每小题列出的选项中,选出符合题目的一项)
1.下列命题正确的是( )
A.对角线互相垂直平分的四边形是正方形 B.对角线相等的平行四边形是正方形
C.对角线互相平分的矩形是正方形 D.对角线相等的菱形是正方形
2.如图,在中,,,,以AB为一条边向三角形外部作正方形,则正方形的面积是( )
A.13 B.12 C.6 D.3
3.如图,正方形ABCD的边长为3cm,∠ABE=,且AB=AE,则DE的长度为( )
A.3 B.4 C.5 D.6
4.七巧板是我国古代的一种拼板玩具,它已经有两千五百多年的历史了.如图所示的七巧板中,若平行四边形BEFG的周长等于10,则△BCD的周长等于( )
A.10 B.15 C.20 D.25
5.如图,在正方形中,平分交于点,点是边上一点,连接,若,则的度数为( )
A. B. C. D.
6.一个四边形顺次添加下列中的三个条件便得到正方形:
a.两组对边分别相等 b.一组对边平行且相等
c.一组邻边相等 d.一个角是直角
顺次添加的条件:①a→c→d②b→d→c③a→b→c
则正确的是:( )
A.仅① B.仅③ C.①② D.②③
7.如图,将正方形OABC放在平面直角坐标系中,O是原点,点A的坐标为(1,),则点C的坐标为( )
A.(﹣1,﹣) B.(,﹣1) C.(﹣1,) D.(﹣,1)
8.如图,点P是线段AB上任意一点,在AB同侧作正方形ACDP、正方形PEFB,连接DF、PF,已知AB=10,当△PDF的面积为8时,AP的长为( )
A.2 B.8 C.2或8 D.4
9.如图,正方形ABCD边长为1,以AC为边作第2个正方形ACEF,再以CF为边作第3个正方形FCGH,…,按照这样的规律作下去,第6个正方形的边长为( )
A.(2)5 B.(2)6 C.()5 D.()6
10.如图,正方形的边长为8,点M在上,且,N是上一动点,则的最小值为( ).
A.8 B. C. D.10
二、填空题(本大题共5小题,在横线上填上合理的答案)
11.如图,在矩形中,有以下结论:①是等腰三角形;②;③;④;⑤当时,矩形会变成正方形.正确的结论是_____.
12.如图所示的正方形的方格中,∠1+∠3﹣∠2=___度.
13.如图,正方形ABCD中,点E、F分别是BC、AB边上的点,且AE⊥DF,垂足为点O,△AOD的面积为,则图中阴影部分的面积为_____.
14.如图.将正方形纸片ABCD折叠,使边AB、CB均落在对角线BD上,得折痕BE、BF,则∠EBF的大小为_____.
15.如图,正方形ABCD的边长为4cm,动点E、F分别从点A、C同时出发,以相同的速度分别沿AB、CD向终点B、D移动,当点E到达点B时,运动停止,过点B作直线EF的垂线BG,垂足为点G,连接AG,则AG长的最小值为_____cm.
三、解答题(本大题共6小题,解答应写出文字说明,证明过程或演算步骤)
16.如图,E、F、M、N分别是正方形四条边上的点,且,
(1)求证:四边形是正方形;
(2)若,,求四边形的周长.
17.如图,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE.
(1)求证:CE=CF;
(2)若点G在AD上,且∠GCE=45°,则GE=BE+GD成立吗?为什么?
18.如图,在正方形外取一点E,连接,,,过点A作的垂线交于P,若
(1)求证:;
(2)求证:.
19.如图,四边形ABCD是正方形,BE⊥BF,BE=BF,EF与BC交于点G.
(1)求证:AE=CF;
(2)若∠ABE=62°,求∠GFC+∠BCF的值.
20.如图,点E,F,G,H分别为四边形ABCD的边AB,BC,CD,DA的中点.
(1)试判断四边形EFGH的形状,并证明你的结论.
(2)对角线AC与DB满足怎样的关系时,四边形EFGH是菱形,并说明理由.
(3)对角线AC与DB满足怎样的关系时,四边形EFGH是矩形,并说明理由.
(4)对角线AC与DB满足怎样的关系时,四边形EFGH是正方形,直接给出结论.
21.正方形ABCD的边长为3,E、F分别是AB、BC边上的点,且∠EDF=45°.将△DAE绕点D逆时针旋转90°,得到△DCM.
(1)求证:EF=FM
(2)当AE=1时,求EF的长.
答案:
1.D 2.A 3.A 4.C 5.C 6.C 7.D 8.C 9.C 10.D
11.①②③⑤ 12.45 13. 14.45° 15..
16(1)证明:∵,
∴,
∵,
∴,
∴,,
∴四边形是菱形,
∵,
∴,
∴,
∴四边形是正方形;
(2)解:∵,,
∴,
∴,
∴正方形EFMN的周长为:.
17.解:(1)在正方形ABCD中,BC=CD,∠B=∠CDF=90°,
∵,
∴△CBE△CDF(SAS).
∴CE=CF.
(2)GE=BE+GD成立.
理由:∵由(1)得:△CBE△CDF,
∴∠BCE=∠DCF,
∴∠BCE+∠ECD=∠DCF+∠ECD,即∠ECF=∠BCD=90°,
又∵∠GCE=45°,
∴∠GCF=∠GCE=45°,CE=CF.
∵∠GCE=∠GCF, GC=GC,
∴△ECG△FCG(SAS).
∴GE=GF.
∴GE=DF+GD=BE+GD.
18.(1)证明:∵四边形ABCD是正方形,
∴AB=AD,∠BAD=90°,
∵AE⊥AP,
∴∠EAP=90°,
∴∠EAB=∠PAD,
在△ABE和△ADP中,,
∴△ABE≌△ADP;
(2)证明:∵△ABE≌△ADP,
∴∠APD=∠AEB,
又∵∠AEB=∠AEP+∠BEP,∠APD=∠AEP+∠PAE,
∴∠BEP=∠PAE=90°,
∴BE⊥DE.
19.(1)证明:∵四边形ABCD是正方形,
∴,,
∵,
∴,
∵°,,
∴,
在和中,
,
∴,
∴;
(2)解:∵BE⊥BF,
∴,
又∵,
∴,
∵四边形ABCD是正方形,
∴,
∵,
∴,
∴.
∴的值为.
20.(1)连接AC、BD,
∵ E,F分别是AB、BC的中点,
∴EF// AC, EF=AC,
同理HG∥AC,GH =AC,
∴EF// HG, EF= HG,
∴四边形EFGH是平行四边形;
(2)当AC = BD时,四边形EFGH是菱形,
∵G、H是CD和AD的中点,
∴GH=AC,GH//AC
∵EH=BD,
∴GH = EH,
又∵四边形EFGH是平行四边形,
∴四边形EFGH是菱形;
(3)AC⊥BD,平行四边形EFGH就是矩形.
∵E、F、G、H分别是AB、BC、CD、DA的中点,
∴EH//BD, FG// BD,EF//AC,HG// AC;
当AC⊥BD时,
∵EH∥BD,FG∥BD,EF∥AC,HG// AC;
∴.EH⊥EF,EF⊥GF,HG⊥FG,HG⊥EH,
∴∠GHE=∠HEF=∠EFG=90°
∴EFGH就是矩形.
(4)当AC= BD且AC⊥BD时,四边形EFGH是正方形,
∵AC⊥BD,GH//AC,
∴GH⊥BD,
∵EH//BD,
∴GH⊥EH,
又∵四边形EFGH是菱形,
∴四边形EFGH是正方形;
故答案为: AC= BD且AC⊥BD.
21.(1)∵△DAE逆时针旋转90°得到△DCM,
∴DE=DM ,∠EDM=90°,
∴∠EDF + ∠FDM=90°,
∵∠EDF=45°,
∴∠FDM =∠EDM=45°,
∵ DF= DF,
∴△DEF≌△DMF,
∴ EF=MF
(2) 设EF=x,
∵AE=CM=1 ,
∴ BF=BM-MF=BM-EF=4-x,
∵ EB=2,
在Rt△EBF中,由勾股定理得,
即,
解得,.
