1.4 .3空间立体几何向量与夹角 测试练习题(含答案)
文档属性
| 名称 | 1.4 .3空间立体几何向量与夹角 测试练习题(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 685.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-13 09:34:15 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
2.4.3-1 空间向量与夹角测试练习题
班级:_________ 姓名:___________
一、选择题
1.已知异面直线的方向向量分别是,则夹角的大小是( )
A. B. C. D.
2.已知向量分别是直线l与平面α的方向向量、法向量,若cos〈〉=-,则l与α所成的角为( )
A.30° B.60° C.150° D.120°
3.在直三棱柱中,若,,,,M为的中点,P为BM的中点,Q在线段上,.则异面直线PQ与AC所成角的余弦值为( )
A. B. C. D.
4.在三棱锥中,平面,,,,分别是棱,,的中点,,,则直线与平面所成角的正弦值为( )
A. B. C. D.
5.(多选)将正方形沿对角线折成直二面角,则下列结论正确的是( )
A. B.是等边三角形
C.与平面所成的角为90° D.与所成的角为30°
6.(多选)在直三棱柱中,,,分别是的中点,在线段上,则下面说法中正确的有( )
A.平面 B.若是上的中点,则
C.直线与平面所成角的正弦值为
D.直线与直线所成角最小时,线段长为
二、填空题
7.三棱锥中,底面为等腰直角三角形,且,平面,,分别是,的中点,则直线与所成的角的正弦值为___________.
8. 和所在平面垂直,且,,则直线与平面所成的角的大小为________.
三、解答题
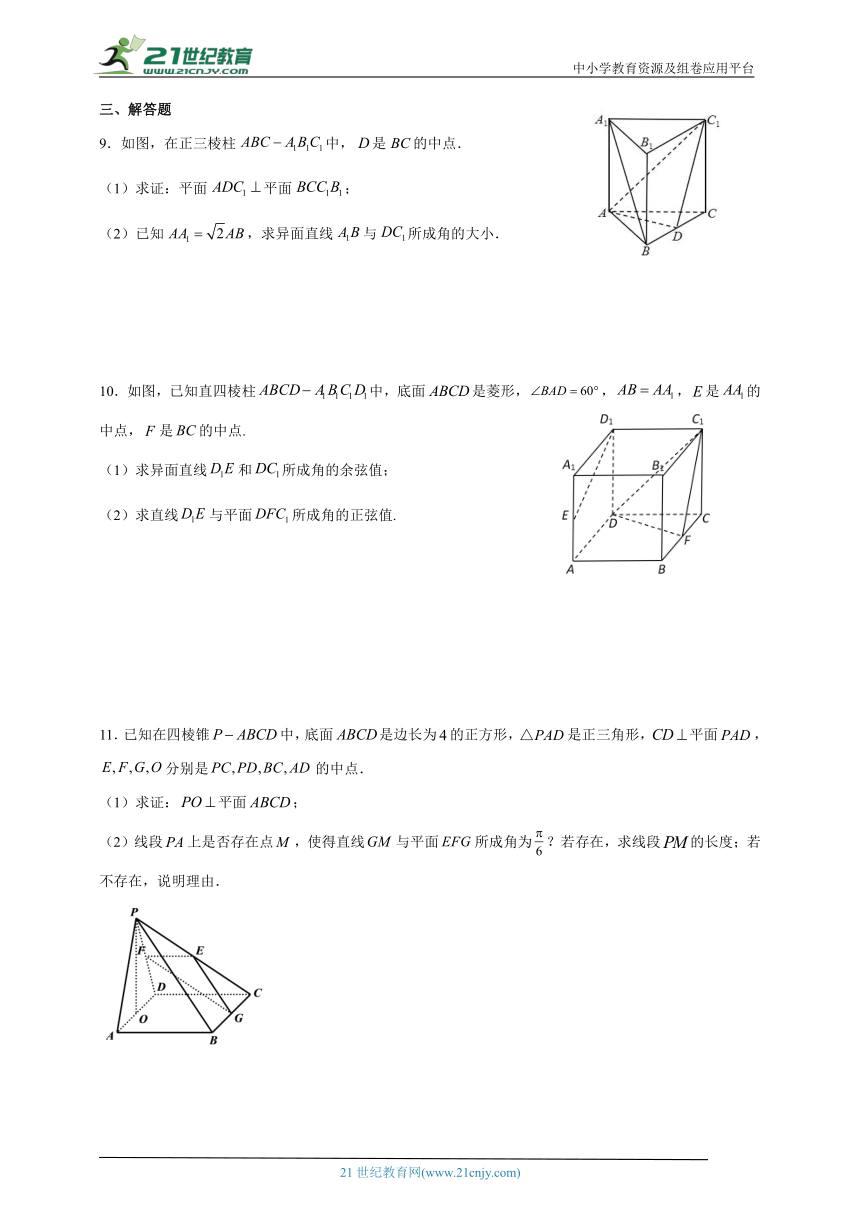
9.如图,在正三棱柱中,是的中点.
(1)求证:平面平面;
(2)已知,求异面直线与所成角的大小.
10.如图,已知直四棱柱中,底面是菱形,,,是的中点,是的中点.
(1)求异面直线和所成角的余弦值;
(2)求直线与平面所成角的正弦值.
11.已知在四棱锥中,底面是边长为的正方形,是正三角形,平面,分别是的中点.
(1)求证:平面;
(2)线段上是否存在点,使得直线与平面所成角为?若存在,求线段的长度;若不存在,说明理由.
参考答案
1~4 CBDB 5. AB 6. ACD
7. 8.
9. 解:(1)因为正三棱柱,所以,又因为是的中点,所以,又因为平面平面,且平面平面,所以平面,又因为平面,所以平面平面;
(2)取的中点,连接,由正三棱柱的几何特征可知两两垂直,故以为坐标原点,分以所在直线为轴,轴,轴建立如图所示空间直角坐标系,设,则,所以,则
所以
由于异面直线成角的范围是,所以异面直线与所成角的余弦值为,因此异面直线与所成角为.
10. (1)解:连结,使.因为底面是菱形,所以,
以为原点,的方向为轴 轴的正方向,以四棱柱上下底面的中心连线指向上底面的方向为轴正方向,建立空间直角坐标系,如图所示.
设,由,底面是菱形,所以.
所以
,,,,
是的中点,是的中点,,
设异面直线和所成角为,则.
异面直线和所成角的余弦值为.
(2)解:由(1)可得,
设平面的法向量为,则
,令,得,
由(1)知,设直线与平面所成角为,则. 直线与平面所成角的正弦值为.
11. 解:(1)为正三角形,为中点,;
平面,平面,;
平面,,平面;
(2)连接,则,,
则以为原点,为轴,可建立如图所示的空间直角坐标系,
则,,,,,
,,,
设线段上是否存在点,使得直线与平面所成角为,且,
,,;
设平面的法向量,
则,令,则,,,
,
整理可得:,方程无解,不存在这样的点.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
2.4.3-1 空间向量与夹角测试练习题
班级:_________ 姓名:___________
一、选择题
1.已知异面直线的方向向量分别是,则夹角的大小是( )
A. B. C. D.
2.已知向量分别是直线l与平面α的方向向量、法向量,若cos〈〉=-,则l与α所成的角为( )
A.30° B.60° C.150° D.120°
3.在直三棱柱中,若,,,,M为的中点,P为BM的中点,Q在线段上,.则异面直线PQ与AC所成角的余弦值为( )
A. B. C. D.
4.在三棱锥中,平面,,,,分别是棱,,的中点,,,则直线与平面所成角的正弦值为( )
A. B. C. D.
5.(多选)将正方形沿对角线折成直二面角,则下列结论正确的是( )
A. B.是等边三角形
C.与平面所成的角为90° D.与所成的角为30°
6.(多选)在直三棱柱中,,,分别是的中点,在线段上,则下面说法中正确的有( )
A.平面 B.若是上的中点,则
C.直线与平面所成角的正弦值为
D.直线与直线所成角最小时,线段长为
二、填空题
7.三棱锥中,底面为等腰直角三角形,且,平面,,分别是,的中点,则直线与所成的角的正弦值为___________.
8. 和所在平面垂直,且,,则直线与平面所成的角的大小为________.
三、解答题
9.如图,在正三棱柱中,是的中点.
(1)求证:平面平面;
(2)已知,求异面直线与所成角的大小.
10.如图,已知直四棱柱中,底面是菱形,,,是的中点,是的中点.
(1)求异面直线和所成角的余弦值;
(2)求直线与平面所成角的正弦值.
11.已知在四棱锥中,底面是边长为的正方形,是正三角形,平面,分别是的中点.
(1)求证:平面;
(2)线段上是否存在点,使得直线与平面所成角为?若存在,求线段的长度;若不存在,说明理由.
参考答案
1~4 CBDB 5. AB 6. ACD
7. 8.
9. 解:(1)因为正三棱柱,所以,又因为是的中点,所以,又因为平面平面,且平面平面,所以平面,又因为平面,所以平面平面;
(2)取的中点,连接,由正三棱柱的几何特征可知两两垂直,故以为坐标原点,分以所在直线为轴,轴,轴建立如图所示空间直角坐标系,设,则,所以,则
所以
由于异面直线成角的范围是,所以异面直线与所成角的余弦值为,因此异面直线与所成角为.
10. (1)解:连结,使.因为底面是菱形,所以,
以为原点,的方向为轴 轴的正方向,以四棱柱上下底面的中心连线指向上底面的方向为轴正方向,建立空间直角坐标系,如图所示.
设,由,底面是菱形,所以.
所以
,,,,
是的中点,是的中点,,
设异面直线和所成角为,则.
异面直线和所成角的余弦值为.
(2)解:由(1)可得,
设平面的法向量为,则
,令,得,
由(1)知,设直线与平面所成角为,则. 直线与平面所成角的正弦值为.
11. 解:(1)为正三角形,为中点,;
平面,平面,;
平面,,平面;
(2)连接,则,,
则以为原点,为轴,可建立如图所示的空间直角坐标系,
则,,,,,
,,,
设线段上是否存在点,使得直线与平面所成角为,且,
,,;
设平面的法向量,
则,令,则,,,
,
整理可得:,方程无解,不存在这样的点.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
