平行四边形的判定[下学期]
图片预览





文档简介
课件32张PPT。第三章 平行四边形平行四边形的判定复习定理1:平行四边形的对边平行.
定理2:平行四边形的对边相等.
定理3:平行四边形的对角相等.
定理4:平行四边形的对角线互相平分.
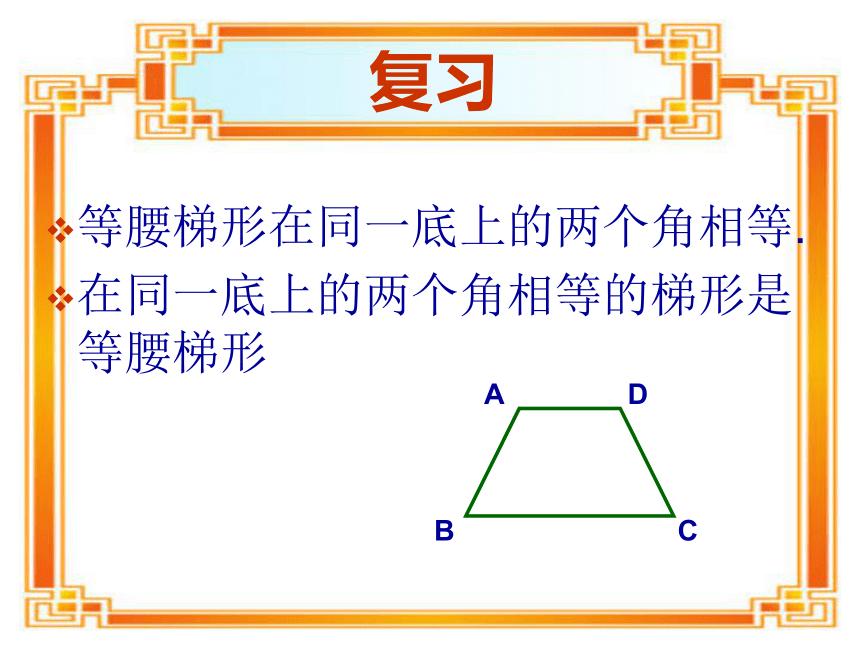
定理5:夹在平行线间的平行线段相等.平行四边形的性质复习等腰梯形在同一底上的两个角相等.
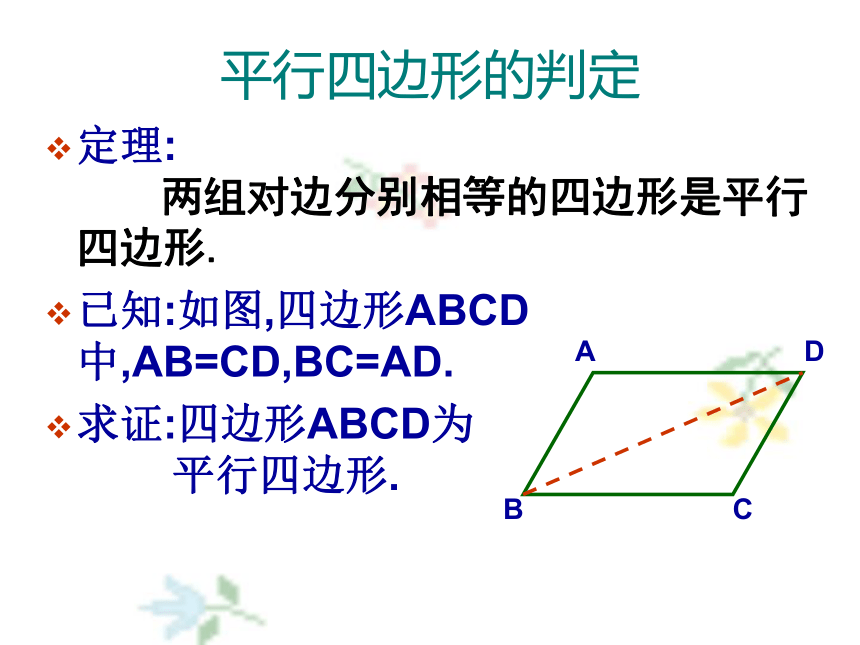
在同一底上的两个角相等的梯形是等腰梯形怎样得到平行四边形?由定义判定: 两组对边分别平行的四边形叫做平行四边形.平行四边形的判定定理: 两组对边分别相等的四边形是平行四边形.
已知:如图,四边形ABCD中,AB=CD,BC=AD.
求证:四边形ABCD为 平行四边形.议一议定理:一组对边平行且相等的
四边形为平行四边形.
一组对边平行且相等的四边形是平行四边形吗?请证明你的结论.
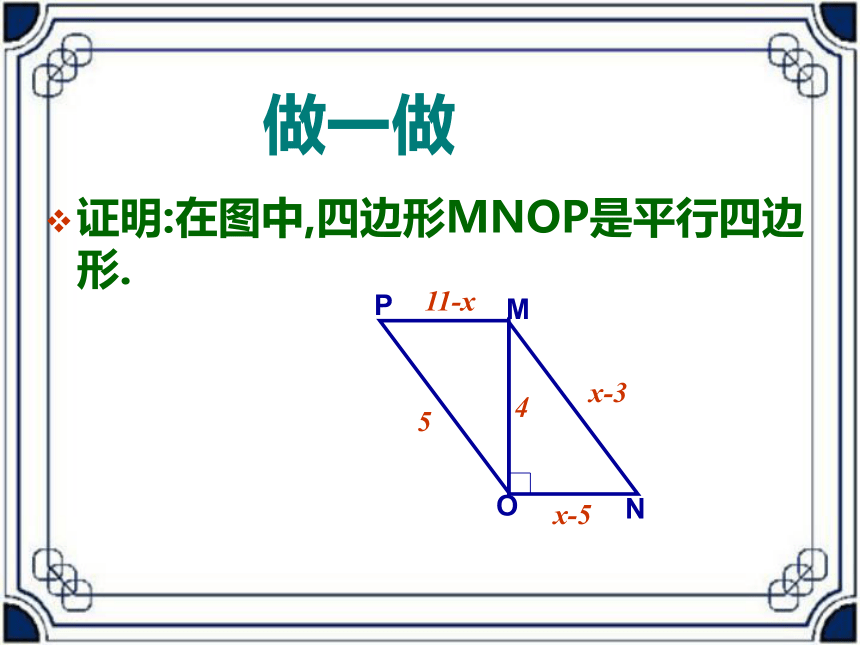
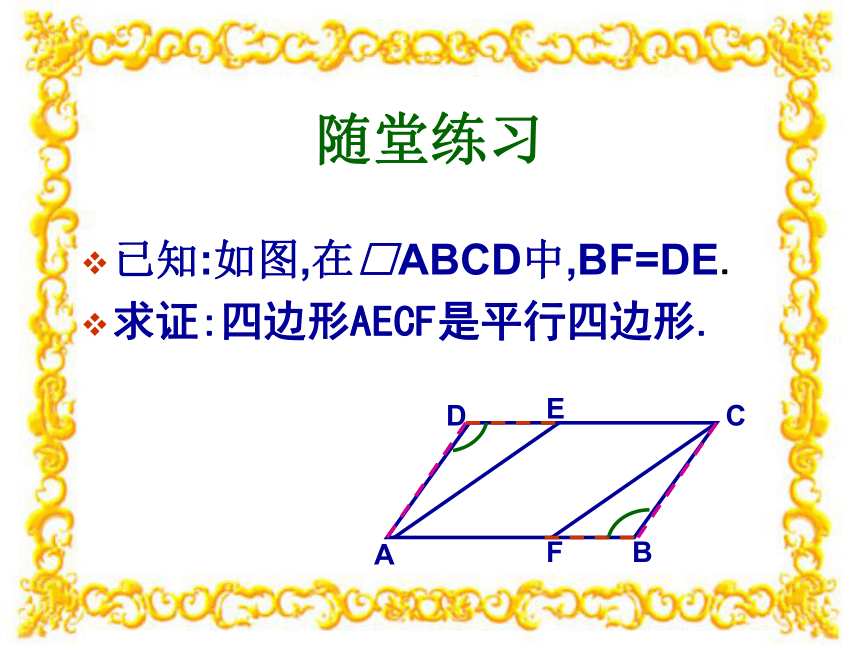
做一做证明:在图中,四边形MNOP是平行四边形.随堂练习已知:如图,在□ABCD中,BF=DE.
求证:四边形AECF是平行四边形.
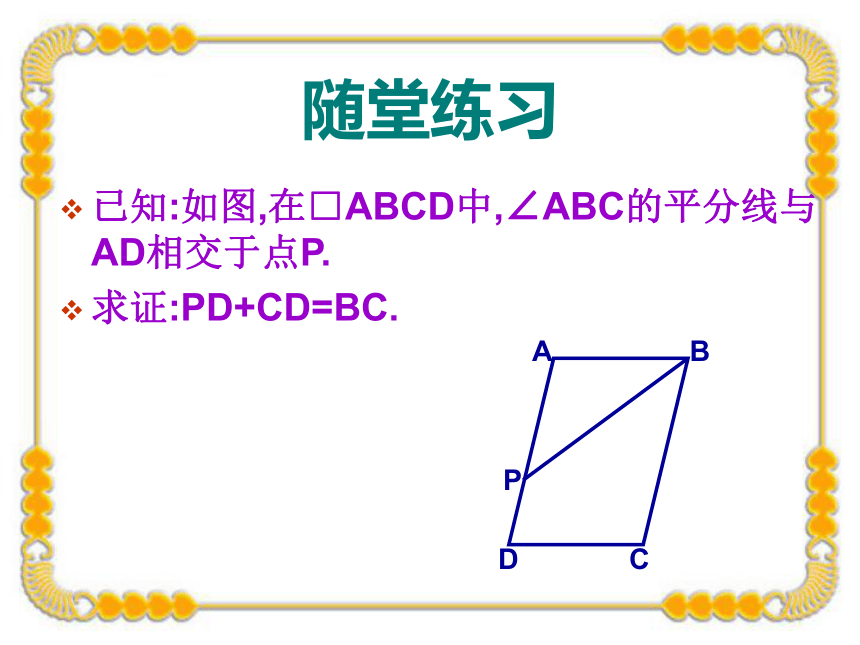
已知:如图,在□ABCD中,∠ABC的平分线与AD相交于点P.
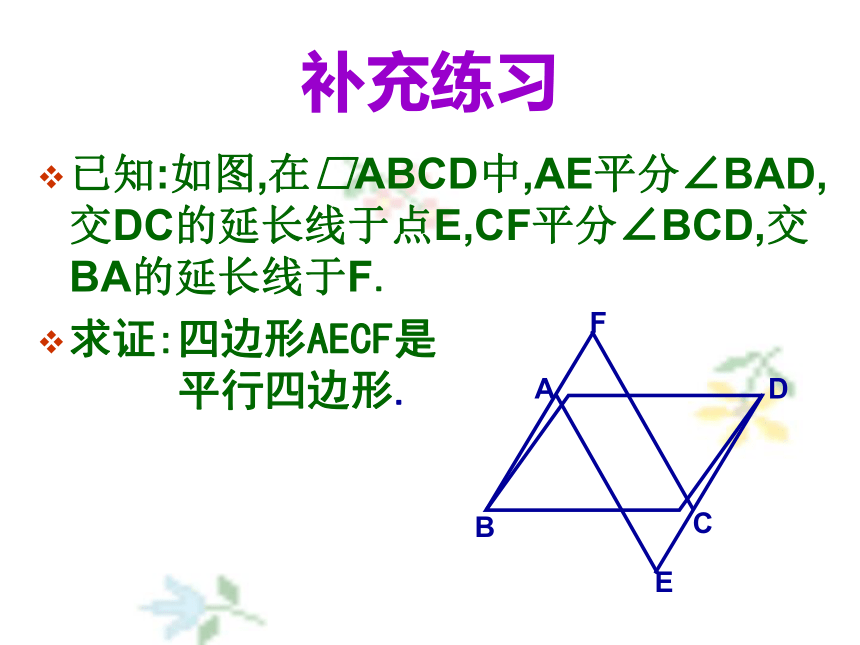
求证:PD+CD=BC.随堂练习已知:如图,在□ABCD中,AE平分∠BAD,交DC的延长线于点E,CF平分∠BCD,交BA的延长线于F.
求证:四边形AECF是 平行四边形.
补充练习例题2 已知:ABCD中,E、F分别是边AD、
BC的中点
求证:EB=DFABCD 利用平行四边形的性质,对边
平行且相等,结合线段的中点
定义,根据判定定理4进行解题
证明: ∵ 四边形ABCD是
平行 四边形
∴AD=BC AD ∥ BC
∵ ED= AD /2 BF= BC/2
∴ ED=BF ED∥BF
∴四边形EBFD是平行四边形
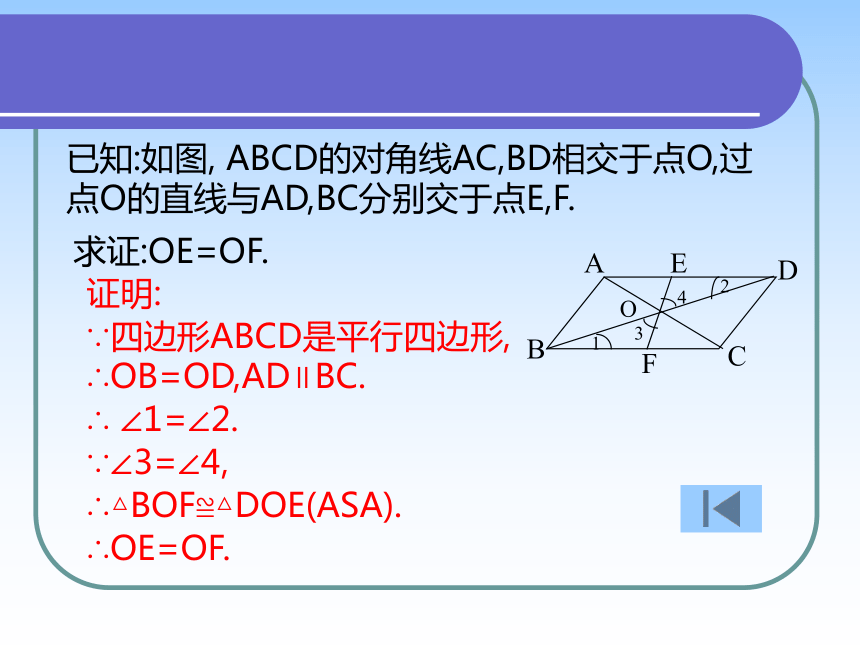
∴ EB=DFEF已知:如图, ABCD的对角线AC,BD相交于点O,过点O的直线与AD,BC分别交于点E,F.求证:OE=OF.证明:∴OB=OD,AD∥BC.∴ ∠1=∠2.∵∠3=∠4,∴△BOF≌△DOE(ASA).∴OE=OF.∵四边形ABCD是平行四边形,19.1.2平行四边形的判定(2)复习定理:两组对边分别平行的四边形是
平行四边形.
定理:两组对边分别相等的四边形是
平行四边形.
定理:一组对边平行且相等的四边形
是平行四边形.BDAC∠A+ ∠B=180 ° AD∥BC 小锋提议:我们可以度量它的角,如果它的两组对角分别相等,那么它就是一个平行四边形。已知:四边形ABCD,
∠A=∠C,∠B=∠D
求证:四边形ABCD是
平行四边形ABCD∠A+ ∠D=180 ° AB∥CD∠A+ ∠B +∠C+ ∠D =360 °BDAC已知:四边形ABCD, ∠A=∠C,∠B=∠D
求证:四边形ABCD是平行四边形∵∠A=∠C,∠B=∠D(已知)
又∵∠A+ ∠B+ ∠C+ ∠D =360 °
∴ 2∠A+ 2∠B=360 °证明:即∠A+ ∠B=180 °
∴ AD∥BC (同旁内角互补,两直线平行)同理可证AB∥CD
∴四边形ABCD是平行四边形平行四边形判定平行四边形的判定定理:
两组对角分别相等的四边形是平行四边形。 ∵ ∠A=∠C, ∠B=∠D (已知)
∴四边形ABCD是平行四边形(两 组对角分别相等的四边形是平行四边形。) 小丽却说:“我可以不用任何作图工具,只要两条细绳就能判断它是不是平行四边形。”
只见小丽用两条细绳做四边形的对角线,并在两条对角线的交点处作了个记号。然后分别把两条对角线沿记号点对折,发现它们被记号点分成的两段线段都能重合,小丽高兴地说:“这的确是个平行四边形!”你认为小丽的做法有根据吗?已知:四边形ABCD, AC、BD交于点O
且OA=OC,OB=OD
求证:四边形ABCD是平行四边形试一试证明:∵ AO = CO ,BO = DO ,∠1 = ∠2∴△AOB≌△COD∴AB ∥ CD 同理AD ∥ BC∴四边形ABCD是平行四边形
(两组对边分别平行的四边形是平行四边形)∴ ∠3 = ∠4平行四边形判定平行四边形的判定定理:
对角线互相平分的四边形是平行四边形。 ∵ OA=OC,OB=OD(已知)
∴四边形ABCD是平行四边形(对角线互相平分的四边形是平行四边形。) 请你识别下列四边形哪些是平行四边形?说一说⑴⑷
⑶ABCD120°60°5㎝5㎝BADC4.8㎝4.8㎝⑵7.6㎝7.6㎝大显身手已知:E、F是平行四边形ABCD对角线 AC上的两点,并且AE=CF。
求证:四边形BFDE是平行四边形DOABCEF证明:作对角线BD,交AC于点O。
∵四边形ABCD是平行四边形
∴ AO=CO,BO=DO
∵AE=CF
∴AO-AE=CO-CF
∴EO=FO
又 BO=DO
∴ 四边形BFDE是平行四边形
例1:求证顺次连结四边形各边中点所得的四边形是平行四边形。已知:E、F、G、H分别是四边形ABCD中AB、
BC、CD、DA的中点。
求证:四边形EFGH是平行四边形。 任意四边形四边中点连线所得的四边形一定是平行四边形。练一练:1、已知在平行四边形ABCD中,E、G分别在AB、CD上,H、F在对角线上,且AE=CG ,AH=CF, 求证:四边形EFGH为平行四边形 2、已知:AD为△ABC的角平分线,DE∥AB ,在AB上截取BF=AE。
求证:EF=BD
123
3、已知 平行四边形 ABCD中,直线MN // AC,分别交DA延长线于M,DC延长线于N,AB于P,BC于Q。
求证:PM=QN。4、下列条件中,不能判定四边形ABCD是平行四边形的是( )
A、∠A=∠C,∠B=∠D
∠A=∠B=∠C=90
∠A+∠B=180 ,∠B+∠C=180
∠A+∠B=180 ,∠C+∠D=180D5、下列条件中能判定一个四边形是平行四边形的条件是( )
①一组对边相等,且一组对角相等,②一组对边相等且一条对角线平分另一条对角线,③一组对角相等,且这一组对角的顶点所连结的对角线被另一条对角线平分,④一组对角相等,且这一组对角的顶点所连结的对角线平分这组对角。
A、①和② B、②和③
C、②和④ D、只有④D 如图,在 ?ABCD中,已知两条对角线相交于
点O,E、F、G、H分别是AO、BO、CO、DO的中点,
以图中的点为顶点,尽可能多地画出平行四边形。画一画ADCBEFGHO两组对边分别相等两组对角分别相等对角线互相平分两组对边分别平行一组对边平行且相等四边形是平行四边形边角对角线:平行四边形的判定方法共有几种? 作业:
定理2:平行四边形的对边相等.
定理3:平行四边形的对角相等.
定理4:平行四边形的对角线互相平分.
定理5:夹在平行线间的平行线段相等.平行四边形的性质复习等腰梯形在同一底上的两个角相等.
在同一底上的两个角相等的梯形是等腰梯形怎样得到平行四边形?由定义判定: 两组对边分别平行的四边形叫做平行四边形.平行四边形的判定定理: 两组对边分别相等的四边形是平行四边形.
已知:如图,四边形ABCD中,AB=CD,BC=AD.
求证:四边形ABCD为 平行四边形.议一议定理:一组对边平行且相等的
四边形为平行四边形.
一组对边平行且相等的四边形是平行四边形吗?请证明你的结论.
做一做证明:在图中,四边形MNOP是平行四边形.随堂练习已知:如图,在□ABCD中,BF=DE.
求证:四边形AECF是平行四边形.
已知:如图,在□ABCD中,∠ABC的平分线与AD相交于点P.
求证:PD+CD=BC.随堂练习已知:如图,在□ABCD中,AE平分∠BAD,交DC的延长线于点E,CF平分∠BCD,交BA的延长线于F.
求证:四边形AECF是 平行四边形.
补充练习例题2 已知:ABCD中,E、F分别是边AD、
BC的中点
求证:EB=DFABCD 利用平行四边形的性质,对边
平行且相等,结合线段的中点
定义,根据判定定理4进行解题
证明: ∵ 四边形ABCD是
平行 四边形
∴AD=BC AD ∥ BC
∵ ED= AD /2 BF= BC/2
∴ ED=BF ED∥BF
∴四边形EBFD是平行四边形
∴ EB=DFEF已知:如图, ABCD的对角线AC,BD相交于点O,过点O的直线与AD,BC分别交于点E,F.求证:OE=OF.证明:∴OB=OD,AD∥BC.∴ ∠1=∠2.∵∠3=∠4,∴△BOF≌△DOE(ASA).∴OE=OF.∵四边形ABCD是平行四边形,19.1.2平行四边形的判定(2)复习定理:两组对边分别平行的四边形是
平行四边形.
定理:两组对边分别相等的四边形是
平行四边形.
定理:一组对边平行且相等的四边形
是平行四边形.BDAC∠A+ ∠B=180 ° AD∥BC 小锋提议:我们可以度量它的角,如果它的两组对角分别相等,那么它就是一个平行四边形。已知:四边形ABCD,
∠A=∠C,∠B=∠D
求证:四边形ABCD是
平行四边形ABCD∠A+ ∠D=180 ° AB∥CD∠A+ ∠B +∠C+ ∠D =360 °BDAC已知:四边形ABCD, ∠A=∠C,∠B=∠D
求证:四边形ABCD是平行四边形∵∠A=∠C,∠B=∠D(已知)
又∵∠A+ ∠B+ ∠C+ ∠D =360 °
∴ 2∠A+ 2∠B=360 °证明:即∠A+ ∠B=180 °
∴ AD∥BC (同旁内角互补,两直线平行)同理可证AB∥CD
∴四边形ABCD是平行四边形平行四边形判定平行四边形的判定定理:
两组对角分别相等的四边形是平行四边形。 ∵ ∠A=∠C, ∠B=∠D (已知)
∴四边形ABCD是平行四边形(两 组对角分别相等的四边形是平行四边形。) 小丽却说:“我可以不用任何作图工具,只要两条细绳就能判断它是不是平行四边形。”
只见小丽用两条细绳做四边形的对角线,并在两条对角线的交点处作了个记号。然后分别把两条对角线沿记号点对折,发现它们被记号点分成的两段线段都能重合,小丽高兴地说:“这的确是个平行四边形!”你认为小丽的做法有根据吗?已知:四边形ABCD, AC、BD交于点O
且OA=OC,OB=OD
求证:四边形ABCD是平行四边形试一试证明:∵ AO = CO ,BO = DO ,∠1 = ∠2∴△AOB≌△COD∴AB ∥ CD 同理AD ∥ BC∴四边形ABCD是平行四边形
(两组对边分别平行的四边形是平行四边形)∴ ∠3 = ∠4平行四边形判定平行四边形的判定定理:
对角线互相平分的四边形是平行四边形。 ∵ OA=OC,OB=OD(已知)
∴四边形ABCD是平行四边形(对角线互相平分的四边形是平行四边形。) 请你识别下列四边形哪些是平行四边形?说一说⑴⑷
⑶ABCD120°60°5㎝5㎝BADC4.8㎝4.8㎝⑵7.6㎝7.6㎝大显身手已知:E、F是平行四边形ABCD对角线 AC上的两点,并且AE=CF。
求证:四边形BFDE是平行四边形DOABCEF证明:作对角线BD,交AC于点O。
∵四边形ABCD是平行四边形
∴ AO=CO,BO=DO
∵AE=CF
∴AO-AE=CO-CF
∴EO=FO
又 BO=DO
∴ 四边形BFDE是平行四边形
例1:求证顺次连结四边形各边中点所得的四边形是平行四边形。已知:E、F、G、H分别是四边形ABCD中AB、
BC、CD、DA的中点。
求证:四边形EFGH是平行四边形。 任意四边形四边中点连线所得的四边形一定是平行四边形。练一练:1、已知在平行四边形ABCD中,E、G分别在AB、CD上,H、F在对角线上,且AE=CG ,AH=CF, 求证:四边形EFGH为平行四边形 2、已知:AD为△ABC的角平分线,DE∥AB ,在AB上截取BF=AE。
求证:EF=BD
123
3、已知 平行四边形 ABCD中,直线MN // AC,分别交DA延长线于M,DC延长线于N,AB于P,BC于Q。
求证:PM=QN。4、下列条件中,不能判定四边形ABCD是平行四边形的是( )
A、∠A=∠C,∠B=∠D
∠A=∠B=∠C=90
∠A+∠B=180 ,∠B+∠C=180
∠A+∠B=180 ,∠C+∠D=180D5、下列条件中能判定一个四边形是平行四边形的条件是( )
①一组对边相等,且一组对角相等,②一组对边相等且一条对角线平分另一条对角线,③一组对角相等,且这一组对角的顶点所连结的对角线被另一条对角线平分,④一组对角相等,且这一组对角的顶点所连结的对角线平分这组对角。
A、①和② B、②和③
C、②和④ D、只有④D 如图,在 ?ABCD中,已知两条对角线相交于
点O,E、F、G、H分别是AO、BO、CO、DO的中点,
以图中的点为顶点,尽可能多地画出平行四边形。画一画ADCBEFGHO两组对边分别相等两组对角分别相等对角线互相平分两组对边分别平行一组对边平行且相等四边形是平行四边形边角对角线:平行四边形的判定方法共有几种? 作业:
