21.2.3因式分解法

课件35张PPT。义务教育课程标准实验教科书九年级 上册人民教育出版社21.2.3 因式分解法温故而知新1.我们已经学过了几种解一元二次方程 的方法?2.什么叫分解因式? 把一个多项式分解成几个整式乘积
的形式叫做分解因式.直接开平方法配方法x2=a (a≥0)(x+m)2=n (n≥0)公式法分解因式的方法有那些?（1）提取公因式法:（2）公式法:（3）十字相乘法:am+bm+cm=m(a+b+c).a2-b2=(a+b)(a-b), a2±2ab+b2=(a±b)2.x2+(a+b)x+ab=(x+a)(x+b). 根据物理学规律，如果把一个物体从地面 10 m/s 的速度竖直上抛，那么经过 x s 物体离地面的高度（单位：m）为 设物体经过 x s 落回地面，这时它离地面的高度为 0 ，即 根据这个规律求出物体经过多少秒落回地面？（精确到 0.01 s）解：配方法公式法解：a = 4.9，b =－10，c = 0 b2－4ac
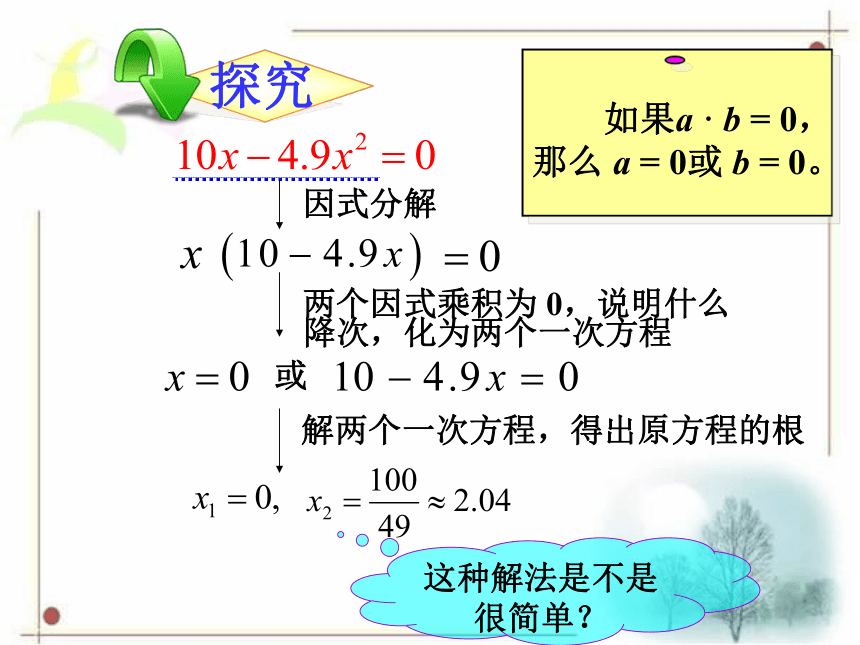
= (－10)2－4×4.9×0=100因式分解 如果a · b = 0，那么 a = 0或 b = 0。两个因式乘积为 0，说明什么或降次，化为两个一次方程解两个一次方程，得出原方程的根这种解法是不是很简单？可以发现，上述解法中，由①到②的过程，不是用开方降次，而是先因式分解使方程化为两个一次式的乘积等于0的形式，再使这两个一次式分别等于0，从而实现降次，这种解法叫做因式分解法．以上解方程 的方法是如何使二次方程降为一次的？①②讨论 以上解方程①的方法是如何使二次方程降为一次的? 可以发现,上述解法中,由①到②的过程,不是用开平方降次,而是先因式分解使方程化为两个一次式的乘积等于0的形式,再使这两个一次式分别等于0,从而实现降次.这种解法叫做因式分解法.提示:
1.用分解因式法的条件是:方程左边易于分解,而右边等于零;
2.关键是熟练掌握因式分解的知识;
3.理论依旧是“ab=0,则a=0或b=0 ”分解因式法解一元二次方程的步骤是:2. 将方程左边因式分解为A×B;3. 根据“ab=0,则a=0或b=0”,转化为两个一元一次方程.4. 分别解这两个一元一次方程，它们的根就是原方程的根.1.将方程右边等于0;例3 解下列方程：解：（1）因式分解，得于是得x－2＝0或x＋1=0,x1=2，x2=－1.(2)移项、合并同类项，得因式分解，得 ( 2x＋1)( 2x－1 )=0.于是得2x＋1=0或2x－1=0,(x－2)(x＋1)=0.1.解下列方程：解： 因式分解，得（1） x2+x=0x ( x+1 ) = 0.得 x = 0 或 x + 1 =0，x1=0 , x2=－1.解：因式分解，得练习解：化为一般式为因式分解，得x2－2x+1 = 0.( x－1 )( x－1 ) = 0.有 x － 1 = 0 或 x － 1 = 0，x1=x2=1.解：因式分解，得( 2x + 11 )( 2x－ 11 ) = 0.有 2x + 11 = 0 或 2x － 11= 0，解：化为一般式为因式分解，得6x2 － x －2 = 0.( 3x － 2 )( 2x + 1 ) = 0.有 3x － 2 = 0 或 2x + 1 = 0，解：变形有因式分解，得( x －4 ) 2 － ( 5 － 2x )2=0.( x － 4 － 5 + 2x )( x － 4 + 5 －2x ) = 0.( 3x － 9 )( 1 － x ) = 0.有 3x － 9 = 0 或 1 － x = 0，x1 = 3 , x2 = 1.2.把小圆形场地的半径增加5m得到大圆形场地，场地面积增加了一倍，求小圆形场地的半径．解：设小圆形场地的半径为r根据题意 ( r + 5 )2×π=2r2π.因式分解，得于是得答：小圆形场地的半径是分解因式法解一元二次方程的步骤是:1. 将方程左边因式分解，右边等于0;2. 根据“至少有一个因式为零”,转化为两个一元一次方程.3. 分别解两个一元一次方程，它们的根就是原方程的根.小结: 用因式分解法解一元二次方程的步骤 1. 方程右边化为______。
2. 将方程左边分解成两个___________的乘积。
3. 至少________因式为零，得到两个一元一次方程。
4. 两个___________________就是原方程的根。 零一次因式有一个一元一次方程的解AB = 0（ A、B 表示两个因式）A = 0 或 B = 0（2）（3）x2－4 = 0（4）(3x＋1)2－5 = 0 （1）2x2－4x ＋2 = 0（1）2x2－4x ＋2 = 0∴ x1 = 解：因式分解，得2 (x－1) 2x－1 = 0= 0或x2 = 1x－1 = 0分解因式的方法有那些?（1）提取公因式法:（2）公式法:am+bm+cm=m(a+b+c).a2-b2=(a+b)(a-b), a2±2ab+b2=(a±b)2.（2）解：移项，得因式分解，得x＋2 = 0或3x－5 = 0∴ x1 =－2 ，x2 =（3）x2－4 = 0解：因式分解，得(x＋2)x＋2 = 0∴ x1 = －2，(x－2)= 0或x－2 = 0x2 = 2（4）(3x＋1)2－5 = 0 = 0 或解：因式分解，得∴你学过一元二次方程的哪些解法?说一说因式分解法开平方法配方法公式法你能说出每一种解法的特点吗?方程的左边是完全平方式,右边是非负数;即形如x2=a(a≥0)开平方法1.化1:把二次项系数化为1;2.移项:把常数项移到方程的右边;3.配方:方程两边同加一次项系数 一半的平方;4.变形:化成5.开平方，求解“配方法”解方程的基本步骤★一除、二移、三配、四化、五解.用公式法解一元二次方程的前提是:公式法1.必需是一般形式的一元二次方程:
ax2+bx+c=0(a≠0).
2.b2-4ac≥0.
1.用因式分解法的条件是:方程左边能够
分解,而右边等于零;因式分解法2.理论依据是:如果两个因式的积等于零
那么至少有一个因式等于零.因式分解法解一元二次方程的一般步骤:一移-----方程的右边=0;二分-----方程的左边因式分解;三化-----方程化为两个一元一次方程;四解-----写出方程两个解;请用四种方法解下列方程:
4(x＋1)2 = (2x－5)2比一比结论先考虑开平方法,
再用因式分解法;
最后才用公式法和配方法;3.公式法：总结：方程中有括号时，应先用整体思想考虑有没有简单方法，若看不出合适的方法时，则把它去括号并整理为一般形式再选取合理的方法。
① x2-3x+1=0 ② 3x2-1=0
③ -3t2+t=0 ④ x2-4x=2
⑤ 2x2－x=0 ⑥ 5(m+2)2=8
⑦ 3y2-y-1=0 ⑧ 2x2+4x-1=0
⑨ (x-2)2=2(x-2)
适合运用直接开平方法 ；
适合运用因式分解法 ；
适合运用公式法 ；
适合运用配方法 .
一般地，当一元二次方程一次项系数为0时（ax2+c=0），应选用直接开平方法；
若常数项为0（ ax2+bx=0），应选用因式分解法；
若一次项系数和常数项都不为0 (ax2+bx+c=0），先化为一般式，看一边的整式是否容易因式分解，若容易，宜选用因式分解法，不然选用公式法；
不过当二次项系数是1，且一次项系数是偶数时，用配方法也较简单。我的发现用最好的方法求解下列方程
1)（3x-2）2-49=0
2)（3x-4）2=（4x-3）2
3) 4y=1－ y2选择适当的方法解下列方程:谁最快选用适当的方法解一元二次方程1.解一元二次方程的方法有：
①因式分解法
②直接开平方法
③公式法
④配方法2.引例：给下列方程选择较简便的方法（运用因式分解法）（运用直接开平方法）（运用配方法）（运用公式法）（运用公式法）（方程一边是0，另一边整式容易因式分解）（ ( )2=C C≥0 ）(化方程为一般式）（二次项系数为1，而一次项系为偶数）② 公式法虽然是万能的，对任何一元二次方程都适用，但不一定是最简单的，因此在解方程时我们首先考虑能否应用“直接开平方法”、“因式分解法”等简单方法，若不行，再考虑公式法（适当也可考虑配方法）小结：ax2+c=0 ====>ax2+bx=0 ====>ax2+bx+c=0 ====>因式分解法公式法（配方法）2、公式法虽然是万能的，对任何一元二次方程都适用，但不一定 是最简单的，因此在解方程时我们首先考虑能否应用“直接开平方法”、“因式分解法”等简单方法，若不行，再考虑公式法（适当也可考虑配方法）3、方程中有括号时，应先用整体思想考虑有没有简单方法，若看不出合适的方法时，则把它去括号并整理为一般形式再选取合理的方法。1、直接开平方法因式分解法配方法公式法因式分解法将二次方程化为一元方程降次先配方，再降次直接利用求根公式先使方程一边化为两个一次因式相乘，另一边为0，再分别使各一次因式等于0所有一元二次方程所有一元二次方程某些