鲁教版七年级上册期中检测数学题(含答案)
文档属性
| 名称 | 鲁教版七年级上册期中检测数学题(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 203.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-13 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
七年级数学(上)期中试题
(时间120分钟,满分150分 )
一.选择题(共12小题,每题4分)
1.已知三角形的三边长分别为2、x、2,则x可能是( )
A.5 B.1 C.6 D.4
2.若三角形有两个内角的和是90°,那么这个三角形是( )
A.钝角三角形 B.直角三角形 C.锐角三角形 D.不能确定
3.下列说法:(1)全等图形的形状相同,大小相等;(2)全等三角形的对应边相等
(3)全等图形的周长相等,面积相等;(4)面积相等的两个三角形全等.其中正确的是
A.( 1 )( 3)( 4 ) B.( 2)( 3 )( 4 )
C.( 1 )( 2 )( 3 ) D.( 1 )( 2)( 3 )( 4 )
4.如图,△ACB≌△A′CB′,∠ACB=70°,∠ACB′=100°,则∠BCA′的度数为( )
A.30 B.35° C.40° D.50°
5.如图,AB=DB,∠ABD=∠CBE,①BE=BC,②∠D=∠A,③∠C=∠E,④AC=DE,能使△ABC≌△DBE的条件有( )个.A. 1 B. 2 C.3 D.4
6.下列四个图形中,不是轴对称图形是( )
A. B. C. D.
7.底边上的高为8,底边长为12的等腰三角形的腰长为( )
A.5 B.8 C.10 D.12
8.如图,在△ABC中,AB=AC,∠A=38°,AB的垂直平分线MN交AC于点D,则∠DBC的度数为( )
A.33° B.38° C.43° D.48°
9.如图,在△ABE中,BA=BE,F为AE中点.若∠ABC=34°,∠C=50°,则∠ADB的度数为( )
A.60° B.63° C.67° D.70°
10.如图,在△ABC中,∠C=90°,AC=8,DC=AD,BD平分∠ABC,则点D到AB的距离等于( )
A.4 B.3 C.2 D.1
11.已知一个直角三角形斜边为20,一条直角边长为16,那么它的面积是( )
A.160 B.48 C.60 D.96
12.如图,有一块直角三角形纸片,两直角边AC=6cm,BC=8cm,现将直角边AC沿直线AD折叠,使它落在斜边AB上且与AE重合,则CD等于( )
A.2cm B.3cm C.4cm D.5cm
二.填空题(共6小题 每题4分)
13.已知AD为△ABC的中线,若△ABC的面积为8,则△ABD的面积是 .
14.如图,在3×3的正方形网格中标出了∠1和∠2,则∠1+∠2= °.
15.若等腰三角形的一边是6,另一边是3,则此等腰三角形的周长是 .
16.定义:等腰三角形的顶角与其一个底角的度数的比值k称为这个等腰三角形的“特征值”.若等腰△ABC中,∠A=80°,则它的特征值k= .
17.如图,△ABC中,AB=AC,∠A=40°,点P是△ABC内一点,连结PB、PC,∠1=∠2,则∠BPC的度数是 .
18.一个三角形的三边长的比为3:4:5,且其周长为60cm,则其面积为 .
三、解答题
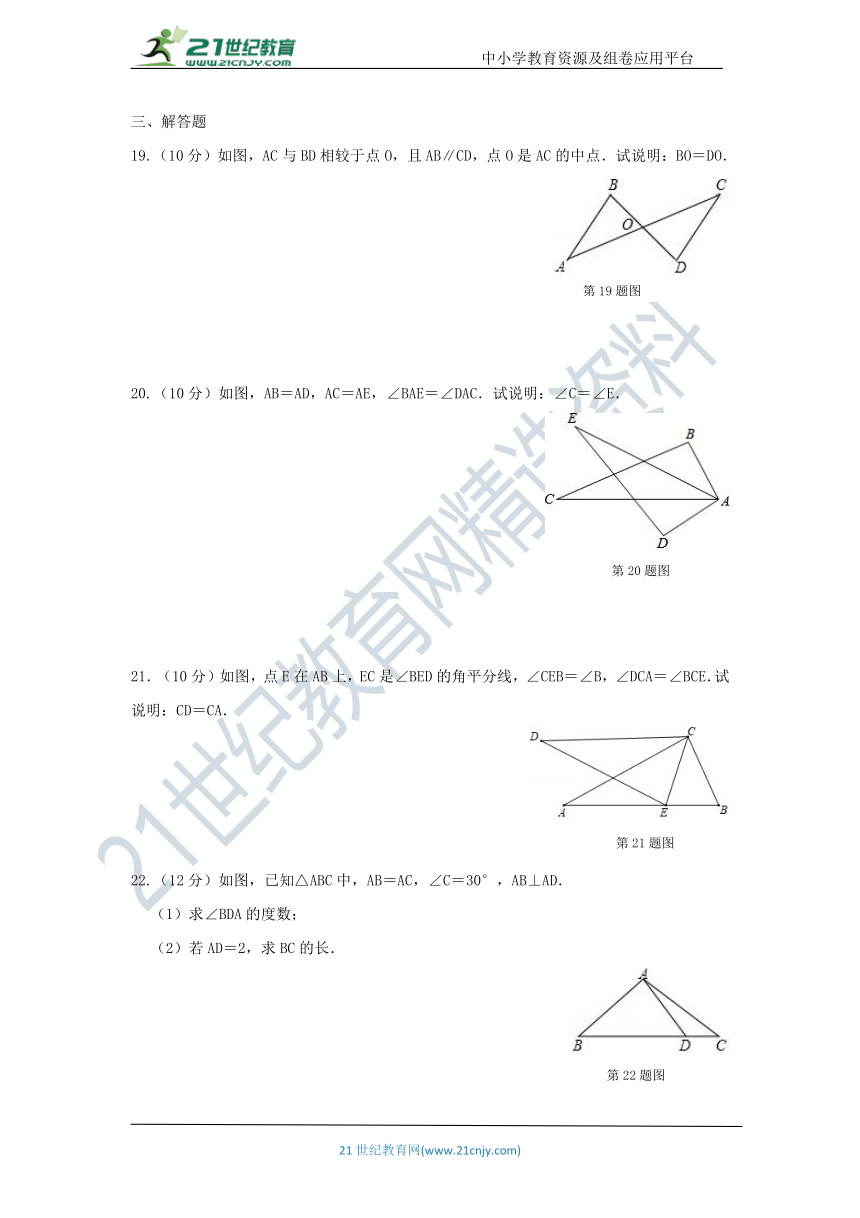
19.(10分)如图,AC与BD相较于点O,且AB∥CD,点O是AC的中点.试说明:BO=DO.
20.(10分)如图,AB=AD,AC=AE,∠BAE=∠DAC.试说明:∠C=∠E.
21.(10分)如图,点E在AB上,EC是∠BED的角平分线,∠CEB=∠B,∠DCA=∠BCE.试说明:CD=CA.
22.(12分)如图,已知△ABC中,AB=AC,∠C=30°,AB⊥AD.
(1)求∠BDA的度数;
(2)若AD=2,求BC的长.
23.(12分)如图,四边形ABCD中,AB=3cm,BC=4cm,CD=12cm,DA=13cm,且∠ABC=90°.求四边形ABCD的面积.
24.(12分)如图,在△ABC中,AB=AC,点O为∠BAC的平分线上一点,连接OB、OC.
(1)试说明:OB=OC;
(2)若OA=OC,∠BAC=46°,求∠OCB的度数.
25.(12分)如图,△ABC为任意三角形,以AB、AC为边分别向外做等边△ABD和等边△ACE,连接CD、BE并相交于点P.试说明:
(1)CD=BE;
(2)∠BPC=120°.
七年级数学(上)期中试题参考答案
一、选择题
1-5 BBCCC 6-10 BCACC 11-12 DB
二、填空题
13.4 14.45 15.15 16. 或
17.110° 18. 150cm2
解答题
19.解:∵AB∥CD,
∴∠A=∠C,∠B=∠D.
∵点O是AC的中点,
∴AO=CO.
在△ABO和△CDO中,,
∴△ABO≌△CDO(AAS),
∴BO=DO.
20.解:∵∠BAE=∠DAC
∴∠BAE+∠CAE=∠DAC+∠CAE
∴∠CAB=∠EAD,且AB=AD,AC=AE
∴△ABC≌△ADE(SAS)
∴∠C=∠E
21.解:∵∠CEB=∠B,
∴CE=CB.
∵EC平分∠BED,
∴∠CED=∠CEB,
∴∠CED=∠B.
∵∠DCA=∠BCE,
∴∠DCE=∠ACB.
在△DCE和△ACB中,
∴△DCE≌△ACB(ASA).
∴CD=CA.
22.解:(1)∵AB=AC
∴∠B=∠C=30°
∵AD⊥AB
∴∠BDA+∠B=90°
∴∠BDA=60°
(2)∵∠BDA=60°,∠C=30°,且∠BDA=∠C+∠DAC
∴∠DAC=60°﹣30°=30°=∠C
∴AD=CD=2
∵AB⊥AD,∠B=30°
∴BD=2AD=4
∵BC=BD+CD
∴BC=2+4=6
23.解:连接AC,
∵∠ABC=90°,AB=4,BC=3,
∴根据勾股定理AC==5(cm),
又∵CD=12cm,AD=13cm,
∴AC2+DC2=52+122=169,
AD2=132=169,
根据勾股定理的逆定理:∠ACD=90°.
∴四边形ABCD的面积=S△ABC+S△ACD=×3×4+×5×12=36(cm2).
24.解:(1)∵OA平分∠BAC,
∴∠BAO=∠CAO=∠BAC.
在△BAO和△CAO中,
,
∴△BAO≌△CAO(SAS)
∴OB=OC.
(2)由(1)得∴∠BAO=∠CAO=∠BAC,OB=OC,
∵OA=OC,
∴OA=OB=OC,
∴∠OAC=∠OCA=∠BAO=∠OBA=23°,
∵∠OCB=∠OAC+∠OCA+∠BAO+∠OBA=2∠BAC=92°.
25.解:(1)∵以AB、AC为边分别向外做等边△ABD和等边△ACE,
∴AD=AB,AE=AC,∠ACE=∠AEC=60°,∠DAB=∠EAC=60°,
∴∠DAB+∠BAC=∠EAC+∠BAC,
∴∠DAC=∠BAE,
在△DAC和△BAE中,
,
∴△DAC≌△BAE(SAS),
∴CD=BE;
(2)∵△DAC≌△BAE,
∴∠BEA=∠ACD,
∴∠BPC=∠ECP+∠PEC
=∠DCA+∠ACE+∠PEC
=∠BEA+∠ACE+∠PEC
=∠ACE+∠AEC
=60°+60°
=120°.
第5题图
第8题图
第4题图图
第14题图
第17题图
第19题图
第20题图
第21题图
第22题图
第23题图
第24题图
第25题图
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
七年级数学(上)期中试题
(时间120分钟,满分150分 )
一.选择题(共12小题,每题4分)
1.已知三角形的三边长分别为2、x、2,则x可能是( )
A.5 B.1 C.6 D.4
2.若三角形有两个内角的和是90°,那么这个三角形是( )
A.钝角三角形 B.直角三角形 C.锐角三角形 D.不能确定
3.下列说法:(1)全等图形的形状相同,大小相等;(2)全等三角形的对应边相等
(3)全等图形的周长相等,面积相等;(4)面积相等的两个三角形全等.其中正确的是
A.( 1 )( 3)( 4 ) B.( 2)( 3 )( 4 )
C.( 1 )( 2 )( 3 ) D.( 1 )( 2)( 3 )( 4 )
4.如图,△ACB≌△A′CB′,∠ACB=70°,∠ACB′=100°,则∠BCA′的度数为( )
A.30 B.35° C.40° D.50°
5.如图,AB=DB,∠ABD=∠CBE,①BE=BC,②∠D=∠A,③∠C=∠E,④AC=DE,能使△ABC≌△DBE的条件有( )个.A. 1 B. 2 C.3 D.4
6.下列四个图形中,不是轴对称图形是( )
A. B. C. D.
7.底边上的高为8,底边长为12的等腰三角形的腰长为( )
A.5 B.8 C.10 D.12
8.如图,在△ABC中,AB=AC,∠A=38°,AB的垂直平分线MN交AC于点D,则∠DBC的度数为( )
A.33° B.38° C.43° D.48°
9.如图,在△ABE中,BA=BE,F为AE中点.若∠ABC=34°,∠C=50°,则∠ADB的度数为( )
A.60° B.63° C.67° D.70°
10.如图,在△ABC中,∠C=90°,AC=8,DC=AD,BD平分∠ABC,则点D到AB的距离等于( )
A.4 B.3 C.2 D.1
11.已知一个直角三角形斜边为20,一条直角边长为16,那么它的面积是( )
A.160 B.48 C.60 D.96
12.如图,有一块直角三角形纸片,两直角边AC=6cm,BC=8cm,现将直角边AC沿直线AD折叠,使它落在斜边AB上且与AE重合,则CD等于( )
A.2cm B.3cm C.4cm D.5cm
二.填空题(共6小题 每题4分)
13.已知AD为△ABC的中线,若△ABC的面积为8,则△ABD的面积是 .
14.如图,在3×3的正方形网格中标出了∠1和∠2,则∠1+∠2= °.
15.若等腰三角形的一边是6,另一边是3,则此等腰三角形的周长是 .
16.定义:等腰三角形的顶角与其一个底角的度数的比值k称为这个等腰三角形的“特征值”.若等腰△ABC中,∠A=80°,则它的特征值k= .
17.如图,△ABC中,AB=AC,∠A=40°,点P是△ABC内一点,连结PB、PC,∠1=∠2,则∠BPC的度数是 .
18.一个三角形的三边长的比为3:4:5,且其周长为60cm,则其面积为 .
三、解答题
19.(10分)如图,AC与BD相较于点O,且AB∥CD,点O是AC的中点.试说明:BO=DO.
20.(10分)如图,AB=AD,AC=AE,∠BAE=∠DAC.试说明:∠C=∠E.
21.(10分)如图,点E在AB上,EC是∠BED的角平分线,∠CEB=∠B,∠DCA=∠BCE.试说明:CD=CA.
22.(12分)如图,已知△ABC中,AB=AC,∠C=30°,AB⊥AD.
(1)求∠BDA的度数;
(2)若AD=2,求BC的长.
23.(12分)如图,四边形ABCD中,AB=3cm,BC=4cm,CD=12cm,DA=13cm,且∠ABC=90°.求四边形ABCD的面积.
24.(12分)如图,在△ABC中,AB=AC,点O为∠BAC的平分线上一点,连接OB、OC.
(1)试说明:OB=OC;
(2)若OA=OC,∠BAC=46°,求∠OCB的度数.
25.(12分)如图,△ABC为任意三角形,以AB、AC为边分别向外做等边△ABD和等边△ACE,连接CD、BE并相交于点P.试说明:
(1)CD=BE;
(2)∠BPC=120°.
七年级数学(上)期中试题参考答案
一、选择题
1-5 BBCCC 6-10 BCACC 11-12 DB
二、填空题
13.4 14.45 15.15 16. 或
17.110° 18. 150cm2
解答题
19.解:∵AB∥CD,
∴∠A=∠C,∠B=∠D.
∵点O是AC的中点,
∴AO=CO.
在△ABO和△CDO中,,
∴△ABO≌△CDO(AAS),
∴BO=DO.
20.解:∵∠BAE=∠DAC
∴∠BAE+∠CAE=∠DAC+∠CAE
∴∠CAB=∠EAD,且AB=AD,AC=AE
∴△ABC≌△ADE(SAS)
∴∠C=∠E
21.解:∵∠CEB=∠B,
∴CE=CB.
∵EC平分∠BED,
∴∠CED=∠CEB,
∴∠CED=∠B.
∵∠DCA=∠BCE,
∴∠DCE=∠ACB.
在△DCE和△ACB中,
∴△DCE≌△ACB(ASA).
∴CD=CA.
22.解:(1)∵AB=AC
∴∠B=∠C=30°
∵AD⊥AB
∴∠BDA+∠B=90°
∴∠BDA=60°
(2)∵∠BDA=60°,∠C=30°,且∠BDA=∠C+∠DAC
∴∠DAC=60°﹣30°=30°=∠C
∴AD=CD=2
∵AB⊥AD,∠B=30°
∴BD=2AD=4
∵BC=BD+CD
∴BC=2+4=6
23.解:连接AC,
∵∠ABC=90°,AB=4,BC=3,
∴根据勾股定理AC==5(cm),
又∵CD=12cm,AD=13cm,
∴AC2+DC2=52+122=169,
AD2=132=169,
根据勾股定理的逆定理:∠ACD=90°.
∴四边形ABCD的面积=S△ABC+S△ACD=×3×4+×5×12=36(cm2).
24.解:(1)∵OA平分∠BAC,
∴∠BAO=∠CAO=∠BAC.
在△BAO和△CAO中,
,
∴△BAO≌△CAO(SAS)
∴OB=OC.
(2)由(1)得∴∠BAO=∠CAO=∠BAC,OB=OC,
∵OA=OC,
∴OA=OB=OC,
∴∠OAC=∠OCA=∠BAO=∠OBA=23°,
∵∠OCB=∠OAC+∠OCA+∠BAO+∠OBA=2∠BAC=92°.
25.解:(1)∵以AB、AC为边分别向外做等边△ABD和等边△ACE,
∴AD=AB,AE=AC,∠ACE=∠AEC=60°,∠DAB=∠EAC=60°,
∴∠DAB+∠BAC=∠EAC+∠BAC,
∴∠DAC=∠BAE,
在△DAC和△BAE中,
,
∴△DAC≌△BAE(SAS),
∴CD=BE;
(2)∵△DAC≌△BAE,
∴∠BEA=∠ACD,
∴∠BPC=∠ECP+∠PEC
=∠DCA+∠ACE+∠PEC
=∠BEA+∠ACE+∠PEC
=∠ACE+∠AEC
=60°+60°
=120°.
第5题图
第8题图
第4题图图
第14题图
第17题图
第19题图
第20题图
第21题图
第22题图
第23题图
第24题图
第25题图
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
