14.5 等腰三角形的性质(上海市浦东新区)
文档属性
| 名称 | 14.5 等腰三角形的性质(上海市浦东新区) |

|
|
| 格式 | rar | ||
| 文件大小 | 110.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-12-03 00:00:00 | ||
图片预览


文档简介
课件11张PPT。14.5等腰三角形的性质
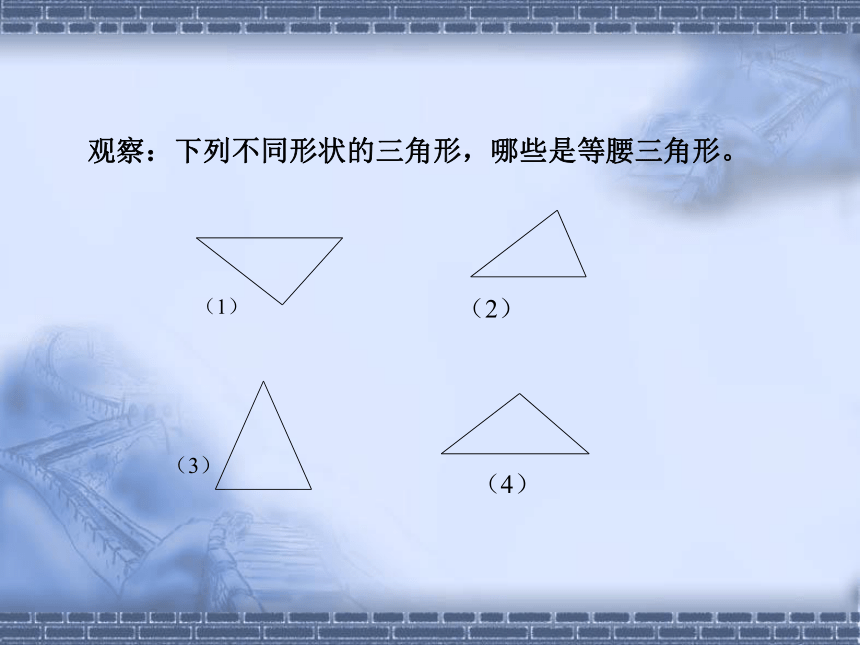
观察:下列不同形状的三角形,哪些是等腰三角形。1.两条边相等的三角形叫等腰三角形;
2.相等的两条边叫做等腰三角形的腰;
3.另一边叫做底边;两腰的夹角叫顶角,
3.腰和底边的夹角叫做底角。ABCDE图中,线段AD叫做三角形
的高;线段BE叫做三角形
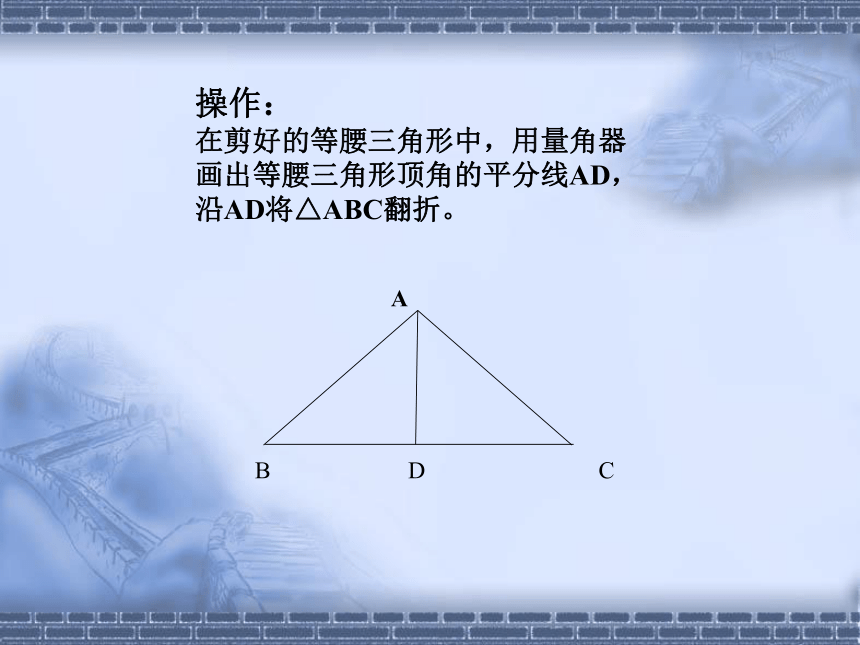
的中线操作:
在剪好的等腰三角形中,用量角器
画出等腰三角形顶角的平分线AD,
沿AD将△ABC翻折。A
B D C
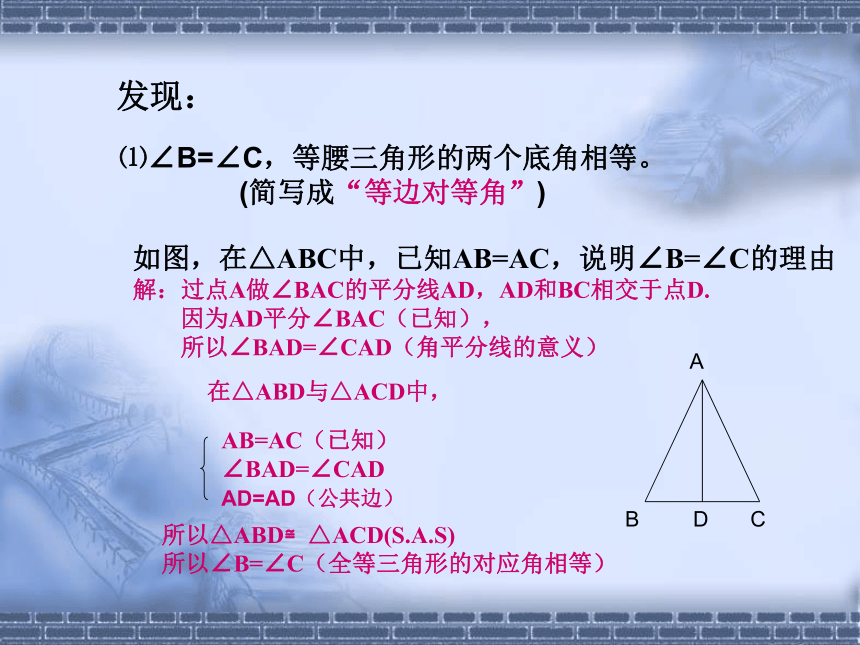
⑴∠B=∠C,等腰三角形的两个底角相等。
(简写成“等边对等角”)发现:如图,在△ABC中,已知AB=AC,说明∠B=∠C的理由
解:过点A做∠BAC的平分线AD,AD和BC相交于点D.
因为AD平分∠BAC(已知),
所以∠BAD=∠CAD(角平分线的意义)在△ABD与△ACD中,AB=AC(已知)
∠BAD=∠CAD
AD=AD(公共边) 所以△ABD≌△ACD(S.A.S)
所以∠B=∠C(全等三角形的对应角相等)AB D C⑵由△ABD≌△ACD,可知BD=CD,
所以AD是底边的中线。
⑶由△ABD≌△ACD,
可知∠ADB=ADC=90o,
所以AD是底边上的高。
即:等腰三角形的顶角平分线、
底边上的中线、底边上的高互相重合,
简称“等腰三角形的三线合一”。 ⑷等腰三角形是轴对称图形,
顶角平分线所在的直线为对称轴。思考:
⑴结合图形,将“等腰三角形的三线合一”的性质
用符号语言表示;
⑵任意一个等腰三角形的底角平分线、
腰上的中线和高,是否重合?例1:已知在△ABC中,AB=AC,∠B=70o,
求∠C和∠A的度数。
解:∵AB=AC(已知),
∴∠C=∠B(等边对等角).
∵∠B=70o(已知),
∴∠C=70o(等量代换).
∴∠A=180o-∠B-∠C=180o-70o-70o=40o
(三角形内角和180o). 例2:等腰三角形一个角是70o,求其余的两个角。 解:⑴当顶角为70o时,
底角=(180o-70o)÷2=55o⑵当底角为70o时,则另一个底角也为70o
顶角=180o-2×70o=40o
所以,其余两角为55o、55o或70o、40o。问题拓展:把例2中的70o改为100o,
会得出什么样的结论?⑴求∠1、∠2的度数;
⑵BD与CD相等吗?为什么?
AD垂直与BC吗?为什么?
解:⑴∵AD平分∠BAC(已知),
∴∠1=∠2(角平分线的意义).
∵∠BAC=110o(已知),
∴∠1=∠2=1/2∠BAC=1/2×110o=55o(等式性质).
⑵∵AB=AC, AD平分∠BAC(已知),
∴BD=DC(等腰三角形顶角平分线与底边上的中线互相重合).
∴AD⊥BC(等腰三角形顶角平分线与底边上的高互相重合). 例3:已知,AB=AC,∠BAC=110o,AD平∠BAC。ABCD三、巩固练习
书107页1、2、3
四、课堂小结
本节课的知识点及收获。
五、作业布置
练习部分55页习题
观察:下列不同形状的三角形,哪些是等腰三角形。1.两条边相等的三角形叫等腰三角形;
2.相等的两条边叫做等腰三角形的腰;
3.另一边叫做底边;两腰的夹角叫顶角,
3.腰和底边的夹角叫做底角。ABCDE图中,线段AD叫做三角形
的高;线段BE叫做三角形
的中线操作:
在剪好的等腰三角形中,用量角器
画出等腰三角形顶角的平分线AD,
沿AD将△ABC翻折。A
B D C
⑴∠B=∠C,等腰三角形的两个底角相等。
(简写成“等边对等角”)发现:如图,在△ABC中,已知AB=AC,说明∠B=∠C的理由
解:过点A做∠BAC的平分线AD,AD和BC相交于点D.
因为AD平分∠BAC(已知),
所以∠BAD=∠CAD(角平分线的意义)在△ABD与△ACD中,AB=AC(已知)
∠BAD=∠CAD
AD=AD(公共边) 所以△ABD≌△ACD(S.A.S)
所以∠B=∠C(全等三角形的对应角相等)AB D C⑵由△ABD≌△ACD,可知BD=CD,
所以AD是底边的中线。
⑶由△ABD≌△ACD,
可知∠ADB=ADC=90o,
所以AD是底边上的高。
即:等腰三角形的顶角平分线、
底边上的中线、底边上的高互相重合,
简称“等腰三角形的三线合一”。 ⑷等腰三角形是轴对称图形,
顶角平分线所在的直线为对称轴。思考:
⑴结合图形,将“等腰三角形的三线合一”的性质
用符号语言表示;
⑵任意一个等腰三角形的底角平分线、
腰上的中线和高,是否重合?例1:已知在△ABC中,AB=AC,∠B=70o,
求∠C和∠A的度数。
解:∵AB=AC(已知),
∴∠C=∠B(等边对等角).
∵∠B=70o(已知),
∴∠C=70o(等量代换).
∴∠A=180o-∠B-∠C=180o-70o-70o=40o
(三角形内角和180o). 例2:等腰三角形一个角是70o,求其余的两个角。 解:⑴当顶角为70o时,
底角=(180o-70o)÷2=55o⑵当底角为70o时,则另一个底角也为70o
顶角=180o-2×70o=40o
所以,其余两角为55o、55o或70o、40o。问题拓展:把例2中的70o改为100o,
会得出什么样的结论?⑴求∠1、∠2的度数;
⑵BD与CD相等吗?为什么?
AD垂直与BC吗?为什么?
解:⑴∵AD平分∠BAC(已知),
∴∠1=∠2(角平分线的意义).
∵∠BAC=110o(已知),
∴∠1=∠2=1/2∠BAC=1/2×110o=55o(等式性质).
⑵∵AB=AC, AD平分∠BAC(已知),
∴BD=DC(等腰三角形顶角平分线与底边上的中线互相重合).
∴AD⊥BC(等腰三角形顶角平分线与底边上的高互相重合). 例3:已知,AB=AC,∠BAC=110o,AD平∠BAC。ABCD三、巩固练习
书107页1、2、3
四、课堂小结
本节课的知识点及收获。
五、作业布置
练习部分55页习题
