7.2.2 用坐标表示平移 教学课件(共27张PPT) 2022—2023学年人教版数学七年级下册
文档属性
| 名称 | 7.2.2 用坐标表示平移 教学课件(共27张PPT) 2022—2023学年人教版数学七年级下册 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-14 00:00:00 | ||
图片预览







文档简介
(共27张PPT)
用坐标表示平移
1、什么叫做平移?
把一个图形整体沿某一方向移动一定的距离,图形的这种移动,叫做平移。
2、平移后得到的新图形与原图形有什么关系?
平移后图形的位置改变,形状、大小不变。
课堂探究
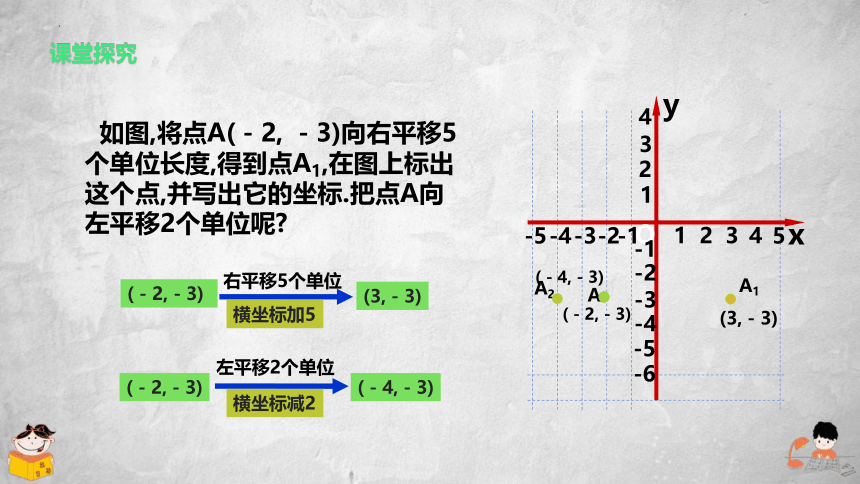
如图,将点A(-2, -3)向右平移5个单位长度,得到点A1,在图上标出这个点,并写出它的坐标.把点A向左平移2个单位呢
x
y
O
1
2
3
4
2
4
1
3
-1
-2
-3
-4
-5
-1
-2
-3
-4
-5
5
-6
A1
(3,-3)
A
(-2,-3)
A2
(-4,-3)
(-2,-3)
右平移5个单位
(3,-3)
横坐标加5
(-2,-3)
左平移2个单位
(-4,-3)
横坐标减2
课堂探究
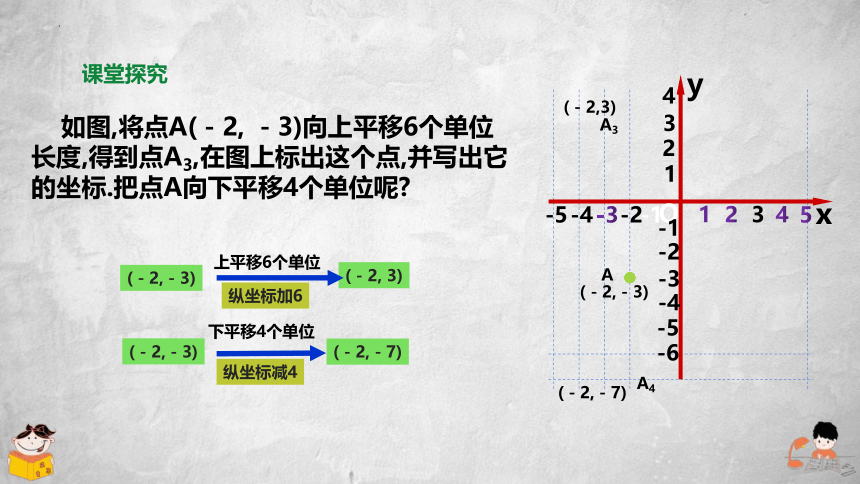
如图,将点A(-2, -3)向上平移6个单位长度,得到点A3,在图上标出这个点,并写出它的坐标.把点A向下平移4个单位呢
x
y
O
1
2
3
4
2
4
1
3
-1
-2
-3
-4
-5
-1
-2
-3
-4
-5
5
-6
A
(-2,-3)
A3
(-2,3)
A4
(-2,-7)
(-2,-3)
上平移6个单位
(-2, 3)
纵坐标加6
(-2,-3)
下平移4个单位
(-2,-7)
纵坐标减4
课堂探究
(1)左、右平移:
向右平移a个单位
(2)上、下平移:
点(x,y)
向左平移a个单位
点(x,y)
(x+a,y)
(x-a,y)
向上平移b个单位
点(x,y)
向下平移b个单位
点(x,y)
(x,y+b)
(x,y-b)
总结规律:点的平移与点的坐标变化间的关系
口 诀
上下平移
左右平移
上加下减横不变
左减右加纵不变
课堂探究
1.在平面直角坐标系中,有一点P(-3,5),若将点P:
(1)向左平移3个单位长度,所得点的坐标为__________;
(2)向右平移5个单位长度,所得点的坐标为___________;
(3)向下平移3个单位长度,所得点的坐标为___________;
(4)向上平移4个单位长度,所得点的坐标为____________;
(-6,5)
(2,5)
(-3, 2)
(-3,9)
练一练
练一练
1、点C1 (x+3,y)可以看作将点C(x,y)向 平移 个单位得到的。
2、点C2 (x-5,y)可以看作将点C(x,y)向 平移 个单位得到的。
3、点D1 (x,y+6)可以看作将点D(x,y)向 平移 个单位得到的。
4、点D2 (x,y-4)可以看作将点D(x,y)向 平移 个单位得到的。
左
3
左
5
上
6
下
逆向说理:
4
如图,正方形ABCD四个顶点的坐标分别是A(-2,4),B(-2,3),C(-1,3),D(-1,4),将正方形ABCD向下平移7个单位长度,再向右平移8个单位长度,两次平移后四个顶点相应变为点E,F,G,H.
(1)点E,F,G,H的坐标分别是什么?如果我们直接平移正方形ABCD,使点A移到点E,它和我们前面得到的正方形位置相同吗?
”
课堂探究
总结:一般地,将一个图形依次沿两个坐标轴方向平移所得到的图形,可以通过将原来的图形作一次平移得到.
解:点E,F,G,H的坐标分别是:(6,-3),(6,-4),(7,-4),(7,-3).
经过平移,可以得出直接平移正方形ABCD,使点A移到点E,同样可以得出上面平移的位置。
课堂探究
例、如图,△ABC三个顶点的坐标 A(4,3),B(3,1),C(1,2)
(1)将三角形ABC三个顶点的
横坐标都减去6,纵坐标不变
(2)依次连接A1,B1,C1,各
点,得到三角形A1B1C1
猜想: △ A1B1C1与△ABC的大小、 形状和位置上有什么关系,为什么?
则有A1 , B1 , C1 。
(-2,3)
(-3,1)
(-5,2)
-3 -2 -1 1 2 3 4 x
3
2
1
-2
-1
-3
4
y
A
B
C
-5
-4
A1
B1
C1
(4,3)
(1,2)
(3,1)
(-2,3)
(-3,1)
(-5,2)
△ A1B1C1与△ABC的大小、 形状完全相同, △ A1B1C1 可以看作将△ABC向左平移6个单位得到。
例题讲解
将△ABC三个顶点的纵坐标都减去5,横坐标不变。
2
3
A2
C2
B2
1
A
C
B
A
C
B
4
x
-
3
y
1
-
1
-
2
-
4
1
2
-
1
-
2
-
3
-
4
0
猜想: △ A2B2C2与△ ABC的大小、形状和位置上有什么关系?
A(4,3) B(3,1) C(1,2)
A2(4,-2)
B2(3,-4)
C2(1,-3)
△ A2B2C2与△ ABC的大小、形状完全相同,△ A2B2C2 可以看作将△ABC向下平移5个单位得到。
课堂探究
思考:将△ABC三个顶点的横坐标都加3,纵坐标不变,纵坐标都加2,横坐标不变,会有怎样的变化?
(1)如图,△A2B2C2 是△ABC向右平移得到的。
A
C
B
A2
C2
B2
A3
C3
B3
(2)如图,△A3B3C3 是△ABC向上平移得到的。
课堂探究
图形向上(或下)平移b个单位长度,也就是将图形上的点(x,y)向上(或下)平移b个单位长度,可以得到对应点(x,y+b)(或(x,y-b))。
总结:在平面直角坐标系中:(图形的平移找特殊点)
图形向右(或左)平移a个单位长度,也就是将图形上的点(x,y)向右(或左)平移a个单位长度,可以得到对应点 (x+a,y)(或(x-a,y));
课堂探究
(3)将△ABC三个顶点的坐标都减 6,纵坐标减5,得到的坐标是多少?
①
②
2
1
-1
-2
-3
-4
-6
-4
-2
2
4
x
y
1
2
3
4
-
2
1
2
-
1
-
5
-
3
-
1
-
2
0
-
3
-
4
-
4
A
C
B
A
C
B
A
C
B
A
1
C
1
B
1
A
1
C
1
B
1
A
1
C
1
B
1
A
3
C
3
B
3
A
1
C
1
B
1
A
1
C
1
B
1
1
2
3
A3(-2,-2)
B3(-3,-4)
C3(-5,-3)
猜想: △ A3B3C3与△ ABC的大小、形状和位置上有什么关系?
△ A2B2C2与△ ABC的大小、形状完全相同,△ A3B3C3 可以看作将△ABC先向左平移6个单位,再向下平移5个单位得到。
课堂探究
归纳总结
向下平移b个单位( )
上、下、左、右平移:
向右平移a个单位
原图形上的点(x,y),
向左平移a个单位
x+a, y+b
x-a, y-b
向上平移b个单位( )
原图形上的点(x,y) ,
例、将点A(1,m)向右平移2个单位长度后,再向上平移1个单位长度得到点Q(n,3),m,n的值分别为多少?
解:由题意得:1+2=n,m+1=3
解得:n=3,m=2.
例题讲解
例题讲解
已知线段MN=4,MN//x轴,若点M坐标为(-1,2),则N点坐标是多少?
解:由题意设点N(-1,y),
∵已知线段MN=4,M坐标为(-1,2),
∴y-2=4,或y-2=-4,
解得y=6或y=-2,
即点N坐标(-1,-2),(-1,6).
1.将点P(m+2,2m+4)向右平移1个单位长度得到点P′,且P′在y轴上,那么P′的坐标是( )
A.(-2,0) B.(0,-2)
C.(1,0) D.(0,1)
2.在平面直角坐标系中,将点(2,3)向上平移1个单位,所得到的点的坐标是( )
A.(1,3) B.(2,2)
C.(2,4) D.(3,3)
B
C
牛刀小试
3.如图,将三角形PQR向右平移2个单位长度,再向下平移3个单位长度,则顶点P平移后的坐标是( )
A.(-2,-4) B.(-2,4)
C.(2,-3) D.(-1,-3)
A
4.在平面直角坐标系中,已知点O(0,0),A(1,3),将线段OA向右平移3个单位,得到线段O1A1,则点O1的坐标是 ,A1的坐标是 .
5.已知△ABC,A(-3,2),B(1,1),C(-1,-2),现将△ABC平移,使点A到点(1,2)的位置上,则点B,C的坐标分别为 , .
(4,3)
(3,0)
(5,-3)
(3,-6)
牛刀小试
6.如图所示,一小船,将其向左平移6个单位长度,再向下平移5个单位长度,试确定A,B,C,D,E,F,G平移后对应点的坐标并画出平移后的图形.
牛刀小试
解:由A(1,2),B(3,1),C(4,1),D(5,2),E(3,2),
F(3,4),G(2,3)可得平移后对应点为:
A′(-5,-3),B′(-3,-4),C′(-2,-4),D′(-1,-3),E′(-3,-3),F′(-3,-1),G′(-4,-2).
平移后的图形如图所示.
牛刀小试
1.如图,三角形ABC内任意一点P(x0,y0),将三角形ABC平移后,点P的对应点为P1(x0+5,y0-3).
(1)写出将三角形ABC平移后,三角形ABC中A,B,C分别对应的点A1,B1,C1的坐标,并画出三角形A1B1C1;
(2)若三角形ABC外有一点M经过同样的平移后得到点M1(5,3),写出M点的坐标 ,若连接线段MM1,PP1,则这两条线段之间的关系是 .
(0,6)
平行且相等
牛刀小试
牛刀小试
2.如图,在平面直角坐标系xOy中,对正方形ABCD及其内部的每个点进行如下操作:把每个点的横、纵坐标都乘以同一实数a,将得到的点先向右平移m个单位,再向上平移n个单位(m>0,n>0),得到正方形A′B′C′D′及其内部的点,其中点A,B的对应点分别为A′,B′.已知正方形ABCD内部的一个点F经过上述操作后得到的对应点F′与点F重合,求点F的坐标.
解:易知AB=6,A′B′=3,
∴a=.
由(-3)×+m=-1,得
m=.
由0×+n=2,得n=2.
设F(x,y),变换后F′(ax+m,ay+n).
∵F与F′重合,
∴ax+m=x,ay+n=y.
∴x+=x,y+2=y.
解得x=1,y=4.∴点F的坐标为(1,4).
牛刀小试
课堂总结
1.平移变换坐标的特点:
x轴(横坐标):向右平移(x+a,y);向左平移(x-a,y)
y轴(纵坐标):向上平移(x,y+a);向下平移(x,y-a)
口诀:右加左减,上加下减
2.平移只改变物体的位置,大小和形状不变,所以图形的平移找特殊点
感谢聆听
用坐标表示平移
1、什么叫做平移?
把一个图形整体沿某一方向移动一定的距离,图形的这种移动,叫做平移。
2、平移后得到的新图形与原图形有什么关系?
平移后图形的位置改变,形状、大小不变。
课堂探究
如图,将点A(-2, -3)向右平移5个单位长度,得到点A1,在图上标出这个点,并写出它的坐标.把点A向左平移2个单位呢
x
y
O
1
2
3
4
2
4
1
3
-1
-2
-3
-4
-5
-1
-2
-3
-4
-5
5
-6
A1
(3,-3)
A
(-2,-3)
A2
(-4,-3)
(-2,-3)
右平移5个单位
(3,-3)
横坐标加5
(-2,-3)
左平移2个单位
(-4,-3)
横坐标减2
课堂探究
如图,将点A(-2, -3)向上平移6个单位长度,得到点A3,在图上标出这个点,并写出它的坐标.把点A向下平移4个单位呢
x
y
O
1
2
3
4
2
4
1
3
-1
-2
-3
-4
-5
-1
-2
-3
-4
-5
5
-6
A
(-2,-3)
A3
(-2,3)
A4
(-2,-7)
(-2,-3)
上平移6个单位
(-2, 3)
纵坐标加6
(-2,-3)
下平移4个单位
(-2,-7)
纵坐标减4
课堂探究
(1)左、右平移:
向右平移a个单位
(2)上、下平移:
点(x,y)
向左平移a个单位
点(x,y)
(x+a,y)
(x-a,y)
向上平移b个单位
点(x,y)
向下平移b个单位
点(x,y)
(x,y+b)
(x,y-b)
总结规律:点的平移与点的坐标变化间的关系
口 诀
上下平移
左右平移
上加下减横不变
左减右加纵不变
课堂探究
1.在平面直角坐标系中,有一点P(-3,5),若将点P:
(1)向左平移3个单位长度,所得点的坐标为__________;
(2)向右平移5个单位长度,所得点的坐标为___________;
(3)向下平移3个单位长度,所得点的坐标为___________;
(4)向上平移4个单位长度,所得点的坐标为____________;
(-6,5)
(2,5)
(-3, 2)
(-3,9)
练一练
练一练
1、点C1 (x+3,y)可以看作将点C(x,y)向 平移 个单位得到的。
2、点C2 (x-5,y)可以看作将点C(x,y)向 平移 个单位得到的。
3、点D1 (x,y+6)可以看作将点D(x,y)向 平移 个单位得到的。
4、点D2 (x,y-4)可以看作将点D(x,y)向 平移 个单位得到的。
左
3
左
5
上
6
下
逆向说理:
4
如图,正方形ABCD四个顶点的坐标分别是A(-2,4),B(-2,3),C(-1,3),D(-1,4),将正方形ABCD向下平移7个单位长度,再向右平移8个单位长度,两次平移后四个顶点相应变为点E,F,G,H.
(1)点E,F,G,H的坐标分别是什么?如果我们直接平移正方形ABCD,使点A移到点E,它和我们前面得到的正方形位置相同吗?
”
课堂探究
总结:一般地,将一个图形依次沿两个坐标轴方向平移所得到的图形,可以通过将原来的图形作一次平移得到.
解:点E,F,G,H的坐标分别是:(6,-3),(6,-4),(7,-4),(7,-3).
经过平移,可以得出直接平移正方形ABCD,使点A移到点E,同样可以得出上面平移的位置。
课堂探究
例、如图,△ABC三个顶点的坐标 A(4,3),B(3,1),C(1,2)
(1)将三角形ABC三个顶点的
横坐标都减去6,纵坐标不变
(2)依次连接A1,B1,C1,各
点,得到三角形A1B1C1
猜想: △ A1B1C1与△ABC的大小、 形状和位置上有什么关系,为什么?
则有A1 , B1 , C1 。
(-2,3)
(-3,1)
(-5,2)
-3 -2 -1 1 2 3 4 x
3
2
1
-2
-1
-3
4
y
A
B
C
-5
-4
A1
B1
C1
(4,3)
(1,2)
(3,1)
(-2,3)
(-3,1)
(-5,2)
△ A1B1C1与△ABC的大小、 形状完全相同, △ A1B1C1 可以看作将△ABC向左平移6个单位得到。
例题讲解
将△ABC三个顶点的纵坐标都减去5,横坐标不变。
2
3
A2
C2
B2
1
A
C
B
A
C
B
4
x
-
3
y
1
-
1
-
2
-
4
1
2
-
1
-
2
-
3
-
4
0
猜想: △ A2B2C2与△ ABC的大小、形状和位置上有什么关系?
A(4,3) B(3,1) C(1,2)
A2(4,-2)
B2(3,-4)
C2(1,-3)
△ A2B2C2与△ ABC的大小、形状完全相同,△ A2B2C2 可以看作将△ABC向下平移5个单位得到。
课堂探究
思考:将△ABC三个顶点的横坐标都加3,纵坐标不变,纵坐标都加2,横坐标不变,会有怎样的变化?
(1)如图,△A2B2C2 是△ABC向右平移得到的。
A
C
B
A2
C2
B2
A3
C3
B3
(2)如图,△A3B3C3 是△ABC向上平移得到的。
课堂探究
图形向上(或下)平移b个单位长度,也就是将图形上的点(x,y)向上(或下)平移b个单位长度,可以得到对应点(x,y+b)(或(x,y-b))。
总结:在平面直角坐标系中:(图形的平移找特殊点)
图形向右(或左)平移a个单位长度,也就是将图形上的点(x,y)向右(或左)平移a个单位长度,可以得到对应点 (x+a,y)(或(x-a,y));
课堂探究
(3)将△ABC三个顶点的坐标都减 6,纵坐标减5,得到的坐标是多少?
①
②
2
1
-1
-2
-3
-4
-6
-4
-2
2
4
x
y
1
2
3
4
-
2
1
2
-
1
-
5
-
3
-
1
-
2
0
-
3
-
4
-
4
A
C
B
A
C
B
A
C
B
A
1
C
1
B
1
A
1
C
1
B
1
A
1
C
1
B
1
A
3
C
3
B
3
A
1
C
1
B
1
A
1
C
1
B
1
1
2
3
A3(-2,-2)
B3(-3,-4)
C3(-5,-3)
猜想: △ A3B3C3与△ ABC的大小、形状和位置上有什么关系?
△ A2B2C2与△ ABC的大小、形状完全相同,△ A3B3C3 可以看作将△ABC先向左平移6个单位,再向下平移5个单位得到。
课堂探究
归纳总结
向下平移b个单位( )
上、下、左、右平移:
向右平移a个单位
原图形上的点(x,y),
向左平移a个单位
x+a, y+b
x-a, y-b
向上平移b个单位( )
原图形上的点(x,y) ,
例、将点A(1,m)向右平移2个单位长度后,再向上平移1个单位长度得到点Q(n,3),m,n的值分别为多少?
解:由题意得:1+2=n,m+1=3
解得:n=3,m=2.
例题讲解
例题讲解
已知线段MN=4,MN//x轴,若点M坐标为(-1,2),则N点坐标是多少?
解:由题意设点N(-1,y),
∵已知线段MN=4,M坐标为(-1,2),
∴y-2=4,或y-2=-4,
解得y=6或y=-2,
即点N坐标(-1,-2),(-1,6).
1.将点P(m+2,2m+4)向右平移1个单位长度得到点P′,且P′在y轴上,那么P′的坐标是( )
A.(-2,0) B.(0,-2)
C.(1,0) D.(0,1)
2.在平面直角坐标系中,将点(2,3)向上平移1个单位,所得到的点的坐标是( )
A.(1,3) B.(2,2)
C.(2,4) D.(3,3)
B
C
牛刀小试
3.如图,将三角形PQR向右平移2个单位长度,再向下平移3个单位长度,则顶点P平移后的坐标是( )
A.(-2,-4) B.(-2,4)
C.(2,-3) D.(-1,-3)
A
4.在平面直角坐标系中,已知点O(0,0),A(1,3),将线段OA向右平移3个单位,得到线段O1A1,则点O1的坐标是 ,A1的坐标是 .
5.已知△ABC,A(-3,2),B(1,1),C(-1,-2),现将△ABC平移,使点A到点(1,2)的位置上,则点B,C的坐标分别为 , .
(4,3)
(3,0)
(5,-3)
(3,-6)
牛刀小试
6.如图所示,一小船,将其向左平移6个单位长度,再向下平移5个单位长度,试确定A,B,C,D,E,F,G平移后对应点的坐标并画出平移后的图形.
牛刀小试
解:由A(1,2),B(3,1),C(4,1),D(5,2),E(3,2),
F(3,4),G(2,3)可得平移后对应点为:
A′(-5,-3),B′(-3,-4),C′(-2,-4),D′(-1,-3),E′(-3,-3),F′(-3,-1),G′(-4,-2).
平移后的图形如图所示.
牛刀小试
1.如图,三角形ABC内任意一点P(x0,y0),将三角形ABC平移后,点P的对应点为P1(x0+5,y0-3).
(1)写出将三角形ABC平移后,三角形ABC中A,B,C分别对应的点A1,B1,C1的坐标,并画出三角形A1B1C1;
(2)若三角形ABC外有一点M经过同样的平移后得到点M1(5,3),写出M点的坐标 ,若连接线段MM1,PP1,则这两条线段之间的关系是 .
(0,6)
平行且相等
牛刀小试
牛刀小试
2.如图,在平面直角坐标系xOy中,对正方形ABCD及其内部的每个点进行如下操作:把每个点的横、纵坐标都乘以同一实数a,将得到的点先向右平移m个单位,再向上平移n个单位(m>0,n>0),得到正方形A′B′C′D′及其内部的点,其中点A,B的对应点分别为A′,B′.已知正方形ABCD内部的一个点F经过上述操作后得到的对应点F′与点F重合,求点F的坐标.
解:易知AB=6,A′B′=3,
∴a=.
由(-3)×+m=-1,得
m=.
由0×+n=2,得n=2.
设F(x,y),变换后F′(ax+m,ay+n).
∵F与F′重合,
∴ax+m=x,ay+n=y.
∴x+=x,y+2=y.
解得x=1,y=4.∴点F的坐标为(1,4).
牛刀小试
课堂总结
1.平移变换坐标的特点:
x轴(横坐标):向右平移(x+a,y);向左平移(x-a,y)
y轴(纵坐标):向上平移(x,y+a);向下平移(x,y-a)
口诀:右加左减,上加下减
2.平移只改变物体的位置,大小和形状不变,所以图形的平移找特殊点
感谢聆听
