2022--2023学年人教版七年级数学下册9. 2一元一次不等式 同步精练 同步练习(含答案)
文档属性
| 名称 | 2022--2023学年人教版七年级数学下册9. 2一元一次不等式 同步精练 同步练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 389.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-14 19:16:54 | ||
图片预览

文档简介
9.2 一元一次不等式 同步精练
一、单选题
1.不等式3x+2<2x+3的解集在数轴上表示正确的是( )
A. B.C. D.
2.x的与x的和不超过5用不等式可以表示为( )
A.+x≤5 B.+x<5 C.+x≥5 D.+x>5
3.已知的解满足y﹣x<1,则k的取值范围是( )
A.k>1 B.k<﹣ C.k>0 D.k<1
4.已知关于x,y的二元一次方程,当x取不同值时,对应y的值分别如下表所示:
x … -1 0 1 2 3 …
y … 3 2 1 0 -1 …
则关于x的不等式的解集为( )A. B. C. D.
5.不等式2x>4的解有( )
A.1个 B.2个
C.3个 D.无限多个
6.不等式组的解表示在数轴上,正确的是( )
A. B.
C. D.
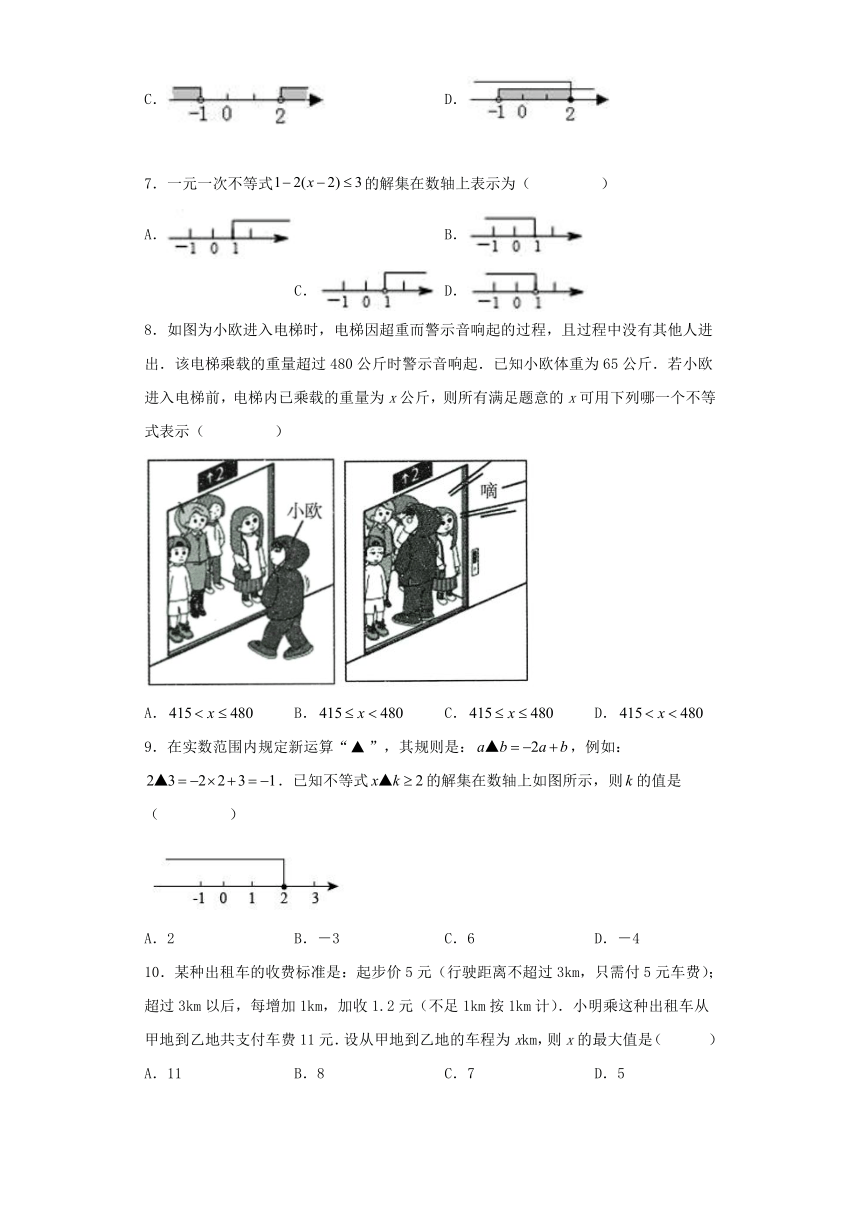
7.一元一次不等式的解集在数轴上表示为( )
A. B. C. D.
8.如图为小欧进入电梯时,电梯因超重而警示音响起的过程,且过程中没有其他人进出.该电梯乘载的重量超过480公斤时警示音响起.已知小欧体重为65公斤.若小欧进入电梯前,电梯内已乘载的重量为x公斤,则所有满足题意的x可用下列哪一个不等式表示( )
A. B. C. D.
9.在实数范围内规定新运算“”,其规则是:,例如:.已知不等式的解集在数轴上如图所示,则的值是( )
A.2 B.-3 C.6 D.-4
10.某种出租车的收费标准是:起步价5元(行驶距离不超过3km,只需付5元车费);超过3km以后,每增加1km,加收1.2元(不足1km按1km计).小明乘这种出租车从甲地到乙地共支付车费11元.设从甲地到乙地的车程为xkm,则x的最大值是( )
A.11 B.8 C.7 D.5
二、填空题
11.解不等式:,其解集为_________________ .
12.满足不等式的正整数是______.
13.关于的不等式的解集为,请写出一组满足条件的实数a,b的值:a=_____ ,b=________.
14.“x不小于2”用不等式可表示为_____________;
15.某超市为了促销一种定价为3元的商品,采取下列方式优惠销售:若一次性购买不超过5件,按原价付款;若一次性购买5件以上,超过部分按原价八折付款.如果小明有30元钱,那么他最多可以购______件.
三、解答题
16.解下列不等式组
(1).
(2)
(3)
17.用适当的符号表示下面的关系:
(1)a的一半比a与3的差小. (2)x的与5的差小于1.
(3)x与6的和大于-7. (4)8与y的2倍的和是正数.
(5)a的3倍与7的差是负数.
18.对于实数 ,我们定义符号的意义为: 当时,; 当时,;如:;,根据该定义运算完成下列问题:
(1)_______,当时,_______;
(2)若 ,求的取值范围;
(3)若关于 的函数为,求该函数的最大值.
19.某地区为绿化环境,计划购买甲、乙两种树苗共计棵.有关甲、乙两种树苗的信息如图所示.
信 息 1.甲种树苗每棵60元; 2.乙种树苗每棵90元; 3.甲种树苗的成活率为; 4.乙种树苗的成活率为.
(1)当时,如果购买甲、乙两种树苗公用27000元,那么甲、乙两种树苗各买了多少棵?
(2)实际购买这两种树苗的总费用恰好为27000元,其中甲种树苗买了棵.
①写出与满足的关系式;
②要使这批树苗的成活率不低于,求的最大值.
20.我们定义一个关于实数m,n的新运算,规定:m※n=4m﹣3n,例如:5※2=4×5﹣3×2=14,若m满足m※2<0,求m的取值范围.
参考答案
1.D
2.A
3.D
4.D
5.D
6.D
7.A
8.A
9.C
10.B
11.x<2
12.1
13. -1(答案不唯一) 0(答案不唯一)
14.x≥2
15.11
16.(1)
(2)
(3)
17.(1) (2) (3) (4) (5)
18.(1),
(2)
(3)2
19.(1)甲种树苗购买了300棵,乙种树苗购买了100棵
(2)①;②375
20.
一、单选题
1.不等式3x+2<2x+3的解集在数轴上表示正确的是( )
A. B.C. D.
2.x的与x的和不超过5用不等式可以表示为( )
A.+x≤5 B.+x<5 C.+x≥5 D.+x>5
3.已知的解满足y﹣x<1,则k的取值范围是( )
A.k>1 B.k<﹣ C.k>0 D.k<1
4.已知关于x,y的二元一次方程,当x取不同值时,对应y的值分别如下表所示:
x … -1 0 1 2 3 …
y … 3 2 1 0 -1 …
则关于x的不等式的解集为( )A. B. C. D.
5.不等式2x>4的解有( )
A.1个 B.2个
C.3个 D.无限多个
6.不等式组的解表示在数轴上,正确的是( )
A. B.
C. D.
7.一元一次不等式的解集在数轴上表示为( )
A. B. C. D.
8.如图为小欧进入电梯时,电梯因超重而警示音响起的过程,且过程中没有其他人进出.该电梯乘载的重量超过480公斤时警示音响起.已知小欧体重为65公斤.若小欧进入电梯前,电梯内已乘载的重量为x公斤,则所有满足题意的x可用下列哪一个不等式表示( )
A. B. C. D.
9.在实数范围内规定新运算“”,其规则是:,例如:.已知不等式的解集在数轴上如图所示,则的值是( )
A.2 B.-3 C.6 D.-4
10.某种出租车的收费标准是:起步价5元(行驶距离不超过3km,只需付5元车费);超过3km以后,每增加1km,加收1.2元(不足1km按1km计).小明乘这种出租车从甲地到乙地共支付车费11元.设从甲地到乙地的车程为xkm,则x的最大值是( )
A.11 B.8 C.7 D.5
二、填空题
11.解不等式:,其解集为_________________ .
12.满足不等式的正整数是______.
13.关于的不等式的解集为,请写出一组满足条件的实数a,b的值:a=_____ ,b=________.
14.“x不小于2”用不等式可表示为_____________;
15.某超市为了促销一种定价为3元的商品,采取下列方式优惠销售:若一次性购买不超过5件,按原价付款;若一次性购买5件以上,超过部分按原价八折付款.如果小明有30元钱,那么他最多可以购______件.
三、解答题
16.解下列不等式组
(1).
(2)
(3)
17.用适当的符号表示下面的关系:
(1)a的一半比a与3的差小. (2)x的与5的差小于1.
(3)x与6的和大于-7. (4)8与y的2倍的和是正数.
(5)a的3倍与7的差是负数.
18.对于实数 ,我们定义符号的意义为: 当时,; 当时,;如:;,根据该定义运算完成下列问题:
(1)_______,当时,_______;
(2)若 ,求的取值范围;
(3)若关于 的函数为,求该函数的最大值.
19.某地区为绿化环境,计划购买甲、乙两种树苗共计棵.有关甲、乙两种树苗的信息如图所示.
信 息 1.甲种树苗每棵60元; 2.乙种树苗每棵90元; 3.甲种树苗的成活率为; 4.乙种树苗的成活率为.
(1)当时,如果购买甲、乙两种树苗公用27000元,那么甲、乙两种树苗各买了多少棵?
(2)实际购买这两种树苗的总费用恰好为27000元,其中甲种树苗买了棵.
①写出与满足的关系式;
②要使这批树苗的成活率不低于,求的最大值.
20.我们定义一个关于实数m,n的新运算,规定:m※n=4m﹣3n,例如:5※2=4×5﹣3×2=14,若m满足m※2<0,求m的取值范围.
参考答案
1.D
2.A
3.D
4.D
5.D
6.D
7.A
8.A
9.C
10.B
11.x<2
12.1
13. -1(答案不唯一) 0(答案不唯一)
14.x≥2
15.11
16.(1)
(2)
(3)
17.(1) (2) (3) (4) (5)
18.(1),
(2)
(3)2
19.(1)甲种树苗购买了300棵,乙种树苗购买了100棵
(2)①;②375
20.
