沪科版七下10.2《平行线的判定(三)》课件
文档属性
| 名称 | 沪科版七下10.2《平行线的判定(三)》课件 |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-05-26 10:34:39 | ||
图片预览




文档简介
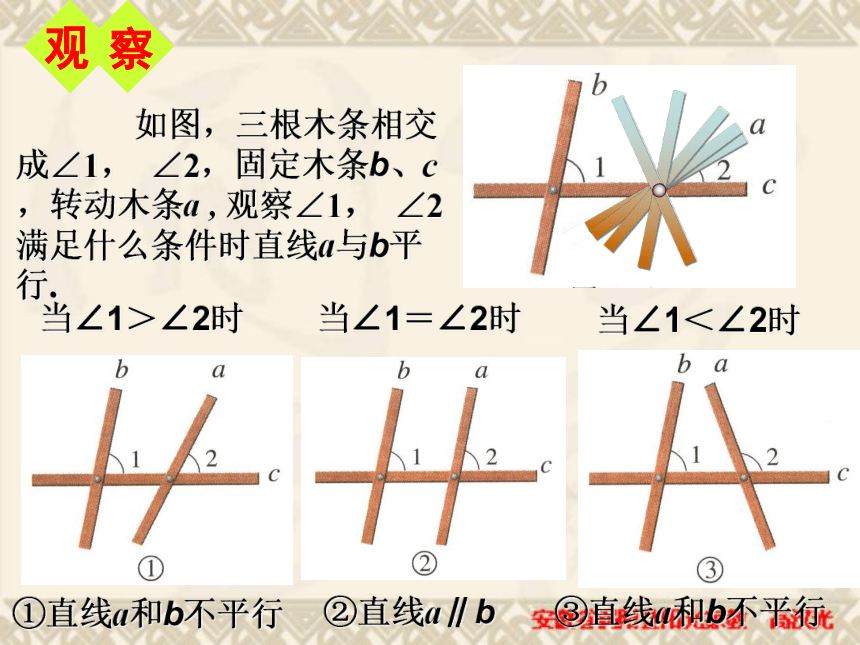
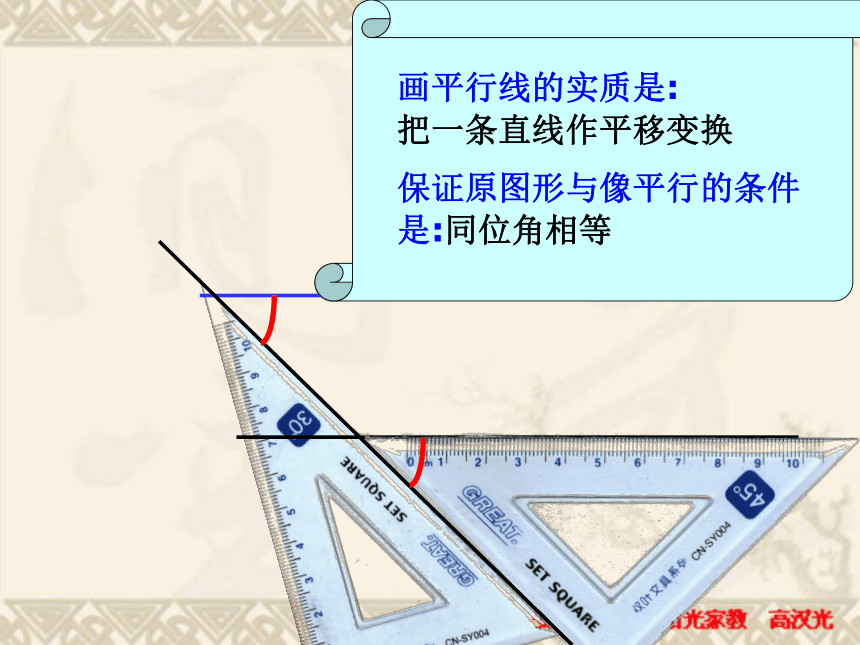
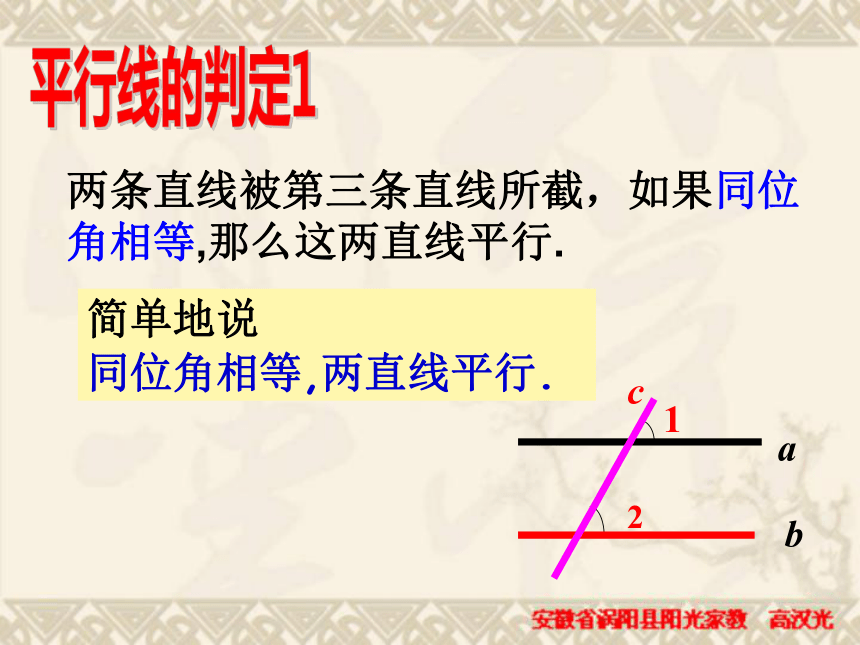
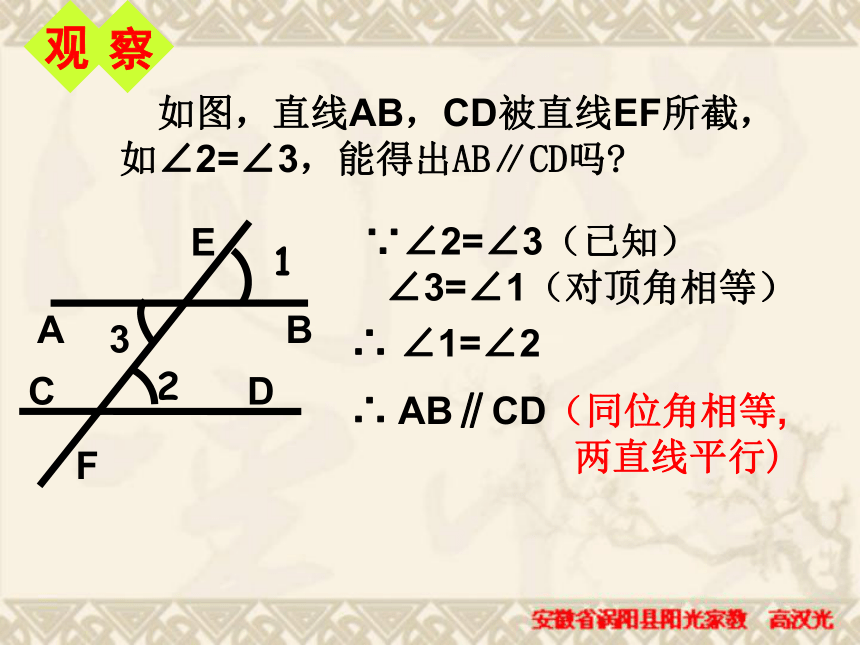
课件27张PPT。10.2平行线的判定(三) 如图,三根木条相交成∠1, ∠2,固定木条b、c,转动木条a , 观察∠1, ∠2满足什么条件时直线a与b平行.当∠1>∠2时当∠1=∠2时当∠1<∠2时①直线a和b不平行②直线a∥b③直线a和b不平行一、放二、靠三、移四、画平行线的画法:“推平行线法”: 平行线的判定1两条直线被第三条直线所截,如果同位角相等,那么这两直线平行.简单地说
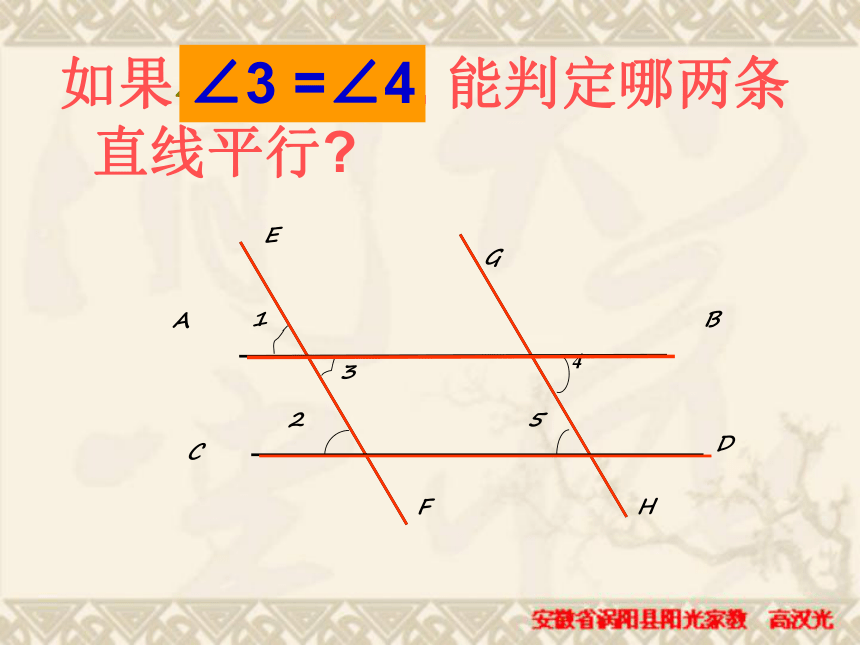
同位角相等,两直线平行.4123ABCEFD5HG∠3 =∠4 如图,直线AB,CD被直线EF所截,如∠2=∠3,能得出AB∥CD吗?∵∠2=∠3(已知)
∠3=∠1(对顶角相等)∴ ∠1=∠2∴ AB∥CD(同位角相等,
两直线平行)两条直线被第三条直线所截,如果内错角相等,那么这两直线平行.∵∠2=∠3(已知)
∴ AB∥CD
(内错角相等,两直线平行)推理格式: 简单地说
内错角相等,两直线平行.平行线的判定2 如图,已知∠1=121°,
∠2 =120°, ∠3=120°.
说出其中的平行线,并说明理由.如图,如果∠3+∠4=180°
那么AB∥CD?∵ ∠3+∠4=180 °(已知)
∠2+∠4=180°(邻补角的定义)∴ ∠3=∠2( )∴ AB∥CD( )32AC1DBEF4同角的补角相等内错角相等, 两直线平行两条直线被第三条直线所截,如果同旁内角互补,那么这两直线平行.推理格式:∵ ∠2+∠3=180 °(已知)
∴ AB∥CD
(同旁内角互补, 两直线平行)
简单地说
同旁内角互补,两直线平行平行线的判定3例1① ∵ ∠2 =___(已知)
∴ ___∥___( )② ∵ ∠3 = ∠5(已知)
∴ ___∥___( )③∵ ∠4 +___=180o(已知)
∴ ___∥___( )∠6ABCDABCD∠5ABCDAC14235867BD同位角相等,两直线平行内错角相等,两直线平行同旁内角互补,两直线平行例2① ∵ ∠1 =_____(已知)
∴ AB∥CE( )② ∵ ∠1 +_____=180o(已知)
∴ CD∥BF( )③ ∵ ∠1 +∠5 =180o(已知)
∴ _____∥_____( )ABCE∠2④ ∵ ∠4 +_____=180o(已知)
∴ CE∥AB( )∠3∠313542CFEADB内错角相等,两直线平行同旁内角互补,两直线平行同旁内角互补,两直线平行同旁内角互补,两直线平行例3如图,已知 ∠1=75o , ∠2 =105o
问:AB与CD平行吗?为什么?AC1423BD5已知∠3=45 °,∠1与∠2互余,试说明 ? 解:由于∠1与∠2是对顶角,
∴∠1=∠2
又∵∠1+∠2=90°(已知)
∴∠1=∠2=45°
∵ ∠3=45°(已知)
∴∠ 2=∠3
∴ AB∥CD(内错角相等,两直线平行)AB//CD
(1)从∠1=∠2,可以推出 ∥ ,
理由是 。
(2)从∠2=∠ ,可以推出c∥d ,
理由是 。
(3)如果∠1=75°,∠4=105°,
可以推出 ∥ 。
理由是 。练一练ba内错角相等,两直线平行同位角相等,两直线平行3cd42cd31ab同旁内角互补,两直线平行1.如图从∠1=∠4,可以推出 ∥ ,
理由是 。(3)从∠ABC +∠ =180,可以推出AB∥CD ,
理由是 。(2)从∠ =∠ ,可以推出AD∥BC,
理由是 。(4)从∠5=∠ ,可以推出AB∥CD,
理由是 。练一练AB内错角相等,两直线平行CDBCD同旁内角互补,两直线平行23内错角相等,两直线平行ABC同位角相等,两直线平行2.如图3.两条直线垂直于同一条直线,这两条
直线平行吗?为什么?答:垂直于同一条直线的两条直线平行.练一练因为 b⊥a所以 ∠2=90° (垂直的定义)从而b∥c. (同位角相等,两直线平行)所以 ∠1=90° (垂直的定义)因为 c ⊥a所以 ∠1=∠2(等量代换)解法1:理由:如图,
∵ b⊥a,c⊥a(已知)
∴∠1=∠2=90°(垂直定义)
∴b∥c(内错角相等,两直线平行)abc12解法2:理由:如图,
∵ b⊥a,c⊥a(已知)
∴∠1=∠2=90°(垂直定义)
∴ ∠1+∠2=180°
∴b∥c(同旁内角互补,两直线平行)abc12解法3:结论如果两条直线都垂直于同一条直线,
那么这两条直线平行。bca有一块木板,身边只有直尺和量角器,我们怎样才能知道它上下边缘是否平行?试一试12方案1:45° 45° 45°1245°方案2:135° 45°方案3:理一理同位角相等
内错角相等
同旁内角互补平行条件4. 在同一平面内,垂直于同一条直线的两直线平行
5.平行线的定义.
1.在同一个平面内,不相交的两条直线。
2.如果两条直线都与第三条直线平行,
那么这两条直线也互相平行.
3.同位角相等, 两直线平行.
4.内错角相等, 两直线平行.
5.同旁内角互补, 两直线平行.
6.如果两条直线都与第三条直线垂直,
那么这两条直线也互相平行.
判定两条直线是否平行的方法有:讲一讲
同位角相等,两直线平行.4123ABCEFD5HG∠3 =∠4 如图,直线AB,CD被直线EF所截,如∠2=∠3,能得出AB∥CD吗?∵∠2=∠3(已知)
∠3=∠1(对顶角相等)∴ ∠1=∠2∴ AB∥CD(同位角相等,
两直线平行)两条直线被第三条直线所截,如果内错角相等,那么这两直线平行.∵∠2=∠3(已知)
∴ AB∥CD
(内错角相等,两直线平行)推理格式: 简单地说
内错角相等,两直线平行.平行线的判定2 如图,已知∠1=121°,
∠2 =120°, ∠3=120°.
说出其中的平行线,并说明理由.如图,如果∠3+∠4=180°
那么AB∥CD?∵ ∠3+∠4=180 °(已知)
∠2+∠4=180°(邻补角的定义)∴ ∠3=∠2( )∴ AB∥CD( )32AC1DBEF4同角的补角相等内错角相等, 两直线平行两条直线被第三条直线所截,如果同旁内角互补,那么这两直线平行.推理格式:∵ ∠2+∠3=180 °(已知)
∴ AB∥CD
(同旁内角互补, 两直线平行)
简单地说
同旁内角互补,两直线平行平行线的判定3例1① ∵ ∠2 =___(已知)
∴ ___∥___( )② ∵ ∠3 = ∠5(已知)
∴ ___∥___( )③∵ ∠4 +___=180o(已知)
∴ ___∥___( )∠6ABCDABCD∠5ABCDAC14235867BD同位角相等,两直线平行内错角相等,两直线平行同旁内角互补,两直线平行例2① ∵ ∠1 =_____(已知)
∴ AB∥CE( )② ∵ ∠1 +_____=180o(已知)
∴ CD∥BF( )③ ∵ ∠1 +∠5 =180o(已知)
∴ _____∥_____( )ABCE∠2④ ∵ ∠4 +_____=180o(已知)
∴ CE∥AB( )∠3∠313542CFEADB内错角相等,两直线平行同旁内角互补,两直线平行同旁内角互补,两直线平行同旁内角互补,两直线平行例3如图,已知 ∠1=75o , ∠2 =105o
问:AB与CD平行吗?为什么?AC1423BD5已知∠3=45 °,∠1与∠2互余,试说明 ? 解:由于∠1与∠2是对顶角,
∴∠1=∠2
又∵∠1+∠2=90°(已知)
∴∠1=∠2=45°
∵ ∠3=45°(已知)
∴∠ 2=∠3
∴ AB∥CD(内错角相等,两直线平行)AB//CD
(1)从∠1=∠2,可以推出 ∥ ,
理由是 。
(2)从∠2=∠ ,可以推出c∥d ,
理由是 。
(3)如果∠1=75°,∠4=105°,
可以推出 ∥ 。
理由是 。练一练ba内错角相等,两直线平行同位角相等,两直线平行3cd42cd31ab同旁内角互补,两直线平行1.如图从∠1=∠4,可以推出 ∥ ,
理由是 。(3)从∠ABC +∠ =180,可以推出AB∥CD ,
理由是 。(2)从∠ =∠ ,可以推出AD∥BC,
理由是 。(4)从∠5=∠ ,可以推出AB∥CD,
理由是 。练一练AB内错角相等,两直线平行CDBCD同旁内角互补,两直线平行23内错角相等,两直线平行ABC同位角相等,两直线平行2.如图3.两条直线垂直于同一条直线,这两条
直线平行吗?为什么?答:垂直于同一条直线的两条直线平行.练一练因为 b⊥a所以 ∠2=90° (垂直的定义)从而b∥c. (同位角相等,两直线平行)所以 ∠1=90° (垂直的定义)因为 c ⊥a所以 ∠1=∠2(等量代换)解法1:理由:如图,
∵ b⊥a,c⊥a(已知)
∴∠1=∠2=90°(垂直定义)
∴b∥c(内错角相等,两直线平行)abc12解法2:理由:如图,
∵ b⊥a,c⊥a(已知)
∴∠1=∠2=90°(垂直定义)
∴ ∠1+∠2=180°
∴b∥c(同旁内角互补,两直线平行)abc12解法3:结论如果两条直线都垂直于同一条直线,
那么这两条直线平行。bca有一块木板,身边只有直尺和量角器,我们怎样才能知道它上下边缘是否平行?试一试12方案1:45° 45° 45°1245°方案2:135° 45°方案3:理一理同位角相等
内错角相等
同旁内角互补平行条件4. 在同一平面内,垂直于同一条直线的两直线平行
5.平行线的定义.
1.在同一个平面内,不相交的两条直线。
2.如果两条直线都与第三条直线平行,
那么这两条直线也互相平行.
3.同位角相等, 两直线平行.
4.内错角相等, 两直线平行.
5.同旁内角互补, 两直线平行.
6.如果两条直线都与第三条直线垂直,
那么这两条直线也互相平行.
判定两条直线是否平行的方法有:讲一讲
