10.1探究杠杆的平衡条件(共37张PPT)-沪科版物理八年级下
文档属性
| 名称 | 10.1探究杠杆的平衡条件(共37张PPT)-沪科版物理八年级下 |  | |
| 格式 | zip | ||
| 文件大小 | 9.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-04-13 23:46:57 | ||
图片预览







文档简介
(共37张PPT)
第五节 探究杠杆的平衡条件
在生活、 生产中,人们常常用撬棒撬物、用起重机吊物等,这其中有什么奥秘 让我们从跷跷板开始进行探究。
探究跷跷板中的道理
小时候,我们都玩过跷跷板。观察如图6- 37所示的情景后, 讨论一下,大人和小朋友分别坐在跷跷板的两侧,怎样才能使跷跷板保持水平呢
为了便于探究跷跷板怎样才能保持水平 白 白状态,需要对它简化进行实验研究。如图6-38所示,用带有等分刻度的均质木尺代替跷跷板,用钩码代替人。
物理学中,把能绕某. 固定点转动的硬棒(直棒或曲棒),叫做杠杆(lever)。跷跷板是一种杠杆。
活动1 探究杠杆的平衡条件
首先调节杠杆两端的螺母,使杠杆处于水平平衡状态。接着在杠杆的两边分别挂上数量不同的钩码,用F、F2表示钩码的拉力,用L、L2表示钩码离开悬挂点0的距离(图6-39)。改变钩码数量和它们离开点0的距离,使杠杆处于水平静止状态。将各次实验所得的数据填入下表中。
杠杆绕着转动的点
(图6- 40中的点0),叫
做支点(fulcrum)。
从支点到力作用线
的距离L和L叫做力臂
(force arm)。动力的
力臂叫做动力臂,阻力
的力臂叫做阻力臂。
杠杆在动力和阻力
作用下处于静止状态,
叫做杠杆平衡( balance )。
请运用上述概念,分析实验中的数据,用文字和公式归纳结论。
(1) 提出问题:
杠杆平衡时,动力、动力臂、阻力、阻力臂之间存在着怎样的关系?
(2)猜想与假设:
假设1:
假设2:
假设3:
假设4:
F1+L1=F2+L2
F1–L1=F2–L2
F1/L1=F2/L2
F1 · L1=F2 · L2
2. 杠杆的平衡条件
还有其他假设吗?
F12+L12=F22+L22
F13+L13=F23+L23
……
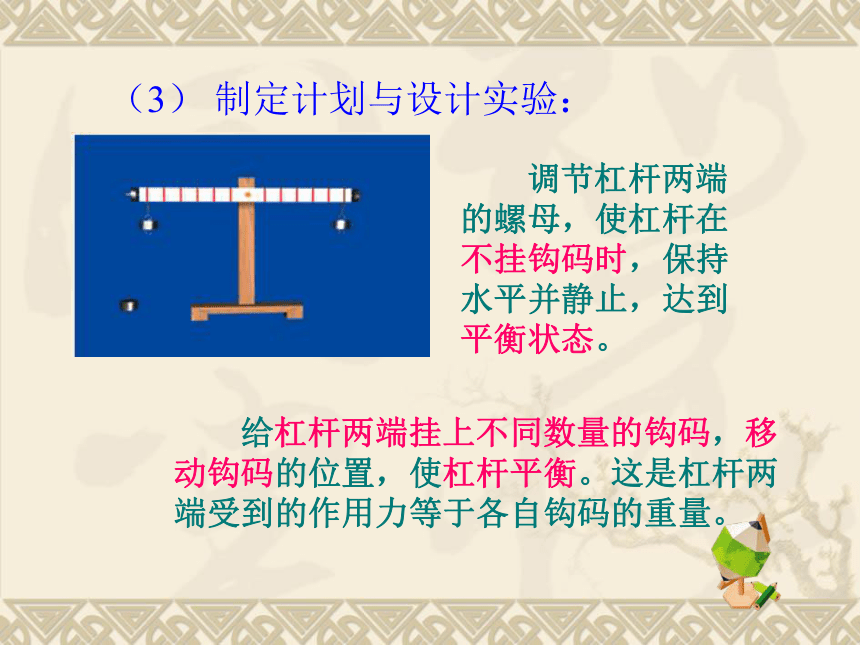
调节杠杆两端的螺母,使杠杆在不挂钩码时,保持水平并静止,达到平衡状态。
给杠杆两端挂上不同数量的钩码,移动钩码的位置,使杠杆平衡。这是杠杆两端受到的作用力等于各自钩码的重量。
(3) 制定计划与设计实验:
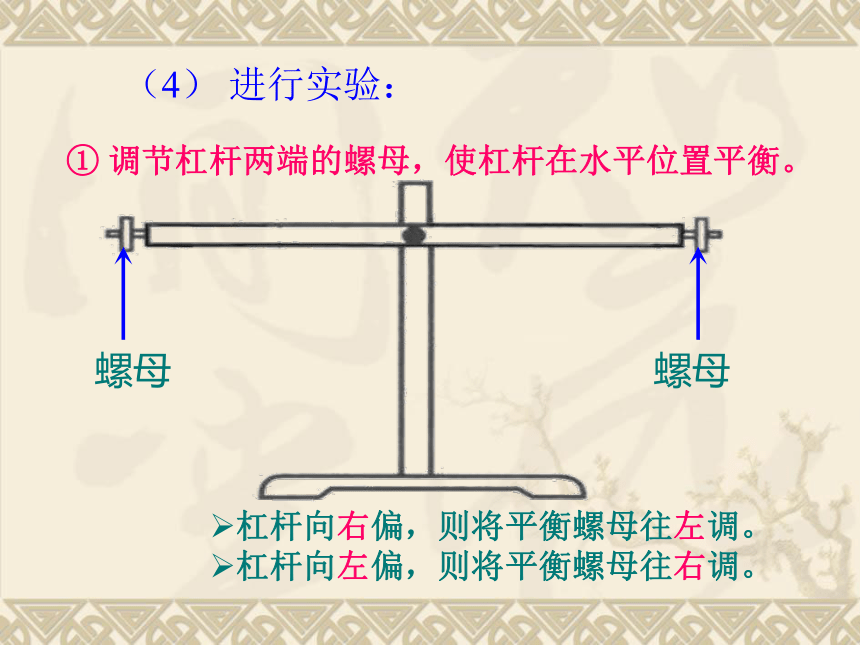
① 调节杠杆两端的螺母,使杠杆在水平位置平衡。
螺母
螺母
(4) 进行实验:
杠杆向右偏,则将平衡螺母往左调。
杠杆向左偏,则将平衡螺母往右调。
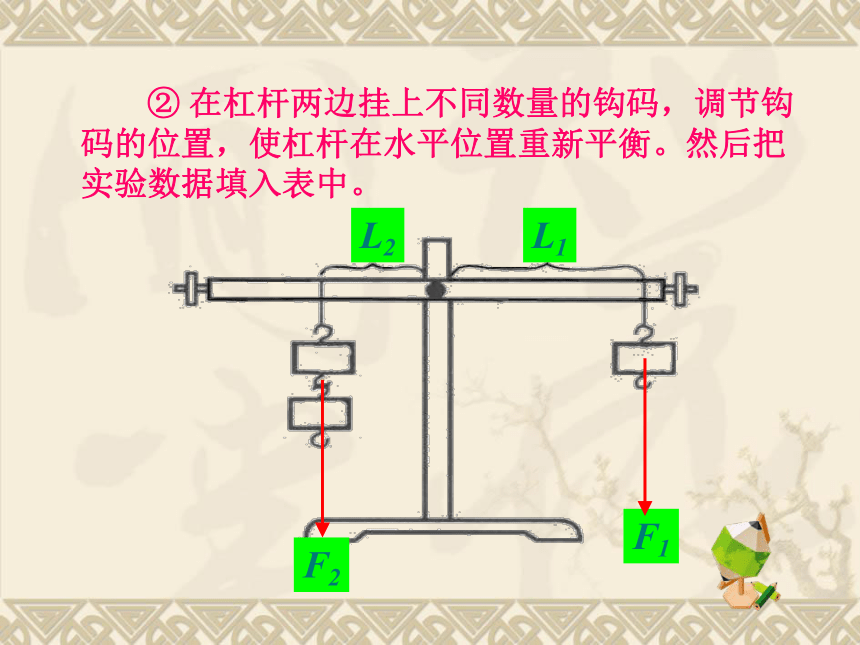
② 在杠杆两边挂上不同数量的钩码,调节钩码的位置,使杠杆在水平位置重新平衡。然后把实验数据填入表中。
F2
F1
L2
L1
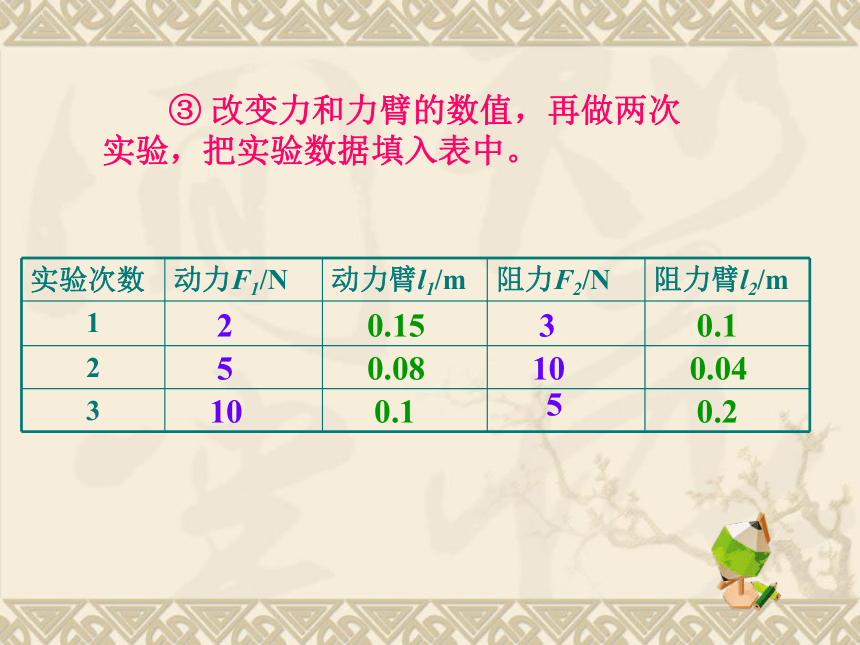
③ 改变力和力臂的数值,再做两次实验,把实验数据填入表中。
实验次数 动力F1/N 动力臂l1/m 阻力F2/N 阻力臂l2/m
1
2
3
2
0.15
3
0.1
5
0.08
10
0.04
10
0.1
5
0.2
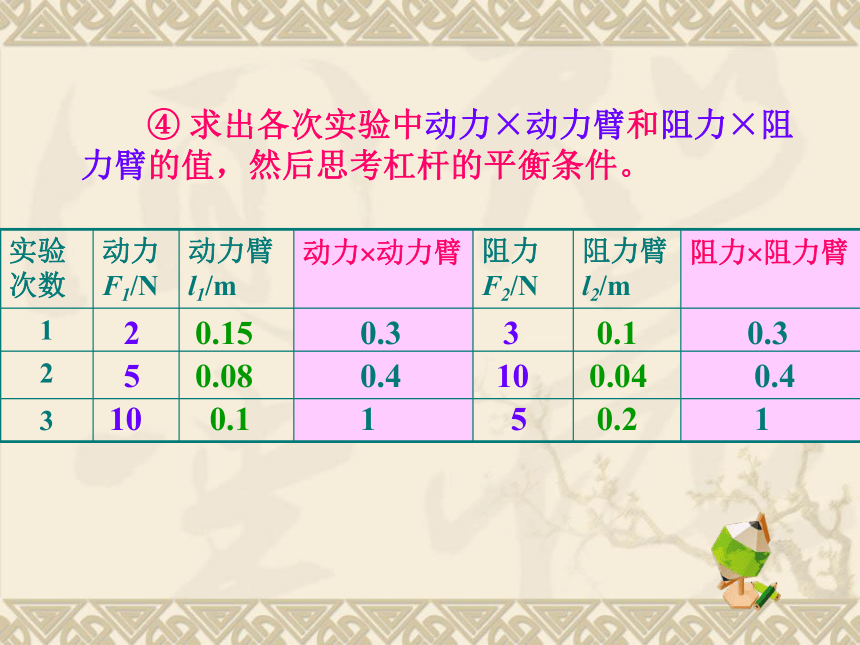
④ 求出各次实验中动力×动力臂和阻力×阻力臂的值,然后思考杠杆的平衡条件。
实验次数 动力F1/N 动力臂l1/m 动力 动力臂 阻力F2/N 阻力臂l2/m 阻力 阻力臂
1
2
3
2
0.15
3
0.1
5
0.08
10
0.04
10
0.1
5
0.2
0.3
0.3
0.4
0.4
1
1
杠杆的平衡条件是:
(5) 得出结论:
动力×动力臂=阻力×阻力臂
或写作: F1L1= F2L2
即:杠杆的平衡取决于力和力臂的乘积。
阿基米德杠杆原理
上面的关系也可以写成下面的形式:
阻力 动力臂
动力 阻力臂
或
F1 L2
F2 L1
动力 阻力臂
阻力 动力臂
或
F1 L2
F2 L1
杠杆两端可调节的平衡螺母,起什么作用
为什么要求杠杆静止时,在水平位置
平衡螺母调节杠杆自身的平衡。
力臂的数值在杠杆上可以直接读出或量出。
(6)交流与合作:
挂钩码后,能不能再调节平衡螺母?
不能。
上式表明,杠杆平衡时,杠杆的动力乘动力臂等于阻力乘阻力臂,即杠杆的动力臂是阻力臂的几倍,杠杆的动力F就是阻力F2的几分之一。这就是杠杆的平衡条件。
例题假如图6- 37中的大人重750N,小女孩重250N。当大人坐在与跷跷板的转轴距离为0.5 m处,小女孩应该坐在哪里才能使跷跷板水平平衡
已知:阻力F,=750N,阻力臂L=0.5m,动力F=250N。
求:动力臂L的大小。
解:根据杠杆平衡条件F1L1=F2L2,得
答:小女孩应该坐在离转轴1.5 m处。
讨论:
1.根据杠杆平衡条件,比较动力臂和阻力臂的长短,怎样的杠杆省力 怎样的杠杆费力 怎样的杠杆既不省力又不费力
2.比较图6-41中三种剪刀的动力臂、阻力臂长短有什么不同 请说明其中的道理。
杠杆的作用
活动2 认识生活中的杠杆
生活和生产中有许多不同形式的杠杆。
请画出图6-42中各种器具的支点和力臂。画力臂时要注意,它应该是支点到力的作用线的距离。
讨论:上图中哪些杠杆省力,哪些杠杆费力,哪些杠杆既不省力也不费力 使用这三类杠杆各有什么好处
3. 杠杆的应用
(1)根据杠杆平衡条件: F1×L1=F2×L2
若L1>L2,则 F1省力杠杆特点:省力但要费距离。
手通过的距离比刀口通过的距离大,要多移动距离。
省力杠杆
铡刀
省力杠杆
道钉撬
羊角锤
起子
钳子
手动抽水机
(2)根据杠杆平衡条件: F1×L1=F2×L2
若L1F2。此杠杆为费力杠杆。
费力杠杆特点:费力但可以省距离。
手通过的距离比煤或鱼通过的距离少得多,可以省距离。
铁锹
钓鱼竿
费力杠杆
费力杠杆
缝纫机脚踏板
起重机
剪刀
镊子
人的胳膊
筷子
(3)根据杠杆平衡条件: F1×L1=F2×L2
若L1=L2,则 F1=F2。此杠杆为等臂杠杆。
等臂杠杆特点:不省力也不省距离。
阻力臂L2
动力臂L1
O
动力臂L1
阻力臂L2
F1
F2
人体内许多部位的骨骼和肌肉组织也构成杠杆。如图6- 43所示,手上握着或托着重物时,可将手、手腕、尺骨和桡骨看作一一个整体,它的作用相当于杠杆(肘关节相当于支点)。
机械手操作时,模仿手的动作,同样具有杠杆的特征(图6- 44)。
信息浏览
传说, 阿基米德(Archimedes,前287- 前212) 发现了杠杆原理后,曾产生撬动地球的遐想。他在给叙拉古国国王希罗的信中写道:“只要给我一个支点和一根足够长的杠杆,我就能撬动地球。”国王看信后,立即召见了阿基米德,并说:“当着众神发誓,你真的能撬动地球吗 ”阿基米德不慌不忙地用撬石头的例子作比喻,向国王讲了杠杆的原理,然后坦然回答说:“不,我只是根据原理作了这样的推理。事实上,我站不
到地球以外的什么地方去,找不到这样长而坚固的杠杆,也找不到搁这根杠杆的支点。”国王弄懂了这个道理,很高兴。
4. 杠杆的种类:
省力杠杆:L1>L2,动力小于阻力
特点:省力,但费距离。应用:羊角锤
费力杠杆:L1 特点:费力,但省距离。应用:钓鱼竿
等臂杠杆:L1=L2 ,动力等于阻力
特点:不省力也不费力。应用:天平
3. 杠杆的平衡条件:
动力×动力臂=阻力×阻力臂
F1L1= F2L2
小结
自我评价与作业
1.你是否动手做过“探究杠杆的平衡条件”的实验 如果没有,请在家中做一下。
2.画出图6-46中各力的力臂。
3.工人用一辆独轮车
搬运泥土。设车斗和泥土
的总重力G=1000N,独轮
车各部分如图6-47所示,
那么,工人运泥土时抬起
独轮车需要用的力F是多少
4.一位体重约为500N的同学在做俯卧撑,如图6-48所示,点A为重心。请计算地面对他双手的作用力。
5.图6-49是拉杆式旅行箱的受力示意图。若箱重100N,动力臂是阻力臂的4倍,则拉箱子时,竖直向上的拉力F=____N。
巩固练习
1. 力臂是一定在杠杆上吗?
答:不是。
F1
F2
L1
L2
3. 若力作用在杠杆上,作用点不变,但作用方向改变,力臂是否改变?
答:改变。
F1
O
L1
L2
F2
4. 哪种剪纸方法省力? 哪种剪纸方法省距离?
1. 蹬自行车脚踏板时,如果只向下用力,则当脚踏板在水平位置时,动力臂最大,这时用力效果最好。
2. 剪较硬的物体阻力较大,要用动力臂比阻力臂长的剪刀。
剪纸或布时,阻力不很大,用动力臂较短的剪刀,完成一次剪裁动作,可以剪裁较长的纸或布,加快剪切速度。修剪树枝时,一方面树枝较硬、阻力较大,这就要求动力臂要长,阻力臂要短;另一方面,为了加快修剪速度,剪切整齐,要求剪刀刀口要长,就要用动力臂较长、阻力臂较短,同时刀口较长的剪刀。
4. 指甲剪上有三个杠杆。手把部分是一个省力杠杆,刀口部分是两个费力杠杆。
用剪刀剪物体时,被剪物体的具体位置不同,阻力臂的大小也不同,动力的大小也会变化。不能说动力一定大于或一定小于阻力,一般是根据轴到手柄的距离来粗略地判断某种剪刀是不是省力杠杆。手柄长的剪刀能省力,通常用来剪坚硬的物体,手柄短的剪刀费力,通常用来剪轻软物体。
第五节 探究杠杆的平衡条件
在生活、 生产中,人们常常用撬棒撬物、用起重机吊物等,这其中有什么奥秘 让我们从跷跷板开始进行探究。
探究跷跷板中的道理
小时候,我们都玩过跷跷板。观察如图6- 37所示的情景后, 讨论一下,大人和小朋友分别坐在跷跷板的两侧,怎样才能使跷跷板保持水平呢
为了便于探究跷跷板怎样才能保持水平 白 白状态,需要对它简化进行实验研究。如图6-38所示,用带有等分刻度的均质木尺代替跷跷板,用钩码代替人。
物理学中,把能绕某. 固定点转动的硬棒(直棒或曲棒),叫做杠杆(lever)。跷跷板是一种杠杆。
活动1 探究杠杆的平衡条件
首先调节杠杆两端的螺母,使杠杆处于水平平衡状态。接着在杠杆的两边分别挂上数量不同的钩码,用F、F2表示钩码的拉力,用L、L2表示钩码离开悬挂点0的距离(图6-39)。改变钩码数量和它们离开点0的距离,使杠杆处于水平静止状态。将各次实验所得的数据填入下表中。
杠杆绕着转动的点
(图6- 40中的点0),叫
做支点(fulcrum)。
从支点到力作用线
的距离L和L叫做力臂
(force arm)。动力的
力臂叫做动力臂,阻力
的力臂叫做阻力臂。
杠杆在动力和阻力
作用下处于静止状态,
叫做杠杆平衡( balance )。
请运用上述概念,分析实验中的数据,用文字和公式归纳结论。
(1) 提出问题:
杠杆平衡时,动力、动力臂、阻力、阻力臂之间存在着怎样的关系?
(2)猜想与假设:
假设1:
假设2:
假设3:
假设4:
F1+L1=F2+L2
F1–L1=F2–L2
F1/L1=F2/L2
F1 · L1=F2 · L2
2. 杠杆的平衡条件
还有其他假设吗?
F12+L12=F22+L22
F13+L13=F23+L23
……
调节杠杆两端的螺母,使杠杆在不挂钩码时,保持水平并静止,达到平衡状态。
给杠杆两端挂上不同数量的钩码,移动钩码的位置,使杠杆平衡。这是杠杆两端受到的作用力等于各自钩码的重量。
(3) 制定计划与设计实验:
① 调节杠杆两端的螺母,使杠杆在水平位置平衡。
螺母
螺母
(4) 进行实验:
杠杆向右偏,则将平衡螺母往左调。
杠杆向左偏,则将平衡螺母往右调。
② 在杠杆两边挂上不同数量的钩码,调节钩码的位置,使杠杆在水平位置重新平衡。然后把实验数据填入表中。
F2
F1
L2
L1
③ 改变力和力臂的数值,再做两次实验,把实验数据填入表中。
实验次数 动力F1/N 动力臂l1/m 阻力F2/N 阻力臂l2/m
1
2
3
2
0.15
3
0.1
5
0.08
10
0.04
10
0.1
5
0.2
④ 求出各次实验中动力×动力臂和阻力×阻力臂的值,然后思考杠杆的平衡条件。
实验次数 动力F1/N 动力臂l1/m 动力 动力臂 阻力F2/N 阻力臂l2/m 阻力 阻力臂
1
2
3
2
0.15
3
0.1
5
0.08
10
0.04
10
0.1
5
0.2
0.3
0.3
0.4
0.4
1
1
杠杆的平衡条件是:
(5) 得出结论:
动力×动力臂=阻力×阻力臂
或写作: F1L1= F2L2
即:杠杆的平衡取决于力和力臂的乘积。
阿基米德杠杆原理
上面的关系也可以写成下面的形式:
阻力 动力臂
动力 阻力臂
或
F1 L2
F2 L1
动力 阻力臂
阻力 动力臂
或
F1 L2
F2 L1
杠杆两端可调节的平衡螺母,起什么作用
为什么要求杠杆静止时,在水平位置
平衡螺母调节杠杆自身的平衡。
力臂的数值在杠杆上可以直接读出或量出。
(6)交流与合作:
挂钩码后,能不能再调节平衡螺母?
不能。
上式表明,杠杆平衡时,杠杆的动力乘动力臂等于阻力乘阻力臂,即杠杆的动力臂是阻力臂的几倍,杠杆的动力F就是阻力F2的几分之一。这就是杠杆的平衡条件。
例题假如图6- 37中的大人重750N,小女孩重250N。当大人坐在与跷跷板的转轴距离为0.5 m处,小女孩应该坐在哪里才能使跷跷板水平平衡
已知:阻力F,=750N,阻力臂L=0.5m,动力F=250N。
求:动力臂L的大小。
解:根据杠杆平衡条件F1L1=F2L2,得
答:小女孩应该坐在离转轴1.5 m处。
讨论:
1.根据杠杆平衡条件,比较动力臂和阻力臂的长短,怎样的杠杆省力 怎样的杠杆费力 怎样的杠杆既不省力又不费力
2.比较图6-41中三种剪刀的动力臂、阻力臂长短有什么不同 请说明其中的道理。
杠杆的作用
活动2 认识生活中的杠杆
生活和生产中有许多不同形式的杠杆。
请画出图6-42中各种器具的支点和力臂。画力臂时要注意,它应该是支点到力的作用线的距离。
讨论:上图中哪些杠杆省力,哪些杠杆费力,哪些杠杆既不省力也不费力 使用这三类杠杆各有什么好处
3. 杠杆的应用
(1)根据杠杆平衡条件: F1×L1=F2×L2
若L1>L2,则 F1
手通过的距离比刀口通过的距离大,要多移动距离。
省力杠杆
铡刀
省力杠杆
道钉撬
羊角锤
起子
钳子
手动抽水机
(2)根据杠杆平衡条件: F1×L1=F2×L2
若L1
费力杠杆特点:费力但可以省距离。
手通过的距离比煤或鱼通过的距离少得多,可以省距离。
铁锹
钓鱼竿
费力杠杆
费力杠杆
缝纫机脚踏板
起重机
剪刀
镊子
人的胳膊
筷子
(3)根据杠杆平衡条件: F1×L1=F2×L2
若L1=L2,则 F1=F2。此杠杆为等臂杠杆。
等臂杠杆特点:不省力也不省距离。
阻力臂L2
动力臂L1
O
动力臂L1
阻力臂L2
F1
F2
人体内许多部位的骨骼和肌肉组织也构成杠杆。如图6- 43所示,手上握着或托着重物时,可将手、手腕、尺骨和桡骨看作一一个整体,它的作用相当于杠杆(肘关节相当于支点)。
机械手操作时,模仿手的动作,同样具有杠杆的特征(图6- 44)。
信息浏览
传说, 阿基米德(Archimedes,前287- 前212) 发现了杠杆原理后,曾产生撬动地球的遐想。他在给叙拉古国国王希罗的信中写道:“只要给我一个支点和一根足够长的杠杆,我就能撬动地球。”国王看信后,立即召见了阿基米德,并说:“当着众神发誓,你真的能撬动地球吗 ”阿基米德不慌不忙地用撬石头的例子作比喻,向国王讲了杠杆的原理,然后坦然回答说:“不,我只是根据原理作了这样的推理。事实上,我站不
到地球以外的什么地方去,找不到这样长而坚固的杠杆,也找不到搁这根杠杆的支点。”国王弄懂了这个道理,很高兴。
4. 杠杆的种类:
省力杠杆:L1>L2,动力小于阻力
特点:省力,但费距离。应用:羊角锤
费力杠杆:L1
等臂杠杆:L1=L2 ,动力等于阻力
特点:不省力也不费力。应用:天平
3. 杠杆的平衡条件:
动力×动力臂=阻力×阻力臂
F1L1= F2L2
小结
自我评价与作业
1.你是否动手做过“探究杠杆的平衡条件”的实验 如果没有,请在家中做一下。
2.画出图6-46中各力的力臂。
3.工人用一辆独轮车
搬运泥土。设车斗和泥土
的总重力G=1000N,独轮
车各部分如图6-47所示,
那么,工人运泥土时抬起
独轮车需要用的力F是多少
4.一位体重约为500N的同学在做俯卧撑,如图6-48所示,点A为重心。请计算地面对他双手的作用力。
5.图6-49是拉杆式旅行箱的受力示意图。若箱重100N,动力臂是阻力臂的4倍,则拉箱子时,竖直向上的拉力F=____N。
巩固练习
1. 力臂是一定在杠杆上吗?
答:不是。
F1
F2
L1
L2
3. 若力作用在杠杆上,作用点不变,但作用方向改变,力臂是否改变?
答:改变。
F1
O
L1
L2
F2
4. 哪种剪纸方法省力? 哪种剪纸方法省距离?
1. 蹬自行车脚踏板时,如果只向下用力,则当脚踏板在水平位置时,动力臂最大,这时用力效果最好。
2. 剪较硬的物体阻力较大,要用动力臂比阻力臂长的剪刀。
剪纸或布时,阻力不很大,用动力臂较短的剪刀,完成一次剪裁动作,可以剪裁较长的纸或布,加快剪切速度。修剪树枝时,一方面树枝较硬、阻力较大,这就要求动力臂要长,阻力臂要短;另一方面,为了加快修剪速度,剪切整齐,要求剪刀刀口要长,就要用动力臂较长、阻力臂较短,同时刀口较长的剪刀。
4. 指甲剪上有三个杠杆。手把部分是一个省力杠杆,刀口部分是两个费力杠杆。
用剪刀剪物体时,被剪物体的具体位置不同,阻力臂的大小也不同,动力的大小也会变化。不能说动力一定大于或一定小于阻力,一般是根据轴到手柄的距离来粗略地判断某种剪刀是不是省力杠杆。手柄长的剪刀能省力,通常用来剪坚硬的物体,手柄短的剪刀费力,通常用来剪轻软物体。
同课章节目录
- 第一章 打开物理世界的大门
- 第一节 走进神奇
- 第二节 探索之路
- 第三节 站在巨人的肩膀上
- 第二章 运动的世界
- 第一节 动与静
- 第二节 长度与时间的测量
- 第三节 快与慢
- 第四节 科学探究:速度的变化
- 第三章 声的世界
- 第一节 科学探究:声音的产生与传播
- 第二节 声音的特性
- 第三节 超声与次声
- 第四章 多彩的光
- 第一节 光的反射
- 第二节 平面镜成像
- 第三节 光的折射
- 第四节 光的色散
- 第五节 科学探究:凸透镜成像
- 第六节 神奇的眼睛
- 第五章 质量与密度
- 第一节 质量
- 第二节 学习使用天平和量筒
- 第三节 科学探究:物质的密度
- 第四节 密度知识的应用
- 第六章 熟悉而陌生的力
- 第一节 力
- 第二节 怎样描述力
- 第三节 弹力与弹簧测力计
- 第四节 来自地球的力
- 第五节 科学探究:摩擦力
- 第七章 力与运动
- 第一节 科学探究:牛顿第一定律
- 第二节 力的合成
- 第三节 力的平衡
- 第八章 压强
- 第一节 压力的作用效果
- 第二节 科学探究:液体的压强
- 第三节 空气的“力量”
- 第四节 流体压强与流速的关系
- 第九章 浮力
- 第一节 认识浮力
- 第二节 阿基米德原理
- 第三节 物体的浮与沉
- 第十章 机械与人
- 第一节 科学探究:杠杆的平衡条件
- 第二节 滑轮及其应用
- 第三节 做功了吗
- 第四节 做功的快慢
- 第五节 机械效率
- 第六节 合理利用机械能
- 第十一章 小粒子与大宇宙
- 第一节 走进微观
- 第二节 看不见的运动
- 第三节 探索宇宙
