2023年浙江省中考科学复习——物理解答题练习(含答案)
文档属性
| 名称 | 2023年浙江省中考科学复习——物理解答题练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 317.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 科学 | ||
| 更新时间 | 2023-04-14 00:00:00 | ||
图片预览



文档简介
物理解答题
1.如图所示,一个内底面积为100 cm2的柱形容器中盛有深度为60 cm的水,水底有一块底面积为50 cm2,高为6 cm的长方体铝块。现用一电动机以恒定不变的输出功率把铝块提出水面并继续提升一段距离。已知铝块浸没在水中时上升速度恒为0.27 m/s。铝的密度为2.7×103 kg/m3,g取10 N/kg,铝块提升过程中受到的阻力、绳子自重和摩擦等都不计。求:
(1)铝块的重力。
(2)把铝块提升到上表面与水面相平所需的时间。
(3)电动机输出功率的大小。
(4)铝块完全露出水面后匀速上升的速度。
(5)铝块从浸没于水中到完全露出水面,水对容器底部压强的减小值。
2.小雨通过如图甲所示滑轮组将水中物体匀速提升至空中,他所用拉力与绳子自由端移动能距离的关系图象如图乙所示。其中物体在空中匀速上升过程中滑轮组的机械效率为.每个滑轮等重,不计绳重、摩擦和水的阻力。(水的密度为求:
(1)物体在空中上升,小雨做的功是多少?
(2)每个滑轮的重力是多少?
(3)物体的密度是多少?
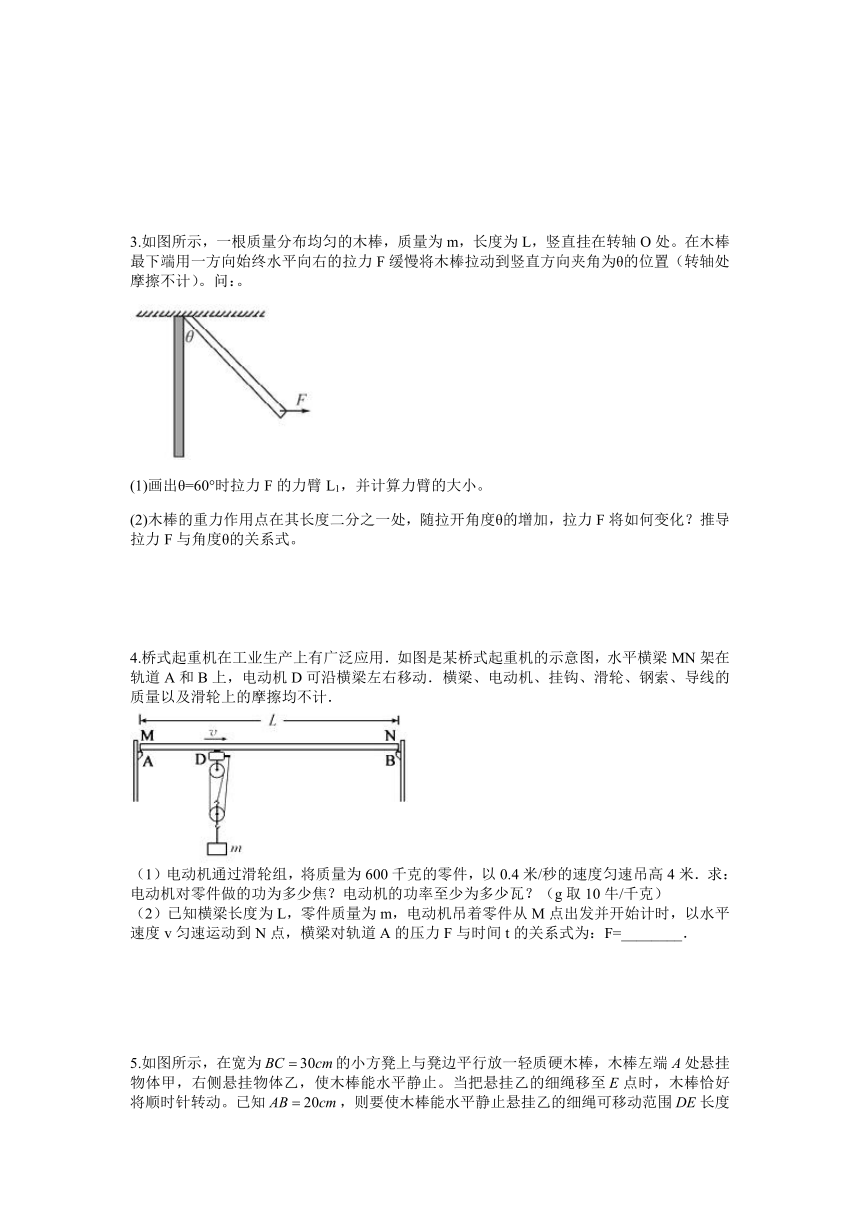
3.如图所示,一根质量分布均匀的木棒,质量为m,长度为L,竖直挂在转轴O处。在木棒最下端用一方向始终水平向右的拉力F缓慢将木棒拉动到竖直方向夹角为θ的位置(转轴处摩擦不计)。问:。
(1)画出θ=60°时拉力F的力臂L1,并计算力臂的大小。
(2)木棒的重力作用点在其长度二分之一处,随拉开角度θ的增加,拉力F将如何变化?推导拉力F与角度θ的关系式。
4.桥式起重机在工业生产上有广泛应用.如图是某桥式起重机的示意图,水平横梁MN架在轨道A和B上,电动机D可沿横梁左右移动.横梁、电动机、挂钩、滑轮、钢索、导线的质量以及滑轮上的摩擦均不计.
(1)电动机通过滑轮组,将质量为600千克的零件,以0.4米/秒的速度匀速吊高4米.求:电动机对零件做的功为多少焦?电动机的功率至少为多少瓦?(g取10牛/千克)
(2)已知横梁长度为L,零件质量为m,电动机吊着零件从M点出发并开始计时,以水平速度v匀速运动到N点,横梁对轨道A的压力F与时间t的关系式为:F=________.
5.如图所示,在宽为的小方凳上与凳边平行放一轻质硬木棒,木棒左端处悬挂物体甲,右侧悬挂物体乙,使木棒能水平静止。当把悬挂乙的细绳移至点时,木棒恰好将顺时针转动。已知,则要使木棒能水平静止悬挂乙的细绳可移动范围长度是多少?
6.实验室里可以用欧姆表来直接测量电阻。如图虚线框内是欧姆表的简化结构图,它由灵敏电流表、电源、变阻器等组成。在a、b间接入一个电阻R,路中就有一个对应电流I,即电阻R与电流表的读数I有一一对应关系。所以,由电流表的指针位置可以知道电阻R大小。为了方便,事先在电流表的刻度盘上标出了电阻的欧姆值。欧姆表在测量电阻前都需要调零,即把a、b两接线柱短接,调节变阻器的滑片位置,使电流表满偏(指在最大刻度处)
(1)普通电流表示数标识情况为左小右大,那么改装后的欧姆表示数的标识情况为________。
(2)若某欧姆表的刻度值是按电源电压为1.5V来刻度的,满偏电流为10mA.那么5mA位置时,对应的电阻值为________Ω.在使用一段时间后,发现电源电压降为1.2V,用这个欧姆表测得某电阻为350Ω,则这个电阻的实际值为(不考虑电源本身的电阻)________Ω。
7.如图甲所示是一种家庭水箱水位测量装置示意图,电源电压18V保持不变,电压表量程0 15V,电流表量程0 3A,R0是阻值为10Ω的定值电阻,R1是长20cm、阻值为20Ω的电阻丝,滑片P把电阻丝与轻质弹簧的指针连在一起。圆柱体M长80cm,底面积为200cm2 . 当水位处于最高处时,M刚好浸没在水中,滑片P恰好在R1的最上端。轻质弹簧阻值不计,M全部露出水面前,弹簧的伸长长度△L始终与受到的拉力F成正比,如图乙所示。
(1)如要求电表指针偏转的幅度随水位的上升而增大,则选用电路中________表的示数来显示水位变化。
(2)当水位处于最高处时,电压表的示数为多少?
(3)当水位下降,圆柱体露出水面部分的长度为50cm时,电流表示数为多少?(g取10N/kg)
8.一根金属棒AB置于水平地面上,今通过弹簧测力计竖直地将棒的右端B缓慢拉起,如图甲所示,在此过程中,弹簧测力计对棒所做的功W与B端离开地面的高度x的关系如图乙所示,请根据图象解答下列问题.
(1)该金属棒的长度l=________m;
(2)在B端拉起的过程中,当x1=0.6m时,测力计的示数为F1=________N;当x2=1.6m时,测力计的示数F2=________N.
(3)求金属棒的重心到A端的距离d.
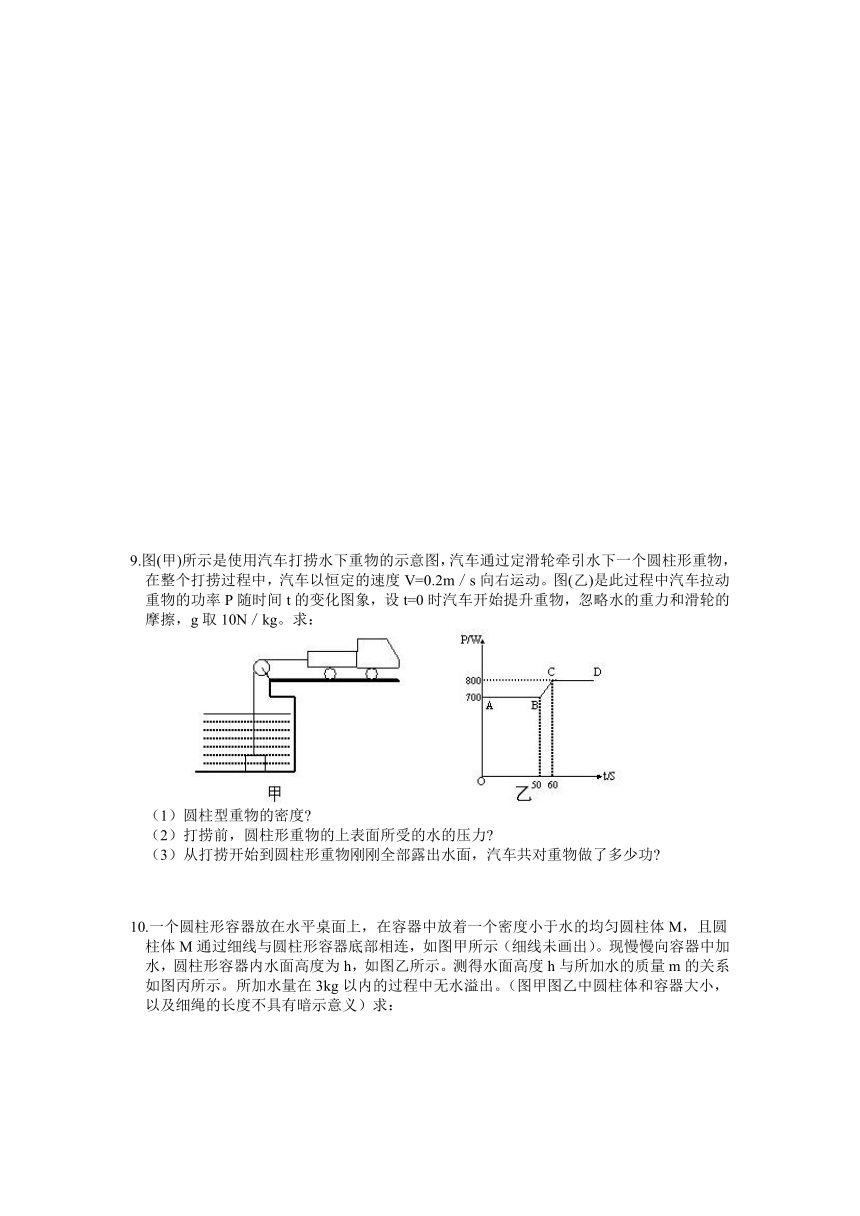
9.图(甲)所示是使用汽车打捞水下重物的示意图,汽车通过定滑轮牵引水下一个圆柱形重物,在整个打捞过程中,汽车以恒定的速度V=0.2m/s向右运动。图(乙)是此过程中汽车拉动重物的功率P随时间t的变化图象,设t=0时汽车开始提升重物,忽略水的重力和滑轮的摩擦,g取10N/kg。求:
(1)圆柱型重物的密度
(2)打捞前,圆柱形重物的上表面所受的水的压力
(3)从打捞开始到圆柱形重物刚刚全部露出水面,汽车共对重物做了多少功
10.一个圆柱形容器放在水平桌面上,在容器中放着一个密度小于水的均匀圆柱体M,且圆柱体M通过细线与圆柱形容器底部相连,如图甲所示(细线未画出)。现慢慢向容器中加水,圆柱形容器内水面高度为h,如图乙所示。测得水面高度h与所加水的质量m的关系如图丙所示。所加水量在3kg以内的过程中无水溢出。(图甲图乙中圆柱体和容器大小,以及细绳的长度不具有暗示意义)求:
(1)由甲图可知圆柱体M刚好漂浮时容器中水的深度h=8cm,请回答圆柱体M的高度H=________ cm。
(2)圆柱体M的密度;
(3)圆柱体M的的重力;
11.盛有适量水的薄壁容器放在水平桌面上(水的密度为ρ0),其底面积为S0。材料不同、体积相同的实心物体A、B用一根无弹性细线连在一起,挂在弹簧测力计下,浸没在容器内的水中,A的上表面刚好与水面相平,如图1所示。现缓慢竖直向上匀速拉动弹簧测力计,测力计的示数F与物体上升的高度h变化图象如图2所示。连接A、B间的绳子所能承受的最大拉力为2F0。求:
(1)物体A受到的重力。
(2)物体A的密度。
(3)整个过程中,水对容器底部压强的最大变化量。
12.测定患者的血沉,是医学上用来帮助医生对病情作出正确判断的一种手段。把新鲜的血液,加入抗凝剂,静置一段时间后形成抗凝血后,红血球即从血浆中分离出来而下沉,设抗凝血是由红血球和血浆组或的悬浮液,血浆的密度p0≈1.0×103kg/m3,红血球的密度p0≈1.3×103kg/m3。将抗凝血放进竖直放置的血沉管内,红血球起初在血浆中加速下沉,然后一直匀速下沉,其匀速下沉的速度称为“血沉”。正常人血沉的值大约是v=12mm/h,如果把红血球近似看作半径为R的小球,它在血浆中下沉时所受的粘滞阻力为f=6πηRv中,已知在室温下η=1.8×10-3Pa·s,已知V球=4/3πR3 , 试根据以上信息解答下列问题。
(1)红血球在血浆中为什么先加速下沉后一直匀速下沉?
(2)计算红血球半径的大小。
13.小明同学想探究某种均匀材料制成的边长为a的实心正方体物块的某些物理特性(如密度、压强等),他先把该物块放入水中,物块静止时,有1/3体积露出水面(如图甲),请根据以上信息解下列问题:
(1)物块的密度ρ物。
(2)物块下表面受到的压强P1。
(3)把物块从水中拿出并擦后放在水平地面上(如图乙),求物块对水平地面的压强
P2 .(要求:本题计算结果要用a、ρ水、g表示,已知水的密度为ρ水)
14.新型电饭锅在煮饭时采用“高温”和“低温”两种方式交替加热,其内部电路如图所示,R1和R2均为电热丝,S1是温度自动控制开关。高、低温挡的额定功率见下表。煮饭时,闭合开关S,电饭锅正常工作30 min消耗的电能为0.44 kW·h。求:
额定电压 220 V
额定功率 低温挡 440 W
高温挡 1100 W
(1)煮饭时通过R1的电流;
(2)电热丝R2的电阻;
(3)30 min内R2消耗的电能。
15.小金用如图所示的实验装置测量杠杆的机械效率。实验时竖直
向上拉动杠杆,使挂在杠杆下面的钩码缓缓上升。(支点和杠杆的摩擦
不计)问:
(1)重为5N的钩码挂在A点时,人的拉力F为4N,钩码上升0.3m
时,动力作用点C上升0.5m,此时机械效率η1为多大?
(2)小金为了进一步研究杠杆的机械效率与哪些因素有关,仍用该实验装置,将钩码移到B点,再次缓慢提升杠杆使动力作用点C仍然上升0.5m.问:人的拉力F与第一次相比 (选填“变大”、“变小”或“不变”)。比较此时的机械效率η1与η2的大小并用学过的知识给予推导。
16.工人用如图甲所示的滑轮组利用箱子运送建材上楼,每次运送量不定。滑轮组的机械效率随重
力不同的建材变化的图象如图乙所示,滑轮与钢绳间的摩擦力及箱子和绳重忽略不计。求:
(1)若工人用300N的拉力,将建材匀速竖直向上提升了4m,工人所做功;
(2)当所运送建材的重为500N时,工人作用在绳子上的拉力;
(3)当滑轮组的机械效率为80%时,所运送建材受到的重力。
物理解答题
1.如图所示,一个内底面积为100 cm2的柱形容器中盛有深度为60 cm的水,水底有一块底面积为50 cm2,高为6 cm的长方体铝块。现用一电动机以恒定不变的输出功率把铝块提出水面并继续提升一段距离。已知铝块浸没在水中时上升速度恒为0.27 m/s。铝的密度为2.7×103 kg/m3,g取10 N/kg,铝块提升过程中受到的阻力、绳子自重和摩擦等都不计。求:
(1)铝块的重力。
(2)把铝块提升到上表面与水面相平所需的时间。
(3)电动机输出功率的大小。
(4)铝块完全露出水面后匀速上升的速度。
(5)铝块从浸没于水中到完全露出水面,水对容器底部压强的减小值。
【答案】(1)长方体铝块的体积
V=Sh=50×10-4 m2×0.06 m=3.0×10-4 m3,
铝块的质量m=ρ铝V=2.7×103 kg/m3×3.0×10-4 m3=0.81 kg,
铝块的重力G=mg=0.81 kg×10 N/kg=8.1 N。
(2)把铝块提升到上表面与水面相平,铝块被提升的距离s=h水-h铝=0.6 m-0.06 m=0.54 m,
由v=可得,提升所需的时间t==2 s。
(3)铝块浸没时受到的浮力
F浮=ρ水gV排=ρ水gV=1.0×103 kg/m3×10 N/kg×3.0×10-4 m3=3 N,
铝块匀速上升时受力平衡,受到浮力、电动机的拉力与铝块的重力,
所以电动机对铝块的拉力
F=G-F浮=8.1 N-3 N=5.1 N,
电动机输出功率
P=Fv=5.1 N×0.27 m/s=1.377 W。
(4)铝块完全露出水面后匀速上升时,电动机对它的拉力F'=G=8.1 N,
电动机输出功率恒定不变,则铝块完全露出水面后匀速上升的速度
v'==0.17 m/s。
(5)铝块从浸没于水中到完全露出水面,排开水的体积减小,水面下降的高度
Δh==3×10-2 m,
所以水对容器底部压强的减小值
Δp=ρ水gΔh=1.0×103 kg/m3×10 N/kg×3×10-2 m=300 Pa。
2.小雨通过如图甲所示滑轮组将水中物体匀速提升至空中,他所用拉力与绳子自由端移动能距离的关系图象如图乙所示。其中物体在空中匀速上升过程中滑轮组的机械效率为.每个滑轮等重,不计绳重、摩擦和水的阻力。(水的密度为求:
(1)物体在空中上升,小雨做的功是多少?
(2)每个滑轮的重力是多少?
(3)物体的密度是多少?
【答案】(1)小雨做的功:;
(2)根据可得,物体在空中上升做的有用功:
,
根据可得,物体的重力:
,
不计绳重、摩擦,物体在空中上升时,拉力,
则,
所以每个滑轮的重力为;
(3)由图乙可知,物体没有露出水面之前,绳端的拉力,
则物体完全浸没时受到的浮力:,
,
物体的质量:,
则物体的密度:。
3.如图所示,一根质量分布均匀的木棒,质量为m,长度为L,竖直挂在转轴O处。在木棒最下端用一方向始终水平向右的拉力F缓慢将木棒拉动到竖直方向夹角为θ的位置(转轴处摩擦不计)。问:。
(1)画出θ=60°时拉力F的力臂L1,并计算力臂的大小。
(2)木棒的重力作用点在其长度二分之一处,随拉开角度θ的增加,拉力F将如何变化?推导拉力F与角度θ的关系式。
【答案】(1)θ=60°时,拉力的力臂L1=Lcosθ=Lcos60°=;
F=mgtanθ。当0<θ<90°时,tanθ随θ的增大而增大,拉力F也随之增大。
4.桥式起重机在工业生产上有广泛应用.如图是某桥式起重机的示意图,水平横梁MN架在轨道A和B上,电动机D可沿横梁左右移动.横梁、电动机、挂钩、滑轮、钢索、导线的质量以及滑轮上的摩擦均不计.
(1)电动机通过滑轮组,将质量为600千克的零件,以0.4米/秒的速度匀速吊高4米.求:电动机对零件做的功为多少焦?电动机的功率至少为多少瓦?(g取10牛/千克)
(2)已知横梁长度为L,零件质量为m,电动机吊着零件从M点出发并开始计时,以水平速度v匀速运动到N点,横梁对轨道A的压力F与时间t的关系式为:F=________.
【答案】 (1)电动机对零件做的功:
W=gh=mgh=600kg×10N/kg×4m=2.4×104J,
因横梁、电动机、挂钩、滑轮、钢索、导线的质量以及滑轮上的摩擦均不计,
所以,拉力做的功即为克服零件重力所做的功,
则电动机对零件做功的功率:
=mgv=600kg×10N/kg×0.4m/s=2.4×103W,
则电动机的最小功率为2.4×103W;
(2)
5.如图所示,在宽为的小方凳上与凳边平行放一轻质硬木棒,木棒左端处悬挂物体甲,右侧悬挂物体乙,使木棒能水平静止。当把悬挂乙的细绳移至点时,木棒恰好将顺时针转动。已知,则要使木棒能水平静止悬挂乙的细绳可移动范围长度是多少?
【答案】当把悬挂乙的细绳移至点时,木棒恰好将顺时针转动,此时支点为,
由杠杆的平衡条件可得,,
则;
当支点位于点且木棒恰好将逆时针转动时,悬挂乙的细绳移至点,
由杠杆的平衡条件可得,,
则,
所以,要使木棒能水平静止悬挂乙的细绳可移动范围长度:
。
6.实验室里可以用欧姆表来直接测量电阻。如图虚线框内是欧姆表的简化结构图,它由灵敏电流表、电源、变阻器等组成。在a、b间接入一个电阻R,路中就有一个对应电流I,即电阻R与电流表的读数I有一一对应关系。所以,由电流表的指针位置可以知道电阻R大小。为了方便,事先在电流表的刻度盘上标出了电阻的欧姆值。欧姆表在测量电阻前都需要调零,即把a、b两接线柱短接,调节变阻器的滑片位置,使电流表满偏(指在最大刻度处)
(1)普通电流表示数标识情况为左小右大,那么改装后的欧姆表示数的标识情况为________。
(2)若某欧姆表的刻度值是按电源电压为1.5V来刻度的,满偏电流为10mA.那么5mA位置时,对应的电阻值为________Ω.在使用一段时间后,发现电源电压降为1.2V,用这个欧姆表测得某电阻为350Ω,则这个电阻的实际值为(不考虑电源本身的电阻)________Ω。
【答案】(1)左大右小(2)150;280
7.如图甲所示是一种家庭水箱水位测量装置示意图,电源电压18V保持不变,电压表量程0 15V,电流表量程0 3A,R0是阻值为10Ω的定值电阻,R1是长20cm、阻值为20Ω的电阻丝,滑片P把电阻丝与轻质弹簧的指针连在一起。圆柱体M长80cm,底面积为200cm2 . 当水位处于最高处时,M刚好浸没在水中,滑片P恰好在R1的最上端。轻质弹簧阻值不计,M全部露出水面前,弹簧的伸长长度△L始终与受到的拉力F成正比,如图乙所示。
(1)如要求电表指针偏转的幅度随水位的上升而增大,则选用电路中________表的示数来显示水位变化。
(2)当水位处于最高处时,电压表的示数为多少?
(3)当水位下降,圆柱体露出水面部分的长度为50cm时,电流表示数为多少?(g取10N/kg)
【答案】(1)电压表
(2)当水位处于最高处时,总电阻为:R总=R1+R0=20Ω+10Ω=30Ω;
此时的总电流;
此时电压表的示数:U1=I1R1=0.6A×20Ω=12V。
(3)当圆柱体露出水面部分的长度为50cm时,
圆柱体减小的V排=Sh=200cm2×50cm=104cm3=0.01m3;
弹簧拉力的增大量为:F浮=ρ液gV排=103kg/m3×10N/kg×0.01m3=100N;
根据乙图可知,此时弹簧向下伸长10cm;
那么变阻器接入电路的阻值:;
此时的总电阻:R总'=R1'+R0=10Ω+10Ω=20Ω;
此时电流表的示数为:。
8.一根金属棒AB置于水平地面上,今通过弹簧测力计竖直地将棒的右端B缓慢拉起,如图甲所示,在此过程中,弹簧测力计对棒所做的功W与B端离开地面的高度x的关系如图乙所示,请根据图象解答下列问题.
(1)该金属棒的长度l=________m;
(2)在B端拉起的过程中,当x1=0.6m时,测力计的示数为F1=________N;当x2=1.6m时,测力计的示数F2=________N.
(3)求金属棒的重心到A端的距离d.
【答案】 (1)1.2
(2)3;5
解:由杠杆平衡条件得,重心到A端的距离d= =0.72m.
9.图(甲)所示是使用汽车打捞水下重物的示意图,汽车通过定滑轮牵引水下一个圆柱形重物,在整个打捞过程中,汽车以恒定的速度V=0.2m/s向右运动。图(乙)是此过程中汽车拉动重物的功率P随时间t的变化图象,设t=0时汽车开始提升重物,忽略水的重力和滑轮的摩擦,g取10N/kg。求:
(1)圆柱型重物的密度
(2)打捞前,圆柱形重物的上表面所受的水的压力
(3)从打捞开始到圆柱形重物刚刚全部露出水面,汽车共对重物做了多少功
【答案】 (1)解:因为P= ,
所以汽车在CD阶段对重物的拉力F1= =4000N,
所以物体受到的重力为G=F1=4000N,
物体的质量为m= =400kg。
同理汽车在AB阶段对重物的拉力为F2= =3500N,
此时物体受到的浮力为F浮=G-F2=4000N-3500N=500N,
物体的体积为V=V排= =5×10-2m3
物体的密度为
(2)解:重物从上表面接触到水面到刚好整个物体全部出水经历的时间为t=60s-50s=10s,
物体的高度h=0.2m/s×10s=2m,
物体的表面积S= ,
由图乙AB阶段可知,物体从水底上升到上表面刚好接触水面用时50s,
上升高度为H= 0.2m/s×50s=10m,
所以水对上表面产生的压力
F压=pS=ρ水gHS=1×103kg/m3×10N/kg×10m×2.5×10-2m2=2.5×103N。
(3)解:从开始到捞到物体上表面露出水面拉力做的功为W1=PAB×t1=700W×50s=35000J;
物体从上表面露出水面到完全离开水面拉力做的功为
W2=△P×t2= =3500J,
整个打捞过程拉力做的功为W=W1+W2=35000J+7500J=42500J。
10.一个圆柱形容器放在水平桌面上,在容器中放着一个密度小于水的均匀圆柱体M,且圆柱体M通过细线与圆柱形容器底部相连,如图甲所示(细线未画出)。现慢慢向容器中加水,圆柱形容器内水面高度为h,如图乙所示。测得水面高度h与所加水的质量m的关系如图丙所示。所加水量在3kg以内的过程中无水溢出。(图甲图乙中圆柱体和容器大小,以及细绳的长度不具有暗示意义)求:
(1)由甲图可知圆柱体M刚好漂浮时容器中水的深度h=8cm,请回答圆柱体M的高度H=________ cm。
(2)圆柱体M的密度;
(3)圆柱体M的的重力;
【答案】 (1)10
(2)当圆柱体飘浮时:F浮=G
ρ水gSh高=ρ物gSH 1000kg/m3×gS×0.08m=×ρ物gS×0.1m
得ρ物=800kg/m3
(3)由图得,当容器内水的深度从8cm到12cm时,
水的体积增加量:△V=△m/ρ水=1kg/1000kg/m3=0.001m3
在这个过程中,圆柱体一直处于漂浮状态,即S容=△V/△h=0.001m3/0.04m=0.025m2
由图得,当容器内水的深度从0cm到8cm时,
水的体积增加量:△V’=△m’/ρ水=0.8kg/1000kg/m3=0.0008m3
在圆柱体漂浮前,S容-S圆=△V’/△h’=0.0008m3/0.08m=0.01m2
即S圆=0.015m2
G=ρ物gS圆H=800kg/m3×10N/kg×0.015m2×0.08m=12N
11.盛有适量水的薄壁容器放在水平桌面上(水的密度为ρ0),其底面积为S0。材料不同、体积相同的实心物体A、B用一根无弹性细线连在一起,挂在弹簧测力计下,浸没在容器内的水中,A的上表面刚好与水面相平,如图1所示。现缓慢竖直向上匀速拉动弹簧测力计,测力计的示数F与物体上升的高度h变化图象如图2所示。连接A、B间的绳子所能承受的最大拉力为2F0。求:
(1)物体A受到的重力。
(2)物体A的密度。
(3)整个过程中,水对容器底部压强的最大变化量。
【答案】 (1)物体A受到的重力GA=F0;
(2)物体A的体积:;
物体A的密度:。
(3)总浮力的最大变化量:△F浮=F浮总-F浮总′=GA+F0=2F0 ,
排开水的体积的最大变化量:;
则容器内水的深度的最大变化量:;
所以水对容器底部压强的最大变化量:。
12.测定患者的血沉,是医学上用来帮助医生对病情作出正确判断的一种手段。把新鲜的血液,加入抗凝剂,静置一段时间后形成抗凝血后,红血球即从血浆中分离出来而下沉,设抗凝血是由红血球和血浆组或的悬浮液,血浆的密度p0≈1.0×103kg/m3,红血球的密度p0≈1.3×103kg/m3。将抗凝血放进竖直放置的血沉管内,红血球起初在血浆中加速下沉,然后一直匀速下沉,其匀速下沉的速度称为“血沉”。正常人血沉的值大约是v=12mm/h,如果把红血球近似看作半径为R的小球,它在血浆中下沉时所受的粘滞阻力为f=6πηRv中,已知在室温下η=1.8×10-3Pa·s,已知V球=4/3πR3 , 试根据以上信息解答下列问题。
(1)红血球在血浆中为什么先加速下沉后一直匀速下沉?
(2)计算红血球半径的大小。
【答案】 (1)解:由于血浆的密度ρ0小于红血球的密度ρ,红血球受到的浮力小于重力,所以会加速下沉,随着红血球下沉速度变大,根据f=6πrRv可知粘滞阻力增大,当f+F浮=G时,红血球就会匀速下沉。
(2)解:当红血球在血浆中匀速下沉时,f+F浮=G F浮=G排=ρ0V排g= ρ0× πR3g= πρgR3 G=mg=ρV球g= × πR3g= πρgR3
代入得:6πηRv+ πρ0gR3 = πρgR3
所以:R=
将η=1.8×10-3Pa s ν=12mm/h= ×10-5m/s,
ρ0=1.0×103kg/m3,g=10N/kg代入并计算得:R=3×10-6m
13.小明同学想探究某种均匀材料制成的边长为a的实心正方体物块的某些物理特性(如密度、压强等),他先把该物块放入水中,物块静止时,有1/3体积露出水面(如图甲),请根据以上信息解下列问题:
(1)物块的密度ρ物。
(2)物块下表面受到的压强P1。
(3)把物块从水中拿出并擦后放在水平地面上(如图乙),求物块对水平地面的压强
P2 .(要求:本题计算结果要用a、ρ水、g表示,已知水的密度为ρ水)
【答案】 (1)因为F浮=G,所以ρ水g(1﹣ )V=ρ物Vg
ρ物= ρ水= ×1g/cm3≈0.67g/cm3
答:物体密度为0.67g/cm3
(2)下表面受到的压强P=ρ水gh= ρ水ga
(3)物体的底面积为S=a2 , 物体对地面的压力为F=G=ρ物ga3 ,
物体对水平地面的压强为P= = =ρ物ga
14.新型电饭锅在煮饭时采用“高温”和“低温”两种方式交替加热,其内部电路如图所示,R1和R2均为电热丝,S1是温度自动控制开关。高、低温挡的额定功率见下表。煮饭时,闭合开关S,电饭锅正常工作30 min消耗的电能为0.44 kW·h。求:
额定电压 220 V
额定功率 低温挡 440 W
高温挡 1100 W
(1)煮饭时通过R1的电流;
(2)电热丝R2的电阻;
(3)30 min内R2消耗的电能。
【答案】(1)当S、S1都闭合时是高温挡,当只S闭合时是低温挡,此时P低=P1=440 W
煮饭时通过R1的电流I1===2 A
(2)电饭锅正常工作时,R2的功率为P2=P高-P1=1 100 W-440 W=660 W
通过R2的电流I2===3 A
R2的电阻为R2==≈73.3 Ω
(3)因为煮饭时电饭锅交替加热,R1始终工作,R1正常工作30 min消耗的电能为
W1=P1t=0.44 kW×0.5 h=0.22 kW·h
则30 min内R2消耗的电能为:W2=W-W1=0.44 kW·h-0.22 kW·h=0.22 kW·h
15.小金用如图所示的实验装置测量杠杆的机械效率。实验时竖直
向上拉动杠杆,使挂在杠杆下面的钩码缓缓上升。(支点和杠杆的摩擦
不计)问:
(1)重为5N的钩码挂在A点时,人的拉力F为4N,钩码上升0.3m
时,动力作用点C上升0.5m,此时机械效率η1为多大?
(2)小金为了进一步研究杠杆的机械效率与哪些因素有关,仍用该实验装置,将钩码移到B点,再次缓慢提升杠杆使动力作用点C仍然上升0.5m.问:人的拉力F与第一次相比 (选填“变大”、“变小”或“不变”)。比较此时的机械效率η1与η2的大小并用学过的知识给予推导。
【答案】(1)杠杆的有用功为提升钩码做的功,W有=Gh1=5×0.3m=1.5J,人拉力做的功为总功,W总=Fh2=4N×0.5m=2J,故机械效率η1=W有/W总×100%=1.5J/2J×100%=75%;
(2)F变小;
因为第二次动力作用点C仍然上升0.5m,故杠杆提升至原来的高度,而杠杆的额外功为提升杠杆自重做的功,W额=Goho,其大小不变;但因钩码移至B点,故钩码提升的高度减小,所以有用功W有=Gh1减小;综上所述,第二次有用功减小,额外功不变,故机械效率变小,所以η1>η2。
16.工人用如图甲所示的滑轮组利用箱子运送建材上楼,每次运送量不定。滑轮组的机械效率随重
力不同的建材变化的图象如图乙所示,滑轮与钢绳间的摩擦力及箱子和绳重忽略不计。求:
(1)若工人用300N的拉力,将建材匀速竖直向上提升了4m,工人所做功;
(2)当所运送建材的重为500N时,工人作用在绳子上的拉力;
(3)当滑轮组的机械效率为80%时,所运送建材受到的重力。
【答案】(1)拉力移动距离:s=nh=2×4m=8m,
拉力做功:W=Fs=300N×8m=2400J; (2分)
(2)由图乙可知,建材的重为500N时,滑轮组机械效率为50%,
由η====得,建材的重为500N时,工人作用在绳子上的拉力;
F==500N; (2分)
(3)由F=(G+G动)得,动滑轮重:G动=2F﹣G=2×500N﹣500N=500N,
由η====得当机械效率为80%时,所运送建材受到的重力:
G′==2000N。 (2分)
1.如图所示,一个内底面积为100 cm2的柱形容器中盛有深度为60 cm的水,水底有一块底面积为50 cm2,高为6 cm的长方体铝块。现用一电动机以恒定不变的输出功率把铝块提出水面并继续提升一段距离。已知铝块浸没在水中时上升速度恒为0.27 m/s。铝的密度为2.7×103 kg/m3,g取10 N/kg,铝块提升过程中受到的阻力、绳子自重和摩擦等都不计。求:
(1)铝块的重力。
(2)把铝块提升到上表面与水面相平所需的时间。
(3)电动机输出功率的大小。
(4)铝块完全露出水面后匀速上升的速度。
(5)铝块从浸没于水中到完全露出水面,水对容器底部压强的减小值。
2.小雨通过如图甲所示滑轮组将水中物体匀速提升至空中,他所用拉力与绳子自由端移动能距离的关系图象如图乙所示。其中物体在空中匀速上升过程中滑轮组的机械效率为.每个滑轮等重,不计绳重、摩擦和水的阻力。(水的密度为求:
(1)物体在空中上升,小雨做的功是多少?
(2)每个滑轮的重力是多少?
(3)物体的密度是多少?
3.如图所示,一根质量分布均匀的木棒,质量为m,长度为L,竖直挂在转轴O处。在木棒最下端用一方向始终水平向右的拉力F缓慢将木棒拉动到竖直方向夹角为θ的位置(转轴处摩擦不计)。问:。
(1)画出θ=60°时拉力F的力臂L1,并计算力臂的大小。
(2)木棒的重力作用点在其长度二分之一处,随拉开角度θ的增加,拉力F将如何变化?推导拉力F与角度θ的关系式。
4.桥式起重机在工业生产上有广泛应用.如图是某桥式起重机的示意图,水平横梁MN架在轨道A和B上,电动机D可沿横梁左右移动.横梁、电动机、挂钩、滑轮、钢索、导线的质量以及滑轮上的摩擦均不计.
(1)电动机通过滑轮组,将质量为600千克的零件,以0.4米/秒的速度匀速吊高4米.求:电动机对零件做的功为多少焦?电动机的功率至少为多少瓦?(g取10牛/千克)
(2)已知横梁长度为L,零件质量为m,电动机吊着零件从M点出发并开始计时,以水平速度v匀速运动到N点,横梁对轨道A的压力F与时间t的关系式为:F=________.
5.如图所示,在宽为的小方凳上与凳边平行放一轻质硬木棒,木棒左端处悬挂物体甲,右侧悬挂物体乙,使木棒能水平静止。当把悬挂乙的细绳移至点时,木棒恰好将顺时针转动。已知,则要使木棒能水平静止悬挂乙的细绳可移动范围长度是多少?
6.实验室里可以用欧姆表来直接测量电阻。如图虚线框内是欧姆表的简化结构图,它由灵敏电流表、电源、变阻器等组成。在a、b间接入一个电阻R,路中就有一个对应电流I,即电阻R与电流表的读数I有一一对应关系。所以,由电流表的指针位置可以知道电阻R大小。为了方便,事先在电流表的刻度盘上标出了电阻的欧姆值。欧姆表在测量电阻前都需要调零,即把a、b两接线柱短接,调节变阻器的滑片位置,使电流表满偏(指在最大刻度处)
(1)普通电流表示数标识情况为左小右大,那么改装后的欧姆表示数的标识情况为________。
(2)若某欧姆表的刻度值是按电源电压为1.5V来刻度的,满偏电流为10mA.那么5mA位置时,对应的电阻值为________Ω.在使用一段时间后,发现电源电压降为1.2V,用这个欧姆表测得某电阻为350Ω,则这个电阻的实际值为(不考虑电源本身的电阻)________Ω。
7.如图甲所示是一种家庭水箱水位测量装置示意图,电源电压18V保持不变,电压表量程0 15V,电流表量程0 3A,R0是阻值为10Ω的定值电阻,R1是长20cm、阻值为20Ω的电阻丝,滑片P把电阻丝与轻质弹簧的指针连在一起。圆柱体M长80cm,底面积为200cm2 . 当水位处于最高处时,M刚好浸没在水中,滑片P恰好在R1的最上端。轻质弹簧阻值不计,M全部露出水面前,弹簧的伸长长度△L始终与受到的拉力F成正比,如图乙所示。
(1)如要求电表指针偏转的幅度随水位的上升而增大,则选用电路中________表的示数来显示水位变化。
(2)当水位处于最高处时,电压表的示数为多少?
(3)当水位下降,圆柱体露出水面部分的长度为50cm时,电流表示数为多少?(g取10N/kg)
8.一根金属棒AB置于水平地面上,今通过弹簧测力计竖直地将棒的右端B缓慢拉起,如图甲所示,在此过程中,弹簧测力计对棒所做的功W与B端离开地面的高度x的关系如图乙所示,请根据图象解答下列问题.
(1)该金属棒的长度l=________m;
(2)在B端拉起的过程中,当x1=0.6m时,测力计的示数为F1=________N;当x2=1.6m时,测力计的示数F2=________N.
(3)求金属棒的重心到A端的距离d.
9.图(甲)所示是使用汽车打捞水下重物的示意图,汽车通过定滑轮牵引水下一个圆柱形重物,在整个打捞过程中,汽车以恒定的速度V=0.2m/s向右运动。图(乙)是此过程中汽车拉动重物的功率P随时间t的变化图象,设t=0时汽车开始提升重物,忽略水的重力和滑轮的摩擦,g取10N/kg。求:
(1)圆柱型重物的密度
(2)打捞前,圆柱形重物的上表面所受的水的压力
(3)从打捞开始到圆柱形重物刚刚全部露出水面,汽车共对重物做了多少功
10.一个圆柱形容器放在水平桌面上,在容器中放着一个密度小于水的均匀圆柱体M,且圆柱体M通过细线与圆柱形容器底部相连,如图甲所示(细线未画出)。现慢慢向容器中加水,圆柱形容器内水面高度为h,如图乙所示。测得水面高度h与所加水的质量m的关系如图丙所示。所加水量在3kg以内的过程中无水溢出。(图甲图乙中圆柱体和容器大小,以及细绳的长度不具有暗示意义)求:
(1)由甲图可知圆柱体M刚好漂浮时容器中水的深度h=8cm,请回答圆柱体M的高度H=________ cm。
(2)圆柱体M的密度;
(3)圆柱体M的的重力;
11.盛有适量水的薄壁容器放在水平桌面上(水的密度为ρ0),其底面积为S0。材料不同、体积相同的实心物体A、B用一根无弹性细线连在一起,挂在弹簧测力计下,浸没在容器内的水中,A的上表面刚好与水面相平,如图1所示。现缓慢竖直向上匀速拉动弹簧测力计,测力计的示数F与物体上升的高度h变化图象如图2所示。连接A、B间的绳子所能承受的最大拉力为2F0。求:
(1)物体A受到的重力。
(2)物体A的密度。
(3)整个过程中,水对容器底部压强的最大变化量。
12.测定患者的血沉,是医学上用来帮助医生对病情作出正确判断的一种手段。把新鲜的血液,加入抗凝剂,静置一段时间后形成抗凝血后,红血球即从血浆中分离出来而下沉,设抗凝血是由红血球和血浆组或的悬浮液,血浆的密度p0≈1.0×103kg/m3,红血球的密度p0≈1.3×103kg/m3。将抗凝血放进竖直放置的血沉管内,红血球起初在血浆中加速下沉,然后一直匀速下沉,其匀速下沉的速度称为“血沉”。正常人血沉的值大约是v=12mm/h,如果把红血球近似看作半径为R的小球,它在血浆中下沉时所受的粘滞阻力为f=6πηRv中,已知在室温下η=1.8×10-3Pa·s,已知V球=4/3πR3 , 试根据以上信息解答下列问题。
(1)红血球在血浆中为什么先加速下沉后一直匀速下沉?
(2)计算红血球半径的大小。
13.小明同学想探究某种均匀材料制成的边长为a的实心正方体物块的某些物理特性(如密度、压强等),他先把该物块放入水中,物块静止时,有1/3体积露出水面(如图甲),请根据以上信息解下列问题:
(1)物块的密度ρ物。
(2)物块下表面受到的压强P1。
(3)把物块从水中拿出并擦后放在水平地面上(如图乙),求物块对水平地面的压强
P2 .(要求:本题计算结果要用a、ρ水、g表示,已知水的密度为ρ水)
14.新型电饭锅在煮饭时采用“高温”和“低温”两种方式交替加热,其内部电路如图所示,R1和R2均为电热丝,S1是温度自动控制开关。高、低温挡的额定功率见下表。煮饭时,闭合开关S,电饭锅正常工作30 min消耗的电能为0.44 kW·h。求:
额定电压 220 V
额定功率 低温挡 440 W
高温挡 1100 W
(1)煮饭时通过R1的电流;
(2)电热丝R2的电阻;
(3)30 min内R2消耗的电能。
15.小金用如图所示的实验装置测量杠杆的机械效率。实验时竖直
向上拉动杠杆,使挂在杠杆下面的钩码缓缓上升。(支点和杠杆的摩擦
不计)问:
(1)重为5N的钩码挂在A点时,人的拉力F为4N,钩码上升0.3m
时,动力作用点C上升0.5m,此时机械效率η1为多大?
(2)小金为了进一步研究杠杆的机械效率与哪些因素有关,仍用该实验装置,将钩码移到B点,再次缓慢提升杠杆使动力作用点C仍然上升0.5m.问:人的拉力F与第一次相比 (选填“变大”、“变小”或“不变”)。比较此时的机械效率η1与η2的大小并用学过的知识给予推导。
16.工人用如图甲所示的滑轮组利用箱子运送建材上楼,每次运送量不定。滑轮组的机械效率随重
力不同的建材变化的图象如图乙所示,滑轮与钢绳间的摩擦力及箱子和绳重忽略不计。求:
(1)若工人用300N的拉力,将建材匀速竖直向上提升了4m,工人所做功;
(2)当所运送建材的重为500N时,工人作用在绳子上的拉力;
(3)当滑轮组的机械效率为80%时,所运送建材受到的重力。
物理解答题
1.如图所示,一个内底面积为100 cm2的柱形容器中盛有深度为60 cm的水,水底有一块底面积为50 cm2,高为6 cm的长方体铝块。现用一电动机以恒定不变的输出功率把铝块提出水面并继续提升一段距离。已知铝块浸没在水中时上升速度恒为0.27 m/s。铝的密度为2.7×103 kg/m3,g取10 N/kg,铝块提升过程中受到的阻力、绳子自重和摩擦等都不计。求:
(1)铝块的重力。
(2)把铝块提升到上表面与水面相平所需的时间。
(3)电动机输出功率的大小。
(4)铝块完全露出水面后匀速上升的速度。
(5)铝块从浸没于水中到完全露出水面,水对容器底部压强的减小值。
【答案】(1)长方体铝块的体积
V=Sh=50×10-4 m2×0.06 m=3.0×10-4 m3,
铝块的质量m=ρ铝V=2.7×103 kg/m3×3.0×10-4 m3=0.81 kg,
铝块的重力G=mg=0.81 kg×10 N/kg=8.1 N。
(2)把铝块提升到上表面与水面相平,铝块被提升的距离s=h水-h铝=0.6 m-0.06 m=0.54 m,
由v=可得,提升所需的时间t==2 s。
(3)铝块浸没时受到的浮力
F浮=ρ水gV排=ρ水gV=1.0×103 kg/m3×10 N/kg×3.0×10-4 m3=3 N,
铝块匀速上升时受力平衡,受到浮力、电动机的拉力与铝块的重力,
所以电动机对铝块的拉力
F=G-F浮=8.1 N-3 N=5.1 N,
电动机输出功率
P=Fv=5.1 N×0.27 m/s=1.377 W。
(4)铝块完全露出水面后匀速上升时,电动机对它的拉力F'=G=8.1 N,
电动机输出功率恒定不变,则铝块完全露出水面后匀速上升的速度
v'==0.17 m/s。
(5)铝块从浸没于水中到完全露出水面,排开水的体积减小,水面下降的高度
Δh==3×10-2 m,
所以水对容器底部压强的减小值
Δp=ρ水gΔh=1.0×103 kg/m3×10 N/kg×3×10-2 m=300 Pa。
2.小雨通过如图甲所示滑轮组将水中物体匀速提升至空中,他所用拉力与绳子自由端移动能距离的关系图象如图乙所示。其中物体在空中匀速上升过程中滑轮组的机械效率为.每个滑轮等重,不计绳重、摩擦和水的阻力。(水的密度为求:
(1)物体在空中上升,小雨做的功是多少?
(2)每个滑轮的重力是多少?
(3)物体的密度是多少?
【答案】(1)小雨做的功:;
(2)根据可得,物体在空中上升做的有用功:
,
根据可得,物体的重力:
,
不计绳重、摩擦,物体在空中上升时,拉力,
则,
所以每个滑轮的重力为;
(3)由图乙可知,物体没有露出水面之前,绳端的拉力,
则物体完全浸没时受到的浮力:,
,
物体的质量:,
则物体的密度:。
3.如图所示,一根质量分布均匀的木棒,质量为m,长度为L,竖直挂在转轴O处。在木棒最下端用一方向始终水平向右的拉力F缓慢将木棒拉动到竖直方向夹角为θ的位置(转轴处摩擦不计)。问:。
(1)画出θ=60°时拉力F的力臂L1,并计算力臂的大小。
(2)木棒的重力作用点在其长度二分之一处,随拉开角度θ的增加,拉力F将如何变化?推导拉力F与角度θ的关系式。
【答案】(1)θ=60°时,拉力的力臂L1=Lcosθ=Lcos60°=;
F=mgtanθ。当0<θ<90°时,tanθ随θ的增大而增大,拉力F也随之增大。
4.桥式起重机在工业生产上有广泛应用.如图是某桥式起重机的示意图,水平横梁MN架在轨道A和B上,电动机D可沿横梁左右移动.横梁、电动机、挂钩、滑轮、钢索、导线的质量以及滑轮上的摩擦均不计.
(1)电动机通过滑轮组,将质量为600千克的零件,以0.4米/秒的速度匀速吊高4米.求:电动机对零件做的功为多少焦?电动机的功率至少为多少瓦?(g取10牛/千克)
(2)已知横梁长度为L,零件质量为m,电动机吊着零件从M点出发并开始计时,以水平速度v匀速运动到N点,横梁对轨道A的压力F与时间t的关系式为:F=________.
【答案】 (1)电动机对零件做的功:
W=gh=mgh=600kg×10N/kg×4m=2.4×104J,
因横梁、电动机、挂钩、滑轮、钢索、导线的质量以及滑轮上的摩擦均不计,
所以,拉力做的功即为克服零件重力所做的功,
则电动机对零件做功的功率:
=mgv=600kg×10N/kg×0.4m/s=2.4×103W,
则电动机的最小功率为2.4×103W;
(2)
5.如图所示,在宽为的小方凳上与凳边平行放一轻质硬木棒,木棒左端处悬挂物体甲,右侧悬挂物体乙,使木棒能水平静止。当把悬挂乙的细绳移至点时,木棒恰好将顺时针转动。已知,则要使木棒能水平静止悬挂乙的细绳可移动范围长度是多少?
【答案】当把悬挂乙的细绳移至点时,木棒恰好将顺时针转动,此时支点为,
由杠杆的平衡条件可得,,
则;
当支点位于点且木棒恰好将逆时针转动时,悬挂乙的细绳移至点,
由杠杆的平衡条件可得,,
则,
所以,要使木棒能水平静止悬挂乙的细绳可移动范围长度:
。
6.实验室里可以用欧姆表来直接测量电阻。如图虚线框内是欧姆表的简化结构图,它由灵敏电流表、电源、变阻器等组成。在a、b间接入一个电阻R,路中就有一个对应电流I,即电阻R与电流表的读数I有一一对应关系。所以,由电流表的指针位置可以知道电阻R大小。为了方便,事先在电流表的刻度盘上标出了电阻的欧姆值。欧姆表在测量电阻前都需要调零,即把a、b两接线柱短接,调节变阻器的滑片位置,使电流表满偏(指在最大刻度处)
(1)普通电流表示数标识情况为左小右大,那么改装后的欧姆表示数的标识情况为________。
(2)若某欧姆表的刻度值是按电源电压为1.5V来刻度的,满偏电流为10mA.那么5mA位置时,对应的电阻值为________Ω.在使用一段时间后,发现电源电压降为1.2V,用这个欧姆表测得某电阻为350Ω,则这个电阻的实际值为(不考虑电源本身的电阻)________Ω。
【答案】(1)左大右小(2)150;280
7.如图甲所示是一种家庭水箱水位测量装置示意图,电源电压18V保持不变,电压表量程0 15V,电流表量程0 3A,R0是阻值为10Ω的定值电阻,R1是长20cm、阻值为20Ω的电阻丝,滑片P把电阻丝与轻质弹簧的指针连在一起。圆柱体M长80cm,底面积为200cm2 . 当水位处于最高处时,M刚好浸没在水中,滑片P恰好在R1的最上端。轻质弹簧阻值不计,M全部露出水面前,弹簧的伸长长度△L始终与受到的拉力F成正比,如图乙所示。
(1)如要求电表指针偏转的幅度随水位的上升而增大,则选用电路中________表的示数来显示水位变化。
(2)当水位处于最高处时,电压表的示数为多少?
(3)当水位下降,圆柱体露出水面部分的长度为50cm时,电流表示数为多少?(g取10N/kg)
【答案】(1)电压表
(2)当水位处于最高处时,总电阻为:R总=R1+R0=20Ω+10Ω=30Ω;
此时的总电流;
此时电压表的示数:U1=I1R1=0.6A×20Ω=12V。
(3)当圆柱体露出水面部分的长度为50cm时,
圆柱体减小的V排=Sh=200cm2×50cm=104cm3=0.01m3;
弹簧拉力的增大量为:F浮=ρ液gV排=103kg/m3×10N/kg×0.01m3=100N;
根据乙图可知,此时弹簧向下伸长10cm;
那么变阻器接入电路的阻值:;
此时的总电阻:R总'=R1'+R0=10Ω+10Ω=20Ω;
此时电流表的示数为:。
8.一根金属棒AB置于水平地面上,今通过弹簧测力计竖直地将棒的右端B缓慢拉起,如图甲所示,在此过程中,弹簧测力计对棒所做的功W与B端离开地面的高度x的关系如图乙所示,请根据图象解答下列问题.
(1)该金属棒的长度l=________m;
(2)在B端拉起的过程中,当x1=0.6m时,测力计的示数为F1=________N;当x2=1.6m时,测力计的示数F2=________N.
(3)求金属棒的重心到A端的距离d.
【答案】 (1)1.2
(2)3;5
解:由杠杆平衡条件得,重心到A端的距离d= =0.72m.
9.图(甲)所示是使用汽车打捞水下重物的示意图,汽车通过定滑轮牵引水下一个圆柱形重物,在整个打捞过程中,汽车以恒定的速度V=0.2m/s向右运动。图(乙)是此过程中汽车拉动重物的功率P随时间t的变化图象,设t=0时汽车开始提升重物,忽略水的重力和滑轮的摩擦,g取10N/kg。求:
(1)圆柱型重物的密度
(2)打捞前,圆柱形重物的上表面所受的水的压力
(3)从打捞开始到圆柱形重物刚刚全部露出水面,汽车共对重物做了多少功
【答案】 (1)解:因为P= ,
所以汽车在CD阶段对重物的拉力F1= =4000N,
所以物体受到的重力为G=F1=4000N,
物体的质量为m= =400kg。
同理汽车在AB阶段对重物的拉力为F2= =3500N,
此时物体受到的浮力为F浮=G-F2=4000N-3500N=500N,
物体的体积为V=V排= =5×10-2m3
物体的密度为
(2)解:重物从上表面接触到水面到刚好整个物体全部出水经历的时间为t=60s-50s=10s,
物体的高度h=0.2m/s×10s=2m,
物体的表面积S= ,
由图乙AB阶段可知,物体从水底上升到上表面刚好接触水面用时50s,
上升高度为H= 0.2m/s×50s=10m,
所以水对上表面产生的压力
F压=pS=ρ水gHS=1×103kg/m3×10N/kg×10m×2.5×10-2m2=2.5×103N。
(3)解:从开始到捞到物体上表面露出水面拉力做的功为W1=PAB×t1=700W×50s=35000J;
物体从上表面露出水面到完全离开水面拉力做的功为
W2=△P×t2= =3500J,
整个打捞过程拉力做的功为W=W1+W2=35000J+7500J=42500J。
10.一个圆柱形容器放在水平桌面上,在容器中放着一个密度小于水的均匀圆柱体M,且圆柱体M通过细线与圆柱形容器底部相连,如图甲所示(细线未画出)。现慢慢向容器中加水,圆柱形容器内水面高度为h,如图乙所示。测得水面高度h与所加水的质量m的关系如图丙所示。所加水量在3kg以内的过程中无水溢出。(图甲图乙中圆柱体和容器大小,以及细绳的长度不具有暗示意义)求:
(1)由甲图可知圆柱体M刚好漂浮时容器中水的深度h=8cm,请回答圆柱体M的高度H=________ cm。
(2)圆柱体M的密度;
(3)圆柱体M的的重力;
【答案】 (1)10
(2)当圆柱体飘浮时:F浮=G
ρ水gSh高=ρ物gSH 1000kg/m3×gS×0.08m=×ρ物gS×0.1m
得ρ物=800kg/m3
(3)由图得,当容器内水的深度从8cm到12cm时,
水的体积增加量:△V=△m/ρ水=1kg/1000kg/m3=0.001m3
在这个过程中,圆柱体一直处于漂浮状态,即S容=△V/△h=0.001m3/0.04m=0.025m2
由图得,当容器内水的深度从0cm到8cm时,
水的体积增加量:△V’=△m’/ρ水=0.8kg/1000kg/m3=0.0008m3
在圆柱体漂浮前,S容-S圆=△V’/△h’=0.0008m3/0.08m=0.01m2
即S圆=0.015m2
G=ρ物gS圆H=800kg/m3×10N/kg×0.015m2×0.08m=12N
11.盛有适量水的薄壁容器放在水平桌面上(水的密度为ρ0),其底面积为S0。材料不同、体积相同的实心物体A、B用一根无弹性细线连在一起,挂在弹簧测力计下,浸没在容器内的水中,A的上表面刚好与水面相平,如图1所示。现缓慢竖直向上匀速拉动弹簧测力计,测力计的示数F与物体上升的高度h变化图象如图2所示。连接A、B间的绳子所能承受的最大拉力为2F0。求:
(1)物体A受到的重力。
(2)物体A的密度。
(3)整个过程中,水对容器底部压强的最大变化量。
【答案】 (1)物体A受到的重力GA=F0;
(2)物体A的体积:;
物体A的密度:。
(3)总浮力的最大变化量:△F浮=F浮总-F浮总′=GA+F0=2F0 ,
排开水的体积的最大变化量:;
则容器内水的深度的最大变化量:;
所以水对容器底部压强的最大变化量:。
12.测定患者的血沉,是医学上用来帮助医生对病情作出正确判断的一种手段。把新鲜的血液,加入抗凝剂,静置一段时间后形成抗凝血后,红血球即从血浆中分离出来而下沉,设抗凝血是由红血球和血浆组或的悬浮液,血浆的密度p0≈1.0×103kg/m3,红血球的密度p0≈1.3×103kg/m3。将抗凝血放进竖直放置的血沉管内,红血球起初在血浆中加速下沉,然后一直匀速下沉,其匀速下沉的速度称为“血沉”。正常人血沉的值大约是v=12mm/h,如果把红血球近似看作半径为R的小球,它在血浆中下沉时所受的粘滞阻力为f=6πηRv中,已知在室温下η=1.8×10-3Pa·s,已知V球=4/3πR3 , 试根据以上信息解答下列问题。
(1)红血球在血浆中为什么先加速下沉后一直匀速下沉?
(2)计算红血球半径的大小。
【答案】 (1)解:由于血浆的密度ρ0小于红血球的密度ρ,红血球受到的浮力小于重力,所以会加速下沉,随着红血球下沉速度变大,根据f=6πrRv可知粘滞阻力增大,当f+F浮=G时,红血球就会匀速下沉。
(2)解:当红血球在血浆中匀速下沉时,f+F浮=G F浮=G排=ρ0V排g= ρ0× πR3g= πρgR3 G=mg=ρV球g= × πR3g= πρgR3
代入得:6πηRv+ πρ0gR3 = πρgR3
所以:R=
将η=1.8×10-3Pa s ν=12mm/h= ×10-5m/s,
ρ0=1.0×103kg/m3,g=10N/kg代入并计算得:R=3×10-6m
13.小明同学想探究某种均匀材料制成的边长为a的实心正方体物块的某些物理特性(如密度、压强等),他先把该物块放入水中,物块静止时,有1/3体积露出水面(如图甲),请根据以上信息解下列问题:
(1)物块的密度ρ物。
(2)物块下表面受到的压强P1。
(3)把物块从水中拿出并擦后放在水平地面上(如图乙),求物块对水平地面的压强
P2 .(要求:本题计算结果要用a、ρ水、g表示,已知水的密度为ρ水)
【答案】 (1)因为F浮=G,所以ρ水g(1﹣ )V=ρ物Vg
ρ物= ρ水= ×1g/cm3≈0.67g/cm3
答:物体密度为0.67g/cm3
(2)下表面受到的压强P=ρ水gh= ρ水ga
(3)物体的底面积为S=a2 , 物体对地面的压力为F=G=ρ物ga3 ,
物体对水平地面的压强为P= = =ρ物ga
14.新型电饭锅在煮饭时采用“高温”和“低温”两种方式交替加热,其内部电路如图所示,R1和R2均为电热丝,S1是温度自动控制开关。高、低温挡的额定功率见下表。煮饭时,闭合开关S,电饭锅正常工作30 min消耗的电能为0.44 kW·h。求:
额定电压 220 V
额定功率 低温挡 440 W
高温挡 1100 W
(1)煮饭时通过R1的电流;
(2)电热丝R2的电阻;
(3)30 min内R2消耗的电能。
【答案】(1)当S、S1都闭合时是高温挡,当只S闭合时是低温挡,此时P低=P1=440 W
煮饭时通过R1的电流I1===2 A
(2)电饭锅正常工作时,R2的功率为P2=P高-P1=1 100 W-440 W=660 W
通过R2的电流I2===3 A
R2的电阻为R2==≈73.3 Ω
(3)因为煮饭时电饭锅交替加热,R1始终工作,R1正常工作30 min消耗的电能为
W1=P1t=0.44 kW×0.5 h=0.22 kW·h
则30 min内R2消耗的电能为:W2=W-W1=0.44 kW·h-0.22 kW·h=0.22 kW·h
15.小金用如图所示的实验装置测量杠杆的机械效率。实验时竖直
向上拉动杠杆,使挂在杠杆下面的钩码缓缓上升。(支点和杠杆的摩擦
不计)问:
(1)重为5N的钩码挂在A点时,人的拉力F为4N,钩码上升0.3m
时,动力作用点C上升0.5m,此时机械效率η1为多大?
(2)小金为了进一步研究杠杆的机械效率与哪些因素有关,仍用该实验装置,将钩码移到B点,再次缓慢提升杠杆使动力作用点C仍然上升0.5m.问:人的拉力F与第一次相比 (选填“变大”、“变小”或“不变”)。比较此时的机械效率η1与η2的大小并用学过的知识给予推导。
【答案】(1)杠杆的有用功为提升钩码做的功,W有=Gh1=5×0.3m=1.5J,人拉力做的功为总功,W总=Fh2=4N×0.5m=2J,故机械效率η1=W有/W总×100%=1.5J/2J×100%=75%;
(2)F变小;
因为第二次动力作用点C仍然上升0.5m,故杠杆提升至原来的高度,而杠杆的额外功为提升杠杆自重做的功,W额=Goho,其大小不变;但因钩码移至B点,故钩码提升的高度减小,所以有用功W有=Gh1减小;综上所述,第二次有用功减小,额外功不变,故机械效率变小,所以η1>η2。
16.工人用如图甲所示的滑轮组利用箱子运送建材上楼,每次运送量不定。滑轮组的机械效率随重
力不同的建材变化的图象如图乙所示,滑轮与钢绳间的摩擦力及箱子和绳重忽略不计。求:
(1)若工人用300N的拉力,将建材匀速竖直向上提升了4m,工人所做功;
(2)当所运送建材的重为500N时,工人作用在绳子上的拉力;
(3)当滑轮组的机械效率为80%时,所运送建材受到的重力。
【答案】(1)拉力移动距离:s=nh=2×4m=8m,
拉力做功:W=Fs=300N×8m=2400J; (2分)
(2)由图乙可知,建材的重为500N时,滑轮组机械效率为50%,
由η====得,建材的重为500N时,工人作用在绳子上的拉力;
F==500N; (2分)
(3)由F=(G+G动)得,动滑轮重:G动=2F﹣G=2×500N﹣500N=500N,
由η====得当机械效率为80%时,所运送建材受到的重力:
G′==2000N。 (2分)
