四川省眉山市彭山区第一中学2022-2023学年高一下学期4月月考数学试题(PDF版含答案)
文档属性
| 名称 | 四川省眉山市彭山区第一中学2022-2023学年高一下学期4月月考数学试题(PDF版含答案) |

|
|
| 格式 | |||
| 文件大小 | 362.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-14 00:00:00 | ||
图片预览



文档简介
彭山一中高 25 届高一下 4月考数学试题
一、选择题:本题共 8 小题,每小题 5 分,共 40 分.在每小题给出的四个选项中,只有一
项是符合题目要求的.
1. cos2040 ( )
1
A. B. 3
1
C. D. 3
2 2 2 2
2.函数 f x 3sin x π 1的最小正周期和最大值分别是( )
4 6
π π
A. 和3 B. 和 2 C.8π和3 D.8π和 2
2 2
3.化简:OA OC OB CO ( )
A.0 B.BA C. AB D. AC
4.函数 f x tan 2x
图象的一个对称中心是( )
4
A. ,0
B. ,0
4 C.
,0 D. 0,0
4 8
5.已知角 a的终边经过点 P( 4m,3m)(m 0),则2sina cosa的值是( )
2 2 2 2
A.1或 1 B. 或 C.1或 D. 1或
5 5 5 5
6.已知函数 f x cos 2x
π
,则( )
6
A. f x π π的图象关于点 ,0 对称 B. f x 的图象关于直线 x 对称
12
12
C. f
π
x 为奇函数 D. f x 为偶函数
6
x π
7.要得到 y x sin 的图象,只需将函数 y cos 的图象( )2 2 4
π π
A.向左平移 个单位长度 B.向右平移 个单位长度
4 4
π
C.向左平移 个单位长度 D.向右平移 个单位长度
2 2
8.已知函数 f (x) sin x
( 0)在区间[0, ]上有且仅有 4条对称轴,给出下列四个结论:① f (x)
4
在区间 (0, )上有且仅有 3个不同的零点;② f (x)
的最小正周期可能是 ;
2
13 17 ③ 的取值范围是 , ;④ f (x)在区间 0, 上单调递增. 其中所有正确结论的序号是( ) 4 4 15
A.①④ B.②③ C.②④ D.②③④
二、多选题(每小题 5 分,全部选项选对得 5 分,部分选对得 2 分,有选错的得 0 分,共 20 分)
9. 下列命题正确的是( )
A.零向量与任意向量平行 B. a b 是向量a b的必要不充分条件
C.向量 AB与向量CD是共线向量,则点 A,B,C,D必在同一条直线上
D.若 a//b,b//c,则 a//c
10. 下列三角式中,值为 1的是( )
A. 4sin15 cos15 2 cos2B. sin
2 2 tan 22.5 1 1
C. D. cos
6 6 1 tan2 22.5 2 2 6
11. 已知函数 f x 2sin2 x sin 2x 1,则( )
A. f x 的图象可由 y 2 sin 2x的图象向右平移 个单位长度得到
8
B. f x 在 0, 上单调递增 C. f x 在 0, 内有 2个零点
8
D. f x 在 , 0 上的最大值为 1 2
12. 已知函数 f x cos2x asin x,a R,则( )
π
A. f x 的最小正周期为 π B. f x 的图象关于直线 x 轴对称
2
π
C. 当a 2则函数 f x 在 x , π 上单调递增
6 3
D. 当 a 1时, x π , π 7 6 , f x 最小值为 0,则 , π 2 6
三、填空题:本题共 4 小题,每小题 5 分,共 20 分.
π
13.已知 sin 2cos ,则 tan
___________.
4
14. 函数 y 2 sin2 x cos x的最小值是_____________.
3
15 5 10.若 sin 2 , sin ,且 [
, ], , ,则 的值是_________.5 10 4 2 2
7π 4π
16.已知函数 f x 2cos( x )的部分图像如图所示,满足条件 f (x) f f (x) f 0
4 3
的最小正整数 x=___________
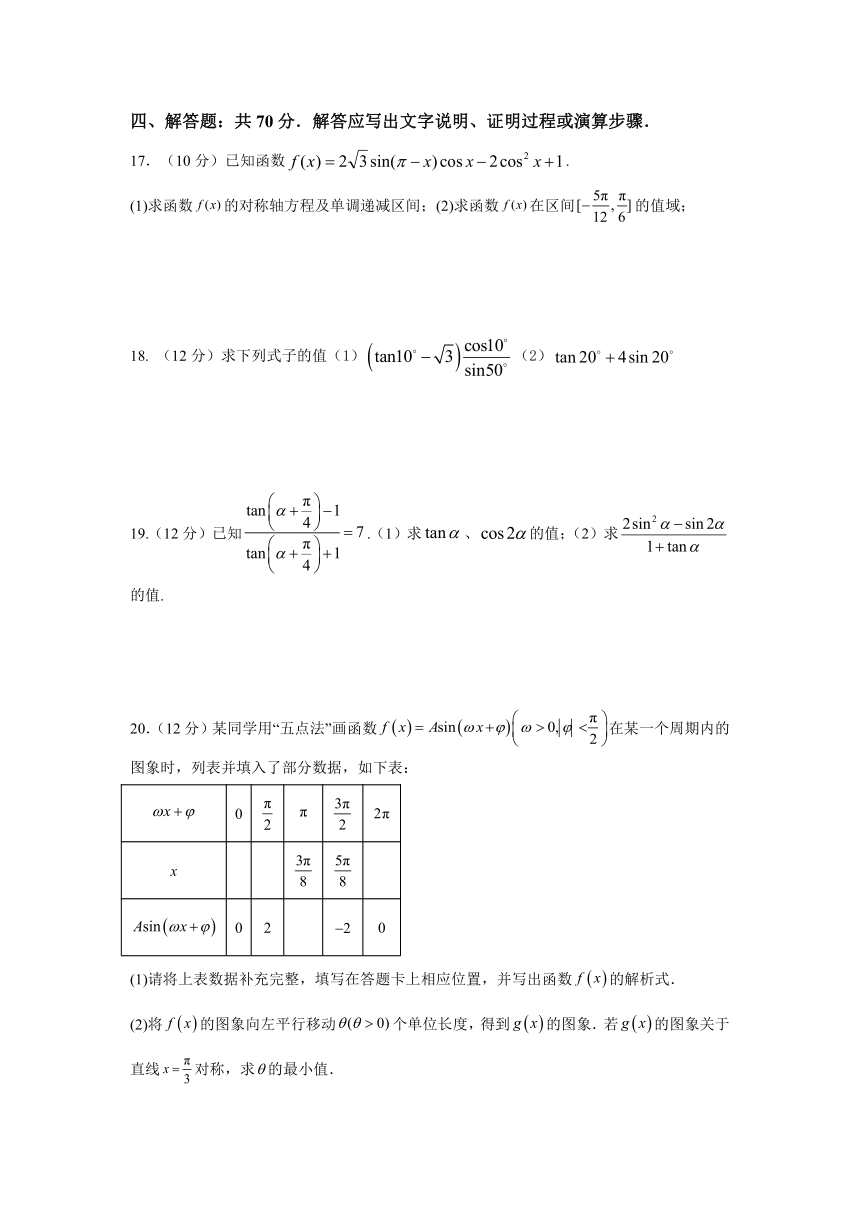
四、解答题:共 70 分.解答应写出文字说明、证明过程或演算步骤.
17.(10分)已知函数 f (x) 2 3 sin( x) cos x 2cos2 x 1 .
(1)求函数 f (x)
5π π
的对称轴方程及单调递减区间;(2)求函数 f (x)在区间[ , ]的值域;
12 6
18. (12 cos10分)求下列式子的值(1) tan10 3 (2) tan 20 4sin 20 sin50
tan π 1
4 19. 12
2
7 . 1 tan cos2 2sin sin 2 ( 分)已知 π ( )求 、 的值;(2)求tan 1 1 tan
4
的值.
20.(12分)某同学用“五点法”画函数 f x Asin x π 0,
在某一个周期内的
2
图象时,列表并填入了部分数据,如下表:
x π π 3π0 2π
2 2
3π 5π
x
8 8
Asin x 0 2 2 0
(1)请将上表数据补充完整,填写在答题卡上相应位置,并写出函数 f x 的解析式.
(2)将 f x 的图象向左平行移动 ( 0)个单位长度,得到 g x 的图象.若 g x 的图象关于
x π直线 对称,求 的最小值.
3
21.(12分)如图,已知OPQ是半径为 1,圆心角为 的扇形,点A在弧 PQ上(异于点 P,Q ),
3
过点A作 AB OP, AC OQ,垂足分别为 B,C,记 AOB ,四边形 ACOB的周长为 l .
(1)求 l关于 的函数关系式;(2)当 为何值时, l有最大值,并求出 l的最大值.
π
22.(12分)已知函数 f x Asin x A 0, 0, 的部分图像如图所示.
2
(1)求函数 y f x 的解析式;
π
(2)将 y f x 1的图像上所有点的横坐标缩短到原来的 2 ,纵坐标不变,再向右平移 个单6
位长度得到 y g x 的图像,求函数 g x 的解析式与单调递增区间;
π π π π
(3)在第(2)问的前提下,对于任意 x1 , ,是否总存在实数 x2 , ,使得 3 3 6 6
f x1 g x2 m成立 若存在,求出实数m的值或取值范围;若不存在,说明理由.
彭山一中高 25 届高一下 4 月考数学试题 参考答案
1----4 ADBC 5----8 BCDB 9 . AB 10. ABC 11. BCD 12. BD
1
7 3
13. 3 14. 15. 4 16.2
4
3 1 π
17.(1) f (x) 3sin2x cos2x 2 sin2x cos2x
2 2
2sin 2x ,
6
令 2x k ,则对称轴为 x k , k Z
6 2 3 2
2k 2x 3 令 2k 5 , k Z,则 k x k , k Z,
2 6 2 3 6
5
所以单调递减区间为[ k , k ], k Z .(写成开区间也可以)
3 6
5π π π 1
(2)∵ x [ , ],则 2x
π π
[ π, ] ,∴ 1 sin 2x ,12 6 6 6 6 2
∴ 2 2sin
2x π
5π π
1,故函数 f x 在区间[ , ]的值域为[ 2,1] .
6 12 6
sin10 cos10 sin10 3 cos10 cos10
18(1)原式= (
cos10
3) = ( )
sin 50 cos10 sin 50
2sin(10 60 ) cos10
= =-2cos10 sin 50
tan 20 4sin 20 sin 20
4sin 20 cos 20 sin 20 2sin 40
(2) cos 20
cos 20
= sin 20
2sin(60 20 ) sin 20 2sin 60 cos20 2cos60 sin 20
3
cos20 cos20
19.【小问 1 详解】
cos 2
tan 4
解法一:由已知得 ,则 tan 7
10
,若 为第一象限角,则 ,
4 3
sin
7 2
10
cos
2
10 2 2 24若 为第三象限角,则 ,故 cos 2 cos sin .
sin 7 2 25 10
1
tan π 4解法二:由已知得 ,则 tan 7,则
4 3
2
cos2 cos2 sin2 1 tan 24 .
1 tan2 25
【小问 2 详解】
49 7 2
解法一:由(1)知 tan 7,则 sin2 , sin 2 2sin sin 2 21,故 .
50 25 1 tan 100
解法二:由已知得 tan 7,则
2sin2 sin 2 2sin2 2sin cos 2 tan2 2 tan 21
1 tan 1 tan sin2 cos2 1 tan tan2 1 100 .
20.(1)根据表中已知数据,得 A 2,
T 4 5π 3π π,可得 2,
8 8
3π
当 x 时, x π,解得
π
,
8 4
f x 2sin 2x π 所以 .
4
数据补全如下表:
x π 3π0 π 2π
2 2
π π 3π 5π 7π
x
8 8 8 8 8
Asin x 0 2 0 2 0
(2)由(1)知 f x 2sin 2x
π
,得 g x 2sin
2x 2
π
.
4 4
令 2x 2
π π
kπ,解得 x
kπ π
, k Z .
4 2 2 8
π
由于函数 g x 的图象关于直线 x 对称,
3
kπ π π
令
kπ 5π
,解得 , k Z .
2 8 3 2 24
7π
由 0可知,当 k 1时, 取得最小值 .
24
2
21.(1) AB OA sin sin ,OB OA cos cos
AC OA sin sin
,OC OA cos
cos
3 3 3 3
l sin cos sin cos
3 3
sin cos 3 cos 1 sin 1 3 cos sin
2 2 2 2
1 3
sin 3 3 cos 3 1 sin 3cos 3 1 sin 3 0 2 2 2 3
2
(2)0 , , sin
,当 时, 1, l 3 13 3 3 3 3 2 6 3 max
所以 时, l
6 max
3 1.
T 7π π π 2π
22.(1)由图可知 A 1, ,则T π , 2,
4 12 3 4
所以 f x sin 2x , f 7π 7π sin
1 .
12 6
7π π 5π
所以 2kπ(k Z),即 2kπ(k Z)
6 2 3
π
又
π
,所以当 k 1 π 时, ,所以 f x sin 2x 2 3 . 3
(2)将 y f x 1的图像上所有点的横坐标缩短到原来的 2 ,纵坐标不变,
π
得: y sin
4x
π
,再向右平移 个单位长度得到:
3 6
g x sin 4 x π π sin
4x
π
π ,由 2kπ 4x
π π
2kπ, k Z ,
6 3 3 2 3 2
π kπ x 5π kπ解得 , k Z ,所以函数 g x 的单调递增区间为
24 2 24 2
π kπ , 5π kπ
k Z 24 2 24 2
(3)由 f x1 g x2 m,得 g x2 m f x1 ,
π x π π 2x π π 3 由 1 ,得 1 ,所以 sin
3 3 3 3 2
2x1 3
1,
m f x 3
π π π π
所以 1 m 1, m .又 x2 ,得 π 4x2 ,
2 6 6 3 3
1 sin 4x π 3所以 2 .
3 2
3
3 3
由题可知 m 1,m 2
1, ,
2
m 1 1
得 3 3,解得m 0,所以存在m 0,
m 2 2
使得 f x1 g x2 m成立.
4
一、选择题:本题共 8 小题,每小题 5 分,共 40 分.在每小题给出的四个选项中,只有一
项是符合题目要求的.
1. cos2040 ( )
1
A. B. 3
1
C. D. 3
2 2 2 2
2.函数 f x 3sin x π 1的最小正周期和最大值分别是( )
4 6
π π
A. 和3 B. 和 2 C.8π和3 D.8π和 2
2 2
3.化简:OA OC OB CO ( )
A.0 B.BA C. AB D. AC
4.函数 f x tan 2x
图象的一个对称中心是( )
4
A. ,0
B. ,0
4 C.
,0 D. 0,0
4 8
5.已知角 a的终边经过点 P( 4m,3m)(m 0),则2sina cosa的值是( )
2 2 2 2
A.1或 1 B. 或 C.1或 D. 1或
5 5 5 5
6.已知函数 f x cos 2x
π
,则( )
6
A. f x π π的图象关于点 ,0 对称 B. f x 的图象关于直线 x 对称
12
12
C. f
π
x 为奇函数 D. f x 为偶函数
6
x π
7.要得到 y x sin 的图象,只需将函数 y cos 的图象( )2 2 4
π π
A.向左平移 个单位长度 B.向右平移 个单位长度
4 4
π
C.向左平移 个单位长度 D.向右平移 个单位长度
2 2
8.已知函数 f (x) sin x
( 0)在区间[0, ]上有且仅有 4条对称轴,给出下列四个结论:① f (x)
4
在区间 (0, )上有且仅有 3个不同的零点;② f (x)
的最小正周期可能是 ;
2
13 17 ③ 的取值范围是 , ;④ f (x)在区间 0, 上单调递增. 其中所有正确结论的序号是( ) 4 4 15
A.①④ B.②③ C.②④ D.②③④
二、多选题(每小题 5 分,全部选项选对得 5 分,部分选对得 2 分,有选错的得 0 分,共 20 分)
9. 下列命题正确的是( )
A.零向量与任意向量平行 B. a b 是向量a b的必要不充分条件
C.向量 AB与向量CD是共线向量,则点 A,B,C,D必在同一条直线上
D.若 a//b,b//c,则 a//c
10. 下列三角式中,值为 1的是( )
A. 4sin15 cos15 2 cos2B. sin
2 2 tan 22.5 1 1
C. D. cos
6 6 1 tan2 22.5 2 2 6
11. 已知函数 f x 2sin2 x sin 2x 1,则( )
A. f x 的图象可由 y 2 sin 2x的图象向右平移 个单位长度得到
8
B. f x 在 0, 上单调递增 C. f x 在 0, 内有 2个零点
8
D. f x 在 , 0 上的最大值为 1 2
12. 已知函数 f x cos2x asin x,a R,则( )
π
A. f x 的最小正周期为 π B. f x 的图象关于直线 x 轴对称
2
π
C. 当a 2则函数 f x 在 x , π 上单调递增
6 3
D. 当 a 1时, x π , π 7 6 , f x 最小值为 0,则 , π 2 6
三、填空题:本题共 4 小题,每小题 5 分,共 20 分.
π
13.已知 sin 2cos ,则 tan
___________.
4
14. 函数 y 2 sin2 x cos x的最小值是_____________.
3
15 5 10.若 sin 2 , sin ,且 [
, ], , ,则 的值是_________.5 10 4 2 2
7π 4π
16.已知函数 f x 2cos( x )的部分图像如图所示,满足条件 f (x) f f (x) f 0
4 3
的最小正整数 x=___________
四、解答题:共 70 分.解答应写出文字说明、证明过程或演算步骤.
17.(10分)已知函数 f (x) 2 3 sin( x) cos x 2cos2 x 1 .
(1)求函数 f (x)
5π π
的对称轴方程及单调递减区间;(2)求函数 f (x)在区间[ , ]的值域;
12 6
18. (12 cos10分)求下列式子的值(1) tan10 3 (2) tan 20 4sin 20 sin50
tan π 1
4 19. 12
2
7 . 1 tan cos2 2sin sin 2 ( 分)已知 π ( )求 、 的值;(2)求tan 1 1 tan
4
的值.
20.(12分)某同学用“五点法”画函数 f x Asin x π 0,
在某一个周期内的
2
图象时,列表并填入了部分数据,如下表:
x π π 3π0 2π
2 2
3π 5π
x
8 8
Asin x 0 2 2 0
(1)请将上表数据补充完整,填写在答题卡上相应位置,并写出函数 f x 的解析式.
(2)将 f x 的图象向左平行移动 ( 0)个单位长度,得到 g x 的图象.若 g x 的图象关于
x π直线 对称,求 的最小值.
3
21.(12分)如图,已知OPQ是半径为 1,圆心角为 的扇形,点A在弧 PQ上(异于点 P,Q ),
3
过点A作 AB OP, AC OQ,垂足分别为 B,C,记 AOB ,四边形 ACOB的周长为 l .
(1)求 l关于 的函数关系式;(2)当 为何值时, l有最大值,并求出 l的最大值.
π
22.(12分)已知函数 f x Asin x A 0, 0, 的部分图像如图所示.
2
(1)求函数 y f x 的解析式;
π
(2)将 y f x 1的图像上所有点的横坐标缩短到原来的 2 ,纵坐标不变,再向右平移 个单6
位长度得到 y g x 的图像,求函数 g x 的解析式与单调递增区间;
π π π π
(3)在第(2)问的前提下,对于任意 x1 , ,是否总存在实数 x2 , ,使得 3 3 6 6
f x1 g x2 m成立 若存在,求出实数m的值或取值范围;若不存在,说明理由.
彭山一中高 25 届高一下 4 月考数学试题 参考答案
1----4 ADBC 5----8 BCDB 9 . AB 10. ABC 11. BCD 12. BD
1
7 3
13. 3 14. 15. 4 16.2
4
3 1 π
17.(1) f (x) 3sin2x cos2x 2 sin2x cos2x
2 2
2sin 2x ,
6
令 2x k ,则对称轴为 x k , k Z
6 2 3 2
2k 2x 3 令 2k 5 , k Z,则 k x k , k Z,
2 6 2 3 6
5
所以单调递减区间为[ k , k ], k Z .(写成开区间也可以)
3 6
5π π π 1
(2)∵ x [ , ],则 2x
π π
[ π, ] ,∴ 1 sin 2x ,12 6 6 6 6 2
∴ 2 2sin
2x π
5π π
1,故函数 f x 在区间[ , ]的值域为[ 2,1] .
6 12 6
sin10 cos10 sin10 3 cos10 cos10
18(1)原式= (
cos10
3) = ( )
sin 50 cos10 sin 50
2sin(10 60 ) cos10
= =-2cos10 sin 50
tan 20 4sin 20 sin 20
4sin 20 cos 20 sin 20 2sin 40
(2) cos 20
cos 20
= sin 20
2sin(60 20 ) sin 20 2sin 60 cos20 2cos60 sin 20
3
cos20 cos20
19.【小问 1 详解】
cos 2
tan 4
解法一:由已知得 ,则 tan 7
10
,若 为第一象限角,则 ,
4 3
sin
7 2
10
cos
2
10 2 2 24若 为第三象限角,则 ,故 cos 2 cos sin .
sin 7 2 25 10
1
tan π 4解法二:由已知得 ,则 tan 7,则
4 3
2
cos2 cos2 sin2 1 tan 24 .
1 tan2 25
【小问 2 详解】
49 7 2
解法一:由(1)知 tan 7,则 sin2 , sin 2 2sin sin 2 21,故 .
50 25 1 tan 100
解法二:由已知得 tan 7,则
2sin2 sin 2 2sin2 2sin cos 2 tan2 2 tan 21
1 tan 1 tan sin2 cos2 1 tan tan2 1 100 .
20.(1)根据表中已知数据,得 A 2,
T 4 5π 3π π,可得 2,
8 8
3π
当 x 时, x π,解得
π
,
8 4
f x 2sin 2x π 所以 .
4
数据补全如下表:
x π 3π0 π 2π
2 2
π π 3π 5π 7π
x
8 8 8 8 8
Asin x 0 2 0 2 0
(2)由(1)知 f x 2sin 2x
π
,得 g x 2sin
2x 2
π
.
4 4
令 2x 2
π π
kπ,解得 x
kπ π
, k Z .
4 2 2 8
π
由于函数 g x 的图象关于直线 x 对称,
3
kπ π π
令
kπ 5π
,解得 , k Z .
2 8 3 2 24
7π
由 0可知,当 k 1时, 取得最小值 .
24
2
21.(1) AB OA sin sin ,OB OA cos cos
AC OA sin sin
,OC OA cos
cos
3 3 3 3
l sin cos sin cos
3 3
sin cos 3 cos 1 sin 1 3 cos sin
2 2 2 2
1 3
sin 3 3 cos 3 1 sin 3cos 3 1 sin 3 0 2 2 2 3
2
(2)0 , , sin
,当 时, 1, l 3 13 3 3 3 3 2 6 3 max
所以 时, l
6 max
3 1.
T 7π π π 2π
22.(1)由图可知 A 1, ,则T π , 2,
4 12 3 4
所以 f x sin 2x , f 7π 7π sin
1 .
12 6
7π π 5π
所以 2kπ(k Z),即 2kπ(k Z)
6 2 3
π
又
π
,所以当 k 1 π 时, ,所以 f x sin 2x 2 3 . 3
(2)将 y f x 1的图像上所有点的横坐标缩短到原来的 2 ,纵坐标不变,
π
得: y sin
4x
π
,再向右平移 个单位长度得到:
3 6
g x sin 4 x π π sin
4x
π
π ,由 2kπ 4x
π π
2kπ, k Z ,
6 3 3 2 3 2
π kπ x 5π kπ解得 , k Z ,所以函数 g x 的单调递增区间为
24 2 24 2
π kπ , 5π kπ
k Z 24 2 24 2
(3)由 f x1 g x2 m,得 g x2 m f x1 ,
π x π π 2x π π 3 由 1 ,得 1 ,所以 sin
3 3 3 3 2
2x1 3
1,
m f x 3
π π π π
所以 1 m 1, m .又 x2 ,得 π 4x2 ,
2 6 6 3 3
1 sin 4x π 3所以 2 .
3 2
3
3 3
由题可知 m 1,m 2
1, ,
2
m 1 1
得 3 3,解得m 0,所以存在m 0,
m 2 2
使得 f x1 g x2 m成立.
4
同课章节目录
