三角形的外角和[上学期]
图片预览


文档简介
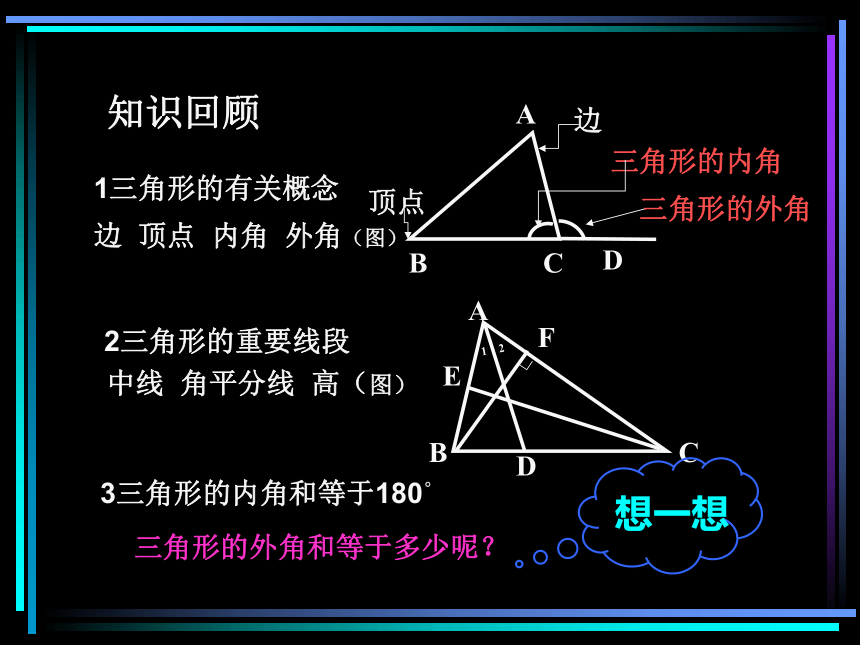
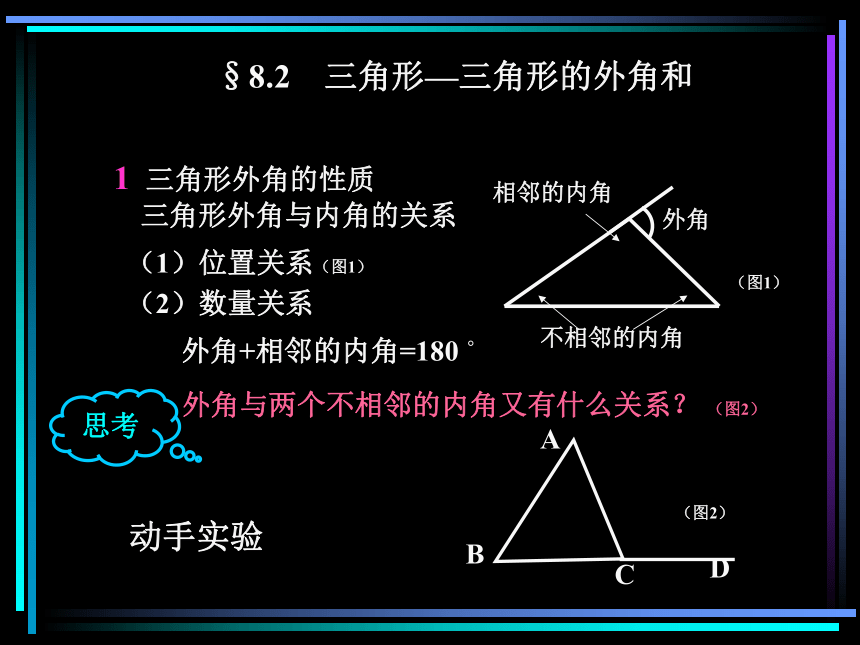
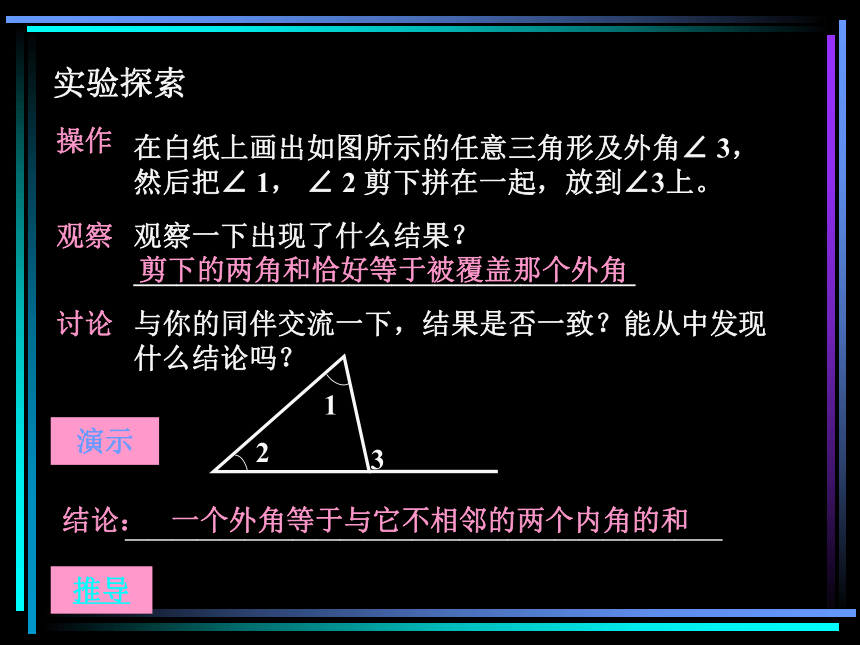
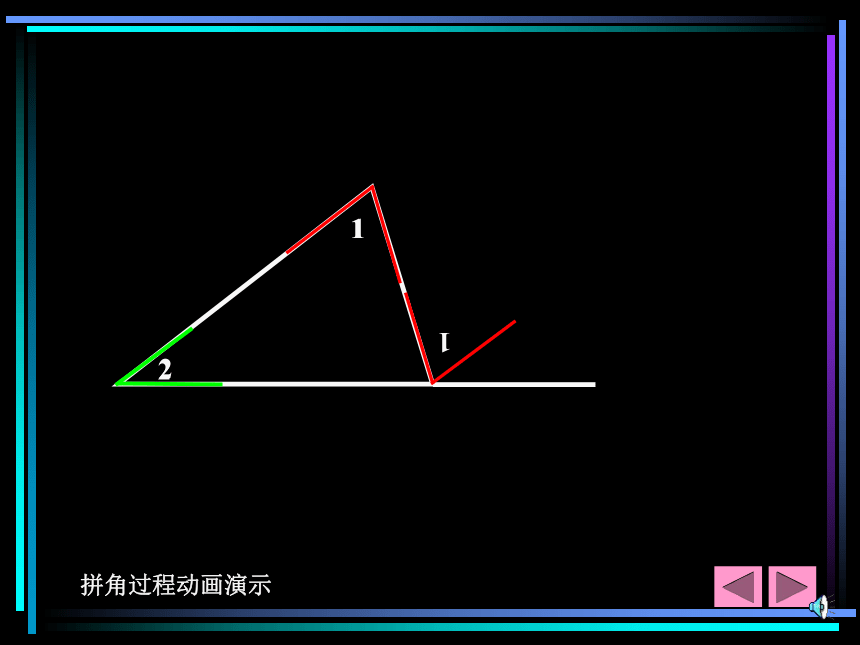
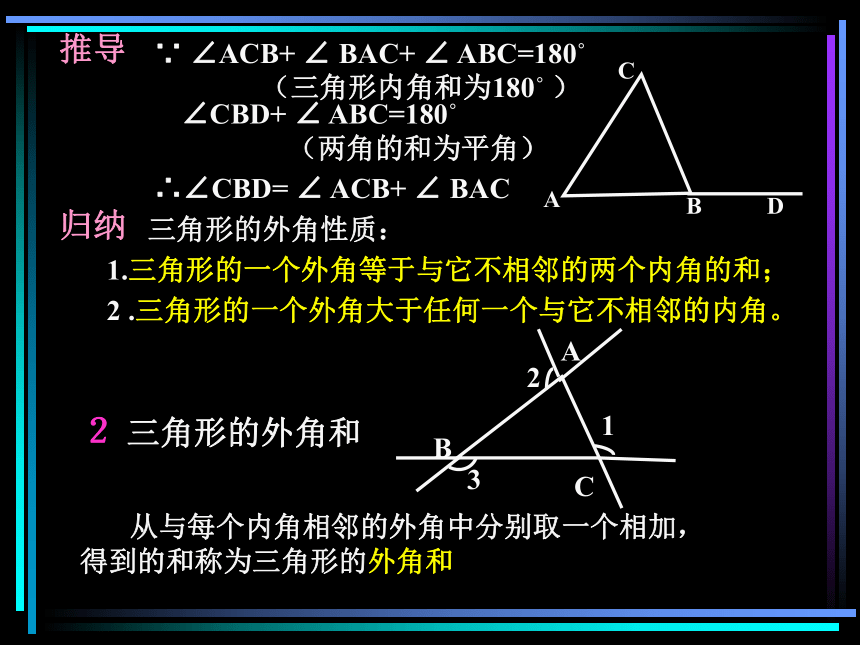
课件26张PPT。初一数学演示文稿课堂小结知识回顾动手实验结论总结举例说明学生练习三角形的外角和知识回顾1三角形的有关概念边 顶点 内角 外角(图)2三角形的重要线段中线 角平分线 高(图)3三角形的内角和等于180?BCD顶点边三角形的内角AEDF1 2§8.2 三角形—三角形的外角和外角相邻的内角不相邻的内角1 三角形外角的性质三角形外角与内角的关系(1)位置关系(图1)(2)数量关系外角+相邻的内角=180 ?外角与两个不相邻的内角又有什么关系? (图2)动手实验(图1)(图2)思考操作观察讨论在白纸上画出如图所示的任意三角形及外角∠ 3,然后把∠ 1, ∠ 2 剪下拼在一起,放到∠3上。观察一下出现了什么结果?___________________________________与你的同伴交流一下,结果是否一致?能从中发现什么结论吗? 剪下的两角和恰好等于被覆盖那个外角一个外角等于与它不相邻的两个内角的和2演示推导13实验探索拼角过程动画演示12推导 归纳1.三角形的一个外角等于与它不相邻的两个内角的和;2 .三角形的一个外角大于任何一个与它不相邻的内角。2 三角形的外角和 从与每个内角相邻的外角中分别取一个相加,得到的和称为三角形的外角和∵ ∠ACB+ ∠ BAC+ ∠ ABC=180?
(三角形内角和为180? )∠CBD+ ∠ ABC=180?
(两角的和为平角)∴∠CBD= ∠ ACB+ ∠ BAC三角形的外角性质:ABC推导 归纳1.三角形的一个外角等于与它不相邻的两个内角的和;2 .三角形的一个外角大于任何一个与它不相邻的内角。2 三角形的外角和 从与每个内角相邻的外角中分别取一个相加,得到的和称为三角形的外角和∵ ∠ACB+ ∠ BAC+ ∠ ABC=180?
(三角形内角和为180? )∠CBD+ ∠ ABC=180?
(两角的和为平角)∴∠CBD= ∠ ACB+ ∠ BAC三角形的外角性质:ABC∠1 + =180?
∠ 2 + =180?
∠ 3 + =180?三式相加可得
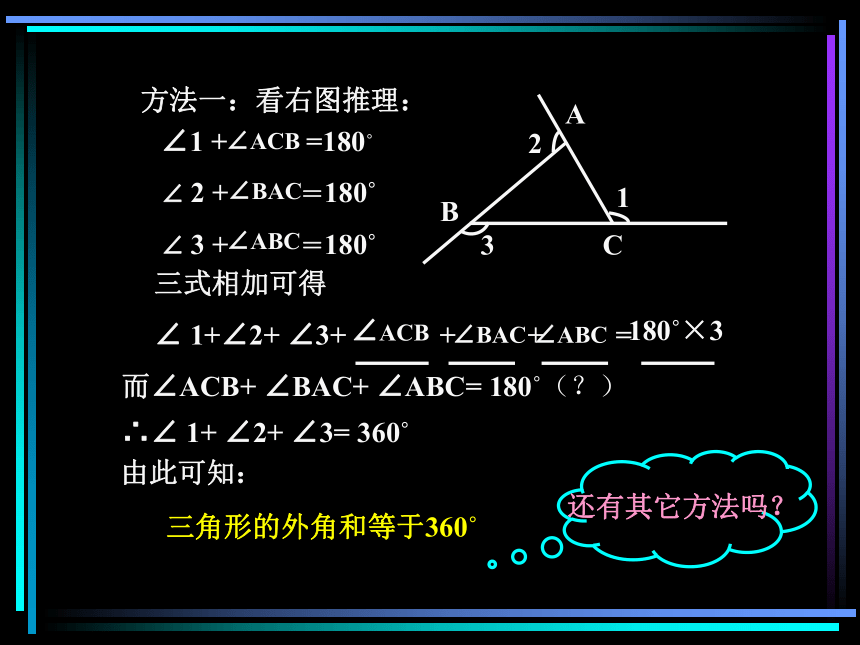
∠ 1+∠2+ ∠3+ + + = 而∠ACB+ ∠BAC+ ∠ABC= 180?(?)∴∠ 1+ ∠2+ ∠3= 360?方法一:看右图推理:由此可知:三角形的外角和等于360?∠ACB∠BAC∠ABC180?×3∠ACB∠BAC∠ABC还有其它方法吗?CE方法二:在图中,过点A作 AD‖BC,请试用本图
来说明∠ 1+ ∠2+ ∠3的值. 推导:∵ AD‖BC (已知)∴∠1 = ∠EAD
∠3 = ∠DAB (两直线平行,同位角相等)∴ ∠1 + ∠2 + ∠3
=∠EAD+ ∠2 + ∠DAB
=360?三角形的外角和等于360 ?补充方法12补充方法2例1 如图,D是△ABC的边BC上一点, ∠B=∠BAD, ∠ADC=80 ? , ∠BAC=70?. 求:解答(1)∵ ∠ADC是ABD的外角∴∠B+∠BAD=∠ADC=80?
(三角形的一 个外角等于与它不相邻的两个内角的和)又∵ ∠B=∠BAD∴∠B=40 ? (2)∵在ABC中 ∠ B+ ∠ BAC+ ∠ C= 180 ? ∴∠ C= 180 ? - ∠ B - ∠ BAC= 180 ? -40 ? -70 ?
=70 ?(三角形的内角和为180 ? )(1) ∠ B的度数;(2) ∠ C的度数。ABDC80 ?如图五角星中:∠A+∠B+∠C+∠D+∠E= ——180?解答:例2∵∠AMN是△MCE 的外角∴∠AMN =∠C+∠E (三角形的
一 个外角等于与它不相邻的个内角的和)同理 : ∠ ANM= ∠ B+ ∠ D∴ ∠ A+ ∠ B+ ∠ C+ ∠ D+ ∠ E= ∠ A+( ∠ B+ ∠ D)+( ∠ C+ ∠ E)= ∠ A+ ∠ AMN + ∠ ANM =180 ?例 3 三角形的三个外角之比为2:3:4,
则与它们相邻的内角分别为( )A. 80? 120? 160 ? B. 160 ? 120 ? 80 ?
C. 100 ? 60 ? 20 ? D. 140 ? 120 ? 100 ? 解 设三角形的三个外角分别为2k,3k,4k,根据三角形的外角和等于360 ? ,有
2k+3k+4k= 360 ? , 可解得k=40 ?,三个外角分别为80? 120? 160 ? , 则相邻的内角分
别为100 ? 60 ? 20 ? 故选 CC练习⒈ (口答)一个三角形可以有两个内角都是直角吗?可以有两个内角都是钝角或都是锐角吗?为什么?2.求出下列各图中∠1的度数. 30°60 °35 °120 °1145 °50 °1∠1=——∠1=——∠1=——90 °85 °95 °3 如图,飞机要从A地飞往B地,因受大风影响, 一开始就偏离航线(AB)18?(即∠A=18?)飞到了C地,已知∠ABC=10?,问飞机现在应以怎样角度飞行才能到达B处?(即求∠BCD的度数____)ACDB28 ?18°?4. 如图,在直角ΔABC中,CD是斜边AB上的高, ∠BCD=35 ? ,求∠A与∠EBC的度数.∠ A= 35 ?再练∠EBC=125 ?4. 如图,在直角ΔABC中,CD是斜边AB上的高, ∠BCD=35 ? ,求∠A与∠EBC的度数.解答∵直角ΔABC中,∠ ACB=90°
∴ ∠ AC D=90 ?- ∠ BCD=90 ?-35 ?=55° ∵ CD是高, ∴ ∠ BDC=90°
∵ ∠ BCD= ∠ A+ ∠ ACD
(三角形的一个外角等于与它不相邻
的个内角的和) ∴ ∠ A= ∠ BCD- ∠ ACD=90 ?-55 ?=35 ?
∴ ∠ EBC= ∠ A+ ∠ BCA (三角形的
一 个外角等于与它不相邻的个内角的和)
=35 ?+90 ?=125 ?再练课堂小结1 三角形的外角性质: 三角形的一个外角等于与它不相邻的两个内角的和;三角形的一个外角大于任何一个与它不相邻的内角。2 三角形的内角和等于180?三角形的外角和等于360 ?3 在求角的度数时,常可利用三角形的内角和及外角的性质来找数量关系;涉及图形时,可先把已知条件尽可能的在图中标出来,有助于直观分析题意。作业布置:P52 3,4。THE END策划
设计郁锦裕Email: yujy @ mdez.net
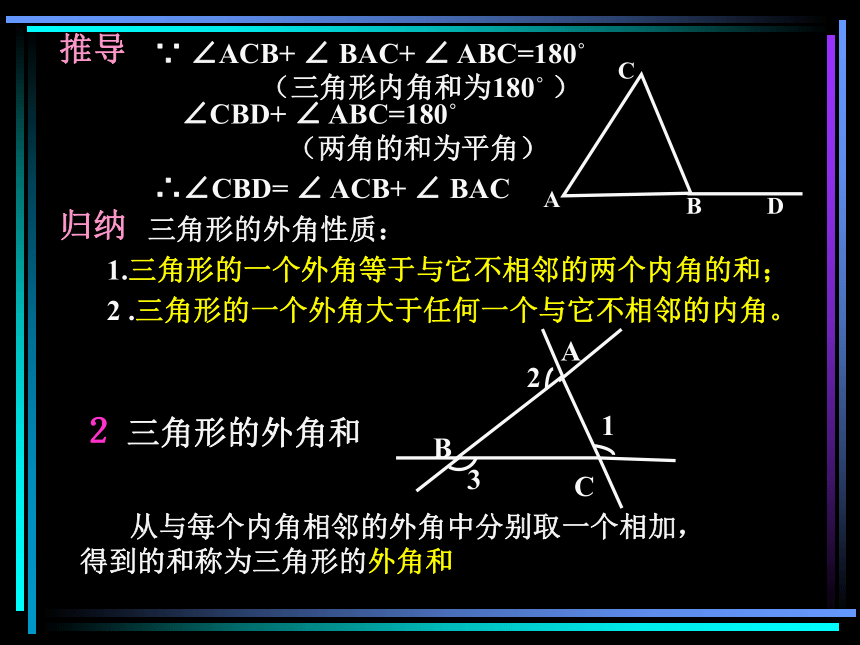
(三角形内角和为180? )∠CBD+ ∠ ABC=180?
(两角的和为平角)∴∠CBD= ∠ ACB+ ∠ BAC三角形的外角性质:ABC推导 归纳1.三角形的一个外角等于与它不相邻的两个内角的和;2 .三角形的一个外角大于任何一个与它不相邻的内角。2 三角形的外角和 从与每个内角相邻的外角中分别取一个相加,得到的和称为三角形的外角和∵ ∠ACB+ ∠ BAC+ ∠ ABC=180?
(三角形内角和为180? )∠CBD+ ∠ ABC=180?
(两角的和为平角)∴∠CBD= ∠ ACB+ ∠ BAC三角形的外角性质:ABC∠1 + =180?
∠ 2 + =180?
∠ 3 + =180?三式相加可得
∠ 1+∠2+ ∠3+ + + = 而∠ACB+ ∠BAC+ ∠ABC= 180?(?)∴∠ 1+ ∠2+ ∠3= 360?方法一:看右图推理:由此可知:三角形的外角和等于360?∠ACB∠BAC∠ABC180?×3∠ACB∠BAC∠ABC还有其它方法吗?CE方法二:在图中,过点A作 AD‖BC,请试用本图
来说明∠ 1+ ∠2+ ∠3的值. 推导:∵ AD‖BC (已知)∴∠1 = ∠EAD
∠3 = ∠DAB (两直线平行,同位角相等)∴ ∠1 + ∠2 + ∠3
=∠EAD+ ∠2 + ∠DAB
=360?三角形的外角和等于360 ?补充方法12补充方法2例1 如图,D是△ABC的边BC上一点, ∠B=∠BAD, ∠ADC=80 ? , ∠BAC=70?. 求:解答(1)∵ ∠ADC是ABD的外角∴∠B+∠BAD=∠ADC=80?
(三角形的一 个外角等于与它不相邻的两个内角的和)又∵ ∠B=∠BAD∴∠B=40 ? (2)∵在ABC中 ∠ B+ ∠ BAC+ ∠ C= 180 ? ∴∠ C= 180 ? - ∠ B - ∠ BAC= 180 ? -40 ? -70 ?
=70 ?(三角形的内角和为180 ? )(1) ∠ B的度数;(2) ∠ C的度数。ABDC80 ?如图五角星中:∠A+∠B+∠C+∠D+∠E= ——180?解答:例2∵∠AMN是△MCE 的外角∴∠AMN =∠C+∠E (三角形的
一 个外角等于与它不相邻的个内角的和)同理 : ∠ ANM= ∠ B+ ∠ D∴ ∠ A+ ∠ B+ ∠ C+ ∠ D+ ∠ E= ∠ A+( ∠ B+ ∠ D)+( ∠ C+ ∠ E)= ∠ A+ ∠ AMN + ∠ ANM =180 ?例 3 三角形的三个外角之比为2:3:4,
则与它们相邻的内角分别为( )A. 80? 120? 160 ? B. 160 ? 120 ? 80 ?
C. 100 ? 60 ? 20 ? D. 140 ? 120 ? 100 ? 解 设三角形的三个外角分别为2k,3k,4k,根据三角形的外角和等于360 ? ,有
2k+3k+4k= 360 ? , 可解得k=40 ?,三个外角分别为80? 120? 160 ? , 则相邻的内角分
别为100 ? 60 ? 20 ? 故选 CC练习⒈ (口答)一个三角形可以有两个内角都是直角吗?可以有两个内角都是钝角或都是锐角吗?为什么?2.求出下列各图中∠1的度数. 30°60 °35 °120 °1145 °50 °1∠1=——∠1=——∠1=——90 °85 °95 °3 如图,飞机要从A地飞往B地,因受大风影响, 一开始就偏离航线(AB)18?(即∠A=18?)飞到了C地,已知∠ABC=10?,问飞机现在应以怎样角度飞行才能到达B处?(即求∠BCD的度数____)ACDB28 ?18°?4. 如图,在直角ΔABC中,CD是斜边AB上的高, ∠BCD=35 ? ,求∠A与∠EBC的度数.∠ A= 35 ?再练∠EBC=125 ?4. 如图,在直角ΔABC中,CD是斜边AB上的高, ∠BCD=35 ? ,求∠A与∠EBC的度数.解答∵直角ΔABC中,∠ ACB=90°
∴ ∠ AC D=90 ?- ∠ BCD=90 ?-35 ?=55° ∵ CD是高, ∴ ∠ BDC=90°
∵ ∠ BCD= ∠ A+ ∠ ACD
(三角形的一个外角等于与它不相邻
的个内角的和) ∴ ∠ A= ∠ BCD- ∠ ACD=90 ?-55 ?=35 ?
∴ ∠ EBC= ∠ A+ ∠ BCA (三角形的
一 个外角等于与它不相邻的个内角的和)
=35 ?+90 ?=125 ?再练课堂小结1 三角形的外角性质: 三角形的一个外角等于与它不相邻的两个内角的和;三角形的一个外角大于任何一个与它不相邻的内角。2 三角形的内角和等于180?三角形的外角和等于360 ?3 在求角的度数时,常可利用三角形的内角和及外角的性质来找数量关系;涉及图形时,可先把已知条件尽可能的在图中标出来,有助于直观分析题意。作业布置:P52 3,4。THE END策划
设计郁锦裕Email: yujy @ mdez.net
