第一单元图形的运动(二)(单元测试)五年级下册数学冀教版(含答案)
文档属性
| 名称 | 第一单元图形的运动(二)(单元测试)五年级下册数学冀教版(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 773.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-14 00:00:00 | ||
图片预览




文档简介
第一单元图形的运动(二)(单元测试)五年级下册数学(冀教版)
学校:___________姓名:___________班级:___________考号:__________
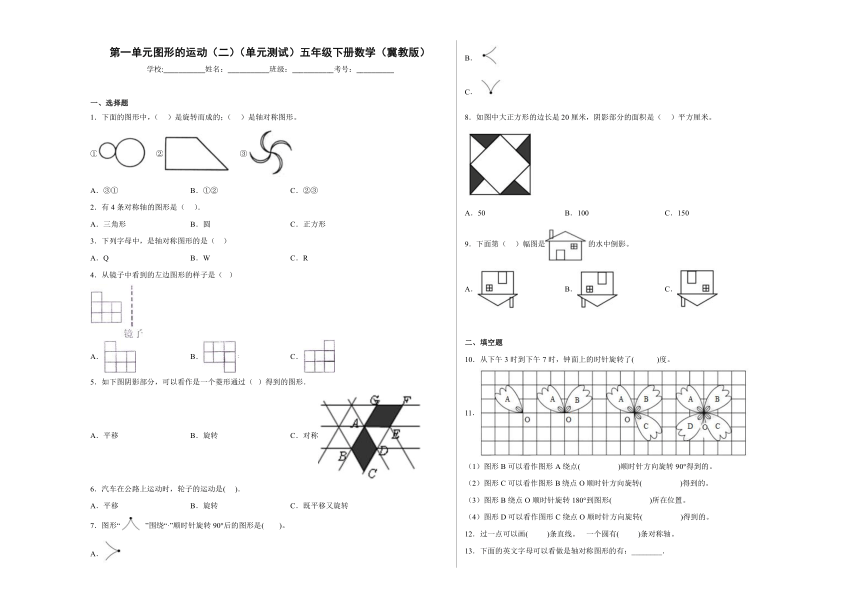
一、选择题
1.下面的图形中,( )是旋转而成的;( )是轴对称图形。
① ② ③
A.③① B.①② C.②③
2.有4条对称轴的图形是( ).
A.三角形 B.圆 C.正方形
3.下列字母中,是轴对称图形的是( )
A.Q B.W C.R
4.从镜子中看到的左边图形的样子是( )
A. B. C.
5.如下图阴影部分,可以看作是一个菱形通过( )得到的图形.
A.平移 B.旋转 C.对称
6.汽车在公路上运动时,轮子的运动是( ).
A.平移 B.旋转 C.既平移又旋转
7.图形“”围绕“·”顺时针旋转90°后的图形是( )。
A.
B.
C.
8.如图中大正方形的边长是20厘米,阴影部分的面积是( )平方厘米。
A.50 B.100 C.150
9.下面第( )幅图是的水中倒影。
A. B. C.
二、填空题
10.从下午3时到下午7时,钟面上的时针旋转了( )度。
11.
(1)图形B可以看作图形A绕点( )顺时针方向旋转90°得到的。
(2)图形C可以看作图形B绕点O顺时针方向旋转( )得到的。
(3)图形B绕点O顺时针旋转180°到图形( )所在位置。
(4)图形D可以看作图形C绕点O顺时针方向旋转( )得到的。
12.过一点可以画( )条直线。 一个圆有( )条对称轴。
13.下面的英文字母可以看做是轴对称图形的有:________.
14.钟面上,时针从数字“2”顺时针旋转到数字“5”旋转了( )度;时针从数字“4”顺时针旋转60°到数字( )。
15.平移和旋转不改变图形的( )和( ),只改变图形的位置和方向。
16.填空题
(1)升国旗时国旗的运动属于_____运动;
(2)钟摆的运动属于_____运动;
(3)在算盘上的拨珠的运动属于_____运动;
(4)电梯的运动属于_____运动;
(5)风扇叶片的运动属于_____运动;
(6)运动的火车的运动属于_____运动;
(7)光盘在电脑里的运动属于_____运动。
17.在数字0、2、3、5、8、9中,( )是轴对称的数字。
18.图形的旋转有三个要素,一是旋转的( ),二是旋转的( ),三是旋转的( )。
三、判断题
19.直角三角形绕某一点旋转后得到的图形仍然是直角三角形。( )
20.钟表上分针的运动属于平移。( )
21.一个图形平移或者旋转后只是位置变化了,而图形的形状不改变。( )
22.等腰三角形是轴对称图形。( )
23.五角星有5条对称轴。( )
24.一个长方形绕某点顺时针旋转180°和逆时针旋转180°得到图形位置完全一样。( )
25.等腰三角形、正方形、平行四边形、圆形都是轴对称图形。( )
四、解答题
26.
(1)向( )平移了( )格。
(2)画出的另一半,使它成为轴对称图形,并画出它的一条对称轴。
(3)画出向上平移5个方格后的图形。
27.将下面的平行四边形绕顶点O顺时针旋转,每次旋转90°,旋转3次.
28.在下面图中完成如下操作,并回答问题:
(1)B点的位置是(________,________),在A点的________偏________方向约________cm处。
(2)小旗子向右平移9格后的图形。
(3)小旗子绕O点顺时针方向旋转90°的图形。
29.这里的规律你知道吗?接下来该怎么排?
30.想一想,圈一圈。
(1)如图,把一张正方形纸对折,沿虚线剪,能得到一棵完整的松树的是哪一个?
(2)要想得到六边形,下列哪种剪法是正确的?
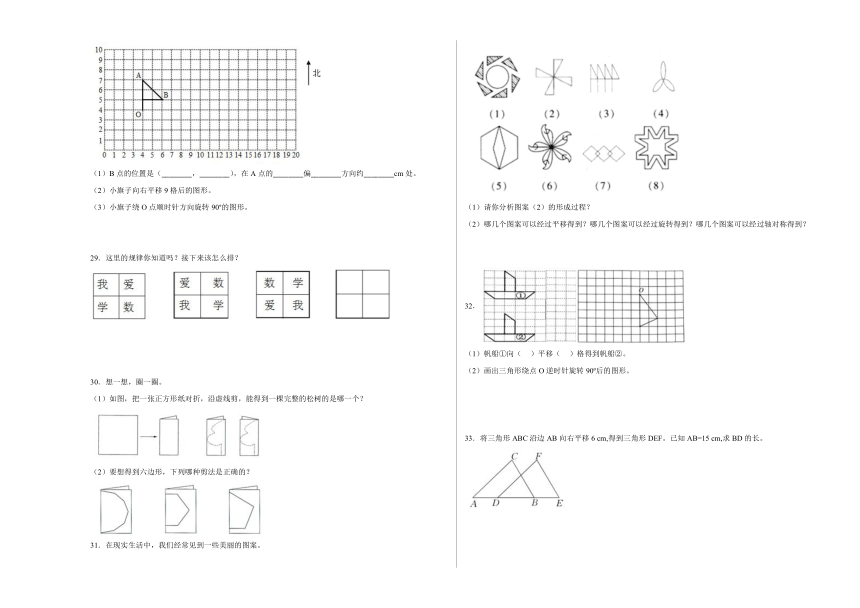
31.在现实生活中,我们经常见到一些美丽的图案。
(1)请你分析图案(2)的形成过程?
(2)哪几个图案可以经过平移得到?哪几个图案可以经过旋转得到?哪几个图案可以经过轴对称得到?
32.
(1)帆船①向( )平移( )格得到帆船②。
(2)画出三角形绕点O逆时针旋转90 后的图形。
33.将三角形ABC沿边AB向右平移6 cm,得到三角形DEF。已知AB=15 cm,求BD的长。
参考答案:
1.A
【分析】如果一个图形沿着一条直线对折后两部分完全重合,这样的图形叫做轴对称图形,这条直线叫做对称轴;如果一个图形绕某一点旋转一定的角度后能够与自身重合,那么这个图形就叫做旋转对称图形,这个点叫做旋转中心;据此对各图形分析后即可得解。
【详解】①是轴对称图形;
②不是旋转而成的图形,也不是轴对称图形;
③是旋转而成的图形;
故答案为:A。
【点睛】此题主要考查了旋转和轴对称在实际当中的运用。
2.C
3.B
4.C
【详解】根据镜面对称的特征,镜中的景物与实际景物上下前后方向一致,左右方向相反,大小不变,且关于镜面对称.镜面对称的特点是:上下前后方向一致,左右方向相反,镜中与实际景物大小不变.
从镜子中看到的左边图形的样子是 ;
故选C.
5.B
【详解】看图可知,菱形ABCD以A为中心,逆时针旋转得到菱形AEFG;据此选择即可.
6.B
7.A
8.B
【分析】如下图,把四个阴影部分的三角形平移后拼在一起,可以形成一个边长为20÷2=10厘米的小正方形,求出小正方形的面积即可解答。
【详解】20÷2=10(厘米),10×10=100(平方厘米)。
故答案为:B。
【点睛】本题主要考查学生的观察和分析能力。
9.C
【分析】要求房子的水中倒影,其实就是求房子关于水面的轴对称图形,将房子的各点相对于水面进行对称标点,然后再连接即可解答。
【详解】通过观察房子的轴对称图形可知,通过比对烟筒、窗户、门的位置即可判断出C图正确。
故答案为:C
【点睛】此题主要考查学生对轴对称图形的理解与认识,需要理解对称的定义和观察方法,需要认真仔细。
10.120
【分析】因为时钟的的圆周为360°,可以分为四份,每份90°(每90°包含了三个30°)。从下午3时走到6时,正好是90°,走到7时,也就是多了30°,90°加30°,正好是120°。
【详解】从下午3时到下午7时,用算式表达:360°÷4+30°=120°。
所以钟面上的时针旋转了120度。
【点睛】本题主要考查旋转的应用,角度的度量和钟表辨识,解答此题的关键是弄清从下午3时到晚上7时时针在钟面上运动的轨迹。
11. O 90° D 90°
【分析】决定旋转后图形的位置的要素:一是旋转中心或轴,二是旋转方向(顺时针或逆时针),三是旋转角度。
【详解】(1)图形B可以看作图形A绕点O顺时针方向旋转90°得到的;
(2)图形C可以看作图形B绕点O顺时针方向旋转90°得到的;
(3)图形B绕点O顺时针旋转180°到图形D所在位置;
(4)图形D可以看作图形C绕点O顺时针方向旋转90°得到的。
【点睛】本题考查了旋转与旋转现象,物体或图形旋转后,它们的形状、大小都不改变,只是位置发生了变化。
12. 无数 无数
13.①②③④⑦
【详解】轴对称图形是说如果一个图形沿着一条直线对折后两部分完全重合.由此可以断定以上字母可以看做轴对称图形的有①、②、③、④、⑦.
14. 90 6
【分析】钟面上,相邻两个数字间的角度是30°。先利用减法求出从“2”到“5”,时针旋转了几个数字,再乘30°,即可求出时针从数字“2”顺时针旋转到数字“5”旋转了多少度;
用60°除以30°,求出时针旋转了几个数字,再利用加法求出时针从数字“4”顺时针旋转60°到了数字几。
【详解】(5-2)×30°
=3×30°
=90°
60°÷30°+4
=2+4
=6
所以,钟面上,时针从数字“2”顺时针旋转到数字“5”旋转了90度;时针从数字“4”顺时针旋转60°到数字6。
【点睛】本题考查了旋转现象以及钟面的认识,明确钟面上相邻两个数字间的度数是解题的关键。
15. 大小 形状
【详解】平移是指在平面内,将一个图形上的所有点都按照某个方向作相同距离的移动。平移不改变图形的形状和大小,只是改变位置。把一个图形绕着某一点转动一个角度的图形变换叫做旋转,旋转时图形位置发生变化,大小不变,形状不变。所以平移和旋转不改变图形的大小和形状,只改变图形的位置和方向。
16. 平移 旋转 平移 平移 旋转 平移 旋转
【分析】根据旋转的含义,物体绕着某一点或轴运动,这种运动现象称为旋转;平移是指在平面内,将一个图形上的所有点都按照某个方向作相同距离的移动,这样的图形运动叫作图形的平移运动,据此解答。
【详解】(1)升国旗时国旗的运动属于平移运动;
(2)钟摆的运动属于旋转运动;
(3)在算盘上的拨珠的运动属于平移运动;
(4)电梯的运动属于平移运动;
(5)风扇叶片的运动属于旋转运动;
(6)运动的火车的运动属于平移运动;
(7)光盘在电脑里的运动属于旋转运动。
故答案为:(1)平移 (2)旋转 (3)平移 (4)平移 (5)旋转 (6)平移 (7)旋转
【点睛】本题考查了如何判定生活中的旋转现象和平移现象,牢记要点,旋转是绕着某个固定点旋转一定的角度,一般情况下方向会发生改变。平移是沿某一方向移动一定的距离。
17.0、3、8
【分析】如果一个平面图形沿着一条直线折叠后,直线两旁的部分能够互相重合,那么这个图形叫做轴对称图形,这条直线叫对称轴;判断一个图形是否是轴对称图形,关键是找它的对称轴,要想象沿着这条线翻折能不能重叠,据此解答。
【详解】在数字0、2、3、4、5、6、7、8、9中,轴对称图形有3个,分别是0、3、8。
【点睛】本题主要考查轴对称的辨识,关键是找到对称轴。
18. 中心 方向 角度
【分析】在平面内,将一个图形绕一点按某个方向转动一个角度,这样的运动叫作图形的旋转,图形旋转有三个要素:中心点,方向,度数据此作答。
【详解】图形旋转有三个要素:中心点,方向,度数。
【点睛】考查了对图形旋转三个关键要素的理解和掌握情况。需要注意的是,因为三个要素共同决定了图形的旋转,所以允许答案有先后顺序的改变。
19.√
【分析】画出直角三角形,绕顶点旋转,(想象也可以),研究它的形状进行判断。
【详解】直角三角形绕某一点旋转90度,得到的图形仍然是直角三角形,所以判断正确。
【点睛】当图形经旋转变换时,大小和形状不会改变,这是解题的关键。
20.×
【分析】根据平移和旋转的定义,直接判断即可。平移是指图形的平行移动,平移时图形中所有点移动的方向一致,并且移动的距离相等;把一个图形绕着某一点转动一定角度的图形变换叫做旋转。
【详解】钟表上分针的运动属于旋转,题干说法错误。
故答案为:×
【点睛】本题是考查图形的旋转、平移的意义。旋转与平移的相同点:位置发生变化,大小不变,形状不变,都在一个平面内;不同点:平移时运动方向不变,旋转是围绕一个点或轴做圆周运动。
21.√
【分析】旋转是把图形绕着一点旋转一定的角度;平移是把一个图形整体沿某一直线方向移动;不论平移还是旋转,图形的形状、大小都不发生改变,只是位置变化了,据此判断即可。
【详解】由分析可得,一个图形平移或者旋转后只是位置变化了,而图形的形状不改变。题干说法正确。
故答案为:√
【点睛】此题主要考查了平移、旋转的性质。
22.√
【分析】如果一个图形沿一条直线折叠后,直线两旁的部分能够互相重合,那么这个图形叫做轴对称图形,这条直线叫做它的对称轴,由此可知,等腰三角形是轴对称图形。
【详解】根据轴对称的定义,等腰三角形是轴对称图形
故答案为:√
【点睛】正确理解轴对称图形的概念是解答此题的关键。
23.√
【分析】根据轴对称图形的意义分析解答即可,如果一个图形沿一条直线对折,直线两旁的部分能够互相重合,这个图形叫做轴对称图形。
【详解】五角星共有5条对称轴,过每个角的顶点都有1条对称轴,所以判断正确。
【点睛】本题主要考查轴对称图形的意义,明确轴对称图形的意义是解题关键。
24.√
【分析】根据旋转的特征,一个图形绕某一点按顺时针或逆时针旋转180°,某点的位置不动,其余各部分均绕此点按相同方向旋转相同的度数,旋转得到的图形互相重合,即得到图形的方向位置相同。
【详解】根据旋转的特征,一个图形绕同一点顺时针旋转180°和逆时针旋转180°后,得到图形的方向位置相同。
故答案为:√
【点睛】此题主要是考查旋转的意义及特征,一个图形绕某点顺时针或逆时针旋转180°,两图互相重合。
25.×
【分析】根据轴对称图形的意义:如果一个图形沿着一条直线对折后两部分完全重合,这样的图形叫做轴对称图形,这条直线叫做对称轴;据此判断。
【详解】等腰三角形、正方形、圆形都是轴对称图形,平行四边形不是轴对称图形;
故答案为:×
【点睛】判断是不是轴对称图形的关键是找出对称轴,图形两部分沿对称轴折叠后能完全重合。
26.(1)右;6
(2)见详解
【分析】(1)以一个点为基准,通过数格看这一点从左向右平移了几格,图形就平移了几格;
(2)过三角形的斜边画对称轴,然后以对称轴为中线,对称画出另一半;
(3)将梯形的四个顶点全部向上平移5个格,然后连线即可。
【详解】(1)通过看图可知,图形从左向右平移了6格。
(2)和(3)如下图;
【点睛】此题主要考查学生对图形平移、对称的理解与应用。
27.
【详解】先找出平行四边形的另外三个顶点绕点O顺时针旋转90°后的对应点的位置,然后顺次连接即可得出第一次旋转后的图形1,同样的方法,画出图形1顺时针旋转90度后的图形2,再画出图形2顺时针旋转90度后的图形3;据此即可解答.
28.(1)6;5;南;东45°;3;(2)(3)见详解。
【分析】(1)根据数对表示位置的方法:第一个数字表示所在列,第二个数字表示所在行;
(2)找到旗子主要的四个点平移后的位置,再连接各点即可得到图形①;
(3)小旗子绕点O按顺时针方向旋转90°后得到新的点,顺次连接可得图形②。
【详解】(1)B点的位置是(6,5),在A点的南偏东40°方向约3cm处;
(2)(3)如图:
【点睛】本题综合考查了数对表示位置、方向和位置、作平移后的图形,作旋转一定角度后的图形。
29.
【分析】仔细观察,可发现,第二个图形是第一个图形逆时针旋转一格得来,第三个图形是根据第二个图形逆时针旋转一格得来,据此解答。
【详解】根据观察分析,只需将第三个图形做逆时针旋转即可,如图:
【点睛】本题主要考查通过观察、猜测、推理等找出图形的排列规律和图形的旋转。
30.(1)答:能得到一棵完整的松树的是第二个。
(2)答:要想得到六边形,第二种剪法是正确的。
31.(1)图案(2)可以由基本图形顺时针90°旋转三次形成。
(2)图案(3),(7)可以经过平移得到;图形(1),(2),(4),(6),(8)可以经过旋转得到;图形(4),(5),(7),(8)可以经过轴对称得到。
【分析】当物体水平方向或竖直方向运动,并且物体的方向不发生改变,这种运动是平移。
在平面内,一个图形绕着一个定点旋转一定的角度得到另一个图形的变化就是旋转。
轴对称图形:平面内,一个图形沿一条直线折叠,直线两旁的部分能够完全重合的图形。
【详解】根据平移、旋轴、轴对称的定义分析可知:
(1)图案(2)可以由基本图形顺时针90°旋转三次形成。
(2)图案(3),(7)可以经过平移得到;图形(1),(2),(4),(6),(8)可以经过旋转得到;图形(4),(5),(7),(8)可以经过轴对称得到。
【点睛】理解平移、旋轴、轴对称的定义是解答此题的关键。
32.(1)下;6;
(2)见详解
【分析】(1)根据图示可知,②在①的下面,所以是向下平移;根据平移的特征,找到图形①各点与图形②的对应点,数出平移的格数即可。
(2)根据旋转的特征,三角形绕点O逆时针旋转90°,点O的位置不动,这个图形的各部分均绕此点按相同方向旋转相同的度数即可画出旋转后的图形。
【详解】(1)帆船①向下移6格得到帆船②;
(2)三角形绕点O逆时针旋转90 后的图形如下图红色所示。
【点睛】本题考查了图形的平移、旋转变化,学生主要看清是顺时针还是逆时针旋转,旋转多少度,难度不大,但易错。
33.15-6=9(cm)
学校:___________姓名:___________班级:___________考号:__________
一、选择题
1.下面的图形中,( )是旋转而成的;( )是轴对称图形。
① ② ③
A.③① B.①② C.②③
2.有4条对称轴的图形是( ).
A.三角形 B.圆 C.正方形
3.下列字母中,是轴对称图形的是( )
A.Q B.W C.R
4.从镜子中看到的左边图形的样子是( )
A. B. C.
5.如下图阴影部分,可以看作是一个菱形通过( )得到的图形.
A.平移 B.旋转 C.对称
6.汽车在公路上运动时,轮子的运动是( ).
A.平移 B.旋转 C.既平移又旋转
7.图形“”围绕“·”顺时针旋转90°后的图形是( )。
A.
B.
C.
8.如图中大正方形的边长是20厘米,阴影部分的面积是( )平方厘米。
A.50 B.100 C.150
9.下面第( )幅图是的水中倒影。
A. B. C.
二、填空题
10.从下午3时到下午7时,钟面上的时针旋转了( )度。
11.
(1)图形B可以看作图形A绕点( )顺时针方向旋转90°得到的。
(2)图形C可以看作图形B绕点O顺时针方向旋转( )得到的。
(3)图形B绕点O顺时针旋转180°到图形( )所在位置。
(4)图形D可以看作图形C绕点O顺时针方向旋转( )得到的。
12.过一点可以画( )条直线。 一个圆有( )条对称轴。
13.下面的英文字母可以看做是轴对称图形的有:________.
14.钟面上,时针从数字“2”顺时针旋转到数字“5”旋转了( )度;时针从数字“4”顺时针旋转60°到数字( )。
15.平移和旋转不改变图形的( )和( ),只改变图形的位置和方向。
16.填空题
(1)升国旗时国旗的运动属于_____运动;
(2)钟摆的运动属于_____运动;
(3)在算盘上的拨珠的运动属于_____运动;
(4)电梯的运动属于_____运动;
(5)风扇叶片的运动属于_____运动;
(6)运动的火车的运动属于_____运动;
(7)光盘在电脑里的运动属于_____运动。
17.在数字0、2、3、5、8、9中,( )是轴对称的数字。
18.图形的旋转有三个要素,一是旋转的( ),二是旋转的( ),三是旋转的( )。
三、判断题
19.直角三角形绕某一点旋转后得到的图形仍然是直角三角形。( )
20.钟表上分针的运动属于平移。( )
21.一个图形平移或者旋转后只是位置变化了,而图形的形状不改变。( )
22.等腰三角形是轴对称图形。( )
23.五角星有5条对称轴。( )
24.一个长方形绕某点顺时针旋转180°和逆时针旋转180°得到图形位置完全一样。( )
25.等腰三角形、正方形、平行四边形、圆形都是轴对称图形。( )
四、解答题
26.
(1)向( )平移了( )格。
(2)画出的另一半,使它成为轴对称图形,并画出它的一条对称轴。
(3)画出向上平移5个方格后的图形。
27.将下面的平行四边形绕顶点O顺时针旋转,每次旋转90°,旋转3次.
28.在下面图中完成如下操作,并回答问题:
(1)B点的位置是(________,________),在A点的________偏________方向约________cm处。
(2)小旗子向右平移9格后的图形。
(3)小旗子绕O点顺时针方向旋转90°的图形。
29.这里的规律你知道吗?接下来该怎么排?
30.想一想,圈一圈。
(1)如图,把一张正方形纸对折,沿虚线剪,能得到一棵完整的松树的是哪一个?
(2)要想得到六边形,下列哪种剪法是正确的?
31.在现实生活中,我们经常见到一些美丽的图案。
(1)请你分析图案(2)的形成过程?
(2)哪几个图案可以经过平移得到?哪几个图案可以经过旋转得到?哪几个图案可以经过轴对称得到?
32.
(1)帆船①向( )平移( )格得到帆船②。
(2)画出三角形绕点O逆时针旋转90 后的图形。
33.将三角形ABC沿边AB向右平移6 cm,得到三角形DEF。已知AB=15 cm,求BD的长。
参考答案:
1.A
【分析】如果一个图形沿着一条直线对折后两部分完全重合,这样的图形叫做轴对称图形,这条直线叫做对称轴;如果一个图形绕某一点旋转一定的角度后能够与自身重合,那么这个图形就叫做旋转对称图形,这个点叫做旋转中心;据此对各图形分析后即可得解。
【详解】①是轴对称图形;
②不是旋转而成的图形,也不是轴对称图形;
③是旋转而成的图形;
故答案为:A。
【点睛】此题主要考查了旋转和轴对称在实际当中的运用。
2.C
3.B
4.C
【详解】根据镜面对称的特征,镜中的景物与实际景物上下前后方向一致,左右方向相反,大小不变,且关于镜面对称.镜面对称的特点是:上下前后方向一致,左右方向相反,镜中与实际景物大小不变.
从镜子中看到的左边图形的样子是 ;
故选C.
5.B
【详解】看图可知,菱形ABCD以A为中心,逆时针旋转得到菱形AEFG;据此选择即可.
6.B
7.A
8.B
【分析】如下图,把四个阴影部分的三角形平移后拼在一起,可以形成一个边长为20÷2=10厘米的小正方形,求出小正方形的面积即可解答。
【详解】20÷2=10(厘米),10×10=100(平方厘米)。
故答案为:B。
【点睛】本题主要考查学生的观察和分析能力。
9.C
【分析】要求房子的水中倒影,其实就是求房子关于水面的轴对称图形,将房子的各点相对于水面进行对称标点,然后再连接即可解答。
【详解】通过观察房子的轴对称图形可知,通过比对烟筒、窗户、门的位置即可判断出C图正确。
故答案为:C
【点睛】此题主要考查学生对轴对称图形的理解与认识,需要理解对称的定义和观察方法,需要认真仔细。
10.120
【分析】因为时钟的的圆周为360°,可以分为四份,每份90°(每90°包含了三个30°)。从下午3时走到6时,正好是90°,走到7时,也就是多了30°,90°加30°,正好是120°。
【详解】从下午3时到下午7时,用算式表达:360°÷4+30°=120°。
所以钟面上的时针旋转了120度。
【点睛】本题主要考查旋转的应用,角度的度量和钟表辨识,解答此题的关键是弄清从下午3时到晚上7时时针在钟面上运动的轨迹。
11. O 90° D 90°
【分析】决定旋转后图形的位置的要素:一是旋转中心或轴,二是旋转方向(顺时针或逆时针),三是旋转角度。
【详解】(1)图形B可以看作图形A绕点O顺时针方向旋转90°得到的;
(2)图形C可以看作图形B绕点O顺时针方向旋转90°得到的;
(3)图形B绕点O顺时针旋转180°到图形D所在位置;
(4)图形D可以看作图形C绕点O顺时针方向旋转90°得到的。
【点睛】本题考查了旋转与旋转现象,物体或图形旋转后,它们的形状、大小都不改变,只是位置发生了变化。
12. 无数 无数
13.①②③④⑦
【详解】轴对称图形是说如果一个图形沿着一条直线对折后两部分完全重合.由此可以断定以上字母可以看做轴对称图形的有①、②、③、④、⑦.
14. 90 6
【分析】钟面上,相邻两个数字间的角度是30°。先利用减法求出从“2”到“5”,时针旋转了几个数字,再乘30°,即可求出时针从数字“2”顺时针旋转到数字“5”旋转了多少度;
用60°除以30°,求出时针旋转了几个数字,再利用加法求出时针从数字“4”顺时针旋转60°到了数字几。
【详解】(5-2)×30°
=3×30°
=90°
60°÷30°+4
=2+4
=6
所以,钟面上,时针从数字“2”顺时针旋转到数字“5”旋转了90度;时针从数字“4”顺时针旋转60°到数字6。
【点睛】本题考查了旋转现象以及钟面的认识,明确钟面上相邻两个数字间的度数是解题的关键。
15. 大小 形状
【详解】平移是指在平面内,将一个图形上的所有点都按照某个方向作相同距离的移动。平移不改变图形的形状和大小,只是改变位置。把一个图形绕着某一点转动一个角度的图形变换叫做旋转,旋转时图形位置发生变化,大小不变,形状不变。所以平移和旋转不改变图形的大小和形状,只改变图形的位置和方向。
16. 平移 旋转 平移 平移 旋转 平移 旋转
【分析】根据旋转的含义,物体绕着某一点或轴运动,这种运动现象称为旋转;平移是指在平面内,将一个图形上的所有点都按照某个方向作相同距离的移动,这样的图形运动叫作图形的平移运动,据此解答。
【详解】(1)升国旗时国旗的运动属于平移运动;
(2)钟摆的运动属于旋转运动;
(3)在算盘上的拨珠的运动属于平移运动;
(4)电梯的运动属于平移运动;
(5)风扇叶片的运动属于旋转运动;
(6)运动的火车的运动属于平移运动;
(7)光盘在电脑里的运动属于旋转运动。
故答案为:(1)平移 (2)旋转 (3)平移 (4)平移 (5)旋转 (6)平移 (7)旋转
【点睛】本题考查了如何判定生活中的旋转现象和平移现象,牢记要点,旋转是绕着某个固定点旋转一定的角度,一般情况下方向会发生改变。平移是沿某一方向移动一定的距离。
17.0、3、8
【分析】如果一个平面图形沿着一条直线折叠后,直线两旁的部分能够互相重合,那么这个图形叫做轴对称图形,这条直线叫对称轴;判断一个图形是否是轴对称图形,关键是找它的对称轴,要想象沿着这条线翻折能不能重叠,据此解答。
【详解】在数字0、2、3、4、5、6、7、8、9中,轴对称图形有3个,分别是0、3、8。
【点睛】本题主要考查轴对称的辨识,关键是找到对称轴。
18. 中心 方向 角度
【分析】在平面内,将一个图形绕一点按某个方向转动一个角度,这样的运动叫作图形的旋转,图形旋转有三个要素:中心点,方向,度数据此作答。
【详解】图形旋转有三个要素:中心点,方向,度数。
【点睛】考查了对图形旋转三个关键要素的理解和掌握情况。需要注意的是,因为三个要素共同决定了图形的旋转,所以允许答案有先后顺序的改变。
19.√
【分析】画出直角三角形,绕顶点旋转,(想象也可以),研究它的形状进行判断。
【详解】直角三角形绕某一点旋转90度,得到的图形仍然是直角三角形,所以判断正确。
【点睛】当图形经旋转变换时,大小和形状不会改变,这是解题的关键。
20.×
【分析】根据平移和旋转的定义,直接判断即可。平移是指图形的平行移动,平移时图形中所有点移动的方向一致,并且移动的距离相等;把一个图形绕着某一点转动一定角度的图形变换叫做旋转。
【详解】钟表上分针的运动属于旋转,题干说法错误。
故答案为:×
【点睛】本题是考查图形的旋转、平移的意义。旋转与平移的相同点:位置发生变化,大小不变,形状不变,都在一个平面内;不同点:平移时运动方向不变,旋转是围绕一个点或轴做圆周运动。
21.√
【分析】旋转是把图形绕着一点旋转一定的角度;平移是把一个图形整体沿某一直线方向移动;不论平移还是旋转,图形的形状、大小都不发生改变,只是位置变化了,据此判断即可。
【详解】由分析可得,一个图形平移或者旋转后只是位置变化了,而图形的形状不改变。题干说法正确。
故答案为:√
【点睛】此题主要考查了平移、旋转的性质。
22.√
【分析】如果一个图形沿一条直线折叠后,直线两旁的部分能够互相重合,那么这个图形叫做轴对称图形,这条直线叫做它的对称轴,由此可知,等腰三角形是轴对称图形。
【详解】根据轴对称的定义,等腰三角形是轴对称图形
故答案为:√
【点睛】正确理解轴对称图形的概念是解答此题的关键。
23.√
【分析】根据轴对称图形的意义分析解答即可,如果一个图形沿一条直线对折,直线两旁的部分能够互相重合,这个图形叫做轴对称图形。
【详解】五角星共有5条对称轴,过每个角的顶点都有1条对称轴,所以判断正确。
【点睛】本题主要考查轴对称图形的意义,明确轴对称图形的意义是解题关键。
24.√
【分析】根据旋转的特征,一个图形绕某一点按顺时针或逆时针旋转180°,某点的位置不动,其余各部分均绕此点按相同方向旋转相同的度数,旋转得到的图形互相重合,即得到图形的方向位置相同。
【详解】根据旋转的特征,一个图形绕同一点顺时针旋转180°和逆时针旋转180°后,得到图形的方向位置相同。
故答案为:√
【点睛】此题主要是考查旋转的意义及特征,一个图形绕某点顺时针或逆时针旋转180°,两图互相重合。
25.×
【分析】根据轴对称图形的意义:如果一个图形沿着一条直线对折后两部分完全重合,这样的图形叫做轴对称图形,这条直线叫做对称轴;据此判断。
【详解】等腰三角形、正方形、圆形都是轴对称图形,平行四边形不是轴对称图形;
故答案为:×
【点睛】判断是不是轴对称图形的关键是找出对称轴,图形两部分沿对称轴折叠后能完全重合。
26.(1)右;6
(2)见详解
【分析】(1)以一个点为基准,通过数格看这一点从左向右平移了几格,图形就平移了几格;
(2)过三角形的斜边画对称轴,然后以对称轴为中线,对称画出另一半;
(3)将梯形的四个顶点全部向上平移5个格,然后连线即可。
【详解】(1)通过看图可知,图形从左向右平移了6格。
(2)和(3)如下图;
【点睛】此题主要考查学生对图形平移、对称的理解与应用。
27.
【详解】先找出平行四边形的另外三个顶点绕点O顺时针旋转90°后的对应点的位置,然后顺次连接即可得出第一次旋转后的图形1,同样的方法,画出图形1顺时针旋转90度后的图形2,再画出图形2顺时针旋转90度后的图形3;据此即可解答.
28.(1)6;5;南;东45°;3;(2)(3)见详解。
【分析】(1)根据数对表示位置的方法:第一个数字表示所在列,第二个数字表示所在行;
(2)找到旗子主要的四个点平移后的位置,再连接各点即可得到图形①;
(3)小旗子绕点O按顺时针方向旋转90°后得到新的点,顺次连接可得图形②。
【详解】(1)B点的位置是(6,5),在A点的南偏东40°方向约3cm处;
(2)(3)如图:
【点睛】本题综合考查了数对表示位置、方向和位置、作平移后的图形,作旋转一定角度后的图形。
29.
【分析】仔细观察,可发现,第二个图形是第一个图形逆时针旋转一格得来,第三个图形是根据第二个图形逆时针旋转一格得来,据此解答。
【详解】根据观察分析,只需将第三个图形做逆时针旋转即可,如图:
【点睛】本题主要考查通过观察、猜测、推理等找出图形的排列规律和图形的旋转。
30.(1)答:能得到一棵完整的松树的是第二个。
(2)答:要想得到六边形,第二种剪法是正确的。
31.(1)图案(2)可以由基本图形顺时针90°旋转三次形成。
(2)图案(3),(7)可以经过平移得到;图形(1),(2),(4),(6),(8)可以经过旋转得到;图形(4),(5),(7),(8)可以经过轴对称得到。
【分析】当物体水平方向或竖直方向运动,并且物体的方向不发生改变,这种运动是平移。
在平面内,一个图形绕着一个定点旋转一定的角度得到另一个图形的变化就是旋转。
轴对称图形:平面内,一个图形沿一条直线折叠,直线两旁的部分能够完全重合的图形。
【详解】根据平移、旋轴、轴对称的定义分析可知:
(1)图案(2)可以由基本图形顺时针90°旋转三次形成。
(2)图案(3),(7)可以经过平移得到;图形(1),(2),(4),(6),(8)可以经过旋转得到;图形(4),(5),(7),(8)可以经过轴对称得到。
【点睛】理解平移、旋轴、轴对称的定义是解答此题的关键。
32.(1)下;6;
(2)见详解
【分析】(1)根据图示可知,②在①的下面,所以是向下平移;根据平移的特征,找到图形①各点与图形②的对应点,数出平移的格数即可。
(2)根据旋转的特征,三角形绕点O逆时针旋转90°,点O的位置不动,这个图形的各部分均绕此点按相同方向旋转相同的度数即可画出旋转后的图形。
【详解】(1)帆船①向下移6格得到帆船②;
(2)三角形绕点O逆时针旋转90 后的图形如下图红色所示。
【点睛】本题考查了图形的平移、旋转变化,学生主要看清是顺时针还是逆时针旋转,旋转多少度,难度不大,但易错。
33.15-6=9(cm)
