2022-2023学年人教版七年级数学下册9.2.1 一元一次不等式的解法 课件 (共22张PPT)
文档属性
| 名称 | 2022-2023学年人教版七年级数学下册9.2.1 一元一次不等式的解法 课件 (共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-15 00:00:00 | ||
图片预览








文档简介
(共22张PPT)
一元一次不等式的解法
1. 理解和掌握一元一次不等式的概念;
2. 会用不等式的性质熟练地解一元一次不等式. (重点、难点)
不等式的性质1:
不等式的性质2:
不等式的性质3:
不等式两边加(或减)同一个数(或式子),不等号的方向不变.
如果 a>b,那么 a±c>b±c.
不等式两边乘(或除以)同一个负数,不等号的方向改变.
如果 a>b,c<0,那么 ac<bc (或< ).
不等式两边乘(或除以)同一个正数,不等号的方向不变.
如果 a>b,c>0,那么 ac>bc (或> ).
观察下面的不等式:x-7>26,3x<2x+1,x>50,-4x>3.它们有哪些共同特征?
上述每个不等式都只含有一个未知数,并且未知数的次数是1.
类似于一元一次方程,含有一个未知数,未知数的次数是1的不等式,叫做一元一次不等式.
例1.下列式子中,是一元一次不等式的有哪些?
(1)3x+5=0;(2)2x+3>5;(3);(4)≥2;(5)2x+y≤8.
解:(1)是等式;(4)不等式的左边不是整式;(5)含有两个未知数,所以不是一元一次不等式,
所以一元一次不等式有:(2)(3)
利用不等式的性质将下列不等式进行变形:
(1)在不等式x-7>26的两边同时加7得______;
(2)在不等式3x<2x+1的两边同时减去2x得______;
x>33
x<1
归纳:不等式两边同时加减一个数或式子,相当于将其改变符号后移到另一边.
x>26+7,3x-2x<1
利用不等式的性质将下列不等式进行变形:
(3)在不等式x>50的两边同时乘得______;
(4)在不等式-4x>3的两边同时除以-4得_______.
归纳:不等式两边同时除以未知数的系数(或乘未知数系数的倒数),相当于系数化为1.
x>50×
注意:当这个系数为负数时,不等号的方向要改变.
x>75
x<-
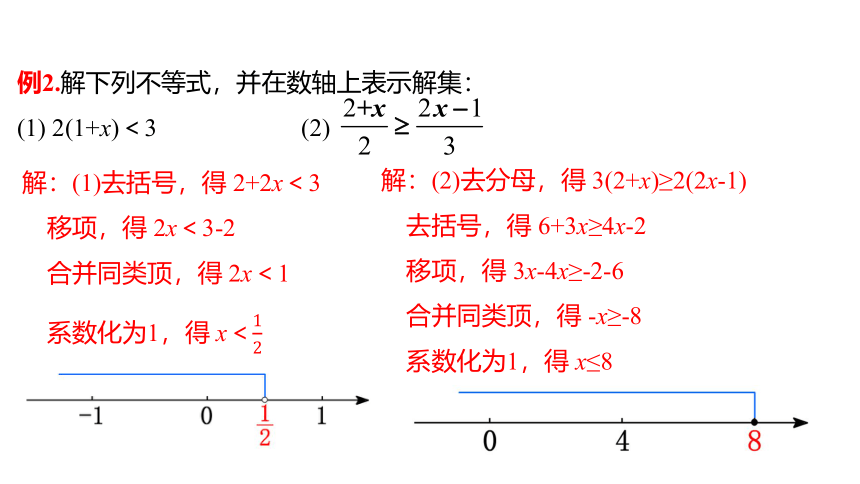
例2.解下列不等式,并在数轴上表示解集:
(1) 2(1+x)<3 (2)
解:(1)去括号,得 2+2x<3
移项,得 2x<3-2
合并同类顶,得 2x<1
系数化为1,得 x<
解:(2)去分母,得 3(2+x)≥2(2x-1)
去括号,得 6+3x≥4x-2
移项,得 3x-4x≥-2-6
合并同类顶,得 -x≥-8
系数化为1,得 x≤8
1.解一元一次方程,要根据等式的性质,将方程逐步化为x=a的形式;而解一元一次不等式,则要根据不等式的性质,将不等式逐步化为x<a或x>a的形式.
2.解一元一次不等式与解一元一次方程一样,都是通过“去分母、去括号、移项、合并同类项、系数化为1”几个步骤确定答案.
3.如果未知数的系数为负数,那么在系数化为1时,要改变不等号的方向.
4.在数轴上表示不等式的解集,大于向右画线,小于向左画线,界点有等号画实心圆点,无等号画空心圆圈.
解下列不等式,并在数轴上表示解集:
(1) 5x+15>4x-1 (2) 2(x+5)≤3(x-5) (3) (4)
解:(1)移项,得 5x-4x>-1-15
合并同类项,得 x>-16
解:(2)去括号,得 2x+10≤3x-15
移项,得 2x-3x≤-15-10
合并同类项,得 -x≤-25
系数化为1,得 x≥25
解下列不等式,并在数轴上表示解集:
(1) 5x+15>4x-1 (2) 2(x+5)≤3(x-5) (3) (4)
解:(3)去分母,得 3(x-1)<7(2x+5)
去括号,得 3x-3<14x+35
移项,得 3x-14x<35+3
合并同类项,得 -11x<38
系数化为1,得 x>-
解:(4)去分母,得 2(x+1)≥3(2x-5)+12
去括号,得 2x+2≥6x-15+12
移项,得 2x-6x≥-15+12-2
合并同类项,得 -4x≥-5
系数化为1,得 x≤
例3.已知关于的方程的解为负数,求的取值范围.
解:
去分母得,
去括号得,,
移项合并得,,
系数化为1得:,
∵,
解得,
∴的取值范围为.
取何值时,关于的方程的解大于.
解:解方程得,
由题意知,
解得:.
例4.若关于x,y的二元一次方程组的解满足,求m的取值范围.
解:,
由得:,
由得:,
,
,
解得.
已知关于x,y的二元一次方程组的解满足,求a的负整数值.
解:,
,得:,
∴,
∵,
∴,
∴,
∴a的负整数值为:.
1.下列不等式中,是一元一次不等式的是( )
A.3x- 2y<-1 B.-1< 2 C.2x-1>0 D. y2+3> 5x-1
2.在解不等式当 - ≤1时,去分母正确的是( )
A. 2x-3x-3≤6 B.2x-3(x-1)≤6 C.2x-3x-3≤1 D.2x-3(x-1)≤1
3.关于x的不等式-2x+a≥2的解集在数轴上如图所示,则a的值是( )
A.0 B.2 C.-2 D. -4
C
B
A
4.不等式3x-1>5的解集是________.
5.代数式-1值为正数,m的范围是________.
6.若x是非负数,则-1≤的解集是____________.
7.三个连续整数的和小于10,且最小的整数大于1,则这三个连续整数中,最大的整数为______.
8.关于x的不等式3x-a≤0, 只有两个正整数解,则a的取值范围是___________.
x>2
m>4
0≤m≤4
4
6≤m<9
9.解不等式,并把它的解集在数轴上表示出来.
(1); (2);
(1)解:去括号得:,
移项得:,
合并同类项得:,
化系数为1得:;
(2)解:去分母得:,
去括号得:,
移项得:,
合并同类项得:,
化系数为1得:;
9.解不等式,并把它的解集在数轴上表示出来.
(3)(4)
(3)解:移项得:,
合并同类项得:,
化系数为1得:;
(4)解:去括号得:,
移项得:,
合并同类项得:,
化系数为1得:.
10.解不等式,并写出它的所有正整数解.
解:去分母,得,
去括号,得,
移项,得,
合并同类项,得,
系数化为1,得,
则不等式的正整数解为:1,2,3,4,5.
11.已知关于x的不等式(2a-b)x+a-5b>0的解集是x<求关于x的不等式ax>b的解集.
解:由(2a-b)x+a-5b>0, 得(2a-b)x> -a+5b
∵x<,∴2a-b<0,∴x<
也就是说
整理得35b-7a=20a-10b,27a=45b,=,b=a,
∵2a-b<0,∴2a-a<0,a<0,∴a<0
∴ax>b的解集是x<,即x<
类似于一元一次方程,含有一个未知数,未知数的次数是1的不等式,叫做一元一次不等式.
1.解一元一次方程,要根据等式的性质,将方程逐步化为x=a的形式;而解一元一次不等式,则要根据不等式的性质,将不等式逐步化为x<a或x>a的形式.
2.解一元一次不等式与解一元一次方程一样,都是通过“去分母、去括号、移项、合并同类项、系数化为1”几个步骤确定答案.
3.如果未知数的系数为负数,那么在系数化为1时,要改变不等号的方向.
4.在数轴上表示不等式的解集,大于向右画线,小于向左画线,界点有等号画实心圆点,无等号画空心圆圈.
★解一元一次不等式的基本要求:
一元一次不等式的解法
1. 理解和掌握一元一次不等式的概念;
2. 会用不等式的性质熟练地解一元一次不等式. (重点、难点)
不等式的性质1:
不等式的性质2:
不等式的性质3:
不等式两边加(或减)同一个数(或式子),不等号的方向不变.
如果 a>b,那么 a±c>b±c.
不等式两边乘(或除以)同一个负数,不等号的方向改变.
如果 a>b,c<0,那么 ac<bc (或< ).
不等式两边乘(或除以)同一个正数,不等号的方向不变.
如果 a>b,c>0,那么 ac>bc (或> ).
观察下面的不等式:x-7>26,3x<2x+1,x>50,-4x>3.它们有哪些共同特征?
上述每个不等式都只含有一个未知数,并且未知数的次数是1.
类似于一元一次方程,含有一个未知数,未知数的次数是1的不等式,叫做一元一次不等式.
例1.下列式子中,是一元一次不等式的有哪些?
(1)3x+5=0;(2)2x+3>5;(3);(4)≥2;(5)2x+y≤8.
解:(1)是等式;(4)不等式的左边不是整式;(5)含有两个未知数,所以不是一元一次不等式,
所以一元一次不等式有:(2)(3)
利用不等式的性质将下列不等式进行变形:
(1)在不等式x-7>26的两边同时加7得______;
(2)在不等式3x<2x+1的两边同时减去2x得______;
x>33
x<1
归纳:不等式两边同时加减一个数或式子,相当于将其改变符号后移到另一边.
x>26+7,3x-2x<1
利用不等式的性质将下列不等式进行变形:
(3)在不等式x>50的两边同时乘得______;
(4)在不等式-4x>3的两边同时除以-4得_______.
归纳:不等式两边同时除以未知数的系数(或乘未知数系数的倒数),相当于系数化为1.
x>50×
注意:当这个系数为负数时,不等号的方向要改变.
x>75
x<-
例2.解下列不等式,并在数轴上表示解集:
(1) 2(1+x)<3 (2)
解:(1)去括号,得 2+2x<3
移项,得 2x<3-2
合并同类顶,得 2x<1
系数化为1,得 x<
解:(2)去分母,得 3(2+x)≥2(2x-1)
去括号,得 6+3x≥4x-2
移项,得 3x-4x≥-2-6
合并同类顶,得 -x≥-8
系数化为1,得 x≤8
1.解一元一次方程,要根据等式的性质,将方程逐步化为x=a的形式;而解一元一次不等式,则要根据不等式的性质,将不等式逐步化为x<a或x>a的形式.
2.解一元一次不等式与解一元一次方程一样,都是通过“去分母、去括号、移项、合并同类项、系数化为1”几个步骤确定答案.
3.如果未知数的系数为负数,那么在系数化为1时,要改变不等号的方向.
4.在数轴上表示不等式的解集,大于向右画线,小于向左画线,界点有等号画实心圆点,无等号画空心圆圈.
解下列不等式,并在数轴上表示解集:
(1) 5x+15>4x-1 (2) 2(x+5)≤3(x-5) (3) (4)
解:(1)移项,得 5x-4x>-1-15
合并同类项,得 x>-16
解:(2)去括号,得 2x+10≤3x-15
移项,得 2x-3x≤-15-10
合并同类项,得 -x≤-25
系数化为1,得 x≥25
解下列不等式,并在数轴上表示解集:
(1) 5x+15>4x-1 (2) 2(x+5)≤3(x-5) (3) (4)
解:(3)去分母,得 3(x-1)<7(2x+5)
去括号,得 3x-3<14x+35
移项,得 3x-14x<35+3
合并同类项,得 -11x<38
系数化为1,得 x>-
解:(4)去分母,得 2(x+1)≥3(2x-5)+12
去括号,得 2x+2≥6x-15+12
移项,得 2x-6x≥-15+12-2
合并同类项,得 -4x≥-5
系数化为1,得 x≤
例3.已知关于的方程的解为负数,求的取值范围.
解:
去分母得,
去括号得,,
移项合并得,,
系数化为1得:,
∵,
解得,
∴的取值范围为.
取何值时,关于的方程的解大于.
解:解方程得,
由题意知,
解得:.
例4.若关于x,y的二元一次方程组的解满足,求m的取值范围.
解:,
由得:,
由得:,
,
,
解得.
已知关于x,y的二元一次方程组的解满足,求a的负整数值.
解:,
,得:,
∴,
∵,
∴,
∴,
∴a的负整数值为:.
1.下列不等式中,是一元一次不等式的是( )
A.3x- 2y<-1 B.-1< 2 C.2x-1>0 D. y2+3> 5x-1
2.在解不等式当 - ≤1时,去分母正确的是( )
A. 2x-3x-3≤6 B.2x-3(x-1)≤6 C.2x-3x-3≤1 D.2x-3(x-1)≤1
3.关于x的不等式-2x+a≥2的解集在数轴上如图所示,则a的值是( )
A.0 B.2 C.-2 D. -4
C
B
A
4.不等式3x-1>5的解集是________.
5.代数式-1值为正数,m的范围是________.
6.若x是非负数,则-1≤的解集是____________.
7.三个连续整数的和小于10,且最小的整数大于1,则这三个连续整数中,最大的整数为______.
8.关于x的不等式3x-a≤0, 只有两个正整数解,则a的取值范围是___________.
x>2
m>4
0≤m≤4
4
6≤m<9
9.解不等式,并把它的解集在数轴上表示出来.
(1); (2);
(1)解:去括号得:,
移项得:,
合并同类项得:,
化系数为1得:;
(2)解:去分母得:,
去括号得:,
移项得:,
合并同类项得:,
化系数为1得:;
9.解不等式,并把它的解集在数轴上表示出来.
(3)(4)
(3)解:移项得:,
合并同类项得:,
化系数为1得:;
(4)解:去括号得:,
移项得:,
合并同类项得:,
化系数为1得:.
10.解不等式,并写出它的所有正整数解.
解:去分母,得,
去括号,得,
移项,得,
合并同类项,得,
系数化为1,得,
则不等式的正整数解为:1,2,3,4,5.
11.已知关于x的不等式(2a-b)x+a-5b>0的解集是x<求关于x的不等式ax>b的解集.
解:由(2a-b)x+a-5b>0, 得(2a-b)x> -a+5b
∵x<,∴2a-b<0,∴x<
也就是说
整理得35b-7a=20a-10b,27a=45b,=,b=a,
∵2a-b<0,∴2a-a<0,a<0,∴a<0
∴ax>b的解集是x<,即x<
类似于一元一次方程,含有一个未知数,未知数的次数是1的不等式,叫做一元一次不等式.
1.解一元一次方程,要根据等式的性质,将方程逐步化为x=a的形式;而解一元一次不等式,则要根据不等式的性质,将不等式逐步化为x<a或x>a的形式.
2.解一元一次不等式与解一元一次方程一样,都是通过“去分母、去括号、移项、合并同类项、系数化为1”几个步骤确定答案.
3.如果未知数的系数为负数,那么在系数化为1时,要改变不等号的方向.
4.在数轴上表示不等式的解集,大于向右画线,小于向左画线,界点有等号画实心圆点,无等号画空心圆圈.
★解一元一次不等式的基本要求:
