17.1 勾股定理 同步训练必刷(无答案)2022-2023学年人教版数学八年级下册
文档属性
| 名称 | 17.1 勾股定理 同步训练必刷(无答案)2022-2023学年人教版数学八年级下册 |  | |
| 格式 | docx | ||
| 文件大小 | 360.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-15 16:28:22 | ||
图片预览

文档简介
17.1 勾股定理
一、单选题
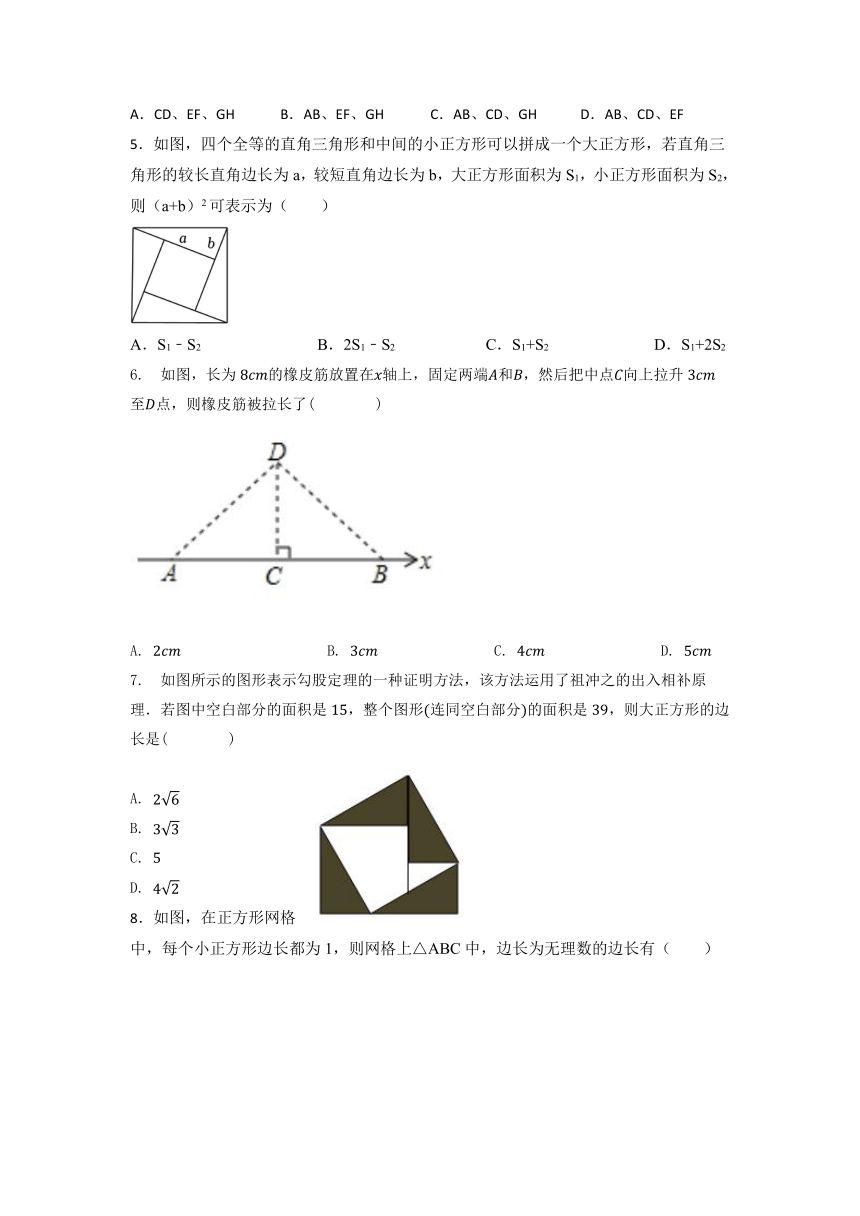
1.勾股定理是人类早期发现并证明的重要数学定理之一,是用代数思想解决几何问题的最重要的工具之一,也是数形结合的纽带之一.它不但因证明方法层出不穷吸引着人们,更因为应用广泛而使人入迷.如图,秋千静止时,踏板离地的垂直高度,将它往前推至处时(即水平距离),踏板离地的垂直高度,它的绳索始终拉直,则绳索的长是( )
A. B. C.6 D.
2.直角的斜边为5,一条直角边为4,则此三角形的面积是( )
A.10 B.20 C.12 D.6
3.如图,在四边形中,,,与关于直线轴对称,,,点与点对应,交于点,则线段的长为( )
A.5 B. C.4 D.
4.如图,在单位正方形组成的网格图中标有AB、CD、EF、GH四条线段,其中能构成一个直角三角形三边的线段是()
A.CD、EF、GH B.AB、EF、GH C.AB、CD、GH D.AB、CD、EF
5.如图,四个全等的直角三角形和中间的小正方形可以拼成一个大正方形,若直角三角形的较长直角边长为a,较短直角边长为b,大正方形面积为S1,小正方形面积为S2,则(a+b)2可表示为( )
A.S1﹣S2 B.2S1﹣S2 C.S1+S2 D.S1+2S2
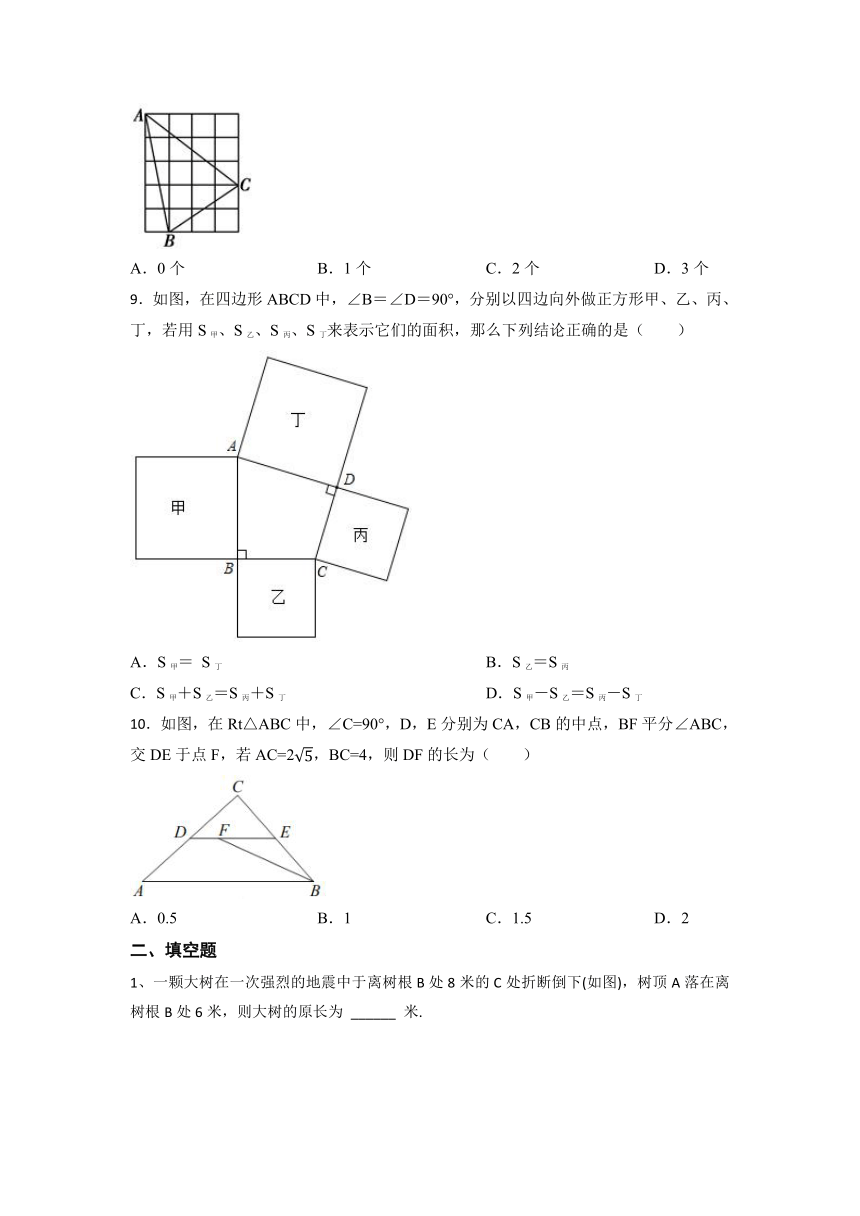
6. 如图,长为的橡皮筋放置在轴上,固定两端和,然后把中点向上拉升至点,则橡皮筋被拉长了( )
A. B. C. D.
7. 如图所示的图形表示勾股定理的一种证明方法,该方法运用了祖冲之的出入相补原理.若图中空白部分的面积是,整个图形连同空白部分的面积是,则大正方形的边长是( )
A.
B.
C.
D.
8.如图,在正方形网格中,每个小正方形边长都为1,则网格上△ABC中,边长为无理数的边长有( )
A.0个 B.1个 C.2个 D.3个
9.如图,在四边形ABCD中,∠B=∠D=90°,分别以四边向外做正方形甲、乙、丙、丁,若用S甲、S乙、S丙、S丁来表示它们的面积,那么下列结论正确的是( )
A.S甲= S丁 B.S乙=S丙
C.S甲+S乙=S丙+S丁 D.S甲-S乙=S丙-S丁
10.如图,在Rt△ABC中,∠C=90°,D,E分别为CA,CB的中点,BF平分∠ABC,交DE于点F,若AC=2,BC=4,则DF的长为( )
A.0.5 B.1 C.1.5 D.2
二、填空题
1、一颗大树在一次强烈的地震中于离树根B处8米的C处折断倒下(如图),树顶A落在离树根B处6米,则大树的原长为 ______ 米.
2、我国古代数学著作《九章算术》中有这样一个问题:“今有池方一丈,葭(jiā)生其中央,出水一尺,引葭赴岸,适与岸齐问水深几何?”(注:丈、尺是长度单位,1丈=10尺)这段话翻译成现代汉语,即为:如图,有一个水池,水面是一个边长为1丈的正方形,在水池正中央有一根芦苇,它高出水面1尺,如果把这根芦苇拉向水池一边的中点,它的顶端恰好到达池边的水面.则水池里水的深度是_______________尺.
3、如图,矩形ABCD中,,,E,F,Q分别是AD和BC、DC的中点,P是EF上的点,则的最小值为________.
4、如图,在中,,将线段绕点顺时针旋转至,过点作,垂足为,若,,则的长为__.
5、如图,AB⊥BC,CD⊥BC,垂足分别为B,C,P为线段BC上一点,连结PA,PD.已知AB=5,DC=4,BC=12,则AP+DP的最小值为_____.
6.一根直立于水中的芦节(BD)高出水面(AC)2米,一阵风吹来,芦苇的顶端D恰好到达水面的C处,且C到BD的距离AC=6米,水的深度(AB)为 米
三、解答题
1.如图,在和中,AB为斜边,AC=BD,BC、AD相交于点E
(1)请说明AE=BE的理由;
(2)若∠AEC=45°,AC=1,求CB的长.
2、如图和都是等腰直角三角形,,,顶点在的斜边上,求证:.
3、如图,在四边形ABCD中,∠B=∠D=90°,∠C=60°,AD=1,BC=2,求AB、CD的长.
4 勾股定理神秘而美妙,它的证法多样,其巧妙各有不同,当两个全等的直角三角形如图摆放时,也可以用面积法来证明勾股定理,请完成证明过程.
5 如图,将三角形纸片折叠,使点,都与点重合,折痕分别为,已知,,,求的长.
2.观察、思考与验证
(1)如图1是一个重要公式的几何解释,请你写出这个公式 .
(2)如图2所示,∠B=∠D=90°,且B,C,D在同一直线上.试说明:∠ACE=90°.
(3)伽菲尔德(1881年任美国第20届总统)利用(1)中的公式和图2证明了勾股定理(发表在1876年4月1日的<新英格兰教育日志》上),请你写出验证过程.
一、单选题
1.勾股定理是人类早期发现并证明的重要数学定理之一,是用代数思想解决几何问题的最重要的工具之一,也是数形结合的纽带之一.它不但因证明方法层出不穷吸引着人们,更因为应用广泛而使人入迷.如图,秋千静止时,踏板离地的垂直高度,将它往前推至处时(即水平距离),踏板离地的垂直高度,它的绳索始终拉直,则绳索的长是( )
A. B. C.6 D.
2.直角的斜边为5,一条直角边为4,则此三角形的面积是( )
A.10 B.20 C.12 D.6
3.如图,在四边形中,,,与关于直线轴对称,,,点与点对应,交于点,则线段的长为( )
A.5 B. C.4 D.
4.如图,在单位正方形组成的网格图中标有AB、CD、EF、GH四条线段,其中能构成一个直角三角形三边的线段是()
A.CD、EF、GH B.AB、EF、GH C.AB、CD、GH D.AB、CD、EF
5.如图,四个全等的直角三角形和中间的小正方形可以拼成一个大正方形,若直角三角形的较长直角边长为a,较短直角边长为b,大正方形面积为S1,小正方形面积为S2,则(a+b)2可表示为( )
A.S1﹣S2 B.2S1﹣S2 C.S1+S2 D.S1+2S2
6. 如图,长为的橡皮筋放置在轴上,固定两端和,然后把中点向上拉升至点,则橡皮筋被拉长了( )
A. B. C. D.
7. 如图所示的图形表示勾股定理的一种证明方法,该方法运用了祖冲之的出入相补原理.若图中空白部分的面积是,整个图形连同空白部分的面积是,则大正方形的边长是( )
A.
B.
C.
D.
8.如图,在正方形网格中,每个小正方形边长都为1,则网格上△ABC中,边长为无理数的边长有( )
A.0个 B.1个 C.2个 D.3个
9.如图,在四边形ABCD中,∠B=∠D=90°,分别以四边向外做正方形甲、乙、丙、丁,若用S甲、S乙、S丙、S丁来表示它们的面积,那么下列结论正确的是( )
A.S甲= S丁 B.S乙=S丙
C.S甲+S乙=S丙+S丁 D.S甲-S乙=S丙-S丁
10.如图,在Rt△ABC中,∠C=90°,D,E分别为CA,CB的中点,BF平分∠ABC,交DE于点F,若AC=2,BC=4,则DF的长为( )
A.0.5 B.1 C.1.5 D.2
二、填空题
1、一颗大树在一次强烈的地震中于离树根B处8米的C处折断倒下(如图),树顶A落在离树根B处6米,则大树的原长为 ______ 米.
2、我国古代数学著作《九章算术》中有这样一个问题:“今有池方一丈,葭(jiā)生其中央,出水一尺,引葭赴岸,适与岸齐问水深几何?”(注:丈、尺是长度单位,1丈=10尺)这段话翻译成现代汉语,即为:如图,有一个水池,水面是一个边长为1丈的正方形,在水池正中央有一根芦苇,它高出水面1尺,如果把这根芦苇拉向水池一边的中点,它的顶端恰好到达池边的水面.则水池里水的深度是_______________尺.
3、如图,矩形ABCD中,,,E,F,Q分别是AD和BC、DC的中点,P是EF上的点,则的最小值为________.
4、如图,在中,,将线段绕点顺时针旋转至,过点作,垂足为,若,,则的长为__.
5、如图,AB⊥BC,CD⊥BC,垂足分别为B,C,P为线段BC上一点,连结PA,PD.已知AB=5,DC=4,BC=12,则AP+DP的最小值为_____.
6.一根直立于水中的芦节(BD)高出水面(AC)2米,一阵风吹来,芦苇的顶端D恰好到达水面的C处,且C到BD的距离AC=6米,水的深度(AB)为 米
三、解答题
1.如图,在和中,AB为斜边,AC=BD,BC、AD相交于点E
(1)请说明AE=BE的理由;
(2)若∠AEC=45°,AC=1,求CB的长.
2、如图和都是等腰直角三角形,,,顶点在的斜边上,求证:.
3、如图,在四边形ABCD中,∠B=∠D=90°,∠C=60°,AD=1,BC=2,求AB、CD的长.
4 勾股定理神秘而美妙,它的证法多样,其巧妙各有不同,当两个全等的直角三角形如图摆放时,也可以用面积法来证明勾股定理,请完成证明过程.
5 如图,将三角形纸片折叠,使点,都与点重合,折痕分别为,已知,,,求的长.
2.观察、思考与验证
(1)如图1是一个重要公式的几何解释,请你写出这个公式 .
(2)如图2所示,∠B=∠D=90°,且B,C,D在同一直线上.试说明:∠ACE=90°.
(3)伽菲尔德(1881年任美国第20届总统)利用(1)中的公式和图2证明了勾股定理(发表在1876年4月1日的<新英格兰教育日志》上),请你写出验证过程.
