圆周角
图片预览



文档简介
课件15张PPT。华师大九年级数学(下)第23章 圆23.1.3. 圆周角和圆心角的关系
-圆周角定理探究活动:有关圆周角的度数 1. 探究半圆或直径所对的圆周角 等于多少度? 2.90°的圆周角所对的弦是否是直径?线段AB是⊙O的直径,点C是⊙O上任意一点(除点A、B), 那 么,∠ACB就是直径AB所对的圆周角.想想看,∠ACB会是怎么样的角?为什么呢?证明:
因为OA=OB=OC,所以△AOC、△BOC都是等腰三角形,所以∠OAC=∠OCA,∠OBC=∠OCB. 又 ∠OAC+∠OBC+∠ACB=180°,所以 ∠ACB=∠OCA+∠OCB=90°.因此,不管点C在⊙O上何处(除点A、B),∠ACB总等于90°,即:
结论:
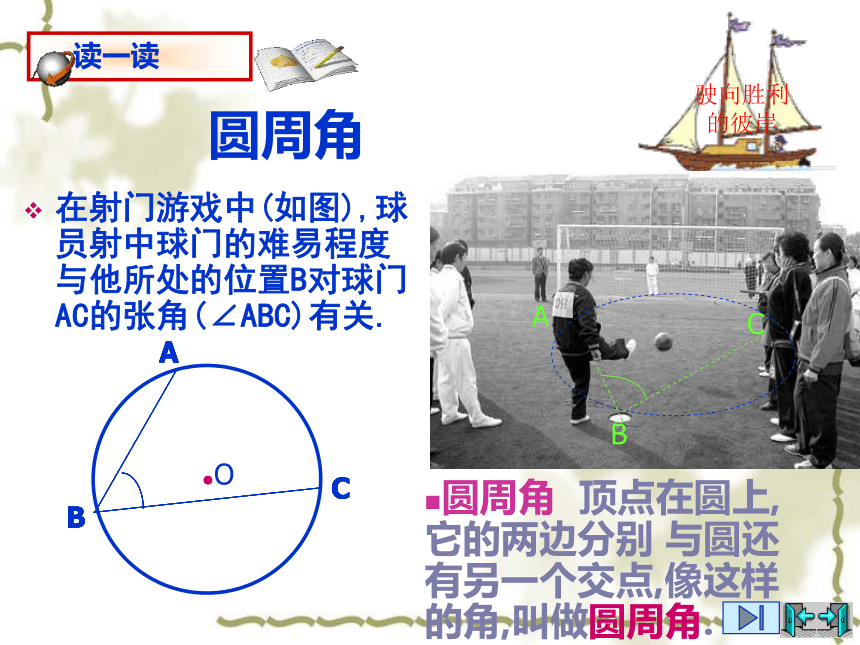
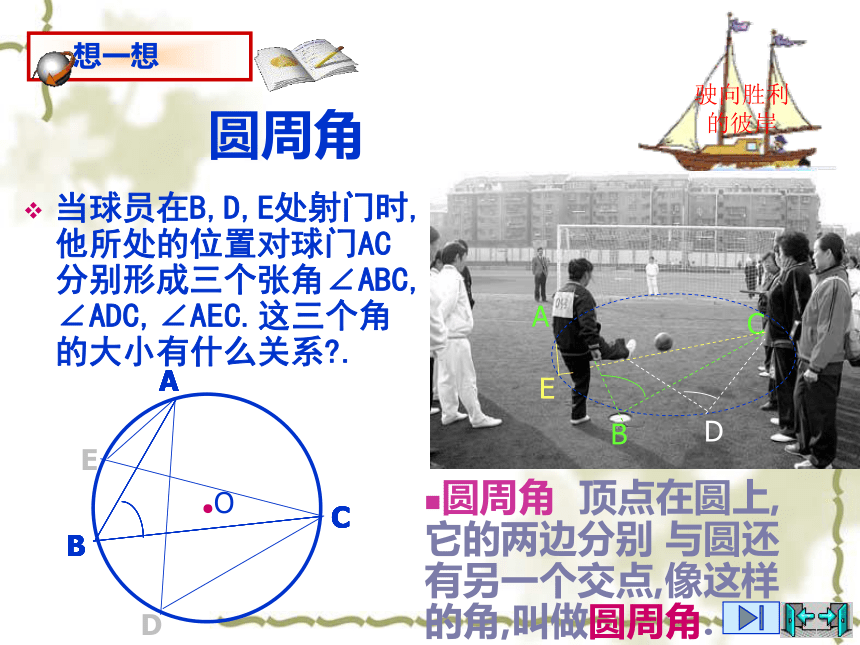
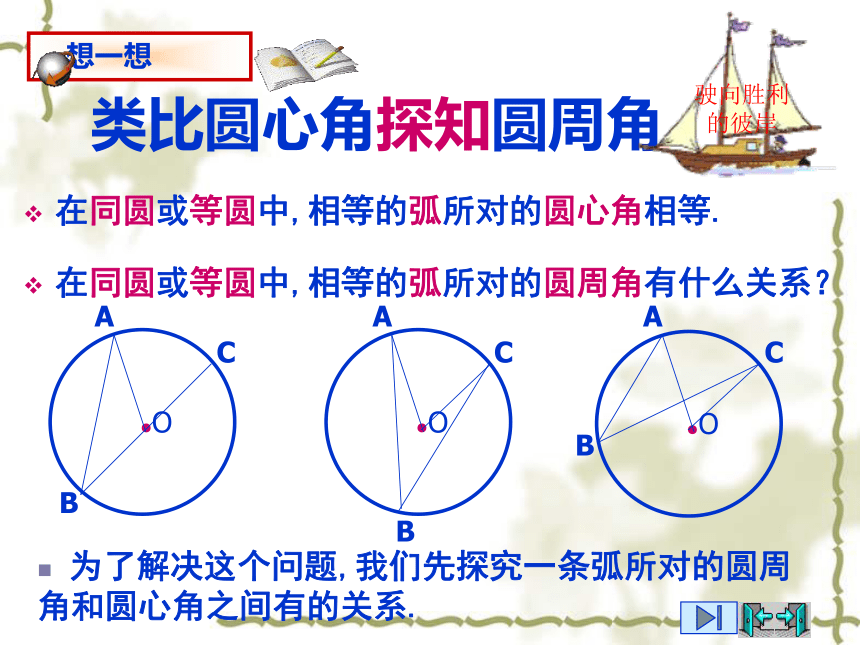
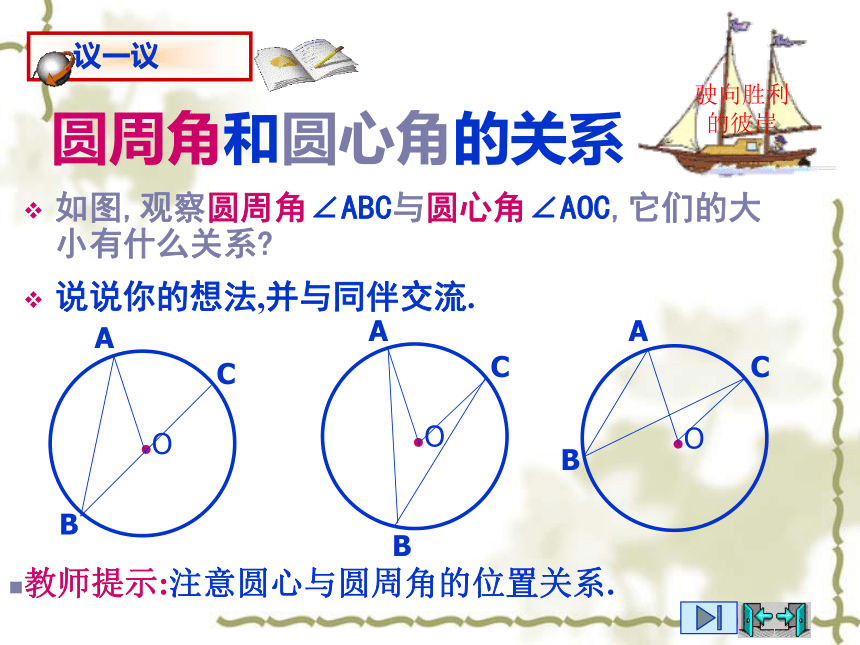
半圆或直径所对的圆周角都相等,都等于90°(直角)。反过来也是成立的,即90°的圆周角所对的弦是圆的直径圆周角在射门游戏中(如图),球员射中球门的难易程度与他所处的位置B对球门AC的张角(∠ABC)有关.圆周角 顶点在圆上,它的两边分别 与圆还有另一个交点,像这样的角,叫做圆周角.圆周角当球员在B,D,E处射门时,他所处的位置对球门AC分别形成三个张角∠ABC, ∠ADC,∠AEC.这三个角的大小有什么关系?.圆周角 顶点在圆上,它的两边分别 与圆还有另一个交点,像这样的角,叫做圆周角.类比圆心角探知圆周角在同圆或等圆中,相等的弧所对的圆心角相等.在同圆或等圆中,相等的弧所对的圆周角有什么关系? 为了解决这个问题,我们先探究一条弧所对的圆周角和圆心角之间有的关系.圆周角和圆心角的关系如图,观察圆周角∠ABC与圆心角∠AOC,它们的大小有什么关系?说说你的想法,并与同伴交流.教师提示:注意圆心与圆周角的位置关系.圆周角和圆心角的关系1.首先考虑一种特殊情况:
当圆心(O)在圆周角(∠ABC)的一边(BC)上时,圆周角∠ABC与圆心角∠AOC的大小关系.∵∠AOC是△ABO的外角,∴∠AOC=∠B+∠A.∵OA=OB,∴∠A=∠B.∴∠AOC=2∠B.你能写出这个命题吗?一条弧所对的圆周角等于它所对的圆心角的一半.老师期望:你可要理解并掌握这个模型.圆周角和圆心角的关系如果圆心不在圆周角的一边上,结果会怎样?
2.当圆心(O)在圆周角(∠ABC)的内部时,圆周角∠ABC与圆心角∠AOC的大小关系会怎样?老师提示:能否转化为1的情况?过点B作直径BD.由1可得:你能写出这个命题吗?一条弧所对的圆周角等于它所对的圆心角的一半.圆周角和圆心角的关系如果圆心不在圆周角的一边上,结果会怎样?
3.当圆心(O)在圆周角(∠ABC)的外部时,圆周角∠ABC与圆心角∠AOC的大小关系会怎样?老师提示:能否也转化为1的情况?过点B作直径BD.由1可得:你能写出这个命题吗?一条弧所对的圆周角等于它所对的圆心角的一半.圆周角定理综上所述,圆周角∠ABC与圆心角∠AOC的大小关系是:圆周角定理 一条弧所对的圆周角等于它所对的圆心角的一半.老师提示:圆周角定理是承上启下的知识点,要予以重视.思考与巩固1.如图,在⊙O中,∠BOC=50°,求∠A的大小. 2.举出生活中含有圆周角的例子.拓展 化心动为行动1.如图(1),在⊙O中,∠BAC=50°,求∠C的大小.2.如图(2),在⊙O中,∠B,∠D,∠E的大小有什么关系?为什么?
3.如图(3),AB是直径,你能确定∠C的度数吗?挑战自我 祝你成功!P52 6,7
P74 3结束寄语要养成用数学的语言去说明道理,用数学的思维去解读世界的习惯.再见
-圆周角定理探究活动:有关圆周角的度数 1. 探究半圆或直径所对的圆周角 等于多少度? 2.90°的圆周角所对的弦是否是直径?线段AB是⊙O的直径,点C是⊙O上任意一点(除点A、B), 那 么,∠ACB就是直径AB所对的圆周角.想想看,∠ACB会是怎么样的角?为什么呢?证明:
因为OA=OB=OC,所以△AOC、△BOC都是等腰三角形,所以∠OAC=∠OCA,∠OBC=∠OCB. 又 ∠OAC+∠OBC+∠ACB=180°,所以 ∠ACB=∠OCA+∠OCB=90°.因此,不管点C在⊙O上何处(除点A、B),∠ACB总等于90°,即:
结论:
半圆或直径所对的圆周角都相等,都等于90°(直角)。反过来也是成立的,即90°的圆周角所对的弦是圆的直径圆周角在射门游戏中(如图),球员射中球门的难易程度与他所处的位置B对球门AC的张角(∠ABC)有关.圆周角 顶点在圆上,它的两边分别 与圆还有另一个交点,像这样的角,叫做圆周角.圆周角当球员在B,D,E处射门时,他所处的位置对球门AC分别形成三个张角∠ABC, ∠ADC,∠AEC.这三个角的大小有什么关系?.圆周角 顶点在圆上,它的两边分别 与圆还有另一个交点,像这样的角,叫做圆周角.类比圆心角探知圆周角在同圆或等圆中,相等的弧所对的圆心角相等.在同圆或等圆中,相等的弧所对的圆周角有什么关系? 为了解决这个问题,我们先探究一条弧所对的圆周角和圆心角之间有的关系.圆周角和圆心角的关系如图,观察圆周角∠ABC与圆心角∠AOC,它们的大小有什么关系?说说你的想法,并与同伴交流.教师提示:注意圆心与圆周角的位置关系.圆周角和圆心角的关系1.首先考虑一种特殊情况:
当圆心(O)在圆周角(∠ABC)的一边(BC)上时,圆周角∠ABC与圆心角∠AOC的大小关系.∵∠AOC是△ABO的外角,∴∠AOC=∠B+∠A.∵OA=OB,∴∠A=∠B.∴∠AOC=2∠B.你能写出这个命题吗?一条弧所对的圆周角等于它所对的圆心角的一半.老师期望:你可要理解并掌握这个模型.圆周角和圆心角的关系如果圆心不在圆周角的一边上,结果会怎样?
2.当圆心(O)在圆周角(∠ABC)的内部时,圆周角∠ABC与圆心角∠AOC的大小关系会怎样?老师提示:能否转化为1的情况?过点B作直径BD.由1可得:你能写出这个命题吗?一条弧所对的圆周角等于它所对的圆心角的一半.圆周角和圆心角的关系如果圆心不在圆周角的一边上,结果会怎样?
3.当圆心(O)在圆周角(∠ABC)的外部时,圆周角∠ABC与圆心角∠AOC的大小关系会怎样?老师提示:能否也转化为1的情况?过点B作直径BD.由1可得:你能写出这个命题吗?一条弧所对的圆周角等于它所对的圆心角的一半.圆周角定理综上所述,圆周角∠ABC与圆心角∠AOC的大小关系是:圆周角定理 一条弧所对的圆周角等于它所对的圆心角的一半.老师提示:圆周角定理是承上启下的知识点,要予以重视.思考与巩固1.如图,在⊙O中,∠BOC=50°,求∠A的大小. 2.举出生活中含有圆周角的例子.拓展 化心动为行动1.如图(1),在⊙O中,∠BAC=50°,求∠C的大小.2.如图(2),在⊙O中,∠B,∠D,∠E的大小有什么关系?为什么?
3.如图(3),AB是直径,你能确定∠C的度数吗?挑战自我 祝你成功!P52 6,7
P74 3结束寄语要养成用数学的语言去说明道理,用数学的思维去解读世界的习惯.再见
