8.6.3平面与平面垂直(第2课时) 课件(共18张PPT)
文档属性
| 名称 | 8.6.3平面与平面垂直(第2课时) 课件(共18张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 549.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-14 08:25:42 | ||
图片预览





文档简介
(共18张PPT)
8.6.3平面与平面垂直
(第2课时)
1.以二面角的棱上任意一点为顶点,在两个面内分别作垂直于棱的两条射线,这两条射线所成的角叫做二面角的平面角.
2.一般地,两个平面相交,如果它们所成的二面角是直二面角,就说这两个平面互相垂直.
3.面面垂直的判定定理:如果一个平面经过另一个平面的垂线,则这两个平面垂直.
O
A
B
β
α
l
m
复习引入
如图,已知平面α⊥平面β, α∩β=a,则β内异于a的直线b与a是什么位置关系?相应地,b与α是什么位置关系?
因为b与a在同一平面内,
故可能平行,也可能相交
b//a → b//α
b与a相交 → b与α相交
思考:教室内的黑板所在的平面与地面所在的平面垂直,在黑板上任意画一条直线与地面垂直吗 怎样画才能保证所画直线与地面垂直
创设情境
思考:当平面α⊥平面β时, β内什么样的直线b与α垂直?
你能将上述结论用符号语言表述出来,并对其进行证明吗?
猜想:b⊥a → b⊥α.
符号语言:
设b∩a=A,在α内过点A作直线c⊥a,则直线b,c所成的角就是二面角α-a-β的平面角.
又因为b⊥a,a∩c=A,
所以b⊥α.
证明:
由α⊥β,故b⊥c.
新知探索
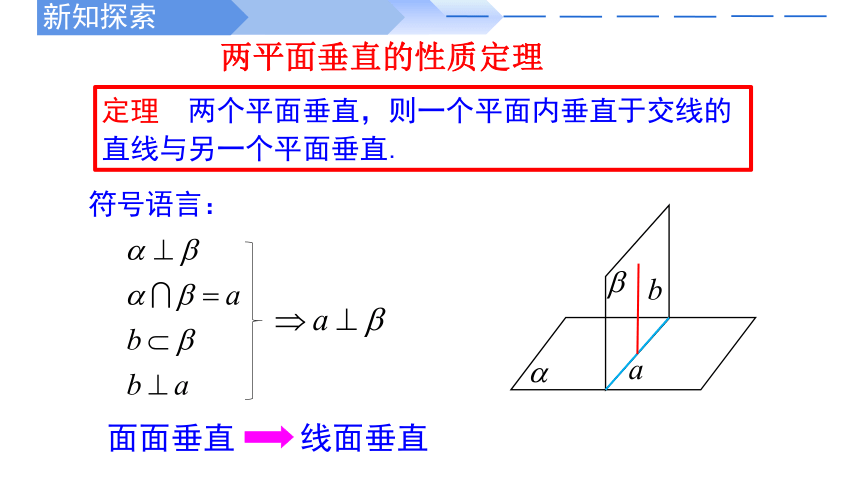
定理 两个平面垂直,则一个平面内垂直于交线的直线与另一个平面垂直.
两平面垂直的性质定理
面面垂直 线面垂直
符号语言:
新知探索
思考:设平面α⊥平面β,点P在平面α内,过点P作平面β的垂线a,则直线a与平面α具有什么位置关系?
所以直线a与直线b重合,因此a .
证明:设α∩β=c.
过点P在平面α内作直线b⊥c.
由平面与平面垂直的性质定理可知,b⊥β.
因为过一点有且仅有一条直线与平面β垂直
a在平面α内
新知探索
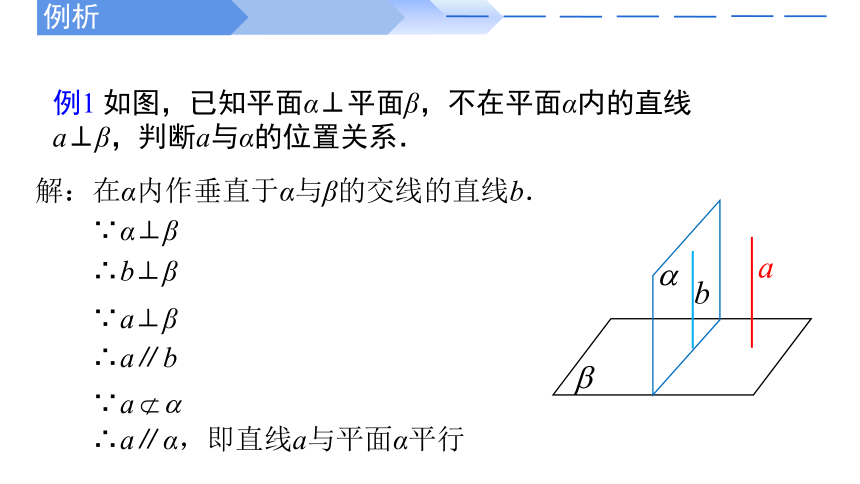
例1 如图,已知平面α⊥平面β,不在平面α内的直线a⊥β,判断a与α的位置关系.
解:在α内作垂直于α与β的交线的直线b.
∵α⊥β
∴b⊥β
∵a⊥β
∴a∥b
∵a
∴a∥α,即直线a与平面α平行
例析
例2 如图,已知PA⊥平面ABC,平面PAB ⊥平面PBC.
求证:BC⊥平面PAB.
P
A
B
C
证明:过点A作AE⊥PB,垂足为E.
∵平面PAB⊥平面PBC,
平面PAB∩平面PBC=PB,
∴AE⊥平面PBC.
∵BC 平面PBC,∴AE⊥BC.
又∵PA⊥平面ABC,BC 平面ABC,
∴PA⊥BC.
又PA∩AE=A,∴BC⊥平面PAB.
例析
√
×
×
(4)过一个平面内任意一点作交线的垂线,则此垂线必垂直于另一个平面.
√
小练
例2 如图所示,P是四边形ABCD所在平面外的一点,四边形ABC是边长为a的菱形且∠DAB=60°,侧面PAD为正三角形,其所在平面垂直于底面ABCD.
(1)若G为AD的中点,求证:BG⊥平面PAD;
(2)求证:AD⊥PB.
(1)连接BD,菱形ABCD,∠DAB=60° △ABD为正三角形
BG⊥AD 由平面与平面垂直的性质定理得出结论
(2)连接PG,要证AD⊥PB,只需证AD⊥平面PBG即可.
例析
(1)如图,在菱形ABCD中,连接BD,
∵∠DAB=60°,∴△ABD为正三角形,
∵G是AD的中点,∴BG⊥AD.
∵平面PAD⊥平面ABCD,
且平面PAD∩平面ABCD=AD,∴BG⊥平面PAD.
(2)如图,连接PG.
∵△PAD是正三角形,G是AD的中点,
∴PG⊥AD,由(1)知BG⊥AD.又∵PG∩BG=G.
∴AD⊥平面PBG.而PB 平面PBG,∴AD⊥PB.
证明:
例析
1.在平面四边形ABCD中, 已知AB=BC=CD=a, ∠ABC=90°,∠BCD=135°, 沿AC将四边形折成直二面角B-AC -D.
(1)求证: 平面ABC⊥平面BCD.
(2)求平面ABD与平面ACD所成的角的度数.
解:(1)在四边形ABCD中,∵AB=BC,AB⊥BC,
∴∠ACB=45°,
而∠BCD=∠ACB+∠ACD=135°,
∴∠ACD=90°,即CD⊥AC.
又平面ABC⊥平面ACD,且平面ABC∩平面ACD=AC,
∴CD⊥平面ABC,又CD 平面BCD,
∴平面ABC⊥平面BCD.
巩固练习
(2)过点B作BE⊥AC交AC于E,又过点E在平面ACD内作EF⊥AD交AD于F,连接BF.
∵平面ABC⊥平面ACD,且平面ABC∩平面ACD=AC,
∴BE⊥平面ACD,∴BE⊥AD
又EF⊥AD,且EF∩BE=E,∴AD⊥平面BEF
∴BF⊥AD,故∠BFE是二面角B-AD-C的平面角.
故平面ABD与平面ACD所成的角的度数为60°.
∴∠BFE=60°,
又sin∠DAC= =sin∠EAF,
∴AE= AC= a.
∵E为AC的中点,
∴tan∠BFE=
∴在Rt ABC中,EF=AE·sin∠EAF= a
新知探索
题型二 平面与平面平行性质定理的应用
例4.如图所示,两条异面直线BA,DC与两平行平面α,β分别交于点B,A和D,C,点M,N分别是AB,CD的中点,求证:MN∥平面α.
【解答】如图,过点A作AE∥CD交α于点E,取AE的中点P,连接MP,PN,BE,ED,BD,AC.
因为AE∥CD,所以AE,CD确定平面AEDC.
则平面AEDC∩α=DE,平面AEDC∩β=AC,因为α∥β,所以AC∥DE.
练习巩固
又P,N分别为AE,CD的中点,
所以PN∥DE,PN α,DE α,所以PN∥α.
又M,P分别为AB,AE的中点,
所以MP∥BE,且MP α,BE α.
所以MP∥α,因为MP∩PN=P,
所以平面MPN∥α.
又MN 平面MPN,所以MN∥平面α.
例析
应用平面与平面平行性质定理的基本步骤
解题技巧
面面平行性质定理的实质:面面平行 线线平行,体现了转化思想.与判定定理交替使用,可实现线面、线线、面面平行间的相互转化.
例析
变1:如图,在三棱锥P-ABC中,D,E,F分别是PA,PB,PC的中点,M是AB上一点,连接MC,N是PM与DE的交点,连接NF.求证:NF∥CM.
【解答】因为D,E,F分别为PA,PB,PC的中点,所以DE∥AB,
又DE 平面ABC,AB 平面ABC,所以DE∥平面ABC,
同理EF∥平面ABC,又DE∩EF=E,所以平面DEF∥平面ABC,
又平面PMC∩平面ABC=MC,平面PMC∩平面DEF=NF,由面面平行的性质定理得,NF∥MC.
例析
平面与平面垂直
二面角
面面垂直的定义
面面垂直的判定定理
面面垂直的性质定理
课堂小结
8.6.3平面与平面垂直
(第2课时)
1.以二面角的棱上任意一点为顶点,在两个面内分别作垂直于棱的两条射线,这两条射线所成的角叫做二面角的平面角.
2.一般地,两个平面相交,如果它们所成的二面角是直二面角,就说这两个平面互相垂直.
3.面面垂直的判定定理:如果一个平面经过另一个平面的垂线,则这两个平面垂直.
O
A
B
β
α
l
m
复习引入
如图,已知平面α⊥平面β, α∩β=a,则β内异于a的直线b与a是什么位置关系?相应地,b与α是什么位置关系?
因为b与a在同一平面内,
故可能平行,也可能相交
b//a → b//α
b与a相交 → b与α相交
思考:教室内的黑板所在的平面与地面所在的平面垂直,在黑板上任意画一条直线与地面垂直吗 怎样画才能保证所画直线与地面垂直
创设情境
思考:当平面α⊥平面β时, β内什么样的直线b与α垂直?
你能将上述结论用符号语言表述出来,并对其进行证明吗?
猜想:b⊥a → b⊥α.
符号语言:
设b∩a=A,在α内过点A作直线c⊥a,则直线b,c所成的角就是二面角α-a-β的平面角.
又因为b⊥a,a∩c=A,
所以b⊥α.
证明:
由α⊥β,故b⊥c.
新知探索
定理 两个平面垂直,则一个平面内垂直于交线的直线与另一个平面垂直.
两平面垂直的性质定理
面面垂直 线面垂直
符号语言:
新知探索
思考:设平面α⊥平面β,点P在平面α内,过点P作平面β的垂线a,则直线a与平面α具有什么位置关系?
所以直线a与直线b重合,因此a .
证明:设α∩β=c.
过点P在平面α内作直线b⊥c.
由平面与平面垂直的性质定理可知,b⊥β.
因为过一点有且仅有一条直线与平面β垂直
a在平面α内
新知探索
例1 如图,已知平面α⊥平面β,不在平面α内的直线a⊥β,判断a与α的位置关系.
解:在α内作垂直于α与β的交线的直线b.
∵α⊥β
∴b⊥β
∵a⊥β
∴a∥b
∵a
∴a∥α,即直线a与平面α平行
例析
例2 如图,已知PA⊥平面ABC,平面PAB ⊥平面PBC.
求证:BC⊥平面PAB.
P
A
B
C
证明:过点A作AE⊥PB,垂足为E.
∵平面PAB⊥平面PBC,
平面PAB∩平面PBC=PB,
∴AE⊥平面PBC.
∵BC 平面PBC,∴AE⊥BC.
又∵PA⊥平面ABC,BC 平面ABC,
∴PA⊥BC.
又PA∩AE=A,∴BC⊥平面PAB.
例析
√
×
×
(4)过一个平面内任意一点作交线的垂线,则此垂线必垂直于另一个平面.
√
小练
例2 如图所示,P是四边形ABCD所在平面外的一点,四边形ABC是边长为a的菱形且∠DAB=60°,侧面PAD为正三角形,其所在平面垂直于底面ABCD.
(1)若G为AD的中点,求证:BG⊥平面PAD;
(2)求证:AD⊥PB.
(1)连接BD,菱形ABCD,∠DAB=60° △ABD为正三角形
BG⊥AD 由平面与平面垂直的性质定理得出结论
(2)连接PG,要证AD⊥PB,只需证AD⊥平面PBG即可.
例析
(1)如图,在菱形ABCD中,连接BD,
∵∠DAB=60°,∴△ABD为正三角形,
∵G是AD的中点,∴BG⊥AD.
∵平面PAD⊥平面ABCD,
且平面PAD∩平面ABCD=AD,∴BG⊥平面PAD.
(2)如图,连接PG.
∵△PAD是正三角形,G是AD的中点,
∴PG⊥AD,由(1)知BG⊥AD.又∵PG∩BG=G.
∴AD⊥平面PBG.而PB 平面PBG,∴AD⊥PB.
证明:
例析
1.在平面四边形ABCD中, 已知AB=BC=CD=a, ∠ABC=90°,∠BCD=135°, 沿AC将四边形折成直二面角B-AC -D.
(1)求证: 平面ABC⊥平面BCD.
(2)求平面ABD与平面ACD所成的角的度数.
解:(1)在四边形ABCD中,∵AB=BC,AB⊥BC,
∴∠ACB=45°,
而∠BCD=∠ACB+∠ACD=135°,
∴∠ACD=90°,即CD⊥AC.
又平面ABC⊥平面ACD,且平面ABC∩平面ACD=AC,
∴CD⊥平面ABC,又CD 平面BCD,
∴平面ABC⊥平面BCD.
巩固练习
(2)过点B作BE⊥AC交AC于E,又过点E在平面ACD内作EF⊥AD交AD于F,连接BF.
∵平面ABC⊥平面ACD,且平面ABC∩平面ACD=AC,
∴BE⊥平面ACD,∴BE⊥AD
又EF⊥AD,且EF∩BE=E,∴AD⊥平面BEF
∴BF⊥AD,故∠BFE是二面角B-AD-C的平面角.
故平面ABD与平面ACD所成的角的度数为60°.
∴∠BFE=60°,
又sin∠DAC= =sin∠EAF,
∴AE= AC= a.
∵E为AC的中点,
∴tan∠BFE=
∴在Rt ABC中,EF=AE·sin∠EAF= a
新知探索
题型二 平面与平面平行性质定理的应用
例4.如图所示,两条异面直线BA,DC与两平行平面α,β分别交于点B,A和D,C,点M,N分别是AB,CD的中点,求证:MN∥平面α.
【解答】如图,过点A作AE∥CD交α于点E,取AE的中点P,连接MP,PN,BE,ED,BD,AC.
因为AE∥CD,所以AE,CD确定平面AEDC.
则平面AEDC∩α=DE,平面AEDC∩β=AC,因为α∥β,所以AC∥DE.
练习巩固
又P,N分别为AE,CD的中点,
所以PN∥DE,PN α,DE α,所以PN∥α.
又M,P分别为AB,AE的中点,
所以MP∥BE,且MP α,BE α.
所以MP∥α,因为MP∩PN=P,
所以平面MPN∥α.
又MN 平面MPN,所以MN∥平面α.
例析
应用平面与平面平行性质定理的基本步骤
解题技巧
面面平行性质定理的实质:面面平行 线线平行,体现了转化思想.与判定定理交替使用,可实现线面、线线、面面平行间的相互转化.
例析
变1:如图,在三棱锥P-ABC中,D,E,F分别是PA,PB,PC的中点,M是AB上一点,连接MC,N是PM与DE的交点,连接NF.求证:NF∥CM.
【解答】因为D,E,F分别为PA,PB,PC的中点,所以DE∥AB,
又DE 平面ABC,AB 平面ABC,所以DE∥平面ABC,
同理EF∥平面ABC,又DE∩EF=E,所以平面DEF∥平面ABC,
又平面PMC∩平面ABC=MC,平面PMC∩平面DEF=NF,由面面平行的性质定理得,NF∥MC.
例析
平面与平面垂直
二面角
面面垂直的定义
面面垂直的判定定理
面面垂直的性质定理
课堂小结
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
