8.3.2圆柱、圆锥、圆台、球表面积和体积 课件(共58张PPT)
文档属性
| 名称 | 8.3.2圆柱、圆锥、圆台、球表面积和体积 课件(共58张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 6.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-14 08:27:11 | ||
图片预览






文档简介
8.3.2 圆柱、圆锥、圆台和圆
的表面积与体积
l
O
O'
2πr
r
2πr
O
S
l
r
O'
O
r'
2πr'
r
l
2πr
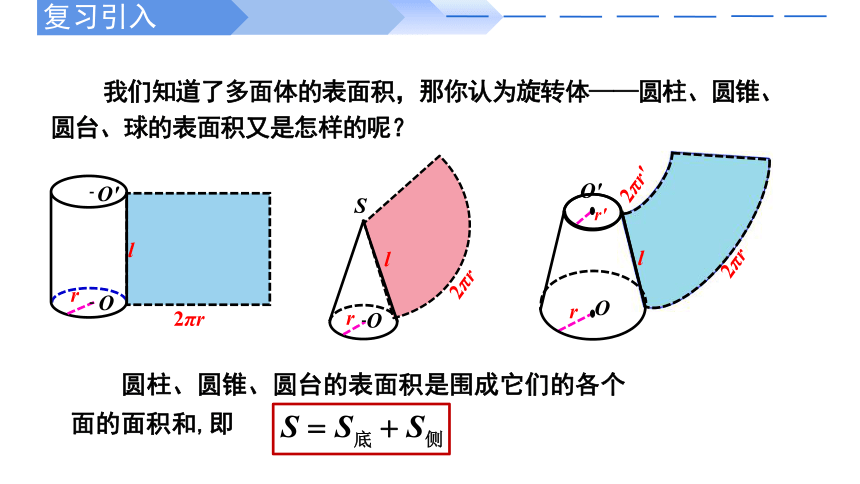
我们知道了多面体的表面积,那你认为旋转体——圆柱、圆锥、圆台、球的表面积又是怎样的呢?
圆柱、圆锥、圆台的表面积是围成它们的各个面的面积和,即
复习引入
一、圆柱的表面积
l
O
O'
2πr
r
新知探索
2πr
O
S
l
r
二、圆锥的表面积
新知探索
O'
O
r'
2πr'
r
l
2πr
l'
三、圆台的表面积
l
新知探索
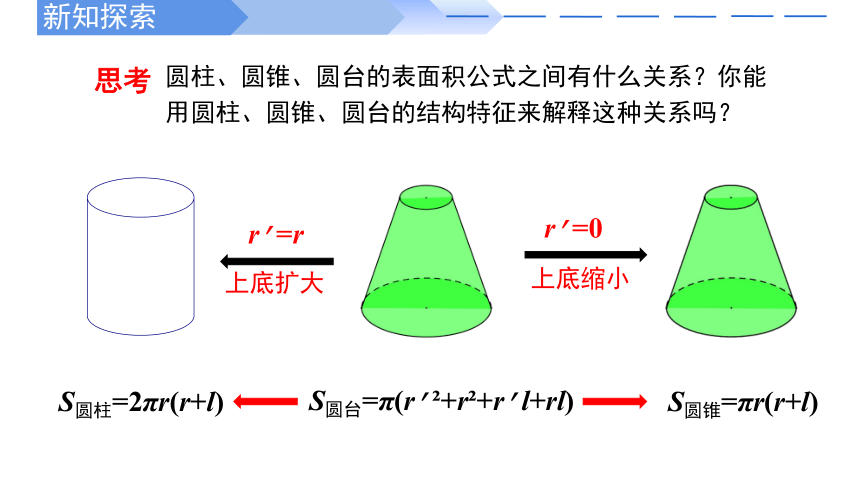
圆柱、圆锥、圆台的表面积公式之间有什么关系?你能用圆柱、圆锥、圆台的结构特征来解释这种关系吗?
r’=r
r’=0
上底扩大
上底缩小
S圆台=π(r’?+r?+r’l+rl)
S圆柱=2πr(r+l)
S圆锥=πr(r+l)
思考
新知探索
高h
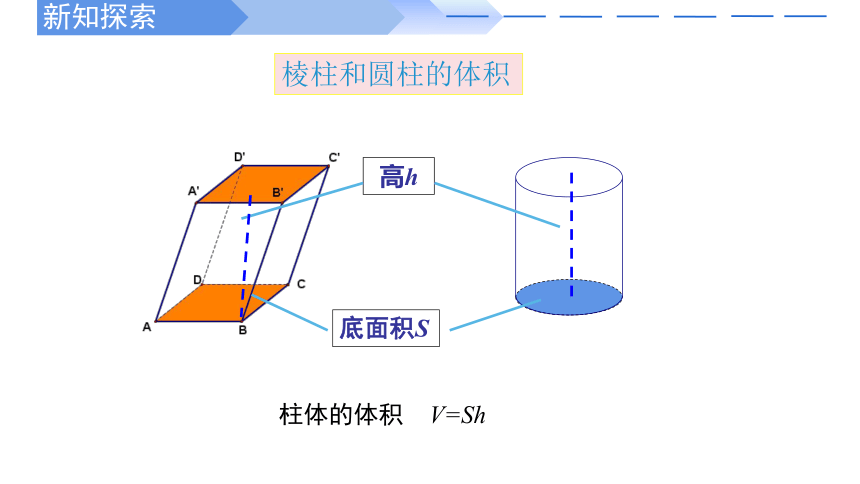
柱体的体积 V=Sh
底面积S
棱柱和圆柱的体积
新知探索
A
B
C
D
E
O
S
底面积S
高h
棱锥和圆锥的体积
锥体的体积
新知探索
高h
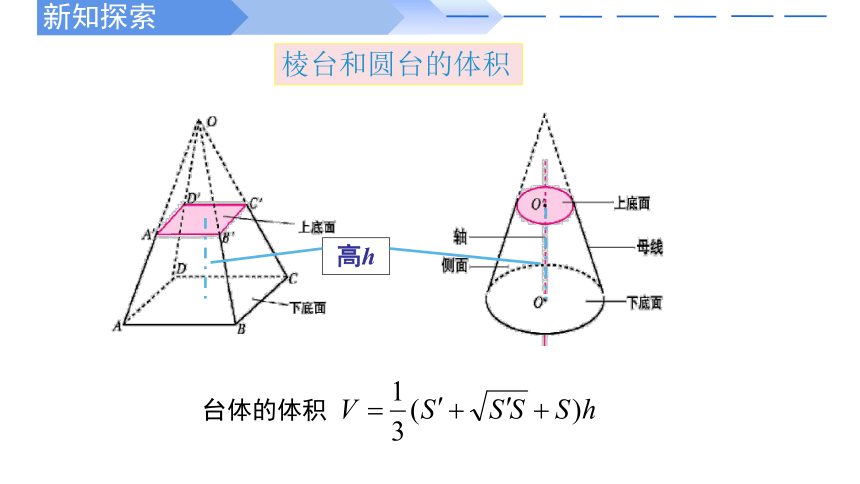
棱台和圆台的体积
台体的体积
新知探索
l
O
O'
r
O
S
l
r
h
h
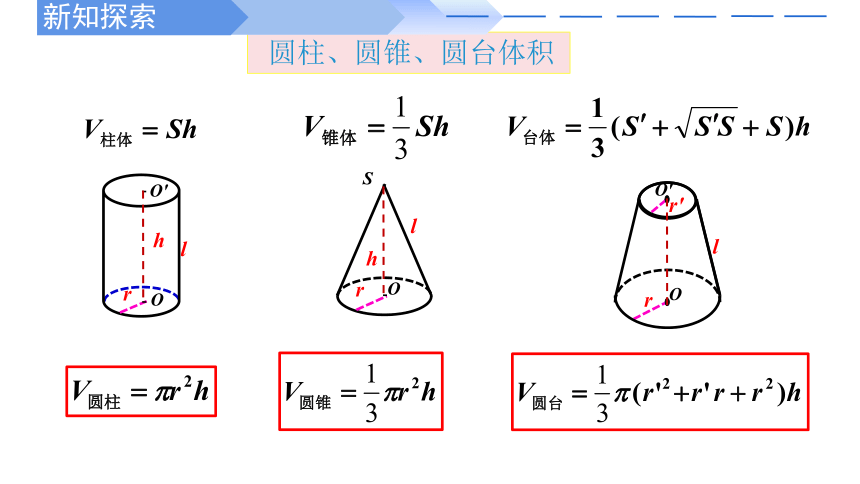
圆柱、圆锥、圆台体积
O'
O
r'
r
l
新知探索
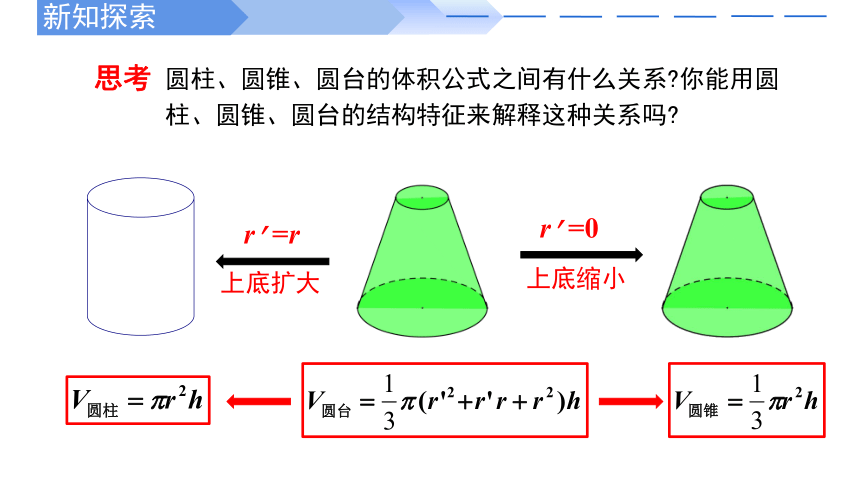
圆柱、圆锥、圆台的体积公式之间有什么关系?你能用圆柱、圆锥、圆台的结构特征来解释这种关系吗?
r’=r
r’=0
上底扩大
上底缩小
思考
新知探索
新知探索
辨析1:判断正误.
1.圆锥的侧面展开图为扇形,其中扇形的弧长为圆锥底面圆的周长.( )
2.若圆柱的底面圆的直径与圆柱的高相等,则圆柱的侧面展开图是正方形. ( )
答案:√,×.
辨析2:若圆柱的底面半径为1,母线长为2,则它的侧面积为( ).
A.2???? B.3???? C.???? D.4????
?
答案:D.
割圆术
早在公元三世纪,我国数学家刘徽为推导圆的面积公式而发明了“倍边法割圆术”.他用加倍的方式不断增加圆内接正多边形的边数,使其面积与圆的面积之差更小,即所谓“割之弥细,所失弥小”.这样重复下去,就达到了“割之又割,以至于不可再割,则与圆合体而无所失矣”.这是世界上最早的“极限”思想.
新知探索
????球=????????????????
?
把一个半径为R的球的上半球横向切成n(无穷大)份, 每份等高并且把每份看成一个类似圆台,球的表面积为所有圆台的侧面积之和.
A
O
球体由n个这样的形状组成
球的表面积是大圆面积的4倍
新知探索
思考:在小学,我们学习了圆的面积公式,你还记得是如何求得的吗?类比这种方法,你能由球的表面积公式推导出球的体积公式吗?
如图,把球O的表面分成n个小网格,连接球心O和每个小网格的顶点,整个球体就被分割成n个“小锥体”.
O
A
B
C
D
O
A
B
C
D
当n越大,每个小网格越小时,每个“小锥体”的底面就越平,“小锥体”就越近似于棱锥,其高越近似于球半径R,设O-ABCD是其中一个“小锥体”,它的体积是
新知探索
思考:在小学,我们学习了圆的面积公式,你还记得是如何求得的吗?类比这种方法,你能由球的表面积公式推导出球的体积公式吗?
O
A
B
C
D
O
A
B
C
D
由于球的体积就是这n个“小锥体”的体积之和,而这n个“小锥体”的底面积之和就是球的表面积.因此,球的体积
由此,我们得到球的体积公式
新知探索
例1 如右图,某种浮标由两个半球和一个圆柱黏合而成,半球的直径是0.3m,圆柱高0.6m.如果在 浮标表面涂一层防水漆,每平方米需要0.5kg涂料,那么给1000个这样的浮标涂防水漆需要多少涂料?(π取3.14)
解:一个浮标的表面积为
2π×0.15×0.6 + 4π×0.152 =0.8478(m2)
所以给1000个这样的浮标涂防水漆约需涂料
0.8478×0.5×1000 =423.9(kg).
例析
例2 如右图,圆柱的底面直径和高都等于球的直径, 求球与圆柱的体积之比.
O
R
解:(1)设球的半径为R,则圆柱的底面半径为R,高为2R.
问题:球的表面积与圆柱的侧面积之比呢?
例析
练习
题型一:圆柱、圆锥、圆台的表面积
例1.(1)已知圆柱的上、下底面的中心分别为????1,????2,过直线????1????2的平面截该圆柱所得的截面是面积为8的正方形,则该圆柱的表面积为( ).
A.122???? B.12???? C.82???? D.10????
?
练习
题型一:圆柱、圆锥、圆台的表面积
例1.(1)已知圆柱的上、下底面的中心分别为????1,????2,过直线????1????2的平面截该圆柱所得的截面是面积为8的正方形,则该圆柱的表面积为( ).
A.122???? B.12???? C.82???? D.10????
?
答案:B.
解:因为过直线????1????2的平面截该圆柱所得的截面是面积为8的正方形,所以圆柱的高为22,底面圆的直径22为,所以该圆柱的表面积为2×????×(2)2+2????×2×22=12????.故选B.
?
练习
例1.(2)已知一个圆锥的轴截面是等边三角形,其面积为3,则这个圆锥的侧面积为_______.
?
答案:2????.
?
解:设母线长为????,由题意得12????????????????????? 60°=3,所以母线长????=2,又底面半径为1,所以侧面积为????×1×2=2????.
?
练习
方法技巧:
圆柱、圆锥、圆台的表面积的求解步骤:
1.得到空间几何体的平面展开图.
2.依次求出各个平面图形的面积.
3.将各平面图形的面积相加.
练习
例1.(2)已知一个圆锥的轴截面是等边三角形,其面积为3,则这个圆锥的侧面积为_______.
?
答案:2????.
?
解:设母线长为????,由题意得12????????????????????? 60°=3,所以母线长????=2,又底面半径为1,所以侧面积为????×1×2=2????.
?
练习
变1.(1)圆柱的一个底面积是????,侧面展开图是一个正方形,那么这个圆柱的侧面积是( ).
A.4???????? B.2???????? C.???????? D.233????????
?
练习
变1.(1)圆柱的一个底面积是????,侧面展开图是一个正方形,那么这个圆柱的侧面积是( ).
A.4???????? B.2???????? C.???????? D.233????????
?
答案:A.
?
解:底面半径是????????,所以正方形的边长是2π????????=2????????,故圆柱的侧面积是(2????????)2=4????????.故选A.
?
练习
变1.(2)轴截面是正三角形的圆锥称作等边圆锥,则等边圆锥的侧面积是底面积的( ).
A.4倍 B.3倍 C.2倍 D.2倍
?
变1.(3)已知圆台的上、下底面半径分别是2,6,且侧面面积等于两底面面积之和,则圆台的表面积是_______.
?
练习
变1.(2)轴截面是正三角形的圆锥称作等边圆锥,则等边圆锥的侧面积是底面积的( ).
A.4倍 B.3倍 C.2倍 D.2倍
?
答案:D.
?
解:由已知得????=2????,????侧????底=????????????????????2=????????=2,故选D.
?
变1.(3)已知圆台的上、下底面半径分别是2,6,且侧面面积等于两底面面积之和,则圆台的表面积是_______.
?
答案:80????.
?
解:设圆台母线长为????,则由题意得????(2+6)????=????×22+????×62,∴8????????=40????,∴????=5,∴????=????×(2+6)×5+????×22+????×62=40????+4????+36????=80????.
?
练习
题型二:圆柱、圆锥、圆台的体积
例2.(1)若一个圆柱与圆锥的高相等,且轴截面面积也相等,则圆柱与圆锥的体积之比是( ).
A.1 B.1:2 C.3:2 D.3:4
?
练习
题型二:圆柱、圆锥、圆台的体积
例2.(1)若一个圆柱与圆锥的高相等,且轴截面面积也相等,则圆柱与圆锥的体积之比是( ).
A.1 B.1:2 C.3:2 D.3:4
?
答案:D.
解:设圆柱、圆锥的高都为?,底面半径分别为????,????,则有12?2?????=2?????,所以????=2????,????圆锥=13????????2?=43????????2?,????圆柱=????????2?,故????圆锥:????圆锥=3:4.故选D.
?
练习
方法技巧:
求圆柱、圆锥、圆台的体积问题,一是要牢记公式,然后观察空间图形的构成,是单一的旋转体,还是组合体;二是注意旋转体的构成,以及圆柱、圆锥、圆台轴截面的性质,从而找出公式中需要的各个量,代入公式计算.
练习
例2.(2)设圆台的高为3,如图,在轴截面中母线????????1与底面直径????????的夹角为60°,轴截面中的一条对角线垂直于腰,则圆台的体积为_____.
?
解:设上、下底面半径,母线长分别为????,????,????.
作????1????⊥????????于点????,则????1????=3,∠????????1????=60°.
又∠????????1????=90°,∴∠????????1????=60°,∴????????=????1???????????????? 60°=3,∴?????????=3.
????????=????1?????????????????60°=33 ,∴????+????=33,∴????=23,????=3,而?=3.
∴????圆台=13?????(????2+????????+????2)=13????×3×[(23)2+23×3+(3)2]=21????.
∴圆台的体积为21????.
?
练习
变2.(1)若圆台上、下底面面积分别是????,4????,侧面积是4????,则这个圆台的体积是( ).
A.233???? B.23 C.736???? D.733????
?
答案:D.
?
解:????1=????,????2=4????,∴????=1,????=2,
????侧=6????=????(????+????)????,∴????=2,∴?=3.
∴????=13????(1+4+2)×3=733????.故选D.
?
练习
变2.(2)若圆锥的轴截面是等腰直角三角形,侧面积是162????,则圆锥的体积是( ).
A.643???? B.1283???? C.64???? D.1282????
?
答案:A.
?
解:设圆锥的底面半径为????,母线长为????.
∵圆锥的轴截面是等腰直角三角形,∴2????=????2+????2,即????=2????.
由题意得,侧面积????侧=?????????????=2????????2=162????,
∴????=4.∴????=42,高?=????2?????2=4.
∴圆锥的体积????=13?????=13????×42×4=643????.故选A.
?
练习
变2.(3)如图,一个底面半径为2的圆柱被一平面所截,截得的几何体的最短和最长母线长分别为2和3,则该几何体的体积为( ).
A.5???? B.6???? C.20???? D.10????
?
答案:D.
?
解:用一个完全相同的几何体把题中几何体补成一个圆柱,如图,则圆柱的体积为????×22×5=20????,故所求几何体的体积为10????.故选D.
?
练习
题型三:与组合体有关的表面积与体积问题
例3.(1)如图,在底面半径为2,母线长为4的圆锥中挖掉一个高为3的内接圆柱,求圆柱的表面积.
?
解:设圆锥的底面半径为????,圆柱的底面半径为????,表面积为????.
则????=????????=2,????????=4,????????=42?22=23.
如图所示,易知?????????????~?????????????,所以????????????????=????????????????,即323=????2,所以????=1,
????底=2????????2=2????,????侧=2??????????=23????.
所以????=????底+????侧=2????+23????=(2+23)????.
所以圆柱的表面积为(2+23)????.
?
练习
例3.(2)如图,在底面半径为2,母线长为4的圆锥中挖掉一个高为3的内接圆柱,求圆柱的体积与圆锥的体积之比.
?
解:由(1)知,圆柱的底面半径为????=1,高?=3,
所以圆柱的体积????1=????????2?=????×12×3=3????.
圆锥的体积????2=13????×22×23=833????.
所以圆柱与圆锥的体积比为3:8.
?
练习
例3.(3)如图,在底面半径为2,母线长为4的圆锥中挖掉一个高为?的内接圆柱,试求圆柱侧面积的最大值.
?
解:设圆锥的底面半径为????,圆柱的底面半径为????,
则????=????????=2,????????=4,????????=42?22=23.
易知?????????????~?????????????,所以????????????????=????????????????,即23??23=????2,
所以?=23?3????,????圆柱侧=2?????????=2????????(23?3????)=?23????????2+43????????,
所以当????=1,?=3时,圆柱的侧面积最大,其最大值为23????.
?
练习
方法技巧:
关于组合体的表面积与体积问题的解题策略
(1)分析结构特征:弄清组合体的组成形式,找准有关简单几何体的关键量.
(2)设计计算方法:根据组成形式,设计计算方法,特别要注意“拼接面”面积的处理,利用“切割”“补形”的方法求体积.
(3)计算求值:根据设计的计算方法求值.
[提醒]组合体分割成规则的几何体求表面积、体积之和(或差),保证不重不漏.
练习
变3.如图所示,一圆柱内挖去一个圆锥,圆锥的顶点是圆柱底面的圆心,圆锥的底面是圆柱的另一个底面.圆柱的母线长为6,底面半径为2.求该组合体的表面积.
?
解:挖去的圆锥的母线长为62+22=210,则圆锥的侧面积等于410????.圆柱的侧面积为2????×2×6=24????,圆柱的一个底面面积为????×22=4????,所以组合体的表面积为410????+24????+4????=(410+28)????.
?
练习
题型一:球的表面积和体积
例1.(1)一个球的表面积是16????,则它的体积是( ).
A.64???? B.643???? C.32???? D.323????
?
答案:D.
解:设球的半径为????,则由题意可知4????????2=16????,故????=2.
所以球的体积????=43????????3=323????.故选D.
?
练习
例1.(2)已知球的体积为5003????,则它的表面积为_____.
?
答案:100????.
?
解:设球的半径为????,由已知得43????????3=5003????,故????=5.
所以球的表面积????=4????????2=4????×52=100????.
?
练习
方法技巧:
1.球的体积与表面积的求法:必须知道半径????或者通过条件能求出半径????,然后代入体积或表面积公式求解.
2.关键要素:半径和球心是球的关键要素,把握住了这两点,计算球的表面积或体积的相关题目也就轻松自如了.
?
练习
变1.(1)若一个球的表面积与其体积在数值上相等,则此球的半径为______.
答案:3.
?
解:设此球的半径为R,则4????????2=43????????3,解得????=3.
?
变2.(2)如果三个球的半径之比是1:2:3,那么最大球的表面积是其余两个球的表面积之和的______倍.
?
答案:95.
?
解:设小球半径为1,则大球的表面积????大=36????,????小+????中=20????,36????20????=95.
?
练习
题型二:球的截面问题
例2.(1)一平面截一球得到直径为25 ????????的圆面,球心到这个平面的距离是2 ????????,则该球的体积是( ).
A.12???? ????????3 B.36???? ????????3 C.646???? ????????3 D.108???? ????????3
?
答案:B.
解:设球心为????,截面圆心为????1,连接????????1,则????????1垂直于截面圆????1,如图所示.在?????????????????1????中,????1????=5 ????????,????????1=2 ????????,
∴球的半径????=????????=22+(5)2=3(????????),
∴球的体积????=43????×33=36????(????????3).故选B.
?
练习
例2.(2)已知一个球内有相距9 ????????的两个平行截面,它们的面积分别为49???? ????????2和400???? ????????2,则球的表面积是_____????????2.
?
答案:2500????.
?
解:当截面在球心的同侧时,如图①所示为球的轴截面,由球的截面性质知????????1//????????2,且????1,????2为两截面圆的圆心,则????????1⊥????????1,
????????2⊥????????2.设球的半径为????,
∵?????????2????2=49????,∴????2????=7 ????????.
同理,得????1????=20 ????????.
设????????1=???? ????????,则????????2=(????+9) ????????.
?
练习
例2.(2)已知一个球内有相距9 ????????的两个平行截面,它们的面积分别为49???? ????????2和400???? ????????2,则球的表面积是_____????????2.
?
在?????????????1????????中,????2=????2+202,①
在?????????????2????????中,????2=72+(????+9)2,②
联立①②可得????=15,????=25.
∴????球=4????????2=2500????(????????2),
故球的表面积为2500???? ????????2 .
?
练习
例2.(2)已知一个球内有相距9 ????????的两个平行截面,它们的面积分别为49???? ????????2和400???? ????????2,则球的表面积是_____????????2.
?
解:当截面在球心的两侧时,如图②所示为球的轴截面,由球的截面性质知????1????//????2????,且????1,????2为两截面圆的圆心,则????????1⊥????1????,
????????2⊥????2????.设球的半径为????,
∵?????????2????2=49????,∴????2????=7 ????????.同理,得????1????=20 ????????.
设????????1=???? ????????,则????????2=(9?????) ????????.
在?????????????1????????中,????2=????2+400.在?????????????2????????中,????2=(9?????)2+49,
解得????=?15,不合题意,舍去.
综上所述,球的表面积为2500???? ????????2.
?
练习
方法技巧:
球的截面问题的解决方法
1.作经过球心和截面圆圆心的轴截面.
2.利用直角三角形求解,球的半径????,球心到截面的距离????,截面圆半径????恰好构成一个直角三角形,利用????2=????2?????2可知二求一.
?
练习
变2.平面????截球????的球面所得圆的半径为1,球的体积为43????,则球心????到平面????的距离为( ).
A.22 B.2 C.23 D.3
?
答案:B.
?
解:如图,设截面圆的圆心为????‘,????为截面圆上任一点.
由球的体积公式????=43????????3=43????,∴????=3.又????‘????=1,
所以????????‘=(3)2?1=2.即球心????到平面????的距离为2.故选B.
?
练习
题型三:与球有关的切、接问题
例3.(1)设三棱柱的侧棱垂直于底面,所有棱的长都为????,顶点都在一个球面上,则该球的表面积为( ).
A.????????2 B.73????????2 C.113????????2 D.5????????2
?
答案:B.
解:由题意知,该三棱柱为正三棱柱,且侧棱与底面边长相等,均为????.如图,????为三棱柱上底面的中心,????为球心,易知
????????=23×32????=33????,????????=12????,所以球的半径????=????????满足
????2=(33????)2+(12????)2=712????2,故????球=4????????2=73????????2.故选B.
?
练习
例3.(2)球的一个内接圆锥满足:球心到该圆锥底面的距离是球半径的一半,则该圆锥的体积和此球体积的比值为________.
答案:932或332.
?
解:①当圆锥顶点与底面在球心两侧时,如图所示,设球的半径为????,则球心到该圆锥底面的距离是????2,于是圆锥的底面半径为????2?(????2)2=32????,高为32????.该圆锥的体积为13×????×(32????)2×32????=38????????3,球体积为43????????3,所以该圆锥的体积和此球体积的比值为38????????343????????3=932.
②同理,当圆锥顶点与底面在球心同侧时,该圆锥的体积和此球体积的比值为332.
?
练习
方法技巧:
1.常见几何体与球的体与球的切、接问题的解决策略
(1)处理有关几何体外接球或内切球的相关问题时,要注意球心的位置与几何体的关系.一般情况下,由于球的对称性,球心总在特殊位置,比如中心、对角线的中点等.
(2)解决此类问题的实质就是根据几何体的相关数据求球的直径或半径,关键时根据“切点”和“接点”作出轴截面图,把空间问题转化为平面问题来计算.
练习
方法技巧:
2.几个常用结论
(1)球内切于正方体,切点为正方体各个面的中心,正方体的棱长等于球的直径.
(2)球外接于正方体,正方体的顶点均在球面上,正方体的体对角线等于球的直径.
(3)球与圆柱的底面和侧面均相切,则球的直径等于圆柱的高,也等于圆柱底面圆的直径.
练习
变3.若棱长为????的正四面体的各个顶点都在同一个球面上,则球的表面积为______.
?
答案:32????????2.
?
解:把正四面体放在正方体中,设正方体棱长为????,则????=2????,由题意知
2????=3????=3×2????2=6????2,所以????球=4????????2=32????????2.
?
课堂小结
1.圆柱、圆锥、圆台的表面积
????圆柱=????侧面+2????圆底
=2????????????+2????????2=2????????(????+????).
(????是底面半径,????是母线长)
?
????圆锥=????侧面+????圆底
=12×2????????×????+????????2=????????(????+????).
(????是底面半径,????是母线长)
?
课堂小结
1.圆柱、圆锥、圆台的表面积
????’
?
????圆台=????大锥?????小锥+????上底
=????????[(????+????‘)+????]?????????‘(????‘+????‘)+2????????‘2
=????????????+????????????‘+????????2?????????‘????‘+????????‘2
=????????????+????????2+????????‘2+????????‘(?????????‘)=????????????+????????????‘+????????2+????????‘2
=????(????‘2+????2+????????+????‘????).
(????‘,????分别是上、下底面半径,????是母线长)
?
课堂小结
2.圆柱、圆锥、圆台的体积
????圆柱=????????2?(????是底面半径,?是高),
????圆锥=13????????2?(????是底面半径,?是高),
????圆台=13?????(????‘2+????‘????+????2)(????‘,????分别是上、下底面半径,?是高).
?
课堂小结
1.球的表面积
设球的半径为????,则球的表面积是
????球=4????????2.
2.球的体积
设球的半径为????,则球的体积公式????球=43????????3.
的表面积与体积
l
O
O'
2πr
r
2πr
O
S
l
r
O'
O
r'
2πr'
r
l
2πr
我们知道了多面体的表面积,那你认为旋转体——圆柱、圆锥、圆台、球的表面积又是怎样的呢?
圆柱、圆锥、圆台的表面积是围成它们的各个面的面积和,即
复习引入
一、圆柱的表面积
l
O
O'
2πr
r
新知探索
2πr
O
S
l
r
二、圆锥的表面积
新知探索
O'
O
r'
2πr'
r
l
2πr
l'
三、圆台的表面积
l
新知探索
圆柱、圆锥、圆台的表面积公式之间有什么关系?你能用圆柱、圆锥、圆台的结构特征来解释这种关系吗?
r’=r
r’=0
上底扩大
上底缩小
S圆台=π(r’?+r?+r’l+rl)
S圆柱=2πr(r+l)
S圆锥=πr(r+l)
思考
新知探索
高h
柱体的体积 V=Sh
底面积S
棱柱和圆柱的体积
新知探索
A
B
C
D
E
O
S
底面积S
高h
棱锥和圆锥的体积
锥体的体积
新知探索
高h
棱台和圆台的体积
台体的体积
新知探索
l
O
O'
r
O
S
l
r
h
h
圆柱、圆锥、圆台体积
O'
O
r'
r
l
新知探索
圆柱、圆锥、圆台的体积公式之间有什么关系?你能用圆柱、圆锥、圆台的结构特征来解释这种关系吗?
r’=r
r’=0
上底扩大
上底缩小
思考
新知探索
新知探索
辨析1:判断正误.
1.圆锥的侧面展开图为扇形,其中扇形的弧长为圆锥底面圆的周长.( )
2.若圆柱的底面圆的直径与圆柱的高相等,则圆柱的侧面展开图是正方形. ( )
答案:√,×.
辨析2:若圆柱的底面半径为1,母线长为2,则它的侧面积为( ).
A.2???? B.3???? C.???? D.4????
?
答案:D.
割圆术
早在公元三世纪,我国数学家刘徽为推导圆的面积公式而发明了“倍边法割圆术”.他用加倍的方式不断增加圆内接正多边形的边数,使其面积与圆的面积之差更小,即所谓“割之弥细,所失弥小”.这样重复下去,就达到了“割之又割,以至于不可再割,则与圆合体而无所失矣”.这是世界上最早的“极限”思想.
新知探索
????球=????????????????
?
把一个半径为R的球的上半球横向切成n(无穷大)份, 每份等高并且把每份看成一个类似圆台,球的表面积为所有圆台的侧面积之和.
A
O
球体由n个这样的形状组成
球的表面积是大圆面积的4倍
新知探索
思考:在小学,我们学习了圆的面积公式,你还记得是如何求得的吗?类比这种方法,你能由球的表面积公式推导出球的体积公式吗?
如图,把球O的表面分成n个小网格,连接球心O和每个小网格的顶点,整个球体就被分割成n个“小锥体”.
O
A
B
C
D
O
A
B
C
D
当n越大,每个小网格越小时,每个“小锥体”的底面就越平,“小锥体”就越近似于棱锥,其高越近似于球半径R,设O-ABCD是其中一个“小锥体”,它的体积是
新知探索
思考:在小学,我们学习了圆的面积公式,你还记得是如何求得的吗?类比这种方法,你能由球的表面积公式推导出球的体积公式吗?
O
A
B
C
D
O
A
B
C
D
由于球的体积就是这n个“小锥体”的体积之和,而这n个“小锥体”的底面积之和就是球的表面积.因此,球的体积
由此,我们得到球的体积公式
新知探索
例1 如右图,某种浮标由两个半球和一个圆柱黏合而成,半球的直径是0.3m,圆柱高0.6m.如果在 浮标表面涂一层防水漆,每平方米需要0.5kg涂料,那么给1000个这样的浮标涂防水漆需要多少涂料?(π取3.14)
解:一个浮标的表面积为
2π×0.15×0.6 + 4π×0.152 =0.8478(m2)
所以给1000个这样的浮标涂防水漆约需涂料
0.8478×0.5×1000 =423.9(kg).
例析
例2 如右图,圆柱的底面直径和高都等于球的直径, 求球与圆柱的体积之比.
O
R
解:(1)设球的半径为R,则圆柱的底面半径为R,高为2R.
问题:球的表面积与圆柱的侧面积之比呢?
例析
练习
题型一:圆柱、圆锥、圆台的表面积
例1.(1)已知圆柱的上、下底面的中心分别为????1,????2,过直线????1????2的平面截该圆柱所得的截面是面积为8的正方形,则该圆柱的表面积为( ).
A.122???? B.12???? C.82???? D.10????
?
练习
题型一:圆柱、圆锥、圆台的表面积
例1.(1)已知圆柱的上、下底面的中心分别为????1,????2,过直线????1????2的平面截该圆柱所得的截面是面积为8的正方形,则该圆柱的表面积为( ).
A.122???? B.12???? C.82???? D.10????
?
答案:B.
解:因为过直线????1????2的平面截该圆柱所得的截面是面积为8的正方形,所以圆柱的高为22,底面圆的直径22为,所以该圆柱的表面积为2×????×(2)2+2????×2×22=12????.故选B.
?
练习
例1.(2)已知一个圆锥的轴截面是等边三角形,其面积为3,则这个圆锥的侧面积为_______.
?
答案:2????.
?
解:设母线长为????,由题意得12????????????????????? 60°=3,所以母线长????=2,又底面半径为1,所以侧面积为????×1×2=2????.
?
练习
方法技巧:
圆柱、圆锥、圆台的表面积的求解步骤:
1.得到空间几何体的平面展开图.
2.依次求出各个平面图形的面积.
3.将各平面图形的面积相加.
练习
例1.(2)已知一个圆锥的轴截面是等边三角形,其面积为3,则这个圆锥的侧面积为_______.
?
答案:2????.
?
解:设母线长为????,由题意得12????????????????????? 60°=3,所以母线长????=2,又底面半径为1,所以侧面积为????×1×2=2????.
?
练习
变1.(1)圆柱的一个底面积是????,侧面展开图是一个正方形,那么这个圆柱的侧面积是( ).
A.4???????? B.2???????? C.???????? D.233????????
?
练习
变1.(1)圆柱的一个底面积是????,侧面展开图是一个正方形,那么这个圆柱的侧面积是( ).
A.4???????? B.2???????? C.???????? D.233????????
?
答案:A.
?
解:底面半径是????????,所以正方形的边长是2π????????=2????????,故圆柱的侧面积是(2????????)2=4????????.故选A.
?
练习
变1.(2)轴截面是正三角形的圆锥称作等边圆锥,则等边圆锥的侧面积是底面积的( ).
A.4倍 B.3倍 C.2倍 D.2倍
?
变1.(3)已知圆台的上、下底面半径分别是2,6,且侧面面积等于两底面面积之和,则圆台的表面积是_______.
?
练习
变1.(2)轴截面是正三角形的圆锥称作等边圆锥,则等边圆锥的侧面积是底面积的( ).
A.4倍 B.3倍 C.2倍 D.2倍
?
答案:D.
?
解:由已知得????=2????,????侧????底=????????????????????2=????????=2,故选D.
?
变1.(3)已知圆台的上、下底面半径分别是2,6,且侧面面积等于两底面面积之和,则圆台的表面积是_______.
?
答案:80????.
?
解:设圆台母线长为????,则由题意得????(2+6)????=????×22+????×62,∴8????????=40????,∴????=5,∴????=????×(2+6)×5+????×22+????×62=40????+4????+36????=80????.
?
练习
题型二:圆柱、圆锥、圆台的体积
例2.(1)若一个圆柱与圆锥的高相等,且轴截面面积也相等,则圆柱与圆锥的体积之比是( ).
A.1 B.1:2 C.3:2 D.3:4
?
练习
题型二:圆柱、圆锥、圆台的体积
例2.(1)若一个圆柱与圆锥的高相等,且轴截面面积也相等,则圆柱与圆锥的体积之比是( ).
A.1 B.1:2 C.3:2 D.3:4
?
答案:D.
解:设圆柱、圆锥的高都为?,底面半径分别为????,????,则有12?2?????=2?????,所以????=2????,????圆锥=13????????2?=43????????2?,????圆柱=????????2?,故????圆锥:????圆锥=3:4.故选D.
?
练习
方法技巧:
求圆柱、圆锥、圆台的体积问题,一是要牢记公式,然后观察空间图形的构成,是单一的旋转体,还是组合体;二是注意旋转体的构成,以及圆柱、圆锥、圆台轴截面的性质,从而找出公式中需要的各个量,代入公式计算.
练习
例2.(2)设圆台的高为3,如图,在轴截面中母线????????1与底面直径????????的夹角为60°,轴截面中的一条对角线垂直于腰,则圆台的体积为_____.
?
解:设上、下底面半径,母线长分别为????,????,????.
作????1????⊥????????于点????,则????1????=3,∠????????1????=60°.
又∠????????1????=90°,∴∠????????1????=60°,∴????????=????1???????????????? 60°=3,∴?????????=3.
????????=????1?????????????????60°=33 ,∴????+????=33,∴????=23,????=3,而?=3.
∴????圆台=13?????(????2+????????+????2)=13????×3×[(23)2+23×3+(3)2]=21????.
∴圆台的体积为21????.
?
练习
变2.(1)若圆台上、下底面面积分别是????,4????,侧面积是4????,则这个圆台的体积是( ).
A.233???? B.23 C.736???? D.733????
?
答案:D.
?
解:????1=????,????2=4????,∴????=1,????=2,
????侧=6????=????(????+????)????,∴????=2,∴?=3.
∴????=13????(1+4+2)×3=733????.故选D.
?
练习
变2.(2)若圆锥的轴截面是等腰直角三角形,侧面积是162????,则圆锥的体积是( ).
A.643???? B.1283???? C.64???? D.1282????
?
答案:A.
?
解:设圆锥的底面半径为????,母线长为????.
∵圆锥的轴截面是等腰直角三角形,∴2????=????2+????2,即????=2????.
由题意得,侧面积????侧=?????????????=2????????2=162????,
∴????=4.∴????=42,高?=????2?????2=4.
∴圆锥的体积????=13?????=13????×42×4=643????.故选A.
?
练习
变2.(3)如图,一个底面半径为2的圆柱被一平面所截,截得的几何体的最短和最长母线长分别为2和3,则该几何体的体积为( ).
A.5???? B.6???? C.20???? D.10????
?
答案:D.
?
解:用一个完全相同的几何体把题中几何体补成一个圆柱,如图,则圆柱的体积为????×22×5=20????,故所求几何体的体积为10????.故选D.
?
练习
题型三:与组合体有关的表面积与体积问题
例3.(1)如图,在底面半径为2,母线长为4的圆锥中挖掉一个高为3的内接圆柱,求圆柱的表面积.
?
解:设圆锥的底面半径为????,圆柱的底面半径为????,表面积为????.
则????=????????=2,????????=4,????????=42?22=23.
如图所示,易知?????????????~?????????????,所以????????????????=????????????????,即323=????2,所以????=1,
????底=2????????2=2????,????侧=2??????????=23????.
所以????=????底+????侧=2????+23????=(2+23)????.
所以圆柱的表面积为(2+23)????.
?
练习
例3.(2)如图,在底面半径为2,母线长为4的圆锥中挖掉一个高为3的内接圆柱,求圆柱的体积与圆锥的体积之比.
?
解:由(1)知,圆柱的底面半径为????=1,高?=3,
所以圆柱的体积????1=????????2?=????×12×3=3????.
圆锥的体积????2=13????×22×23=833????.
所以圆柱与圆锥的体积比为3:8.
?
练习
例3.(3)如图,在底面半径为2,母线长为4的圆锥中挖掉一个高为?的内接圆柱,试求圆柱侧面积的最大值.
?
解:设圆锥的底面半径为????,圆柱的底面半径为????,
则????=????????=2,????????=4,????????=42?22=23.
易知?????????????~?????????????,所以????????????????=????????????????,即23??23=????2,
所以?=23?3????,????圆柱侧=2?????????=2????????(23?3????)=?23????????2+43????????,
所以当????=1,?=3时,圆柱的侧面积最大,其最大值为23????.
?
练习
方法技巧:
关于组合体的表面积与体积问题的解题策略
(1)分析结构特征:弄清组合体的组成形式,找准有关简单几何体的关键量.
(2)设计计算方法:根据组成形式,设计计算方法,特别要注意“拼接面”面积的处理,利用“切割”“补形”的方法求体积.
(3)计算求值:根据设计的计算方法求值.
[提醒]组合体分割成规则的几何体求表面积、体积之和(或差),保证不重不漏.
练习
变3.如图所示,一圆柱内挖去一个圆锥,圆锥的顶点是圆柱底面的圆心,圆锥的底面是圆柱的另一个底面.圆柱的母线长为6,底面半径为2.求该组合体的表面积.
?
解:挖去的圆锥的母线长为62+22=210,则圆锥的侧面积等于410????.圆柱的侧面积为2????×2×6=24????,圆柱的一个底面面积为????×22=4????,所以组合体的表面积为410????+24????+4????=(410+28)????.
?
练习
题型一:球的表面积和体积
例1.(1)一个球的表面积是16????,则它的体积是( ).
A.64???? B.643???? C.32???? D.323????
?
答案:D.
解:设球的半径为????,则由题意可知4????????2=16????,故????=2.
所以球的体积????=43????????3=323????.故选D.
?
练习
例1.(2)已知球的体积为5003????,则它的表面积为_____.
?
答案:100????.
?
解:设球的半径为????,由已知得43????????3=5003????,故????=5.
所以球的表面积????=4????????2=4????×52=100????.
?
练习
方法技巧:
1.球的体积与表面积的求法:必须知道半径????或者通过条件能求出半径????,然后代入体积或表面积公式求解.
2.关键要素:半径和球心是球的关键要素,把握住了这两点,计算球的表面积或体积的相关题目也就轻松自如了.
?
练习
变1.(1)若一个球的表面积与其体积在数值上相等,则此球的半径为______.
答案:3.
?
解:设此球的半径为R,则4????????2=43????????3,解得????=3.
?
变2.(2)如果三个球的半径之比是1:2:3,那么最大球的表面积是其余两个球的表面积之和的______倍.
?
答案:95.
?
解:设小球半径为1,则大球的表面积????大=36????,????小+????中=20????,36????20????=95.
?
练习
题型二:球的截面问题
例2.(1)一平面截一球得到直径为25 ????????的圆面,球心到这个平面的距离是2 ????????,则该球的体积是( ).
A.12???? ????????3 B.36???? ????????3 C.646???? ????????3 D.108???? ????????3
?
答案:B.
解:设球心为????,截面圆心为????1,连接????????1,则????????1垂直于截面圆????1,如图所示.在?????????????????1????中,????1????=5 ????????,????????1=2 ????????,
∴球的半径????=????????=22+(5)2=3(????????),
∴球的体积????=43????×33=36????(????????3).故选B.
?
练习
例2.(2)已知一个球内有相距9 ????????的两个平行截面,它们的面积分别为49???? ????????2和400???? ????????2,则球的表面积是_____????????2.
?
答案:2500????.
?
解:当截面在球心的同侧时,如图①所示为球的轴截面,由球的截面性质知????????1//????????2,且????1,????2为两截面圆的圆心,则????????1⊥????????1,
????????2⊥????????2.设球的半径为????,
∵?????????2????2=49????,∴????2????=7 ????????.
同理,得????1????=20 ????????.
设????????1=???? ????????,则????????2=(????+9) ????????.
?
练习
例2.(2)已知一个球内有相距9 ????????的两个平行截面,它们的面积分别为49???? ????????2和400???? ????????2,则球的表面积是_____????????2.
?
在?????????????1????????中,????2=????2+202,①
在?????????????2????????中,????2=72+(????+9)2,②
联立①②可得????=15,????=25.
∴????球=4????????2=2500????(????????2),
故球的表面积为2500???? ????????2 .
?
练习
例2.(2)已知一个球内有相距9 ????????的两个平行截面,它们的面积分别为49???? ????????2和400???? ????????2,则球的表面积是_____????????2.
?
解:当截面在球心的两侧时,如图②所示为球的轴截面,由球的截面性质知????1????//????2????,且????1,????2为两截面圆的圆心,则????????1⊥????1????,
????????2⊥????2????.设球的半径为????,
∵?????????2????2=49????,∴????2????=7 ????????.同理,得????1????=20 ????????.
设????????1=???? ????????,则????????2=(9?????) ????????.
在?????????????1????????中,????2=????2+400.在?????????????2????????中,????2=(9?????)2+49,
解得????=?15,不合题意,舍去.
综上所述,球的表面积为2500???? ????????2.
?
练习
方法技巧:
球的截面问题的解决方法
1.作经过球心和截面圆圆心的轴截面.
2.利用直角三角形求解,球的半径????,球心到截面的距离????,截面圆半径????恰好构成一个直角三角形,利用????2=????2?????2可知二求一.
?
练习
变2.平面????截球????的球面所得圆的半径为1,球的体积为43????,则球心????到平面????的距离为( ).
A.22 B.2 C.23 D.3
?
答案:B.
?
解:如图,设截面圆的圆心为????‘,????为截面圆上任一点.
由球的体积公式????=43????????3=43????,∴????=3.又????‘????=1,
所以????????‘=(3)2?1=2.即球心????到平面????的距离为2.故选B.
?
练习
题型三:与球有关的切、接问题
例3.(1)设三棱柱的侧棱垂直于底面,所有棱的长都为????,顶点都在一个球面上,则该球的表面积为( ).
A.????????2 B.73????????2 C.113????????2 D.5????????2
?
答案:B.
解:由题意知,该三棱柱为正三棱柱,且侧棱与底面边长相等,均为????.如图,????为三棱柱上底面的中心,????为球心,易知
????????=23×32????=33????,????????=12????,所以球的半径????=????????满足
????2=(33????)2+(12????)2=712????2,故????球=4????????2=73????????2.故选B.
?
练习
例3.(2)球的一个内接圆锥满足:球心到该圆锥底面的距离是球半径的一半,则该圆锥的体积和此球体积的比值为________.
答案:932或332.
?
解:①当圆锥顶点与底面在球心两侧时,如图所示,设球的半径为????,则球心到该圆锥底面的距离是????2,于是圆锥的底面半径为????2?(????2)2=32????,高为32????.该圆锥的体积为13×????×(32????)2×32????=38????????3,球体积为43????????3,所以该圆锥的体积和此球体积的比值为38????????343????????3=932.
②同理,当圆锥顶点与底面在球心同侧时,该圆锥的体积和此球体积的比值为332.
?
练习
方法技巧:
1.常见几何体与球的体与球的切、接问题的解决策略
(1)处理有关几何体外接球或内切球的相关问题时,要注意球心的位置与几何体的关系.一般情况下,由于球的对称性,球心总在特殊位置,比如中心、对角线的中点等.
(2)解决此类问题的实质就是根据几何体的相关数据求球的直径或半径,关键时根据“切点”和“接点”作出轴截面图,把空间问题转化为平面问题来计算.
练习
方法技巧:
2.几个常用结论
(1)球内切于正方体,切点为正方体各个面的中心,正方体的棱长等于球的直径.
(2)球外接于正方体,正方体的顶点均在球面上,正方体的体对角线等于球的直径.
(3)球与圆柱的底面和侧面均相切,则球的直径等于圆柱的高,也等于圆柱底面圆的直径.
练习
变3.若棱长为????的正四面体的各个顶点都在同一个球面上,则球的表面积为______.
?
答案:32????????2.
?
解:把正四面体放在正方体中,设正方体棱长为????,则????=2????,由题意知
2????=3????=3×2????2=6????2,所以????球=4????????2=32????????2.
?
课堂小结
1.圆柱、圆锥、圆台的表面积
????圆柱=????侧面+2????圆底
=2????????????+2????????2=2????????(????+????).
(????是底面半径,????是母线长)
?
????圆锥=????侧面+????圆底
=12×2????????×????+????????2=????????(????+????).
(????是底面半径,????是母线长)
?
课堂小结
1.圆柱、圆锥、圆台的表面积
????’
?
????圆台=????大锥?????小锥+????上底
=????????[(????+????‘)+????]?????????‘(????‘+????‘)+2????????‘2
=????????????+????????????‘+????????2?????????‘????‘+????????‘2
=????????????+????????2+????????‘2+????????‘(?????????‘)=????????????+????????????‘+????????2+????????‘2
=????(????‘2+????2+????????+????‘????).
(????‘,????分别是上、下底面半径,????是母线长)
?
课堂小结
2.圆柱、圆锥、圆台的体积
????圆柱=????????2?(????是底面半径,?是高),
????圆锥=13????????2?(????是底面半径,?是高),
????圆台=13?????(????‘2+????‘????+????2)(????‘,????分别是上、下底面半径,?是高).
?
课堂小结
1.球的表面积
设球的半径为????,则球的表面积是
????球=4????????2.
2.球的体积
设球的半径为????,则球的体积公式????球=43????????3.
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
