平面向量的基本定理及坐标表示(广东省惠州市惠城区)
文档属性
| 名称 | 平面向量的基本定理及坐标表示(广东省惠州市惠城区) |  | |
| 格式 | rar | ||
| 文件大小 | 267.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-09-09 13:21:00 | ||
图片预览

文档简介
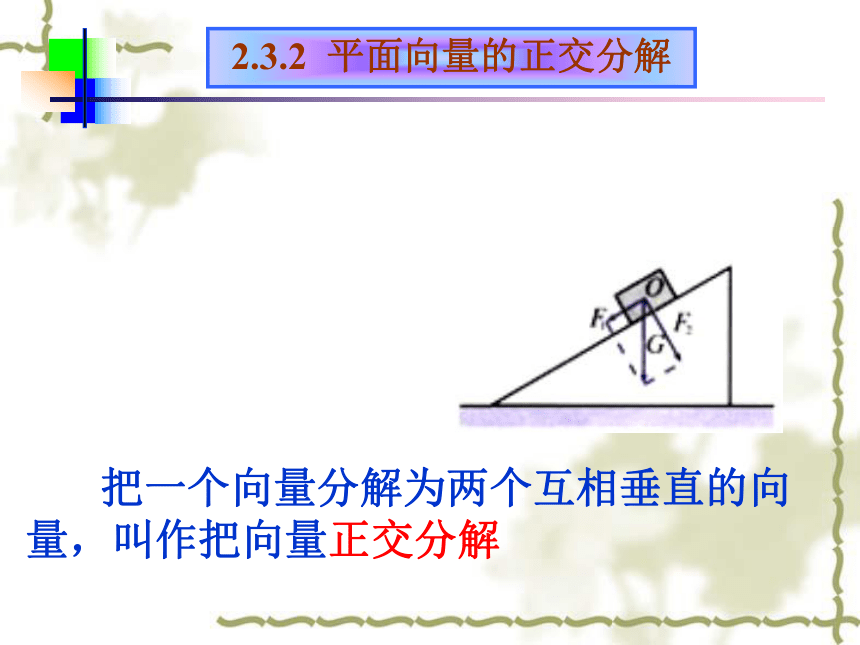
课件10张PPT。2.3.2 平面向量的正交分解
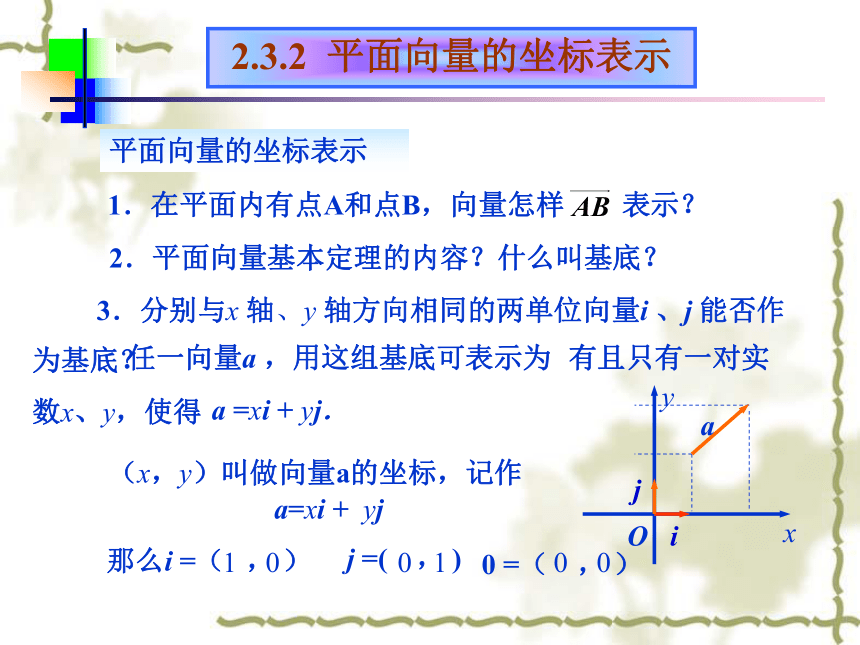
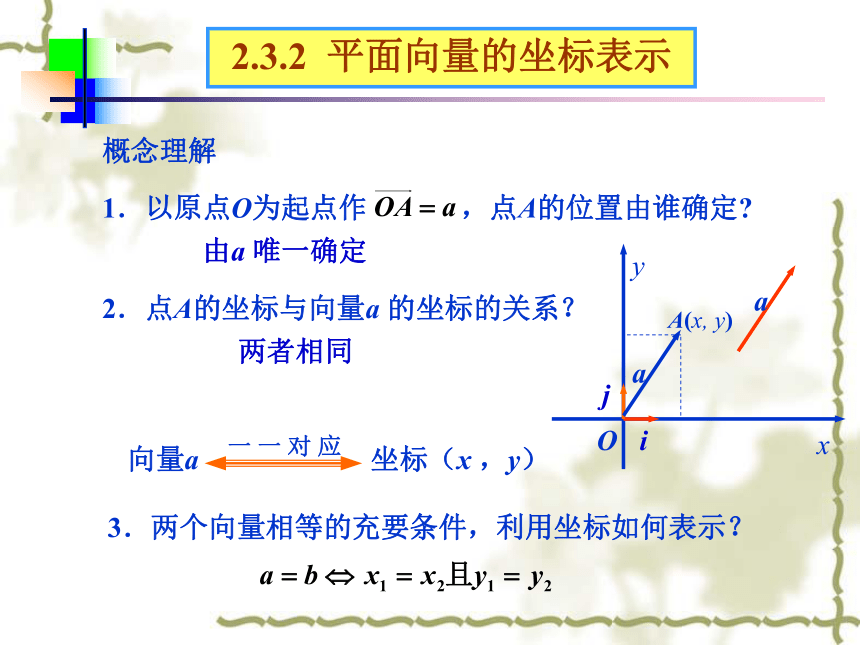
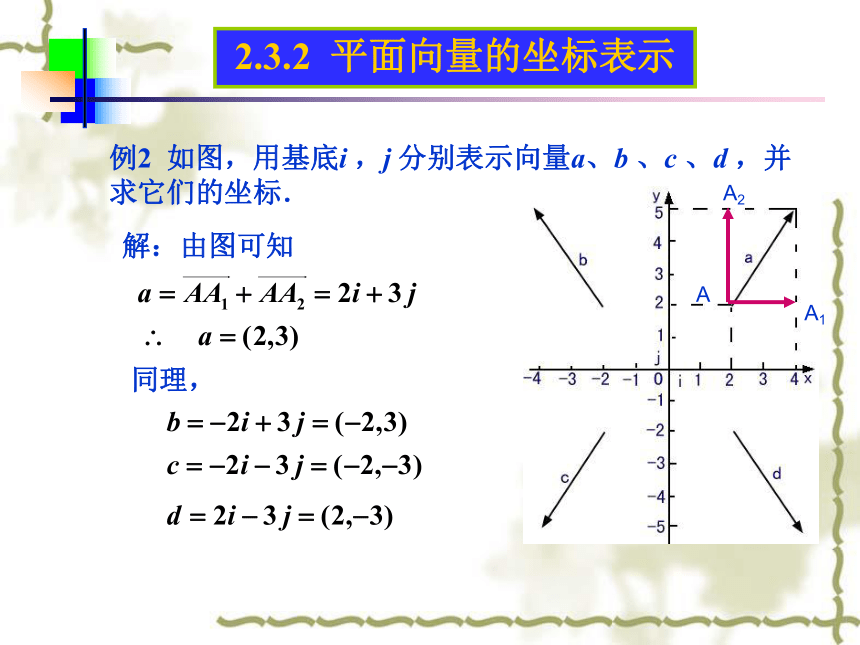
及坐标表示2.3.3 平面向量的坐标运算 把一个向量分解为两个互相垂直的向量,叫作把向量正交分解2.3.2 平面向量的正交分解2.3.2 平面向量的坐标表示平面向量的坐标表示1.在平面内有点A和点B,向量怎样 表示?2.平面向量基本定理的内容?什么叫基底? 1 00 10 02.3.2 平面向量的坐标表示由a 唯一确定2.点A的坐标与向量a 的坐标的关系?两者相同概念理解3.两个向量相等的充要条件,利用坐标如何表示?2.3.2 平面向量的坐标表示解:由图可知同理,2.3.3平面向量的坐标运算平面向量的坐标运算1.已知a , b ,求a+b,a-b.解:a+b=( i + j ) + ( i + j )=( + )i+( + )j两个向量和(差)的坐标分别等于这两个向量相应
坐标的和(差)2.3.3平面向量的坐标运算解: 一个向量的坐标等于表示此向量的有向线段的终点的坐
标减去始点的坐标. 实数与向量的积的坐标等于这个实数乘原来的向量的相
应坐标.2.3.3 平面向量的坐标运算 例4 已知a=(2,1),b=(-3,4),求a+b,
a-b,3a+4b的坐标.a-b=(2,1)-(-3,4)=(5,-3);3a+4b=3(2,1)+4(-3,4)
=(6,3)+(-12,16)
=(-6,19)2.3.3 平面向量的坐标运算 例5 已知 ABCD的三个顶点A、B、C的坐标分别为
(-2,1)、( -1,3)、(3,4),求顶点D的坐标.解法1:设顶点D的坐标为(x,y)例5 已知 ABCD的三个顶点A、B、C的坐标分别为
(-2,1)、( -1,3)、(3,4),求顶点D的坐标.解法2:由平行四边形法则可得而所以顶点D的坐标为(2,2)
及坐标表示2.3.3 平面向量的坐标运算 把一个向量分解为两个互相垂直的向量,叫作把向量正交分解2.3.2 平面向量的正交分解2.3.2 平面向量的坐标表示平面向量的坐标表示1.在平面内有点A和点B,向量怎样 表示?2.平面向量基本定理的内容?什么叫基底? 1 00 10 02.3.2 平面向量的坐标表示由a 唯一确定2.点A的坐标与向量a 的坐标的关系?两者相同概念理解3.两个向量相等的充要条件,利用坐标如何表示?2.3.2 平面向量的坐标表示解:由图可知同理,2.3.3平面向量的坐标运算平面向量的坐标运算1.已知a , b ,求a+b,a-b.解:a+b=( i + j ) + ( i + j )=( + )i+( + )j两个向量和(差)的坐标分别等于这两个向量相应
坐标的和(差)2.3.3平面向量的坐标运算解: 一个向量的坐标等于表示此向量的有向线段的终点的坐
标减去始点的坐标. 实数与向量的积的坐标等于这个实数乘原来的向量的相
应坐标.2.3.3 平面向量的坐标运算 例4 已知a=(2,1),b=(-3,4),求a+b,
a-b,3a+4b的坐标.a-b=(2,1)-(-3,4)=(5,-3);3a+4b=3(2,1)+4(-3,4)
=(6,3)+(-12,16)
=(-6,19)2.3.3 平面向量的坐标运算 例5 已知 ABCD的三个顶点A、B、C的坐标分别为
(-2,1)、( -1,3)、(3,4),求顶点D的坐标.解法1:设顶点D的坐标为(x,y)例5 已知 ABCD的三个顶点A、B、C的坐标分别为
(-2,1)、( -1,3)、(3,4),求顶点D的坐标.解法2:由平行四边形法则可得而所以顶点D的坐标为(2,2)
