7.1.2平面直角坐标系课后练习(含答案)2022-2023学年人教版七年级数学下册
文档属性
| 名称 | 7.1.2平面直角坐标系课后练习(含答案)2022-2023学年人教版七年级数学下册 |

|
|
| 格式 | zip | ||
| 文件大小 | 244.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-16 09:53:07 | ||
图片预览


文档简介
7.1.2平面直角坐标系 课后练习
一、单选题
1.点()在第二、四象限的角平分线上,则m的值为( )
A. B.5 C.-5 D.
2.在平面直角坐标系中,位于第二象限的点是( )
A.(-2,-3) B.(2,4) C.(-2,3) D.(2,-3)
3.平面直角坐标系内有一点A(a,b),若ab=0,则点A的位置在( )
A.原点 B.x轴上 C.y轴上 D.坐标轴上
4.在平面直角坐标系中,点P的坐标为,则点P所在的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
5.已知轴上的点到轴的距离为3,则点的坐标是( )
A. B. C.或 D.或
6.下列命题不正确的是( )
A.平行于x轴的直线上的所有点的纵坐标都相同
B.在平面直角坐标系中,和表示两个不同的点
C.若点在y轴上,则
D.到x轴的距离为3
7.如图是坐标系的一部分,若M位于点(2,2)上,N位于点(4,2)上,则G位于点( )上.
A.(1,3) B.(1,1) C.(0,1) D.(1,1)
8.点A、B是平面直角坐标系中轴上的两点,且,有一点与构成三角形,若的面积为3,则点的纵坐标为( )
A.3 B.3或 C.2 D.2或
9.在平面直角坐标系中,点的坐标是.若点到轴的距离与到轴的距离相等,则的值为( )
A. B. C.1或3 D.2或3
10.如图,在平面直角坐标系中,设一质点M自 处向上运动1个单位至 ,然后向左运动2个单位至 处,再向下运动3个单位至处,再向右运动4个单位至处,再向上运动5个单位至处,……,如此继续运动下去,则的坐标为( )
A. B.
C. D.
二、填空题
11.点M(﹣3,4)到y轴的距离是__.
12.已知同号,则点P(,)在第___________象限;
13.在平面直角坐标系中,第四象限内有一点,点到轴的距离为,到轴的距离为,则点的坐标是_____.
14.如图,在平面直角坐标系中,一动点从原点O出发,每次移动1个单位长度,依次得到点P1(0,1),P2(1,1),P3(1,0),P4(1,﹣1),P5(2,﹣1),P6(2,0) ,则P2020的坐标是___.
15.点P(2a,1-3a)是第二象限内的一个点,且点P到两坐标轴的距离之和为6,则点P的坐标是________.
三、解答题
16.若点在第一、三象限的角平分线上,求a的值.
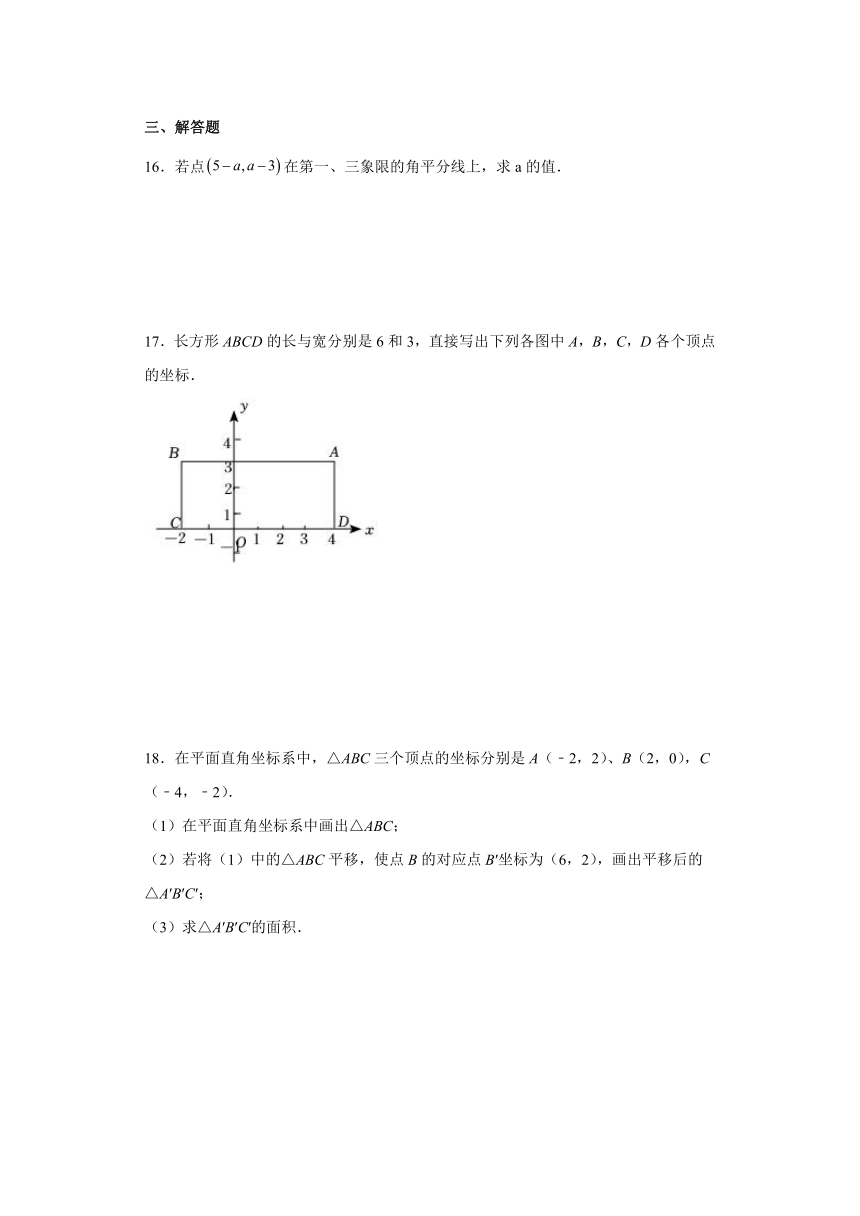
17.长方形ABCD的长与宽分别是6和3,直接写出下列各图中A,B,C,D各个顶点的坐标.
18.在平面直角坐标系中,△ABC三个顶点的坐标分别是A(﹣2,2)、B(2,0),C(﹣4,﹣2).
(1)在平面直角坐标系中画出△ABC;
(2)若将(1)中的△ABC平移,使点B的对应点B′坐标为(6,2),画出平移后的△A′B′C′;
(3)求△A′B′C′的面积.
19.在平面直角坐标系中,△ABC的顶点坐标分别为A(2,0),B(0,4),C(﹣3,2),P的坐标为(m,0).
(1)直接写出线段AP的长为 (用含m的式子表示);
(2)求△ABC的面积;
(3)当S△PAB=2S△ABC时,求m的值.
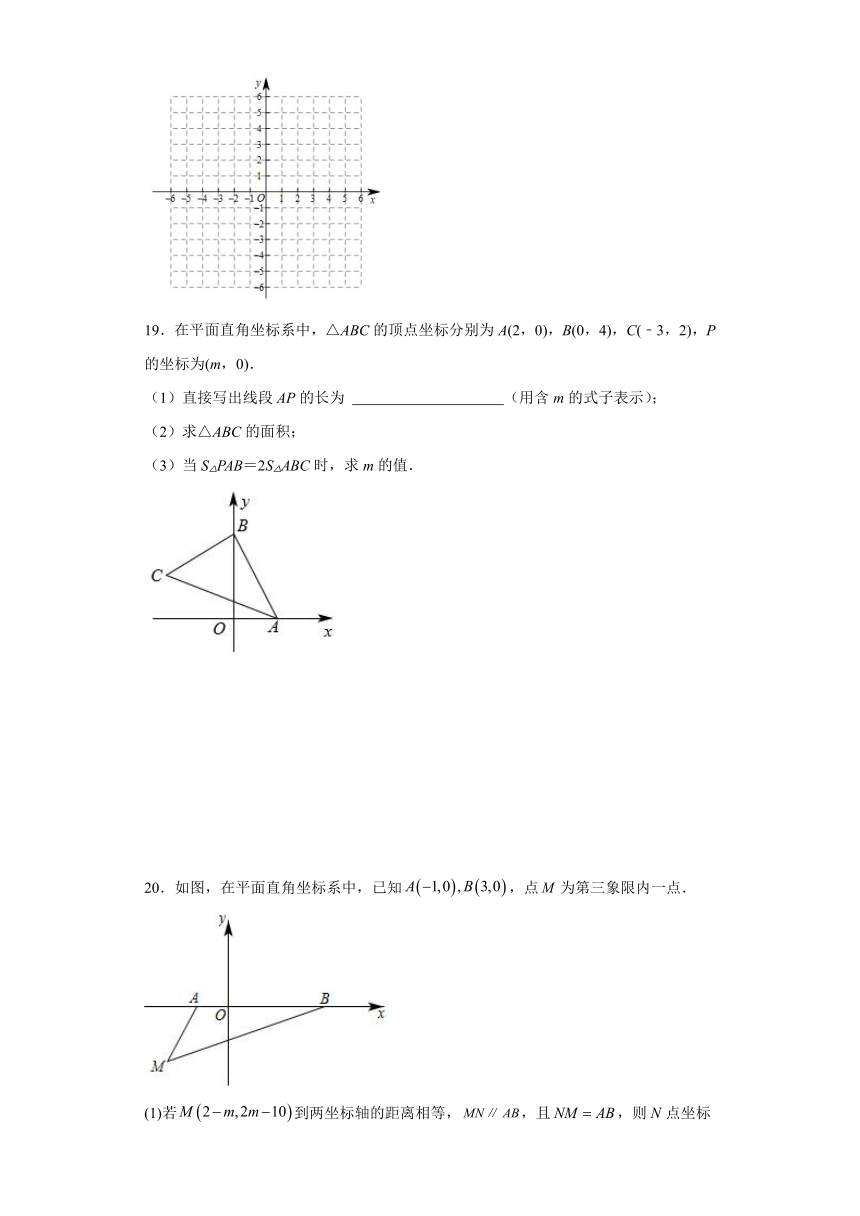
20.如图,在平面直角坐标系中,已知,点为第三象限内一点.
(1)若到两坐标轴的距离相等,,且,则点坐标为______.
(2)若为,请用含的式子表示的面积.
(3)在(2)条件下,当时,在轴上有点,使得的面积是的面积的2倍,请直接写出点的坐标.
参考答案
1.D
2.C
3.D
4.B
5.D
6.D
7.C
8.B
9.C
10.B
11.3
12.一或三
13.
14.(673,-1)
15.(-2,4)
16.解:∵点(5-a,a-3)在第一、三象限角平分线上,且第一、三象限角平分线上的点的坐标特点为:点的横纵坐标相等,
∴5-a=a-3,即a=4.
17.∵长方形ABCD的长与宽分别是6和3,
∴CD=6,AD=BC=3,
又由图可得,C在x轴负半轴上,D在x轴正半轴上,点A在第一象限,点B在第二象限,
∴,,,.
18.解:(1)如图,△ABC为所作;
(2)如图,△A′B′C′为所作;
(3)△A′B′C′的面积=.
19.解:(1)A(2,0), P的坐标为(m,0).
AP=,
故答案为:.
(2)如图,作CD⊥x轴,过B作BE⊥DC的延长线于E,作AF⊥EB交EB的延长线于F,可得四边形ADEF为矩形.
∴D(﹣3,0),E(﹣3,4),F(2,4),
∴S△ABC=S矩形ADEF﹣S△BEC﹣S△CDA﹣S△ABF
=5×4﹣﹣﹣
=20﹣3﹣5﹣4
=8.
故△ABC的面积为8.
(3)当S△PAB=2S△ABC时,
S△PAB=2×8=16,
即=16,
即×4=32,
解得:m=10或﹣6.
20(1)解:∵到坐标轴的距离相等,
∴,或8,
∵M为第三象限内一点,
∴,
∴,
∵,且,
∵,且,
∴或.
故答案为:或;
(2)∵M为,且M在第三象限,
∴,
∴的面积;
(3)当时,的面积为,
∵的面积是的面积的2倍,
∴,
∴,,
∴或.
一、单选题
1.点()在第二、四象限的角平分线上,则m的值为( )
A. B.5 C.-5 D.
2.在平面直角坐标系中,位于第二象限的点是( )
A.(-2,-3) B.(2,4) C.(-2,3) D.(2,-3)
3.平面直角坐标系内有一点A(a,b),若ab=0,则点A的位置在( )
A.原点 B.x轴上 C.y轴上 D.坐标轴上
4.在平面直角坐标系中,点P的坐标为,则点P所在的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
5.已知轴上的点到轴的距离为3,则点的坐标是( )
A. B. C.或 D.或
6.下列命题不正确的是( )
A.平行于x轴的直线上的所有点的纵坐标都相同
B.在平面直角坐标系中,和表示两个不同的点
C.若点在y轴上,则
D.到x轴的距离为3
7.如图是坐标系的一部分,若M位于点(2,2)上,N位于点(4,2)上,则G位于点( )上.
A.(1,3) B.(1,1) C.(0,1) D.(1,1)
8.点A、B是平面直角坐标系中轴上的两点,且,有一点与构成三角形,若的面积为3,则点的纵坐标为( )
A.3 B.3或 C.2 D.2或
9.在平面直角坐标系中,点的坐标是.若点到轴的距离与到轴的距离相等,则的值为( )
A. B. C.1或3 D.2或3
10.如图,在平面直角坐标系中,设一质点M自 处向上运动1个单位至 ,然后向左运动2个单位至 处,再向下运动3个单位至处,再向右运动4个单位至处,再向上运动5个单位至处,……,如此继续运动下去,则的坐标为( )
A. B.
C. D.
二、填空题
11.点M(﹣3,4)到y轴的距离是__.
12.已知同号,则点P(,)在第___________象限;
13.在平面直角坐标系中,第四象限内有一点,点到轴的距离为,到轴的距离为,则点的坐标是_____.
14.如图,在平面直角坐标系中,一动点从原点O出发,每次移动1个单位长度,依次得到点P1(0,1),P2(1,1),P3(1,0),P4(1,﹣1),P5(2,﹣1),P6(2,0) ,则P2020的坐标是___.
15.点P(2a,1-3a)是第二象限内的一个点,且点P到两坐标轴的距离之和为6,则点P的坐标是________.
三、解答题
16.若点在第一、三象限的角平分线上,求a的值.
17.长方形ABCD的长与宽分别是6和3,直接写出下列各图中A,B,C,D各个顶点的坐标.
18.在平面直角坐标系中,△ABC三个顶点的坐标分别是A(﹣2,2)、B(2,0),C(﹣4,﹣2).
(1)在平面直角坐标系中画出△ABC;
(2)若将(1)中的△ABC平移,使点B的对应点B′坐标为(6,2),画出平移后的△A′B′C′;
(3)求△A′B′C′的面积.
19.在平面直角坐标系中,△ABC的顶点坐标分别为A(2,0),B(0,4),C(﹣3,2),P的坐标为(m,0).
(1)直接写出线段AP的长为 (用含m的式子表示);
(2)求△ABC的面积;
(3)当S△PAB=2S△ABC时,求m的值.
20.如图,在平面直角坐标系中,已知,点为第三象限内一点.
(1)若到两坐标轴的距离相等,,且,则点坐标为______.
(2)若为,请用含的式子表示的面积.
(3)在(2)条件下,当时,在轴上有点,使得的面积是的面积的2倍,请直接写出点的坐标.
参考答案
1.D
2.C
3.D
4.B
5.D
6.D
7.C
8.B
9.C
10.B
11.3
12.一或三
13.
14.(673,-1)
15.(-2,4)
16.解:∵点(5-a,a-3)在第一、三象限角平分线上,且第一、三象限角平分线上的点的坐标特点为:点的横纵坐标相等,
∴5-a=a-3,即a=4.
17.∵长方形ABCD的长与宽分别是6和3,
∴CD=6,AD=BC=3,
又由图可得,C在x轴负半轴上,D在x轴正半轴上,点A在第一象限,点B在第二象限,
∴,,,.
18.解:(1)如图,△ABC为所作;
(2)如图,△A′B′C′为所作;
(3)△A′B′C′的面积=.
19.解:(1)A(2,0), P的坐标为(m,0).
AP=,
故答案为:.
(2)如图,作CD⊥x轴,过B作BE⊥DC的延长线于E,作AF⊥EB交EB的延长线于F,可得四边形ADEF为矩形.
∴D(﹣3,0),E(﹣3,4),F(2,4),
∴S△ABC=S矩形ADEF﹣S△BEC﹣S△CDA﹣S△ABF
=5×4﹣﹣﹣
=20﹣3﹣5﹣4
=8.
故△ABC的面积为8.
(3)当S△PAB=2S△ABC时,
S△PAB=2×8=16,
即=16,
即×4=32,
解得:m=10或﹣6.
20(1)解:∵到坐标轴的距离相等,
∴,或8,
∵M为第三象限内一点,
∴,
∴,
∵,且,
∵,且,
∴或.
故答案为:或;
(2)∵M为,且M在第三象限,
∴,
∴的面积;
(3)当时,的面积为,
∵的面积是的面积的2倍,
∴,
∴,,
∴或.
