浙教版七年级上册第六章 图形的初步知识 单元测试卷 无答案
文档属性
| 名称 | 浙教版七年级上册第六章 图形的初步知识 单元测试卷 无答案 |  | |
| 格式 | docx | ||
| 文件大小 | 333.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-16 11:15:26 | ||
图片预览


文档简介
第6章《图形的初步知识》
一、选择题
1.(本题3分)(2022·浙江金华·七年级期末)下列图形中,线段能表示点P到直线l的距离的是( ).
A.B.C.D.
2.(本题3分)(2022·浙江舟山·七年级期末)下列四个图中,能用∠1、∠AOB、∠O三种方法表示同一个角的是( )
A.B.C.D.
3.(本题3分)(2020·浙江·七年级期末)点C在线段上,下列条件中不能确定点C是线段中点的是( )
A. B. C. D.
4.(本题3分)(2020·浙江·台州市路桥实验中学七年级阶段练习)如图,已知直线AB,CD相交于点O,OE平分∠COB,如果∠EOB=55°,那么∠BOD的度数是( )
A.35° B.55° C.70° D.110°
5.(本题3分)(2020·浙江宁波·七年级期末)一个角的余角比它的补角的一半少,则这个角的度数为( )
A. B. C. D.
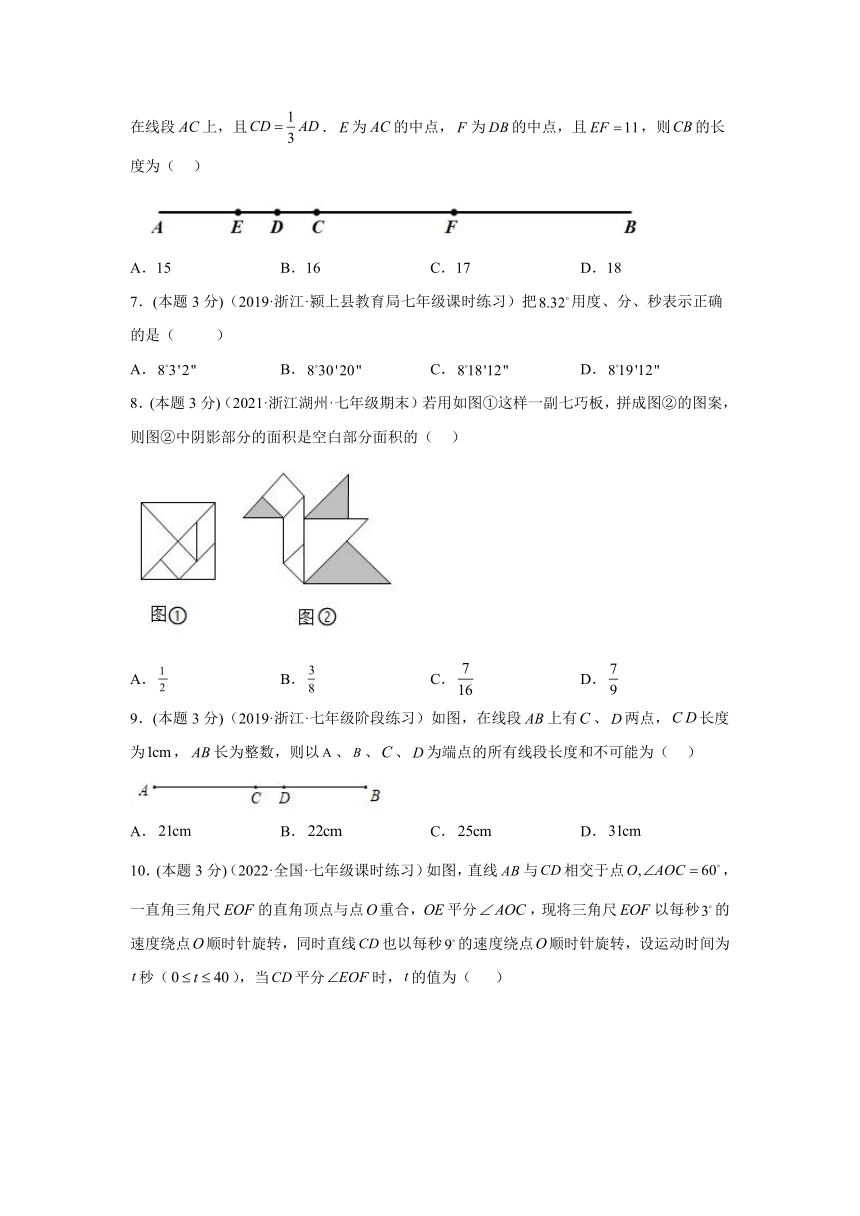
6.(本题3分)(2020·浙江宁波·七年级期末)如图,点在线段上,且.点在线段上,且.为的中点,为的中点,且,则的长度为( )
A.15 B.16 C.17 D.18
7.(本题3分)(2019·浙江·颍上县教育局七年级课时练习)把用度、分、秒表示正确的是( )
A. B. C. D.
8.(本题3分)(2021·浙江湖州·七年级期末)若用如图①这样一副七巧板,拼成图②的图案,则图②中阴影部分的面积是空白部分面积的( )
A. B. C. D.
9.(本题3分)(2019·浙江·七年级阶段练习)如图,在线段上有、两点,长度为,长为整数,则以、、、为端点的所有线段长度和不可能为( )
A. B. C. D.
10.(本题3分)(2022·全国·七年级课时练习)如图,直线与相交于点,一直角三角尺的直角顶点与点重合,平分,现将三角尺以每秒的速度绕点顺时针旋转,同时直线也以每秒的速度绕点顺时针旋转,设运动时间为秒(),当平分时,的值为( )
A. B. C.或 D.或
二、填空题
11.(2021·湖北·公安县教学研究中心七年级期末)若的度数为,且与互余,则的度数为____.
12.(2021·吉林省第二实验高新学校七年级阶段练习)如图,经过刨平的木板上的两个点,能弹出一条笔直的墨线,而且只能弹出一条墨线,能解释这一实际应用的数学知识是 _____.
13.(2022·山东·日照市北京路中学七年级期中)如图,AB、CD相交于点O,OM平分∠BOD,∠MON是直角,,则∠DON的度数是__________.
14.(2022·浙江·宁波市海曙外国语学校七年级开学考试)点O为直线l上一点,射线OA、OB均与直线l重合,将射线OB绕点O逆时针旋转α(0≤α≤90°),过点O作射线OC、OD、OM、ON,使得∠BOC=90°,∠COD=2α,∠COM=∠AOC,∠CON=∠COD(OM在∠AOC内部,ON在∠COD内部),当∠MON=α时,则α=_____.
15.(2020·浙江杭州·模拟预测)如图,点是线段上一点,,若的长为,则的长为______.
16.(2020·浙江绍兴·七年级阶段练习)如图,点A、O、B都在直线MN上,射线OA绕点O按顺时针方向以每秒4°的速度旋转,同时射线OB绕点O按逆时针方向以每秒6°的速度旋转(当其中一条射线与直线MN叠合时,两条射线停止旋转).经过____________秒,∠AOB的大小恰好是60°.
三、解答题
17.(2020·浙江省义乌市稠江中学七年级阶段练习)如图:A,B,C是平面上三个点,按下列要求画出图形.
(1)作直线BC,射线AB,线段AC.
(2)小明认为从A到C的所有线中,线段AC最短,其数学依据是 .
18.(2022·浙江金华·七年级期末)如图,已知OB是内一条射线,OE平分,OF平分.
(1)若,,求的度数;
(2)试判断是否成立.并请说明理由.
19.(2021·浙江省衢州市衢江区实验中学七年级开学考试)如图,线段AC=10cm,点M是AC的中点,在CB上取一点N,使得CN︰NB=3︰4,若CN=,求MN的长.
20.(2022·浙江台州·七年级阶段练习)如图,直线CD,EF相交于点O,射线OA在∠COF的内部,∠DOF=∠AOD.
(1)如图1,若∠AOC=120°,求∠EOC的度数;
(2)如图2,若∠AOC=α(60°<α<180°),将射线OA绕点O逆时针旋转60°,到OB,
①求∠EOB的度数(用含α的式子表示);
②观察①中的结果,直接写出∠AOC,∠EOB之间的数量关系.
如图3 ,0°<∠AOC <120°,将射线OA绕点O顺时针旋转60°,到OB,请直接写出∠AOC,∠EOB之间的数量关系.
21.(2022·浙江宁波·七年级期末)如图(1).点在线段上.图中共有三条线段: 线段, 线段, 线段, 若其中有一条线段的长度是另一条线段长度的两掊, 则称点为线段的 “奇分点”.若, 如图(2), 点从点开始以每秒3cm的速度向A运动,当点M到达A点时停止运动,运动的时间为t秒.当t=_____________秒,M是线的“奇分点" (写出一种情况即可), 如果同时点从点A的位置开始以每秒2cm的速度向点B运动, 如图(3)所示, 井与点同时停止, 则当___________秒,M是线段AN的“奇分点”.
22.(2022·浙江舟山·七年级期末)已知点C在线段AB上,AC=2BC,点D、E在直线AB上,点D在点E的左侧,
(1)若AB=18,DE=8,线段DE在线段AB上移动,
①如图1,当E为BC中点时,求AD的长;
②当点C是线段DE的三等分点时,求AD的长;
若AB=2DE,线段DE在直线上移动,且满足关系式,则= .
22.(2022·浙江金华·七年级期末)如图,直线AB与EF相交于点O,∠AOE=60°,射线OC平分∠BOE.
(1)求∠COF的度数;
(2)将射线OC以每秒2°的速度绕点O顺时针旋转,同时直线EF以每秒6°的速度绕点O顺时针旋转,设运动时间为t秒(0<t≤60).
①当射线OE与射线OC重合时,求∠AOE的度数;
②旋转过程中,若直线EF平分∠BOC或平分∠AOC,求t的值.
一、选择题
1.(本题3分)(2022·浙江金华·七年级期末)下列图形中,线段能表示点P到直线l的距离的是( ).
A.B.C.D.
2.(本题3分)(2022·浙江舟山·七年级期末)下列四个图中,能用∠1、∠AOB、∠O三种方法表示同一个角的是( )
A.B.C.D.
3.(本题3分)(2020·浙江·七年级期末)点C在线段上,下列条件中不能确定点C是线段中点的是( )
A. B. C. D.
4.(本题3分)(2020·浙江·台州市路桥实验中学七年级阶段练习)如图,已知直线AB,CD相交于点O,OE平分∠COB,如果∠EOB=55°,那么∠BOD的度数是( )
A.35° B.55° C.70° D.110°
5.(本题3分)(2020·浙江宁波·七年级期末)一个角的余角比它的补角的一半少,则这个角的度数为( )
A. B. C. D.
6.(本题3分)(2020·浙江宁波·七年级期末)如图,点在线段上,且.点在线段上,且.为的中点,为的中点,且,则的长度为( )
A.15 B.16 C.17 D.18
7.(本题3分)(2019·浙江·颍上县教育局七年级课时练习)把用度、分、秒表示正确的是( )
A. B. C. D.
8.(本题3分)(2021·浙江湖州·七年级期末)若用如图①这样一副七巧板,拼成图②的图案,则图②中阴影部分的面积是空白部分面积的( )
A. B. C. D.
9.(本题3分)(2019·浙江·七年级阶段练习)如图,在线段上有、两点,长度为,长为整数,则以、、、为端点的所有线段长度和不可能为( )
A. B. C. D.
10.(本题3分)(2022·全国·七年级课时练习)如图,直线与相交于点,一直角三角尺的直角顶点与点重合,平分,现将三角尺以每秒的速度绕点顺时针旋转,同时直线也以每秒的速度绕点顺时针旋转,设运动时间为秒(),当平分时,的值为( )
A. B. C.或 D.或
二、填空题
11.(2021·湖北·公安县教学研究中心七年级期末)若的度数为,且与互余,则的度数为____.
12.(2021·吉林省第二实验高新学校七年级阶段练习)如图,经过刨平的木板上的两个点,能弹出一条笔直的墨线,而且只能弹出一条墨线,能解释这一实际应用的数学知识是 _____.
13.(2022·山东·日照市北京路中学七年级期中)如图,AB、CD相交于点O,OM平分∠BOD,∠MON是直角,,则∠DON的度数是__________.
14.(2022·浙江·宁波市海曙外国语学校七年级开学考试)点O为直线l上一点,射线OA、OB均与直线l重合,将射线OB绕点O逆时针旋转α(0≤α≤90°),过点O作射线OC、OD、OM、ON,使得∠BOC=90°,∠COD=2α,∠COM=∠AOC,∠CON=∠COD(OM在∠AOC内部,ON在∠COD内部),当∠MON=α时,则α=_____.
15.(2020·浙江杭州·模拟预测)如图,点是线段上一点,,若的长为,则的长为______.
16.(2020·浙江绍兴·七年级阶段练习)如图,点A、O、B都在直线MN上,射线OA绕点O按顺时针方向以每秒4°的速度旋转,同时射线OB绕点O按逆时针方向以每秒6°的速度旋转(当其中一条射线与直线MN叠合时,两条射线停止旋转).经过____________秒,∠AOB的大小恰好是60°.
三、解答题
17.(2020·浙江省义乌市稠江中学七年级阶段练习)如图:A,B,C是平面上三个点,按下列要求画出图形.
(1)作直线BC,射线AB,线段AC.
(2)小明认为从A到C的所有线中,线段AC最短,其数学依据是 .
18.(2022·浙江金华·七年级期末)如图,已知OB是内一条射线,OE平分,OF平分.
(1)若,,求的度数;
(2)试判断是否成立.并请说明理由.
19.(2021·浙江省衢州市衢江区实验中学七年级开学考试)如图,线段AC=10cm,点M是AC的中点,在CB上取一点N,使得CN︰NB=3︰4,若CN=,求MN的长.
20.(2022·浙江台州·七年级阶段练习)如图,直线CD,EF相交于点O,射线OA在∠COF的内部,∠DOF=∠AOD.
(1)如图1,若∠AOC=120°,求∠EOC的度数;
(2)如图2,若∠AOC=α(60°<α<180°),将射线OA绕点O逆时针旋转60°,到OB,
①求∠EOB的度数(用含α的式子表示);
②观察①中的结果,直接写出∠AOC,∠EOB之间的数量关系.
如图3 ,0°<∠AOC <120°,将射线OA绕点O顺时针旋转60°,到OB,请直接写出∠AOC,∠EOB之间的数量关系.
21.(2022·浙江宁波·七年级期末)如图(1).点在线段上.图中共有三条线段: 线段, 线段, 线段, 若其中有一条线段的长度是另一条线段长度的两掊, 则称点为线段的 “奇分点”.若, 如图(2), 点从点开始以每秒3cm的速度向A运动,当点M到达A点时停止运动,运动的时间为t秒.当t=_____________秒,M是线的“奇分点" (写出一种情况即可), 如果同时点从点A的位置开始以每秒2cm的速度向点B运动, 如图(3)所示, 井与点同时停止, 则当___________秒,M是线段AN的“奇分点”.
22.(2022·浙江舟山·七年级期末)已知点C在线段AB上,AC=2BC,点D、E在直线AB上,点D在点E的左侧,
(1)若AB=18,DE=8,线段DE在线段AB上移动,
①如图1,当E为BC中点时,求AD的长;
②当点C是线段DE的三等分点时,求AD的长;
若AB=2DE,线段DE在直线上移动,且满足关系式,则= .
22.(2022·浙江金华·七年级期末)如图,直线AB与EF相交于点O,∠AOE=60°,射线OC平分∠BOE.
(1)求∠COF的度数;
(2)将射线OC以每秒2°的速度绕点O顺时针旋转,同时直线EF以每秒6°的速度绕点O顺时针旋转,设运动时间为t秒(0<t≤60).
①当射线OE与射线OC重合时,求∠AOE的度数;
②旋转过程中,若直线EF平分∠BOC或平分∠AOC,求t的值.
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
